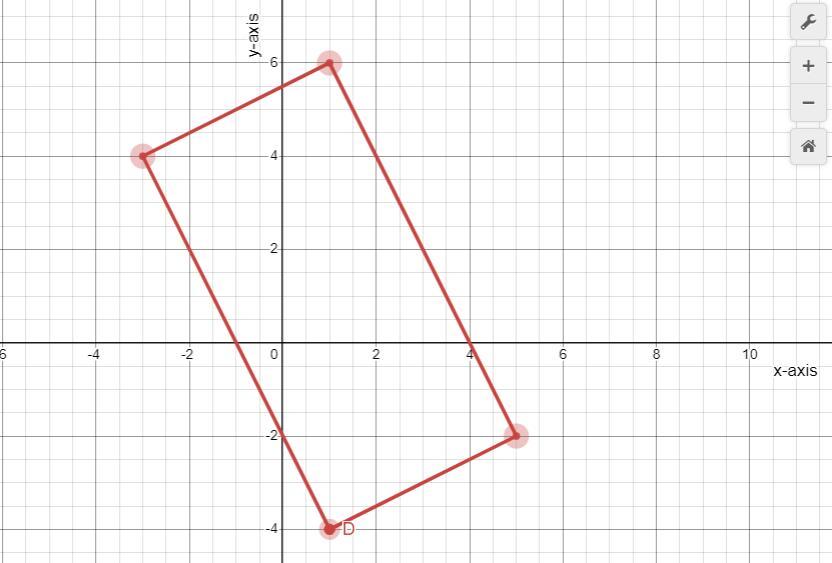
Plot the following points on graph paper and connect them in the order given.
Then connect points A and D.
A(-3, 4), B(1,6), C(5,-2), and D(1,-4)
If ABCD is rotated 90° clockwise (U) about the origin to form A'B'C'D', what
are the coordinates of the vertices of A'B'C'D'?

subtract 3 from both sides to get

4x > 27

divide both sides by 4 to get

x > 27/4 or 6 3/4

The probability is 35/1296, or approximately 0.027 or 2.7%.

What is the probability?

Probability is the study of the chances of occurrence of a result, which are obtained by the ratio between favorable cases and possible cases.

The total number of outcomes when rolling a pair of dice is 36 (since each die has 6 faces and can result in 6 possible outcomes).

To find the probability of the first roll resulting in a total of at least 3, we need to determine the favorable outcomes. The only combination that does not result in a total of at least 3 is when both dice show a 1, which is only one possible outcome. So, there are 35 favorable outcomes (36 total outcomes - 1 unfavorable outcome) for the first roll.

To find the probability of the second roll resulting in a total of at least 12, we need to determine the favorable outcomes. The only combination that results in a total of 12 is when both dice show a 6, which is only one possible outcome. So, there is only 1 favorable outcome for the second roll.

Therefore, the probability of the first roll resulting in a total of at least 3 and the second roll resulting in a total of at least 12 is:

(35/36) * (1/36) = 35/1296

Hence, the probability is 35/1296, or approximately 0.027 or 2.7%.

To learn more about probability, Visit

https://brainly.com/question/13604758

#SPJ1

The mean score is 628.

What is mean?

In statistics, the mean is a measure of central tendency, which represents the average value of a data set. It is also known as the arithmetic mean and is calculated by adding up all the values in the data set and then dividing by the number of observations in the data set. The formula for calculating the mean is:

mean = (sum of all values) / (number of observations)

Now,

To find the mean score, you need to add up the three scores and then divide by 3:

(650 + 600 + 635) / 3 = 628.33

Rounding to the nearest whole point, the mean score is 628.

To know more about Mean visit the link

brainly.com/question/30112112

#SPJ1

Therefore, the height of the right triangle is 9.6 units.

A triangle is a geometric figure that consists of three line segments that intersect at three endpoints, called vertices. The line segments are called sides, and the vertices where they intersect are called angles. A triangle can be classified based on the length of its sides and the measure of its angles. Triangles are fundamental to many areas of mathematics and physics, and they have a wide range of applications in real-life situations, such as in architecture, engineering, and surveying.

Here,

To find the height of a right triangle, we can use the formula:

h = (a * b) / c

where "a" and "b" are the lengths of the legs of the right triangle, and "c" is the length of the hypotenuse.

In this case, we have a right triangle with legs of lengths 12 units and 16 units, and a hypotenuse of length 20 units. Therefore, we can substitute these values into the formula and solve for the height:

h = (12 * 16) / 20

h = 192 / 20

h = 9.6

To know more about triangle,

https://brainly.com/question/28600396

#SPJ1

As a result, the square's sides measure about **6.08 cm** in length.

The following formula is used to determine a square's area:

Area = side² is a formula.

where "side" denotes the measurement of one of the square's sides.

Assume for the moment that the two squares have sides that are 'x' and 'y' long. We are aware that a square's area is equal to the square of one of its sides. Consequently, using the above data, we can create the following two equations:

``` x² + y² = 74   (Equation 1)

The second equation is x = y.

Equation 2 can be entered in place of Equation 1 to yield:

2x² = 74,

x² = 37, and

x = √(37)

= 6.08, respectively.

To know more about side of square visit:

brainly.com/question/24584437

#SPJ1

the employer's total FUTA and SUTA tax is: $2,928

What is tax rate?

The percentage of income that a person or corporation must pay or withhold as taxes is known as the effective tax rate.

$7,000 (for Zachary Fox) + $7,000 (for Calvin Bell) + $7,000 (for David Alexander) + $7,000 (for Michael Sierra) = $28,000

The FUTA tax for this amount is:

$28,000 × 6.0% = $1,680

Therefore, the total taxable earnings subject to SUTA tax is:

$26,000 (for each employee) × 4 (number of employees) = $104,000

The SUTA tax for this amount is:

$104,000 × 1.2% = $1,248

The year-to-date FUTA and SUTA taxes are not given explicitly, so we cannot calculate the current period FUTA and SUTA taxes.

Therefore, the employer's total FUTA and SUTA tax is:

$1,680 (FUTA tax) + $1,248 (SUTA tax) = $2,928

To know more about tax rate visit,

https://brainly.com/question/29800484

#SPJ1

Answer:

A = 50.24 m²

Step-by-step explanation:

A = π r²

d = 8 m

r = d/2

r = 8/2

r = 4 m

A = 3.14 × (4)² m

A = 3.14 × 16 m

A = 50.24 m²

Answer:

50.24 m²

Step-by-step explanation:

Diameter = 8 m

Formula

Radius ( r ) = Diameter/2

r = 8/2

r = 4 m

Formula

Area of circle = π r²

Note

The value of π is 3.14 ( approximately )

Area of circle

= 3.14 × 4²

= 3.14 × 4 × 4

= 3.14 × 16

= 50.24 m²

Hence,

The area of circle is 50.24 m².

The limit of the income of middle 50% of the families is 578.125 - 1850.

In mathematics, the concept of a "limit of income" is not a standard mathematical term or concept. The idea of a limit is typically used in calculus to describe the behavior of functions as their inputs approach certain values.

A limit is the value that a function approaches as its input approaches a certain value. For example, if a function approaches a certain value as x gets closer and closer to a certain number, we say that the limit of the function as x approaches that number is the value it approaches.

However, in the context of income, the term "limit of income" could potentially be used to refer to certain mathematical concepts, such as:

Marginal tax rate: This is the tax rate that applies to an additional unit of income earned. As income increases, the marginal tax rate may increase, leading to a "limit" on the amount of after-tax income that can be earned.

Maximum allowable contribution: Some retirement savings plans, such as IRAs or 401(k)s, may have limits on the maximum amount of contributions that can be made each year. This could be considered a "limit of income" in the sense that it restricts the amount of income that can be saved in these accounts.

First it should be in proper order,

⇒ 0-500. 50. 50

⇒ 500-1000. 80. 130

⇒ 1000-1500. 40. 170

⇒ 1500-2000. 25. 195

⇒ 2000-2500. 25. 220

⇒ 2500-3000. 15. 235

⇒ 3000-3500. 10. 245

⇒ 3500-4000 5. 250

∴ We have to find the limits of middle 50% of the families

Q1 ------------- Q3

25%. 50% 75%, middle50% will have their income between Q3 and Q1

Q1 = N÷4 th item = 250÷ 4= 62.5th item ,it lies in the class interval 500-1000

62.5 -50

Q1 = 500 + ------------- ×. 500

80

Q1 = 500+ 78.125 = 578.125

Q3 = 3N ÷ 4 = 3(250) ÷ 4 = 187.5 th item ,it lies in class interval 1500-2000

187.5-170

Q3 = 1500 + ------------ × 500

25

Q3 = 1500 + 350 = 1850 so , limits of middle 50% families = 578.125 - 1850

To know more about limit of income visit:

https://brainly.com/question/31054850

#SPJ1

Answer:

The area of the shape is 56 to the nearest tenth

Step-by-step explanation:

r=d/2

d=2r

d=2×3=6

Area of shape=Area of rectangle+Area of semi circle

A=L×B+1/2pir²

A=7×6+1/2×22/7×3²

A=42+11/7×9

A=42+99/7

A=42+14.14

A=56.14

A=56 to the nearest tenth

The value of x from the given figure is given as follows:

144º.

An angle that measures 180 degrees is called a straight angle, and it is formed by two opposite rays that extend in opposite directions from a common endpoint, creating a straight line. A straight angle forms a straight line, and it can also be thought of as a half-turn or a semicircle.

The two opposite rays in this problem have the measures given as follows:

Hence the equation to find the value of x is given as follows:

x + x/4 = 180

x + 0.25x = 180

1.25x = 180

x = 180/1.25

x = 144º.

More can be learned about straight angles at https://brainly.com/question/24024505

#SPJ1

Equations with a single unknown can be powerful tools in helping us understand complex phenomena and make predictions about how they will behave.

Yes, equations with a single unknown can be very helpful in understanding various phenomena. Mathematical equations allow us to express relationships between different variables and make predictions about how they will behave under different conditions. By solving equations, we can find the values of unknown variables and gain a deeper understanding of the system we are studying.

Other examples of equations with a single unknown that have had a significant impact include Newton's second law of motion, F=ma, which relates force (F) to mass (m) and acceleration (a), and the ideal gas law, PV=nRT, which relates pressure (P), volume (V), number of moles (n), and temperature (T) of a gas.

equations with a single unknown can be powerful tools in helping us understand complex phenomena and make predictions about how they will behave.

To know more about complex visit:

https://brainly.com/question/29377605

#SPJ1

Assuming it's breadth is 4 1/2 m.

Assuming it's length is 8 1/4 m.

Assuming it's height is 6 1/2 m

Then the volume of a rectangular prism is given as l x b x h. Which means we multiply all the sides by one another. From my assumption of values, we have that 8 1/4 x 4 1/2 x 6 1/2, and this gives us 241.3125 m³ or 241.31

The equation of p(x) in vertex form is;

p(x) = 9.67(x + 1.04)² - 10.25

The closest answer choice is:

p(x) = 3(x - 1)²  - 2, which is not correct.

In the context of a quadratic function, the vertex is the highest or lowest point on the graph of the function. It is the point where the parabola changes direction. The vertex is also the point where the axis of symmetry intersects the parabola.

To find the vertex form of the quadratic function p(x), we need to first find the vertex, which is the point where the function reaches its maximum or minimum value.

To find the vertex, we can use the formula:

x = -b/2a, where a is the coefficient of the x²  term, b is the coefficient of the x term, and c is the constant term.

Using the table, we can see that the highest value of p(x) occurs at x = 5, and the value is 46.

We can then use the formula to find the vertex:

x = -b/2a = -5/2a

Using the values from the table, we can set up two equations:

46 = a(5)² + b(5) + c

1 = a(0)²  + b(0) + c

Simplifying the second equation, we get:

1 = c

Substituting c = 1 into the first equation and solving for a and b, we get:

46 = 25a + 5b + 1

-20 = 5a + b

Solving for b, we get:

b = -20 - 5a

Substituting b = -20 - 5a into the first equation and solving for a, we get:

46 = 25a + 5(-20 - 5a) + 1

46 = 15a - 99

145 = 15a

a = 9.67

Substituting a = 9.67 and c = 1 into b = -20 - 5a, we get:

b = -20 - 5(9.67) = -71.35

Therefore, the equation of p(x) in vertex form is:

p(x) = 9.67(x - 5)²  + 1

Simplifying, we get:

p(x) = 9.67(x²  - 10x + 25) + 1

p(x) = 9.67x²  - 96.7x + 250.85 + 1

p(x) = 9.67x²  - 96.7x + 251.85

Rounding to the nearest hundredth, we get:

p(x) = 9.67(x - 5²  + 1 = 9.67(x + 1.04)²  - 10.25

Therefore, the answer is:

p(x) = 9.67(x + 1.04)² - 10.25

The closest answer choice is:

p(x) = 3(x - 1)²  - 2, which is not correct.

To know more about vertex visit:

https://brainly.com/question/29476657

#SPJ1

The probability that a person who tests positive actually has the disease is ≈0.0158.

        Probability is a way to gauge how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about the likelihood of an event happening, or how likely it is. Probability can range from 0 to 1, with 0 denoting an impossibility and 1 denoting a certainty. 1 is the probability of every event in a sample space.

    For instance, when we flip a coin, there are just two possible results: Head OR Tail. (H, T). However, if two coins are tossed, there are four possible results: (H, H), (H, T), (T, H), and (T, T).

we solve the given question using BAYE's theorem:

Bayes' Theorem states that the conditional probability of an event, based on the occurrence of another event, is equal to the likelihood of the second event given the first event multiplied by the probability of the first event.

P(disease/positive)= [tex]\frac{P(disease)P(positive/disease)}{P(disease)P(positive/disease)+P(no disease)P(positive/disease)}[/tex]

P(disease/positive)= [tex]\frac{(0.008)(0.04)}{(0.008)(0.04)+(0.992)(0.02)}[/tex]  ≈ 0.0158

To know more about Bayes' Theorem visit:

brainly.com/question/29598596

#SPJ1

The statements that are always true regarding the given diagram of the triangle are m∠2 + m∠3 = m∠6, m∠3 + m∠4 + m∠5 = 180°, m∠5 + m∠6 = 180°. Therefore, options (4) and (5) are not always true.

An exterior angle of a polygon is an angle that forms a linear pair with an interior angle of the polygon. In other words, it is an angle formed by extending one of the sides of the polygon. For any given vertex of the polygon, the exterior angle is the angle between a line containing the side of the polygon next to the vertex and a line that is an extension of the adjacent side. The measure of an exterior angle is equal to the sum of the measures of its corresponding remote interior angles (interior angles that are not adjacent to the exterior angle). The sum of the exterior angles of any polygon, including a triangle, is always equal to 360 degrees. Exterior angles are used in a variety of geometric proofs and constructions.

We know that the sum of all the interior angles of any triangle is 180 degrees. Therefore, we can use this fact to determine which statements are always true regarding the given diagram.

Now, we can use the following relationships between the interior and exterior angles of a triangle:

Exterior angle = Sum of interior angles adjacent to it

Interior angle = 180  - Exterior angle

Using these relationships, we can determine which statements are always true:

m∠5 + m∠3 = m∠4: This is true because the exterior angle at angle 3 is equal to the sum of angles 3 and 4, and the exterior angle at angle 5 is equal to the sum of angles 5 and 6. Therefore, m∠5 + m∠3 + m∠6 = m∠4 + m∠3, which simplifies to m∠5 + m∠3 = m∠4.

Given m∠3 + m∠4 + m∠5 = 180°: This is true because the sum of all the interior angles of a triangle is 180 degrees.

m∠5 + m∠6 = 180°: This is not always true because sum of all the angles should be 180. It is true in this specific case because angle 1 is a straight angle, which means that m∠5 + m∠6 = 180°. However, in general, this statement is not always true.

m∠2 + m∠3 = m∠6: This is true because the exterior angle at angle 2 is equal to the sum of angles 2 and 6. Therefore, m∠2 + m∠3 = m∠6.

Given m∠2 + m∠3 + m∠5 = 180°: This is may not always true. It is true in this specific case because angle 1 is a straight angle, which means that m∠2 + m∠3 + m∠5 = 180°. However, in general, this statement is not always true.

Therefore, the three statements that are always true from the diagram are:

m∠5 + m∠3 = m∠4

m∠3 + m∠4 + m∠5 = 180°

m∠2 + m∠3 = m∠6

To know more about exterior angles visit:

brainly.com/question/28835566

#SPJ1

Answer:

A) $2510

B) $209.17

C) $128,273.36

Step-by-step explanation:

Let's break this problem down into three parts:

a) To find out how much will be saved each year, we first need to calculate the annual salary and then determine 10% of it. Since the newscaster earns $25,100, we can calculate the annual savings as follows:

Annual savings = Annual salary * 10%

Annual savings = $25,100 * 0.1

Annual savings = $2,510

So, the newscaster will save $2,510 each year.

b) To find the monthly deposit, we need to divide the annual savings by the number of months in a year:

Monthly deposit = Annual savings / 12

Monthly deposit = $2,510 / 12

Monthly deposit ≈ $209.17

The newscaster will deposit approximately $209.17 per month into the retirement account.

c) To find the amount in the account after 29 years, we will use the formula for the future value of an ordinary annuity, since the investment has a monthly deposit and a monthly compounding interest rate:

FV = P * [(1 + r)^nt - 1] / r

Where FV is the future value, P is the monthly deposit, r is the monthly interest rate (annual interest rate divided by 12), n is the number of times interest is compounded per year (monthly, so 12), and t is the number of years.

In this case, P = $209.17, r = 4.1%/12, n = 12, and t = 29 years.

First, convert the annual interest rate to a decimal and then find the monthly interest rate:

Monthly interest rate = (4.1%/12) / 100

Monthly interest rate = (0.041/12)

Now, plug the values into the formula:

FV = $209.17 * [(1 + 0.041/12)^(12*29) - 1] / (0.041/12)

Calculate the future value:

FV ≈ $209.17 * [(1.003417)^(348) - 1] / (0.003417)

FV ≈ $209.17 * (3.42307) / (0.003417)

FV ≈ $128,273.36

After 29 years, the newscaster will have approximately $128,273.36 in the retirement account.

The measures of the arcs on the circle are;

mPQ = 71°

mSR = 161°

mQRT = 119°

mPSR = 270°

mPS = 109°

An arc is a part of the circumference of a circle.

The vertical angles theorem indicates that we get;

m∠QUR = m∠TUS = 19°

∠PUQ and ∠QUR are complementary angles (Specified angle of ∠PUR)

∠PUQ + ∠QUR = 90°

m∠PUQ = 90° - m∠QUR

m∠PUQ = 90° - 19° = 71°

The measure of arcPQ = m∠PUQ = 71°

Therefore, mPQ = 71°

∠SUR and ∠QUR are supplementary angles (Definition of linear pair angles)

Therefore; m∠SUR + m∠QUR = 180°

m∠SUR  = 180° - 19° = 161°

mSR = m∠SUR = 161°

mQRT = m∠QUS + m∠TUS

m∠QUS = 180°, therefore;

mQRT = 180° + 19° = 199°

mQRT = 199°

mPSR = 360° - m∠PUR (Sum of angle at the the center of a circle)

mPSR = 360° - 90° = 270°

mPS = m∠TUS + m∠PUT

m∠PUT and m∠PUR are linear pair angles,m∠PUR = 90°, therefore;

m∠PUT = 90°

mPS = 19° + 90° = 109°

Learn more on vertical angles here: https://brainly.com/question/24272583

#SPJ1

Based on the information given, we can use the Pythagorean theorem to determine the distance traveled by the northbound car.

Let's denote the distance traveled by the northbound car as 'x' kilometers.

According to the Pythagorean theorem, in a right triangle, the square of the hypotenuse (the straight-line distance between the two cars) is equal to the sum of the squares of the other two sides (the distances traveled by each car).

In this case, the northbound car's distance is 'x' kilometers and the eastbound car's distance is 5 kilometers.

So we have the equation:

x^2 + 5^2 = 13^2

Simplifying, we get:

x^2 + 25 = 169

Subtracting 25 from both sides, we get:

x^2 = 144

Taking the square root of both sides, we get:

x = 12

So the northbound car has traveled 12 kilometers.

Answer: 12 km

Step-by-step explanation:

As seen in the figure the distance that the northbound car traveled equals to the distance from point N to the parking lot.

pythagorean: [tex]\sqrt{13^{2}-5^{2} }=12km[/tex]

We can prove that if there exists a walk of odd length starting and ending at vertex v in a graph G, then there must exist an odd cycle that does not repeat any vertices.

what is  vertex ?

In mathematics, a vertex is a point where two or more lines, curves, or edges meet. It is a common term used in geometry, graph theory, and other areas of mathematics.

In the given question,

We can prove that if there exists a walk of odd length starting and ending at vertex v in a graph G, then there must exist an odd cycle that does not repeat any vertices.

To see why, suppose there exists a walk w of odd length starting and ending at v, and suppose w is the shortest such walk. If w does not repeat any vertices, then we have found an odd cycle that does not repeat any vertices, and we are done.

Suppose instead that w repeats some vertex v' (not equal to v). Then we can split w into two walks, w1 and w2, where w1 starts at v, goes to v', and then returns to v, and w2 is the rest of w starting and ending at v'. Since v' is not equal to v, both w1 and w2 are walks of odd length, and both are strictly shorter than w. By the minimality of w, both w1 and w2 must contain odd cycles that do not repeat any vertices. We can then combine these cycles to form an odd cycle that does not repeat any vertices in G, and we are done.

To know more about  vertex , visit:

https://brainly.com/question/30940247

#SPJ1

Answer:

The train pulled by teeth is 1.45 metric tons heavier or 1 9/20 metric tons heavier than the train pulled with a beard.

Step-by-step explanation:

Least Common Denominator (LCD): 20

2 3/4 metric tons = 2 15/20 = 2.75 metric tons

4 1/5 metric tons = 4 4/20 = 4.2 metric tons

FRACTION:

4 4/20 = 84/20

2 15/20 = 55/20

DECIMAL:

4.20-2.75 = 1.45 metric tons

Difference In Weight: (84-55)/20 = 29/20 = 1 9/20 = 1.45 metric tons

4.2/2.75 = 52.727273% heavier

HOPE THIS HELPS!!!

Thus, the time taken for the sum of $1500 to become $1600 with 6.49% simple annual interest rate is found as 1.027 years.

Simple interest is the percentage that is charged on the principal sum of money that is lent or borrowed. Similar to this, when you deposit a particular amount in a bank, you can also earn interest.

Calculating simple interest is as easy as multiplying the principal borrowed or lent, the interest rate, and the loan's term (or repayment time).

Given data:

Principal P = $1500

Amount after interest A = $1600

Rate of simple interest R = 6.49%

Time  = T years

The formula for the simple interest:

SI = PRT/100

A = P + SI

A = P + PRT/100

PRT/100 = A - P

1500*6.49*T/100 = 1600 - 1500

1500*6.49*T = 100 *100

T = 10000 / 9735

T = 1.027 years

Thus, the time taken for the sum of $1500 to become $1600 with 6.49% simple annual interest rate is found as 1.027 years.

Know more about the simple interest:

https://brainly.com/question/25793394

#SPJ1

As a result, the cylinder's volume is roughly **5541.48 mm³**.

The capacity of a cylinder is defined as its volume, and this definition aids in determining how much material the cylinder can hold .The volume of a cylinder—which corresponds to how much material can be transported inside of it or immersed in it—determines its density.. The formula r²πh, where r is the radius of the circular base and h is the height of the cylinder, determines the volume of a cylinder.

V = r²πh, where V is the volume, r is the radius of the cylinder's base, and h is the cylinder's height, is the formula for calculating a cylinder's volume.

When we enter the specified values into the formula, we obtain:

V = π(14)²(9)

V = 1764π

Rounding to the closest hundredth using 3.14, we obtain:

V ≈ 5541.48 mm³

To know more about volume of cylinder visit:

brainly.com/question/16788902

#SPJ1

If each person drove at a constant rate,than Laura drove the fastest

Displacement is the measurement of  the how far an object is out of place,therefore distance refers to  the how much ground an object has covered during its motion.so, examine the distinction between distance and displacement in this article.

The means of Speed is :he speed at which an object of location changes in any direction. The distance traveled in relation to the time it took to travel that distance is how speed is defined. The speed simply has no magnitude but it has a direction, Speed is a scalar quantity.

to compute who drove the quickest by Using this   formula

speed=Distance /time,

first of all the convert times into hours:

Hank: 3.2 hours x 3 hours and 12 minutes.

Laura: 2.5 hours is 2 hours and 30 minutes.

Nathan: 2.25 hours is 2 hours and 15 minutes.

Raquel: 4 hours plus 24 minutes equals 4.4 hours.

now to calculate the speed by above formula

Hank: 55 miles per hour for 176 miles in 3.2 hours.

Laura: 60 miles per hour equals 150 miles in 2.5 hours.

Nathan: 50 miles per houris equal to 112.5 miles in 2.25 hours.

Raquel: 65 miles for 286 miles in 4.4 hours.

As a result, Laura moved the fastest, clocking in at 60 miles. The solution, Laura, is B.

Learn more about speed here:

https://brainly.com/question/31273613

#SPJ1

Answer: you need to add

Step-by-step explanation: I would ask your teacher to help you understand the lesson.  

Hence,we only have a sample of the population, we can never be entirely certain of the true value of p.

A  population in statistics is a group of comparable  objects or occurrences that  are relevant to a  particular topic or experiment.  A statistical population can  be a collection of real things or  a hypothetical, possibly limitless collection  of objects derived from experience.

You need two  numbers to  complete it.  One  is the   sample size (n),  while the  other is the quantity (X) of instances of the relevant event  or  parameter.  P-hat is  described by the  equation p-hat = X/n.   To put it another way:  You calculate p-hat by dividing the quantity of the desired event by the sample size.

p-hat stands for the sample population , which is 73% or 0.73.

We can't immediately calculate the standard error of the sample proportion because we don't know the population's size or the sample size. When the sample size is sufficient, we can use the normal approximation to the binomial distribution, which is valid.

The standard error of the sample proportion is calculated as follows, assuming that the normal approximation holds true:

[tex]SE =\sqrt{(p-hat * (1 - p-hat)/n)}[/tex]

where the sample size is n.

We can not  immediately compute SE because we do not know n. However, by assuming that p-hat equals 0.5 (i.e., the least certain value for p-hat), we can adopt a cautious estimate of the standard error. than we get

[tex]SE = \sqrt{(0.5*(1-0.5)/n)} = 0.5/\sqrt{n}.[/tex]

We can use the formula: to create a 95% confidence interval for p.

p=p-hat ± 1.96 * SE

where 1.96 is the z-score at a 95% confidence level.

In place of the values we hold:

[tex]\sqrt{n}[/tex]= 1.96 * 0.5 / p-hat

We are looking for a range  of values that, with a 95% level of confidence,  are likely to contain  the value p because we want to  anticipate it. When we solve for p, we get:

p = p-hat ± 1.96 * SE

p = 0.73 ± 1.96 * 0.5 /[tex]\sqrt{n}[/tex]

we are unable  to determine a specific  range of values for p since we  do not know n. To show  how the range of values  for p changes, we can use a variety of sample sizes.

Consider the case where the sample size is 100. Then:

p = 0.73 ± 1.96 * 0.5 /[tex]\sqrt{100}[/tex]

p = 0.73 ± 0.098

therefore, we  now have a 95% confidence  range for p is (0.632, 0.828).

If the sample  size is increased to 1,000, then:

p = 0.73 ± 1.96 * 0.5 /[tex]\sqrt{1000}[/tex]

p = 0.73 ± 0.031

therefore we  now have a 95% confidence range for p of roughly (0.699, 0.761).

As we can  see, as the  sample size grows, the range of values for p becomes less. Since we only have a sample of the population, we can never be entirely certain of the true value of p.

Learn more about sample size here:

https://brainly.com/question/21698404

#SPJ1.

If the area of a rectangle is 1 1/2 square feet and the width of the rectangle is 3/5 feet then the length of the rectangle is  5/2 square feet.

We can use the formula for the area of a rectangle, which is: Area = (length x width) We know that the area of the rectangle is 3/2 square feet, and we also know that the width of the rectangle is 3/5 feet. So we can plug in these values and solve for the length:3/2 sq. ft. = length x 3/5 ft.

To solve for the length, we can start by multiplying both sides of the equation by the reciprocal of  1 1/2 =3/5:

(3/2 sq. ft.) / (3/5 ft.) = length

(3/2 sq. ft.) x (5/3 ft.) = length

(3 x 5) / (2 x 3) sq. ft. = length

15/6 sq. ft. = length

5/2 sq. ft. = length

Therefore, the length of the rectangle is 5/2 square feet.

Learn more about rectangle at:

https://brainly.com/question/11537961

#SPJ1

Therefore, the correct response From these integral is option D   is.  

``` 10 + ∫₅¹  R(t) dt

An integral is a mathematical construct in mathematics that can be used to represent an area or a generalization of an area. It computes volumes, areas, and their generalizations. Computing an integral is the process of integration.

Integration can be used, for instance, to determine the area under a curve connecting two points on a graph. The integral of the rate function R(t) with respect to time t can be used to describe how much water is present in a tank.

The following equation can be used to determine how much water is in the tank at time t = 5 if there are 10 gallons of water in the tank at time t = 1.

``` 10 + ∫₅¹  R(t) dt

To know more about integral visit:

brainly.com/question/30900582

#SPJ1