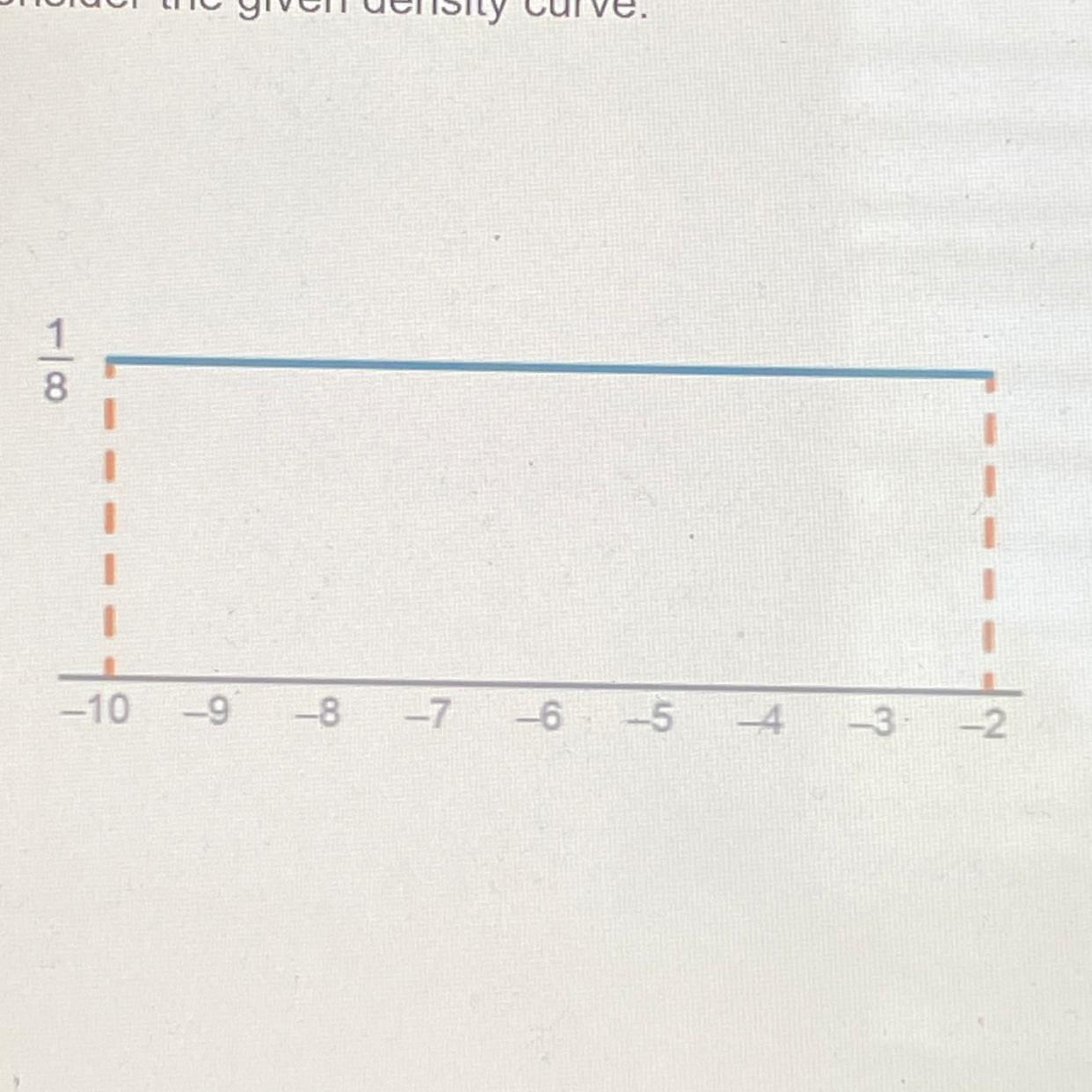
Consider the given density curve.


What is the value of the median?
O-10
O-7
O-6
O-2

The relation that is a function is D: {(–3, 2), (–2, 3), (–1, 2), (0, 4), (1, 1)}.

A function is a relation between a set of inputs and a set of possible outputs with the property that each input is related to exactly one output. In other words, for a relation to be a function, each input can only be related to one output.

In relation D, each input (x-value) has a unique output (y-value), meaning that each x-value is only paired with one y-value. In contrast, relations A, B, and C have repeated x-values with different y-values, which means that they are not functions.

In relation A, the input -1 is paired with two different outputs (2 and 3). In relation B, both inputs 0 and -1 are each paired with two different outputs. In relation C, both inputs 0 and -3 are each paired with two different outputs. Therefore, only relation D satisfies the definition of a function.

More on relation can be found here: https://brainly.com/question/18790700

#SPJ1

Candy accounts for 15% of the total purchases, snacks account for 25%, automotive supplies account for 20%, and beverages account for 40%.

The correct circle graph representing the data in the table is:

circle graph titled convenience store purchases, with four sections labeled candy 15 percent, snacks 25 percent, auto supplies 20 percent, and beverages 40 percent.

This graph accurately represents the proportion of each item's purchases out of the total number of purchases. Candy accounts for 15% of the total purchases, snacks account for 25%, automotive supplies account for 20%, and beverages account for 40%.

to know more about circle

brainly.com/question/29142813

#SPJ1

We are adjusting the original rectangular solid and here is what we have:

(a) The lateral area is the sum of the areas of the four sides, which are all rectangles. The two sides with dimensions 8 x 3 have an area of 8 x 3 = 24 square units each, and the two sides with dimensions 10 x 3 have an area of 10 x 3 = 30 square units each. Therefore, the lateral area is:

2(24) + 2(30) = 48 + 60 = 108 square units

(b) The total area is the sum of the areas of all six faces. The two faces with dimensions 10 x 8 have an area of 10 x 8 = 80 square units each, the two faces with dimensions 8 x 3 have an area of 8 x 3 = 24 square units each, and the two faces with dimensions 10 x 3 have an area of 10 x 3 = 30 square units each. Therefore, the total area is:

2(80) + 2(24) + 2(30) = 160 + 48 + 60 = 268 square units

(c) The volume is the product of the length, width, and height of the rectangular solid. Therefore, the volume is:

10 x 8 x 3 = 240 cubic units

Learn more about rectangular solid here:

https://brainly.com/question/28123312

#SPJ1

We need to select at least 754 people for the experiment to estimate the fraction of people who black out at G forces greater than 6 with an error of at most 0.03 and a 95% confidence level.

We can use the formula for the sample size required to estimate a population proportion with a specified margin of error and confidence level:

n = (Z^2 * p * (1-p)) / E^2

where:

Z = the z-score corresponding to the desired confidence level (95% confidence level corresponds to a z-score of 1.96)

p = the estimated population proportion from the earlier study

E = the desired margin of error

Substituting the given values, we get:

n = (1.96^2 * 0.33 * (1-0.33)) / 0.03^2

n = 753.69

Rounding up to the next integer, we need a sample size of 754. Therefore, we need to select at least 754 people for the experiment to estimate the fraction of people who black out at G forces greater than 6 with an error of at most 0.03 and a 95% confidence level.

Learn more about sample size at  https://brainly.com/question/30123000

#SPJ1

Answer:

f(x) - g(x) = 2x² + 6x - 4

Step-by-step explanation:

f(x) - g(x)

= 3x² + x - 3 - (x² - 5x + 1) ← distribute parenthesis by - 1

= 3x² + x - 3 - x² + 5x - 1 ← collect like terms

= 2x² + 6x - 4

Answer:

2.5cm

Step-by-step explanation:

you half the diameter to get the radius

Rounding to the nearest hundredth, the total area is 238.64 square feet. Therefore, the correct answer is:

Area of circle: 50.24

Area of semicircles: 125.60

Area of quarter-circles: 251.20

Total area of pattern: 238.64

The area of a circle with radius 4 feet is:

Area of circle = π × [tex]r^{2}[/tex] = 3.14 × [tex]4^{2}[/tex] = 50.24 square feet

The area of a semicircle with radius 4 feet is half the area of a circle with the same radius:

Area of semicircle = 0.5 × Area of circle = 0.5 × 50.24 = 25.12 square feet

The area of a quarter-circle with radius 4 feet is a quarter of the area of a circle with the same radius:

Area of quarter-circle = 0.25 × Area of circle = 0.25 × 50.24 = 12.56 square feet

Flo bought 2 circular windows with an area of 50.24 × 2 = 100.48 square feet.

She also bought 5 semicircular windows with an area of 25.12 × 5 = 125.60 square feet.

And she bought 20 quarter-circular windows with an area of 12.56 × 20 = 251.20 square feet.

The total area of the windows purchased by Flo is:

Total area = 100.48 + 125.60 + 251.20 = 477.28 square feet.

Rounding to the nearest hundredth, the total area is 238.64 square feet. Therefore, the correct answer is:

Area of circle: 50.24

Area of semicircles: 125.60

Area of quarter-circles: 251.20

Total area of pattern: 238.64

to know more about circle

brainly.com/question/29142813

#SPJ1

Step-by-step explanation:

data given

men 330 ,days30

men? ,days11

from

men(m) are inversely proportional todays (d)

m=k/d

330×30=k

k=9900

now,

m=9900/11m

m=900

data given

friends 20, time 2hours

friends 30, time?

from

friends (f) are inversely proportional to time (t)

f=k/t

k=20×2

k=40

now,

t=40/30

t=1.3(1:18)

The two possible locations for the fourth vertex are (4, -4) and (-3, -1).

What is quadratic equation?

it's a second-degree quadratic equation which is an algebraic equation in x. Ax2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term, is the quadratic equation in its standard form.

To find the location of the fourth vertex of the square, we need to use the fact that a square has four equal sides and four right angles.

The first two vertices given are (4, 3) and (-3, 3), which lie on a horizontal line segment of length 7.

The third vertex is (-3, -4), which is 7 units away from the first two vertices and lies on a vertical line segment.

Since the square has four equal sides, the distance between the third vertex and the fourth vertex must also be 7 units.

And since the square has four right angles, the fourth vertex must be located on a vertical line passing through the first two vertices or on a horizontal line passing through the third vertex.

So, there are two possible locations for the fourth vertex:

(4, -4): This point is located 7 units below the first vertex (4, 3) on the vertical line passing through it.

(-3, -1): This point is located 7 units to the right of the third vertex (-3, -4) on the horizontal line passing through it.

Therefore, the two possible locations for the fourth vertex are (4, -4) and (-3, -1).

To learn more about quadratic equations from the given link:

brainly.com/question/30098550

#SPJ1

Using the formula for the area of a rectangle, the area of the cellphone is 18x⁻¹y⁸ OR 18y⁸/x

From the question, we are to calculate the area of the cellphone shown in the diagram

From the given information,

We have a diagram that shows a cellphone which is rectangular in shape.

Thus,

We will use the formula for finding the area of a rectangle to calculate the area of the cellphone.

Area of a rectangle = Length * Width

From the given information,

Length of the cellphone = 6x²y⁶

Width of the cellphone = 3x⁻³y²

Thus,

Area of the cellphone = 6x²y⁶ × 3x⁻³y²

Area of the cellphone = 6 × 3 × x² × x⁻³ × y⁶ × y²

Area of the cellphone = 18 × x⁻¹ × y⁸

Area of the cellphone = 18x⁻¹y⁸ OR 18y⁸/x

Hence,

The area of the cellphone is 18x⁻¹y⁸ OR 18y⁸/x

Learn more on Calculating area here: https://brainly.com/question/25292087

#SPJ1

Angle KRL is equal to 34°. The main reason behind this is that KRL is vertically opposite to Angle QRP.

KLR and LRM are complementary angles i.e.

KLR + LRM = 90

Similarly, HRQ and QRP are complementary angles i.e.

HRQ + QRP = 90

HRQ = 56 = LRM (vertically opposite angle)

KLR = KRM - LRM = 90 - 56 = 34

KLR = QRP = 34.

The two geometrical rules applied are,

(a) Vertically Opposite angles are always equal.

(b) Complementary angles are those angles which adds upto make 90 degree angle

To know more about Geometrical Rules, visit:

https://brainly.com/question/30430831

#SPJ1

The prompt that examines linear functions and ordered pairs are given below.

1) Here are the ordered pairs for each point:

Point A: (4, 9)

Point B: (6, 3)

Point C: (1, 3)

Point D: (8, 7)

Point E: (8, 9)

See the attached graph.

2) Part A: The completed table and graph for Derek is given as attached.

Part B: Derek makes 10 bracelets in 5 hours.

3) The ordered pairs are given in the labelled graph accordingly.

4) Deanna's coordinates plane is labelled and attached accordingly. The correct answer is Option B (5,8)

5) The other ordered pairs that could be the vertext are Options A - E. See the attached image (Miguel's Squre

Learn more about ordered pairs at:

https://brainly.com/question/30805001

#SPJ1

The statement "About 16% of the students scored 74 or below" is true for the given normal distribution of test scores with an average of 78 and a standard deviation of 4.

Standard deviation is a measure of the amount of variation or dispersion of a set of values from their mean (average) value. It is calculated as the square root of the variance of a set of data. A smaller standard deviation indicates that the values are tightly clustered around the mean, while a larger standard deviation indicates that the values are more spread out.

In the given question,

About 16% of the students scored 74 or below is true. This is because of the empirical rule for normal distributions, which states that approximately 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations. So, if the average score is 78 and the standard deviation is 4, a score of 74 falls one standard deviation below the mean, which represents about 16% of the total data.

To know more about standard deviation, visit:

https://brainly.com/question/23992131

#SPJ1

Answer:

About 97.5%  of the students scored 86 or below.

Step-by-step explanation:

Michelle can make 6 floor boards for her car.

To determine how many floor boards Michelle can make, we need to divide the total length of wood she has (13.2 meters) by the length of each floor board (2.2 meters).

The number of floor which boards Michelle can make is:

= 13.2 meters / 2.2 meters/floor board

= 6 floor boards

Therefore, Michelle can make 6 floor boards for her car using the 13.2 meters of wood she has.

Read more about floor board

brainly.com/question/25676992

#SPJ1

Answer: There are a total of 6 x 6 = 36 possible outcomes when rolling a pair of dice. We can count the number of outcomes where the sum of the dice is odd or a multiple of 3.

For the sum to be odd, we can have:

A 1 on one die and an even number on the other, or

A 3 on one die and an even number on the other, or

A 5 on one die and an even number on the other, or

A 2 on one die and an odd number on the other, or

A 4 on one die and an odd number on the other, or

A 6 on one die and an odd number on the other.

There are a total of 18 outcomes that satisfy this condition.

For the sum to be a multiple of 3, we can have:

A 1 on one die and a 2 on the other, or

A 1 on one die and a 5 on the other, or

A 2 on one die and a 1 on the other, or

A 2 on one die and a 4 on the other, or

A 3 on one die and a 3 on the other, or

A 4 on one die and a 2 on the other, or

A 4 on one die and a 5 on the other, or

A 5 on one die and a 1 on the other, or

A 5 on one die and a 4 on the other, or

A 6 on one die and a 3 on the other.

There are a total of 10 outcomes that satisfy this condition.

However, we have counted twice the outcomes that satisfy both conditions (i.e., the outcomes where the sum is both odd and a multiple of 3). There are 5 such outcomes: (1,2), (1,5), (5,1), (5,4), and (4,5).

Therefore, the total number of outcomes where the sum of the pair of dice is odd or a multiple of 3 is 18 + 10 - 5 = 23.

The probability of getting one of these outcomes is therefore 23/36.

Step-by-step explanation:

Answer:

4

Step-by-step explanation:

The equation for the volume of a sphere is [tex]\frac{4}{3}[/tex][tex]\pi r^3[/tex].

[tex]\frac{4}{3} \pi r^3 = 33.5[/tex]

[tex]r^3 = \frac{33.5*3}{4\pi} \\r = \sqrt[3]{\frac{33.5*3}{4\pi} }\\r = 2\\2 * r = 2 * 2 = 4[/tex]

Answer:

Step-by-step explanation:

Answer:

You can make 12 possible sundaes with these toppings.

Step-by-step explanation:

Chocolate, Vanilla, and Strawberry all have 4 possible outcomes:

1. Fudge & Chocolate Sprinkles

2. Fudge & Rainbow Sprinkles

3. Marshmallow & Chocolate Sprinkles

4. Marshmallow & Rainbow Sprinkles

-------------------------------------------------------------------------------------------------------------

4 x 3 will equal 12, the total possible sundaes you can make with these toppings and ice cream flavors.

Answer:

the 36th term is 187.

Step-by-step explanation:

To find the 36th term of a sequence, we need to know the rule that generates the sequence. Without that rule, we cannot find the 36th term.

However, if we assume that the sequence is an arithmetic sequence (meaning that there is a common difference between consecutive terms), we can use the given terms to find the common difference and then find the 36th term.

The common difference is found by subtracting the second term from the first term, or the third term from the second term.

Using the first and second terms, we get:

17 - 12 = 5

Using the second and third terms, we get:

22 - 17 = 5

Since both calculations give the same result, we can be confident that the common difference is 5.

Therefore, to find the 36th term, we can use the formula for the nth term of an arithmetic sequence:

an = a1 + (n - 1)d

where an is the nth term, a1 is the first term, n is the term number, and d is the common difference.

Using a1 = 12, d = 5, and n = 36, we get:

a36 = 12 + (36 - 1)5

a36 = 12 + 175

a36 = 187

So, if the sequence is an arithmetic sequence with a common difference of 5, then the 36th term is 187.

The balance in the account after 6 years is $2,466.69.

What is compound interest?

Compound interest is when you earn interest on both the money you've saved and the interest you earn.

We can use the formula for compound interest to find the balance in the savings account after 6 years:

[tex]A = P(1 + r/n)^{(nt)}[/tex]

where:

A is the balance in the account after t years

P is the initial deposit, which is $2,225

r is the annual interest rate, which is 1.625%

n is the number of times the interest is compounded per year, which is 4 (since it's compounded quarterly)

t is the number of years, which is 6

Plugging in these values, we get:

[tex]A = 2,225(1 + 0.01625/4)^{(4*6)}\\A = 2,225(1.0040625)^{24}[/tex]

A = 2,225(1.108227)

A = 2,466.69

Hence, the balance in the account after 6 years is $2,466.69.

To learn more about compound interest visit:

https://brainly.com/question/3989769

#SPJ1

The line graph of Greg's data wood look like "It would move upward."

A graph is a visual representation of data that shows the relationship between two or more variables. There are several types of graphs that can be used to display data

If Greg is measuring the height of the plant each day and the plant is continuing to grow for two weeks, then the line graph of his data would move upward. The graph would show an increasing trend as the plant grows taller each day. Therefore, the correct answer is "It would move upward."

To know  more about graph visit:

https://brainly.com/question/29629845

#SPJ1

The per square meter cost of steel will be $32. The solution has been obtained by using the cylinder.

What is a cylinder?

The cylinder, one of the most basic curvilinear geometric shapes, has long been considered to be a three-dimensional solid. It is regarded as a prism with a circle as its basis in elementary geometry.

We are given that the height of cylinder is 8 m and diameter is 10 m.

So, the radius is 5 m.

Now, using the surface area formula, we get

⇒ S = 2πrh + 2π[tex]r^{2}[/tex]

⇒ S = 2π * 5 * 8 + 2π * [tex]5^{2}[/tex]

⇒ S = 2 * 3.14 * 5 * 8 + 2 * 3.14 * 25

⇒ S = 251.2 + 157

⇒ S = 408.2 square meter

Now, it is given that the total cost of the steel will be $13,062.40.

So, per square meter cost will be:

⇒ Cost = [tex]\frac{13,062.40}{408.2\\}[/tex]

⇒ Cost = $32

Hence, the per square meter cost of steel for the cylinder will be $32.

Learn more about cylinder from the given link

https://brainly.com/question/27440983

#SPJ1

Answer:

40%

Step-by-step explanation:

2/5=x/100

cross multiply and you get 5x=200

by isolation the variable you will get x=40

therefore, 40% of Canadians read at least 10 books a year

We can write g in terms of f as: g(x) = f(x) - 3 = x² - 3

What is function?

In mathematics, a function is a relationship between two sets of elements, called the domain and the range, such that each element in the domain is associated with a unique element in the range. In simpler terms, a function is a set of rules that takes an input value and produces a corresponding output value.

To write g in terms of f, we can use function composition, which involves plugging the function f(x) into g(x) wherever we see x.

So, we have:

g(x) = f(x) - 3

where f(x) = x².

Substituting f(x) into g(x), we get:

g(x) = (x²) - 3

Therefore, we can write g in terms of f as:

g(x) = f(x) - 3 = x² - 3.

To learn more about functions from the given link:

https://brainly.com/question/12431044

#SPJ1

a. The number of red roses left t hours after the store opens [tex]R(t) = 400/2^{t/2}[/tex]    

b. The number of boxes of chocolate left t hours C(t) = 200 - 0.15t

c. One possible solution is t ≈ 7.546 hours after the store opens.

d. there are 194 boxes of chocolates left.

e. you need to arrive at the store no later than 7.504 hours after it opens.

a. The proportion (relative frequency) of times an event is anticipated to occur when an experiment is repeated a large number of times under identical conditions is known as the probability of the event.:

[tex]R(t) = 400/2^{t/2}[/tex]

b. Let C(t) be the quantity of boxes of chocolate left t hours after the store opens. At first, there are 200 boxes, of which 15% are purchased every hour. We can therefore write:

C(t) = 200 - 0.15t

c. We must solve the equation R(t) = C(t) in order to determine the time at which the number of boxes of chocolates and the number of roses are equal. We obtain: by substituting the formulas we discovered in parts a and b:

[tex]400/2^{t/2} = 200 - 0.15t[/tex]

Simplifying this equation, we get:

[tex]2^{t/2 + 1} + 0.15t - 400 = 0[/tex]

We can solve this equation numerically, using a calculator or a computer program. One possible solution is t ≈ 7.546 hours after the store opens.

d. At 12:30 in the early evening, which is 3.5 hours after the store opens, we can utilize the recipe we tracked down to some extent b to work out the quantity of boxes of chocolates left:

C(3.5) = 200 - 0.15(3.5) = 194.25

We ought to adjust this solution to appear to be legit with regards to the issue. Since we cannot have a fraction of a box, we can round to the nearest integer and state that there are 194 chocolate boxes remaining.

e. To buy 36 red roses, we need to solve the equation R(t) = 36. Substituting the formula we found in part a, we get:

[tex]400/2^{t/2}= 36[/tex]

Simplifying this equation, we get:

2^(t/2) ≈ 11.111

Taking the logarithm of both sides, we get:

t/2 ≈ log2(11.111)

t ≈ 2 log2(11.111)

Using a calculator, we get:

t ≈ 7.504 hours after the store opens.

Therefore, you must arrive at the store no later than 7.504 hours after it opens in order to purchase 36 red roses.

know more about logarithm visit:

https://brainly.com/question/30085872

#SPJ1

Answer: Let's say that the width of the rectangle is x meters. Then, according to the problem, the length of the rectangle is 6 meters longer than the width, which means that the length is (x + 6) meters.

The formula for the area of a rectangle is:

Area = Length x Width

We are given that the total area of the rectangle is 16m². Substituting the expressions for length and width, we get:

(x + 6) x = 16

Expanding the product and rearranging, we get a quadratic equation:

x² + 6x - 16 = 0

We can solve this equation by factoring or by using the quadratic formula. Factoring, we get:

(x + 8) (x - 2) = 0

This equation is satisfied when either x + 8 = 0 or x - 2 = 0. Therefore, the possible values for the width are x = -8 or x = 2. However, since the width of a rectangle cannot be negative, we reject the solution x = -8.

Therefore, the width of the rectangle is x = 2 meters. The length is 6 meters longer than the width, so the length is (2 + 6) = 8 meters.

Therefore, the dimensions of the rectangle are 2 meters by 8 meters.

Step-by-step explanation:

Ricky will have to wait for 26.78 years to have 200,000 in her account with this investment.

In order to determine the time it takes for Ricky's initial investment to grow to the desired amount, we can use the compound interest formula: A = P(1 + r/n)^(nt)

Where:

A is the final amount in the account (in this case, 200,000)

P is the initial investment (in this case, 20,000)

r is the annual interest rate (in this case, 0.09 for 9%)

n is the number of times interest is compounded per year (in this case, 1 for yearly compounding)

t is the number of years

We are trying to solve for t, so we can rearrange the formula to:

t = ln(A/P) / (n * ln(1 + r/n))

Plugging in the values:

t = ln(200,000/20,000) / (1 * ln(1 + 0.09/1))

t = ln(10) / ln(1.09)

t ≈ 2.303 / 0.086

t ≈ 26.78

Ricky will have to wait approximately 26.78 years to have 200,000 in her account with this investment.

Find more exercises on calculating compounded interest of investments;

https://brainly.com/question/21598629

#SPJ1

In the exponential function F(x) = ab^x, the variable x is an exponent.

In the exponential function F(x) = ab^x, the variable x is an exponent.

The function F(x) represents a value that grows or decays exponentially with respect to x.

The base b is a positive constant that determines the rate of growth or decay, and the coefficient a determines the initial value of the function.

The variable x can be any number

However, it is always the exponent that determines the value of the function F(x) for a given input x.

Therefore, the correct answer is A. an exponent.

Read more about exponential functions at

https://brainly.com/question/2456547

#SPJ1

The surface area of cylinder M is approximately 131.95 square feet and the surface area of cylinder N is approximately 319.77 square feet.

What is a cylinder?

A cylinder is a three-dimensional geometric shape that consists of two congruent parallel bases in the shape of circles or ellipses, and a curved surface that connects the bases. The height of a cylinder is the perpendicular distance between the bases. A cylinder is a type of prism, and it can be classified as either a right cylinder or an oblique cylinder depending on whether or not its axis is perpendicular to its bases. Right cylinders have circular bases and their axis is perpendicular to the bases, while oblique cylinders have elliptical bases and their axis is not perpendicular to the bases.

Now,

Let the radius of cylinder M be r and its height be h. Then, the radius and height of cylinder N are both 2r, since the radius is equal to the height.

Since the cylinders are similar, their dimensions are proportional, which means:

(height of N) / (height of M) = 5/3

(radius of N) / (radius of M) = (2r) / r = 2

Using the formula for the surface area of a cylinder, we can write:

Surface area of cylinder M: 2πr² + 2πrh

Surface area of cylinder N: 2π(2r)² + 2π(2r)(5/3)h

We are told that the surface area of cylinder N is 256 square feet greater than the surface area of cylinder M. So we can set up the equation:

2π(2r)² + 2π(2r)(5/3)h = 2πr² + 2πrh + 256

Simplifying and solving for h, we get:

4r² + 20rh/3 = r² + rh + 128

3r² - rh - 128 = 0

(3r + 32)(r - 4) = 0

Since the height of the cylinder cannot be negative, we take the positive solution r = 4. Then, the height of cylinder M is (3/5)(4) = 12/5, and the height of cylinder N is 2(4) = 8.

Using the formulas for surface area, we can find the surface areas of both cylinders:

Surface area of cylinder M: 2π(4)² + 2π(4)(12/5) = 131.95 square feet

Surface area of cylinder N: 2π(2(4))² + 2π(2(4))(8) = 319.77 square feet

Therefore, the surface area of cylinder M is approximately 131.95 square feet and the surface area of cylinder N is approximately 319.77 square feet.

To know more about cylinder visit the link

brainly.com/question/16134180

#SPJ1