Graph the function: f(x) = -2 for x< 1. Show a T-chart with all of your work. Determine a solution that is part of the
function for the given interval.
Answers
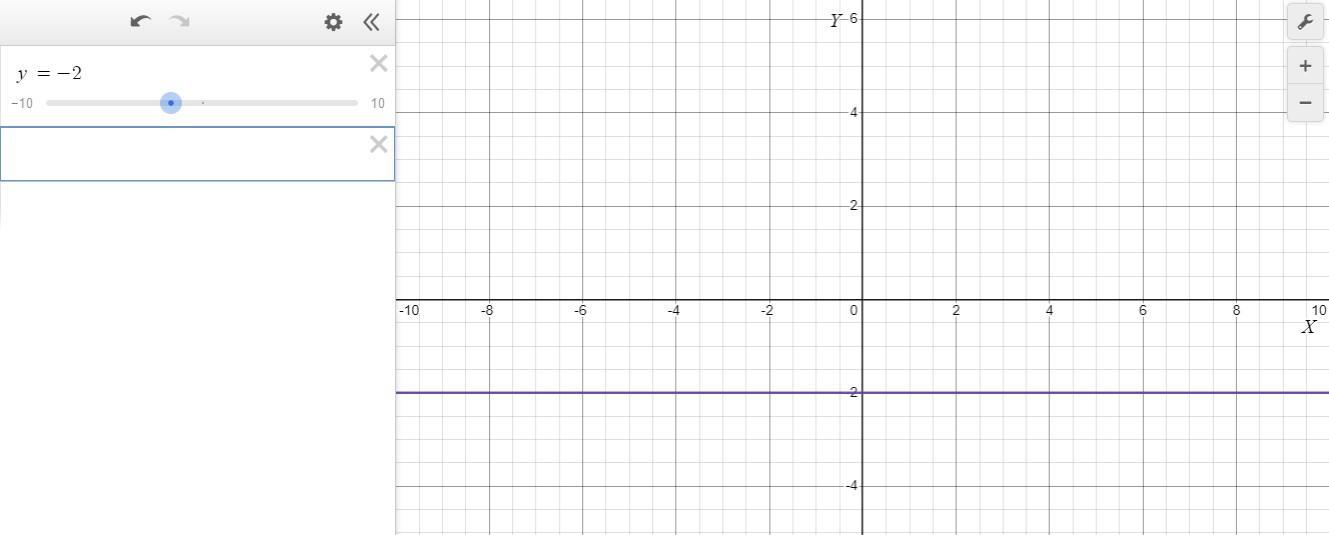
The graph of the given function f(x) = -2 is as attached .
How to graph a function?The general formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
We are given the function as:
f(x) = -2
Thus, this means that the graph will be a straight horizontal line cutting across the point -2 on the y-axis which is indicated in the graph attached
Read more about Function Graph at: https://brainly.com/question/4025726
#SPJ1
Related Questions
Find a degrees. a 12 13 5
Answers
In the given triangle, α is equal to 67.36°.
What is a triangle's definition?
A triangle is a two-dimensional closed geometric form that has three sides, three angles, and three vertices (corners). It is the most basic polygon, produced by joining any three non-collinear points in a plane. The sum all angles of a triangle is always 180°. Triangles are classed according to their side length (equilateral, isosceles, or scalene) and angle measurement (acute, right, or obtuse).
Now,
Using Trigonometric functions
We can use the sine function
So,
Sin α=Perpendicular/Hypotenuse
Sin α = 12/13
α=67.36°
Hence,
The value of α will be 67.36°.
To know more about triangles visit the link
brainly.com/question/2773823
#SPJ1
Simplify (3x3y2 − 5xy4 − 2xy) + (2x3y2 + 5xy4 + 3xy).
5x3y2 − 2xy4 + xy
5x3y2 − 2xy4 − 5xy
5x3y2 + xy
5x3y2 − xy
Answers
The terms that have the same variables raised to the same powers are:
3x^3y^2 and 2x^3y^2, which add up to 5x^3y^2
-5xy^4 and 5xy^4, which cancel each other out
-2xy and 3xy, which add up to xy
Putting these like terms together, we get:
(3x^3y^2 - 5xy^4 - 2xy) + (2x^3y^2 + 5xy^4 + 3xy) = 5x^3y^2 + xy
Therefore, the simplified expression is 5x^3y^2 + xy.
Answer:
the first one: 5x3y2 - 2xy4 +xy
Step-by-step explanation:
hope it helps :)
What is the total surface area of the figure shown?
Answers
The total surface area of the given figure is 619.2 in², which is not listed in the provided options.
Give a brief account on total surface area.The surface area is known to be measure of the total area occupied by the surface of the object. Defining the surface area mathematically in the presence of a curved surface is better than defining the arc length of a one-dimensional curve, or the surface area of a polyhedron (i.e. an object with flat polygonal faces). Much more complicated. For a smooth surface sphere such as the following, surface area is assigned using representation as a parametric surface. This surface definition is based on calculus and includes partial derivatives and double integrals.
The triangular face of the given figure represent an equilateral triangle of sides 12 in.
Area of the triangle = (√3/4) × a²
Area of the triangular face:
= (√3/4) × 12²
= (√3/4) × 144
= 57.6 in²
Area of the rectangle = Length × width
Area of the rectangular face:
= 12 × 14
= 168 in²
Area of the given figure:
= (2 × 57.6) + (3 × 168)
= 115.2 + 504
= 619.2 in²
To know more about polygonal faces, visit:
https://brainly.com/question/16550007
#SPJ1
A recent conference had 900 people in attendance. In one exhibit room of 80 people, there were 65 teachers and 15 principals. What prediction can you make about the number of principals in attendance at the conference?
There were about 820 principals in attendance.
There were about 731 principals in attendance.
There were about 208 principals in attendance.
There were about 169 principals in attendance.
Answers
The answer is: There were about 169 principals in attendance.
what is proportion?
In mathematics, a proportion is an equation that states that two ratios or fractions are equal. A proportion can be written in the form of a/b = c/d, where a, b, c, and d are numbers or variables.
Proportions are used to compare two or more quantities or to find an unknown value. For example, if we know that the ratio of the length of a rectangle to its width is 2:1, and we also know that the length is 6 feet, we can use a proportion to find the width. We set up the proportion as 2/1 = 6/w, where w is the width of the rectangle, and then solve for w by cross-multiplying and simplifying the equation.
Proportions are also used in many real-world applications, such as cooking, finance, and science.
To make a prediction about the number of principals in attendance at the conference, we need to use the given information and make some assumptions.
We know that in one exhibit room of 80 people, there were 15 principals. Let's assume that this exhibit room is representative of the entire conference, and that the proportion of principals to attendees in this room is the same as the proportion of principals to attendees in the entire conference.
Using this assumption, we can set up a proportion:
15 principals / 80 attendees = x principals / 900 attendees
To solve for x, we can cross-multiply and simplify:
15 * 900 = 80 * x
x = (15 * 900) / 80 = 168.75
So our prediction is that there were about 169 principals in attendance at the conference.
Therefore, the answer is: There were about 169 principals in attendance.
To learn more about ratios and proportions from the given link
https://brainly.com/question/29774220
#SPJ1
Find the surface area of the sphere. Use 3.14 for pi.
sphere is 7 yd
Answers
an object is 19.0 cm from the center of a spherical silvered-glass christmas tree ornament 6.00 cm in diameter. What is the position of its image (counting from the ornament surface)?
Answers
The position of the image is approximately 1.71 cm from the ornament's surface.
To determine the position of the image, we need to use the mirror formula for a concave mirror, which is \frac{1}{f} = [tex]\frac{1}{do} + \frac{1}{di},[/tex] where f is the focal length, do is the object distance, and di is the image distance.
First, we need to find the focal length (f) of the spherical ornament. The radius of curvature (R) is half the diameter, so R = 6.00 cm / 2 = 3.00 cm. For a spherical mirror, the focal length is half the radius of curvature: f = R/2 = 3.00 cm / 2 = 1.50 cm.
Next, we need to find the object distance (do). The object is 19.0 cm from the center of the ornament, but we need the distance from the ornament's surface. Since the radius is 3.00 cm, we subtract that from the total distance: do = 19.0 cm - 3.00 cm = 16.0 cm.
Now, we can use the mirror formula:
\frac{1}{f} = [tex]\frac{1}{do} + \frac{1}{di},[/tex]
1/1.50 cm = 1/16.0 cm + 1/di
To solve for di, subtract 1/16.0 cm from both sides and then take the reciprocal:
1/di = 1/1.50 cm - 1/16.0 cm
di ≈ 1.71 cm
The position of the image is approximately 1.71 cm from the ornament's surface.
learn more about the mirror formula for a concave mirror,
https://brainly.com/question/3555871
#SPJ11
The position of the image is 20.8 cm from the center of the spherical ornament, counting from the ornament surface.
To find the position of the image, we can use the mirror equation:
1/o + 1/i = 1/f
where o is the object distance from the center of the spherical ornament, i is the image distance from the center of the spherical ornament, and f is the focal length of the ornament.
Since the ornament is a spherical mirror, the focal length is half the
radius of curvature, which is half the diameter of the ornament:
f = R/2 = 6.00 cm/2 = 3.00 cm
Substituting the given values, we get:
1/19.0 cm + 1/i = 1/3.00 cm
Solving for i, we get:
1/i = 1/3.00 cm - 1/19.0 cm = (19.0 cm - 3.00 cm)/(3.00 cm x 19.0 cm) = 0.0481 cm^-1
i = 1/0.0481 cm = 20.8 cm
Therefore, the position of the image is 20.8 cm from the center of the
spherical ornament, counting from the ornament surface.
for such more question on ornament surface
https://brainly.com/question/30938695
#SPJ11
Need help!! Xxxxxxxx
Answers
The amount of people infected after t weeks is modeled by the function presented as follows:
[tex]f(t) = \frac{675000}{1 + 4000e^{-t}}[/tex]
When the epidemic began, we have that t = 0, hence the number of people is given as follows:
f(0) = 675,000/(1 + 4000)
f(0) = 169 people.
Six weeks after the epidemic began, we have that t = 6, hence the number of people is given as follows:
f(6) = 675,000/(1 + 4000 x e^(-6))
f(6) = 61,841 people.
The limiting size of the infected population is the numerator of the fraction, which is 675,000, as the denominator goes to zero when t goes to infinity.
More can be learned about exponential functions at https://brainly.com/question/2456547
#SPJ1
In ΔUVW, w = 1. 4 cm, m m∠W=63° and m m∠U=29°. Find the length of v, to the nearet 10th of a centimeter
Answers
The length of v, to the nearest 10th of a centimeter is 2.2.
To find the length of side v in triangle UVW, we can use the law of sines, which states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in the triangle.
Using this formula, we have,
v/sin(m∠V) = w/sin(m∠W)
We know that w = 1.4 cm and m∠W = 63°. To find sin(m∠W), we can use a calculator,
sin(63°) ≈ 0.89
Substituting the values we know into the formula, we get,
v/sin(m∠V) = 1.4/0.89
To solve for v, we need to find sin(m∠V). We know that the sum of the angles in a triangle is 180°, so we can find m∠V by subtracting the measures of the other two angles from 180°,
m∠V = 180° - m∠U - m∠W
m∠V = 180° - 29° - 63°
m∠V = 88°
Now, we can substitute the value of sin(m∠V) into the equation and solve for v,
v/ sin(88°) = 1.4/0.89
v ≈ 2.2 cm
Therefore, the length of side v in triangle UVW is approximately 2.2 cm to the nearest tenth of a centimeter.
To learn more about length here:
https://brainly.com/question/16537545
#SPJ4
Answer:
1.6
Step-by-step explanation: This is answer on DeltaMath
let f(x)=∫x2−3x−2et2dt. at what value of x is f(x) a minimum?
a. ½
b. 3/2
c. 2
d. 3
Answers
The value of x at which f(x) is a minimum is 3/2.
To find the minimum value of f(x), we need to calculate its derivative and set it equal to zero.
So,
[tex]f(x) = ∫(x^2 - 3x - 2) e^(t^2) dt[/tex]
Taking the derivative of f(x) with respect to x, we get:
[tex]f'(x) = 2x e^(x^2 - 3x - 2) - 3 e^(x^2 - 3x - 2)[/tex]
Setting f'(x) equal to zero:
[tex]2x e^(x^2 - 3x - 2) - 3 e^(x^2 - 3x - 2) = 0[/tex]
Factorizing, we get:
[tex]e^(x^2 - 3x - 2) (2x - 3) = 0[/tex]
So, either e[tex]^(x^2 - 3x - 2)[/tex]= 0 (which is not possible), or
2x - 3 = 0
Solving for x, we get:
x = 3/2
Therefore, the value of x at which f(x) is a minimum is 3/2.
Learn more about derivative
https://brainly.com/question/30365299
#SPJ4
f'(x) changes from negative to positive at x = 2.105, we know that f(x) has a local minimum at x = 2.105.
Therefore, the answer is c. 2.
To find the value of x at which f(x) is a minimum, we need to find the critical points of f(x) and then determine whether each critical point is a minimum or maximum using the first derivative test.
To find the critical points of f(x), we need to find where f'(x) = 0. Using the Fundamental Theorem of Calculus and the Chain Rule, we can find that:
[tex]f'(x) = 2x - 3 - 2xe^{(x^2-3x-2t^2)}[/tex]
To find where f'(x) = 0, we need to solve the equation[tex]2x - 3 - 2xe^{x^2-3x-2t^2} = 0[/tex] for x. Unfortunately, this equation cannot be solved algebraically, so we need to use numerical methods. One way to do this is to use a graphing calculator or computer program to graph y = 2x - 3 and[tex]y = 2xe^{x^2-3x-2t^2)[/tex]and find their intersection(s).
Using this method, we can find that there is only one critical point, which is approximately x = 2.105. To determine whether this critical point is a minimum or maximum, we need to use the first derivative test. Since f'(x) changes from negative to positive at x = 2.105, we know that f(x) has a local minimum at x = 2.105.
Therefore, the answer is c. 2.
learn more about local minimum
https://brainly.com/question/10878127
#SPJ11
Mack's Toy Shop made 600 trains yesterday and found that 30 were defective. They
plan to make 4,500 trains this week.
Using the information given, how many trains are expected to be defective?
225 trains
6,000 trains
15 trains
500 trains
Answers
Answer:
225 trains
Step-by-step explanation:
since they are using the same process and materials, we expect them to have the same ratio between trains made and defective trains :
600 / 30 = 20/1
one out of 20 is defect.
so, when they make 4500 trains, we need to divide this by 20 to get the number of expected defective trains :
4500 / 20 = 225
I find the answer option of 6000 defective trains really funny : if that were true, more than the produced trains (4500) would be defective. how ... ?
The mass of Earth is approximately 5.97 x 1024 kilograms. The mass of Venus is approximately 4,870,000,000,000
kilograms. What is the difference between the approximate masses, in kilograms, of Earth and Venus? Express your
answer in scientific notation.
Answers
Therefore, the difference in mass between Earth and Venus is approximately 5.96513 x 10^24 kilograms.
Mass of venus calculation.
The difference in mass between Earth and Venus is:
5.97 x 10^24 kg - 4.87 x 10^12 kg
To subtract these two values, we need to express them in the same scientific notation. Since 4.87 x 10^12 is much smaller than 5.97 x 10^24, we can express it in scientific notation with the same exponent as the mass of Earth:
4.87 x 10^12 kg = 0.00487 x 10^24 kg
Now we can subtract the two values:
5.97 x 10^24 kg - 0.00487 x 10^24 kg = 5.96513 x 10^24 kg
Therefore, the difference in mass between Earth and Venus is approximately 5.96513 x 10^24 kilograms.
Learn more about mass of Venus below.
https://brainly.com/question/9010477
#SPJ1
6. Kaylee borrows $700 from her dad to buy a new phone.
She has to pay him back in 24 months with a 2% simple
interest rate. How much inter
interest rate. How much interest will she have to pay?
Answers
Kaylee will have to pay $28 in interest.
What is simple interest?The interest on a loan or principal sum can be easily calculated using simple interest. Simple interest is a notion that is employed across a wide range of industries, including banking, finance, automobiles, and more.
The interest Kaylee will have to pay is calculated as follows:
Interest = Principal x Rate x Time
where Principal is the amount borrowed, Rate is the interest rate as a decimal, and Time is the time period in years. Since Kaylee has to pay back the loan in 24 months, or 2 years, we can plug in the given values to get:
Interest = 700 x 0.02 x 2 = $28
Therefore, Kaylee will have to pay $28 in interest.
Learn more about simple interest on:
https://brainly.com/question/1173061
#SPJ9
if the florida distirution is also approximately morlam, but with a standard deviation of 2.9 inches, what is the mean height of a football player on this florida team? ap stat
Answers
To find the mean height of a football player on this Florida team, we need to know the mean of the normal distribution (Morlam) and the standard deviation of the Florida distribution. Since the Florida distribution is also approximately normal (Morlam) with a standard deviation of 2.9 inches, we can use the Empirical Rule to estimate the mean height.
According to the Empirical Rule, approximately 68% of the data falls within one standard deviation of the mean, approximately 95% within two standard deviations, and approximately 99.7% within three standard deviations. Since we know that the standard deviation of the Florida distribution is 2.9 inches, we can assume that the mean height falls within three standard deviations of the mean.
So, if we assume that the mean height is at the centre of the distribution, we can estimate it by adding and subtracting three standard deviations from it. Therefore, the mean height of a football player on this Florida team can be estimated to be:
Mean height = Mean of the Morlam distribution ± 3 x Standard deviation of the Florida distribution
Mean height = Mean of the Morlam distribution ± 3 x 2.9 inches
Without knowing the mean of the Morlam distribution, we cannot calculate the exact mean height. However, if we assume that the Morlam distribution has a mean height of 70 inches (a typical average height for a football player), then the mean height of a football player on this Florida team can be estimated to be:
Mean height = 70 ± 3 x 2.9
Mean height = 70 ± 8.7
Mean height = 61.3 to 78.7 inches
Therefore, we can estimate that the mean height of a football player on this Florida team is between 61.3 and 78.7 inches.
Learn more about Normal Distribution here: brainly.com/question/17199694
#SPJ11
We can estimate that the mean height of a football player on the Florida team is approximately 70 inches.
To find the mean height of a football player on the Florida team, we need to know the exact distribution of heights. However, since we only have information about the standard deviation and the fact that it is approximately normal, we can make an educated guess that the distribution is still normal with a mean somewhere close to the national average of 70 inches.
Using the empirical rule, we know that about 68% of the data falls within one standard deviation of the mean. In this case, one standard deviation is 2.9 inches.
So, we can assume that about 68% of the heights on the Florida team fall between (70-2.9) = 67.1 inches and (70+2.9) = 72.9 inches.
If we assume that the distribution is symmetric, we can estimate the mean height of the Florida team by taking the average of the lower and upper bounds of the interval: (67.1 + 72.9)/2 = 70 inches.
For similar question on mean.
https://brainly.com/question/23251787
#SPJ11
The list represents a student's grades on tests in their math class.
47, 85, 82, 63, 77, 79, 58, 95, 72, 90
Find the range for the data set.
Answers
In this case, the smallest grade is 47, and the largest grade is 95. So the range is:
95 - 47 = 48
Therefore, the range for the given data set is 48.
The range for the data set is equal to 48.
What is a range?In Mathematics and Statistics, a range is the difference between the highest number and the lowest number contained in a data set.
In Mathematics and Statistics, the range of a data set can be calculated by using this mathematical expression;
Range = Highest number - Lowest number
From the given data set, we have:
Highest number = 95.
Lowest number = 47.
By substituting, we have:
Range = 95 - 47
Range = 48.
Read more on range here: brainly.com/question/32352196
#SPJ2
The trinomial x^2 - 11x + 18 is equivalent to
Answers
the equivalent form of the trinomial x² - 11x + 18 is (x - 2)(x - 9). We can verify this by multiplying the two binomials using the distributive property:
How to solve the question?
The given trinomial is x² - 11x + 18. To find an equivalent form, we can factorize the trinomial by finding two binomials whose product is equal to the trinomial.
We can start by finding two factors of 18 that add up to -11, the coefficient of x. The factors of 18 are 1, 2, 3, 6, 9, and 18. We can see that 9 and 2 are the two factors that add up to -11. So, we can write:
x² - 11x + 18 = (x - 2)(x - 9)
Therefore, the equivalent form of the trinomial x² - 11x + 18 is (x - 2)(x - 9). We can verify this by multiplying the two binomials using the distributive property:
(x - 2)(x - 9) = x(x - 9) - 2(x - 9) = x² - 9x - 2x + 18 = x² - 11x + 18
So, we have successfully found the equivalent form of the given trinomial.
To know more about trinomial visit :-
https://brainly.com/question/27020215
#SPJ1
The function g(x) is shown on the graph.
The graph shows an upward opening parabola with a vertex at negative 4 comma 3, a point at negative 6 comma 7, and a point at negative 2 comma 7.
What is the equation of g(x) in vertex form?
g(x) = (x − 4)2 − 3
g(x) = (x − 4)2 + 3
g(x) = (x + 4)2 − 3
g(x) = (x + 4)2 + 3
Answers
The equation of g(x) in parabola vertex form is g(x) = (x + 4)^2 + 3. Option (D) is the correct answer.
Parabola calculation.
Since the vertex of the parabola is at (-4, 3), we can write the equation of the parabola in vertex form as:
g(x) = a(x + 4)^2 + 3
where "a" is a constant that determines the shape of the parabola. Since the parabola opens upward, "a" must be positive.
We also know that the parabola passes through the points (-6, 7) and (-2, 7). Substituting these values into the equation above, we get:
7 = a(-6 + 4)^2 + 3
7 = 4a + 3
4a = 4
a = 1
Substituting "a = 1" into the equation above, we get:
g(x) = (x + 4)^2 + 3
Therefore, the equation of g(x) in vertex form is g(x) = (x + 4)^2 + 3. Option (D) is the correct answer.
Learn more about parabola below.
https://brainly.com/question/25651698
#SPJ1
please someone help and give answers !!!
Answers
16.) Mean average deviation= option C
17.) Range of a data set = option E.
18.) First quartile = opinion AB
19.) Second quartile = option B
20.) Third quartile = option A
21.) Interquartile range = option D
How to determine the measures of the spread?
To determine the measures of the spread is to match their various definitions to the correct measures given such as follows:
16.) Mean average deviation: The average deviation of data from the mean.
17.) Range of a data set : The difference between the highest value and the lowest value in a numerical data set.
18.) First quartile: The median in the lower half.
19.) Second quartile: The median value in a data set.
20.) Third quartile: The median in the upper half.
21.) Interquartile range: The distance between the first and the third quartile.
Learn more about range here:
https://brainly.com/question/26098895
#SPJ1
4y = -x - 32 (Show work)
Answers
Answer: the solution for y in terms of x is y = (-1/4)x - 8.
Step-by-step explanation: In order to obtain a solution for y in the given equation of 4y = -x - 32, it is imperative to achieve the isolation of y on a singular side of the equation. To accomplish this task, it is possible to perform division on both sides of the equation by a factor of 4:
The given equation 4y/4 = (-x - 32)/4 can be expressed in an academic manner as follows: The given equation reveals that the quotient of 4y divided by 4 is equivalent to the quotient of the opposite of x added to negative 32, also divided by 4.
Upon performing simplification, the expression on the right-hand side yields:
The equation y = (-1/4)x - 8 can be expressed in an academic manner as follows: The dependent variable y is equivalent to the product of the constant (-1/4) and the independent variable x, with an additional decrement of eight.
An electronic book device had a value of t dollars before a holiday. The value decreased by 15% after the holiday. Which expressions show the value of the electronic book device after the holiday? Select all the expressions that apply.
A. 1.15
B. 0.85
C. −0.15
D. 1−0.15
E. −0.85
F. (1−0.15)
Answers
The expressions that correctly show the value of the electronic book device after the holiday are B and D, which represent the percentage decrease of 15% as 0.85 (or 1-0.15).
Which expressions show the value of the electronic book device after the holiday?The value of an electronic book device before a holiday is represented by the variable t. After the holiday, the value of the device decreased by 15%. To find the value of the device after the holiday, we need to multiply the original value by the percentage decrease, which is 0.85 (or 1-0.15). Therefore, the expressions that correctly show the value of the electronic book device after the holiday are B and D.
Option A (1.15) represents the percentage increase and not the decrease, so it is incorrect. Option C (-0.15) represents the percentage decrease, but it cannot be used alone to find the new value. Option E (-0.85) is the negative of the percentage decrease, so it is also incorrect. Finally, option F is equivalent to option D, so it is also correct.
In summary, the expressions that correctly show the value of the electronic book device after the holiday are B and D, which represent the percentage decrease of 15% as 0.85 (or 1-0.15).
to know more about electronic
brainly.com/question/1255220
#SPJ1
Use substitution to sole the system of equations
Answers
Answer:
(0, 0)
(4, 16)
Step-by-step explanation:
[tex]y = 4x[/tex]
[tex]y = x^2[/tex]
Using substitution, we can replace y in the second equation with 4x from the first equation.
[tex]4x = x^2[/tex]
Now, we can move all the x's to one side and complete the square to solve for x.
[tex]0 = x^2 - 4x[/tex]
↓ adding 4 to both sides
[tex]4 = x^2 - 4x + 4[/tex]
↓ factoring the right side
[tex]4 = (x-2)^2[/tex]
↓ taking the square root of both sides
[tex]\sqrt4 = \sqrt{(x-2)^2[/tex]
[tex]\pm2 = x - 2[/tex]
↓ adding 2 to both sides
[tex]2 \pm 2 = x[/tex]
[tex]\boxed{x = 0 \ \ \ \text{or} \ \ \ x = 4}[/tex]
Then, we can solve for y by plugging both x-values into the first equation.
[tex]y = 4(0)[/tex] or [tex]y = 4(4)[/tex]
[tex]\boxed{y = 0 \ \ \ \text{or} \ \ \ y=16}[/tex]
Finally, we can form two ordered pairs that are the solutions to the system of equations.
[tex]\boxed{(0,0)}[/tex]
[tex]\boxed{(4,16)}[/tex]
What is the range of f? A coordinate plane. The x- and y-axes both scale by one. The graph of the function f starts at negative six, negative two, which is plotted. Then is decreases at a non linear rate to negative five, negative five, where it increases at a non linear rate to negative two, one and one-half. At two, one and one-half the function decreases at a non linear rate through the origin and to the point two, negative one and one-half. Then the function increases at a non linear rate until five, five, which is plotted.
A coordinate plane. The x- and y-axes both scale by one. The graph of the function f starts at negative six, negative two, which is plotted. Then is decreases at a non linear rate to negative five, negative five, where it increases at a non linear rate to negative two, one and one-half. At two, one and one-half the function decreases at a non linear rate through the origin and to the point two, negative one and one-half. Then the function increases at a non linear rate until five, five, which is plotted.
Choose 1 answer:
(Choice A) The f(x)-values -6, -3, 0, 2, and 5
(Choice B) The f(x)-values -5, -2, 0, 2, and 5
(Choice C) -6 ≤ f(x) ≤ 5
(Choice D) − 5 ≤ f(x) ≤ 5
Answers
The range of f include the following: D. -5 ≤ f(x) ≤ 5.
What is a domain?In Mathematics and Geometry, a domain is the set of all real numbers for which a particular function is defined.
Additionally, the vertical extent of any graph of a function represents all range values and they are always read and written from smaller to larger numerical values, and from the bottom of the graph to the top.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = {-6, 5} or -6 ≤ x ≤ 5.
Range = {-5, 5} or -5 ≤ f(x) ≤ 5.
Read more on domain here: brainly.com/question/17440903
#SPJ1
in the regression of the general fertility rate (gfr) on the tax personal exemption (pe) and its first lag the fitted regression is: what is the impact propensity?
Answers
The impact propensity can be interpreted as the slope coefficient for the tax personal exemption (pe) or its first lag in
the regression equation.
To determine the impact propensity in the regression of the general fertility rate (GFR) on the tax personal exemption
(PE) and its first lag, you should follow these steps:
Estimate the regression model using the available data. The model should look like this:
GFR = β0 + β1 × PE + β2 × PE_lag + ε
Where GFR is the general fertility rate, PE is the tax personal exemption, PE_lag is the tax personal exemption's first
lag, and ε is the error term.
Obtain the estimated coefficients (β0, β1, and β2) from the fitted regression model.
These coefficients will help you determine the impact propensity.
Calculate the impact propensity. The impact propensity in this context refers to the change in the general fertility rate
resulting from a one-unit increase in the tax personal exemption, taking into account both its current and lagged
effects.
To find the impact propensity, sum the coefficients for the tax personal exemption and its first lag:
Impact propensity = β1 + β2
for such more question on propensity
https://brainly.com/question/20376297
#SPJ11
Simplify the expression (−1 3/4)^2 - √ [127−2(3)]
Answers
On simplifying the expression (−1 3/4)²- √ [127−2(3)] we get -127/16
Simplifying an expression:
To simplify the expression, we need to follow the order of operations, which is PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
First, we simplify the exponent by squaring -1 3/4 to get 49/16. Then, we simplify the expression under the square root by subtracting 2 times 3 from 127 to get 121, and we take the square root of 121 to get 11.
Here we have
(−1 3/4)²- √ [127−2(3)]
The above expression can be simplified as follows
=> (−1 3/4)²- √ [127−2(3)]
Convert the mixed fraction into an improper fraction
=> 1 3/4 = 7/4 [ ∵ 4 × 1 + 3 = 7 ]
So given expression can be
=> (−7/4)²- √ [127−2(3)]
=> (49/16) - √ [121]
=> (49/16) - 11
=> (49 - 176 /16)
=> -127/16
Therefore,
On simplifying the expression (−1 3/4)²- √ [127−2(3)] we get -127/16
Learn more about Expression at
https://brainly.com/question/30148250
#SPJ1
of the cartons produced by a company, 3% have a puncture, 6% have a smashed corner, and 1.4% have both a puncture and a smashed corner. find the probability that a randomly selected carton has a puncture or a smashed corner.
Answers
The probability that a randomly selected carton has a puncture or a smashed corner is 0.076, or 7.6%.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
To find the probability that a randomly selected carton has a puncture or a smashed corner, we can use the formula:
P(puncture or smashed corner) = P(puncture) + P(smashed corner) - P(puncture and smashed corner)
where P(puncture) is the probability of a carton having a puncture, P(smashed corner) is the probability of a carton having a smashed corner, and P(puncture and smashed corner) is the probability of a carton having both a puncture and a smashed corner.
Substituting the given probabilities into the formula, we get:
P(puncture or smashed corner) = 0.03 + 0.06 - 0.014
P(puncture or smashed corner) = 0.076
Therefore, the probability that a randomly selected carton has a puncture or a smashed corner is 0.076, or 7.6%.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
A brick has a mass of 2,022.75 grams and a volume of 1,064.5 cubic centimeters.
What is the density of the brick, in grams per cubic centimeter (³) ²¹
g
cm
3
Round your answer to the nearest tenth.
Answers
Answer:
To find the density of the brick, we need to divide its mass by its volume:
density = mass / volume
Plugging in the values given in the problem, we get:
density = 2,022.75 g / 1,064.5 cm³
Simplifying the division, we get:
density = 1.8996 g/cm³
Rounding to the nearest tenth, we get:
density ≈ 1.9 g/cm³
Therefore, the density of the brick is approximately 1.9 grams per cubic centimeter (g/cm³).
Identify an equation in standard form for an ellipse with its center at the origin, a vertex at (0, 6), and a co-vertex at (2, 0).
Answers
the equation of the ellipse with center at the origin, a vertex at (0, 6), and a co-vertex at (2, 0) is:(x² / 36) + (y² / 4) = 1
How to solve the question?
To write the equation of an ellipse in standard form when the center is at the origin, we need to use the following formula:
(x²/ a²) + (y² / b²) = 1
where a is the distance from the center to a vertex, and b is the distance from the center to a co-vertex.
In our problem, the center is at the origin, and a vertex is located at (0, 6), so the distance from the center to a vertex is 6. Therefore, we have:
a = 6
Similarly, a co-vertex is located at (2, 0), so the distance from the center to a co-vertex is 2. Therefore, we have:
b = 2
Substituting these values into the formula above, we get:
(x² / 6²) + (y² / 2²) = 1
Simplifying, we get:
(x² / 36) + (y² / 4) = 1
Therefore, the equation of the ellipse with center at the origin, a vertex at (0, 6), and a co-vertex at (2, 0) is:
(x² / 36) + (y² / 4) = 1
This is the equation in standard form for an ellipse with a horizontal major axis (since a is greater than b), and it represents an ellipse that is taller than it is wide. The major axis of the ellipse is the line passing through the vertices, which in this case is the y-axis, and the minor axis is the line passing through the co-vertices, which in this case is the x-axis.
To know more about vertex visit :-
https://brainly.com/question/29476657
#SPJ1
jacobi measured the diagonals of three tv screens as 5 square roots of 84 inches, 46 2/3 inches, and 46.625 inches. which shows the length of the diagonals in ascending order
Answers
The length of the diagonals in ascending order is: 140/3 inches
What is algebra?Algebra is a branch of mathematics that deals with mathematical operations and symbols to represent numbers and their relationships. It involves the use of variables, which are letters or symbols that represent unknown or unspecified quantities, and manipulating equations and expressions to solve problems.
To compare the lengths of the diagonals of the three TV screens, we can simplify each expression and put them in order:
5 square roots of 84 inches
= 5 * √(4 * 21) inches
= 10 * √(21) inches
46 2/3 inches
= 140/3 inches
46.625 inches
Therefore, the length of the diagonals in ascending order is:
46.625 inches < 140/3 inches < 10 * √(21) inches
Note that we can also write the second diagonal as a mixed number, which is the form of a whole number and a fraction:
140/3 inches
= 46 2/3 inches
To learn more about algebra from the given link
https://brainly.com/question/24875240
#SPJ1
what are the odds of throwing three dice together, that exactly two of the three resulting numbers will match?
Answers
As three dice are thrown together and the probability of any two of them being the same will be 5/12.
When a dice is thrown there are 6 possible outcomes. So, when three dice are thrown, the number of outcomes will be 6× 6× 6 = 216.
The probability of a number repeating = ₆C₂ = (6×5)/2 = 15
So each number will have possible 15 outcomes.
6 numbers will have 6 × 15 outcomes = 90 outcomes
So probability = Number of desired outcomes/ total number of outcomes = 90 / 216 = 5/12
So the probability of any two number matches when three dices are thrown together will be 5/12.
For more information regarding probability, kindly refer
https://brainly.com/question/31120123
#SPJ4
how can the power series method be used to solve the nonhomogeneous equation, about the ordinary point ? carry out your idea by solving the equation. you can either attach your work or type in your work.
Answers
The power series method can be used to solve a nonhomogeneous differential equation about an ordinary point by finding both a homogeneous and particular solution using a series expansion and the method of undetermined coefficients.
The power series method is a technique used to find a series solution of a differential equation. When applied to a nonhomogeneous differential equation, the method involves finding both a homogeneous solution and a particular solution.
Assuming that the nonhomogeneous differential equation has the form
y''(x) + p(x)y'(x) + q(x)y(x) = f(x)
where p(x), q(x), and f(x) are functions of x, we can begin by finding the solution to the associated homogeneous equation
y''(x) + p(x)y'(x) + q(x)y(x) = 0
Using the power series method, we can assume a solution of the form:
y(x) = a0 + a1(x - x0) + a2(x - x0)^2 + ...
where a0, a1, a2, ... are constants to be determined, and x0 is the ordinary point of the differential equation.
Next, we can find the coefficients of the power series by substituting the series solution into the differential equation and equating coefficients of like powers of (x-x0). This leads to a system of equations for the coefficients, which can be solved iteratively.
After finding the homogeneous solution, we can find a particular solution using a similar method. Assuming a particular solution of the form:
y(x) = u(x) + v(x)
where u(x) is a solution to the associated homogeneous equation, and v(x) is a particular solution to the nonhomogeneous equation, we can use the method of undetermined coefficients to find v(x). This involves assuming a form for v(x) based on the form of f(x), and then solving for its coefficients using the same technique as before.
Once we have found both the homogeneous and particular solutions, we can combine them to obtain the general solution to the nonhomogeneous differential equation.
Learn more about nonhomogeneous differential equation here
brainly.com/question/30876746
#SPJ4
HELP ME PLEASE I NEED TO TURN IN MY ASSIGNMENT NOW!!!!!!!!! 30 POINTSSS
SOLVE FOR Y
2y + 8 1/5 = 33
SOLVE FOR N
2n + 4 1/5 = 9
Answers
Therefore, y is equal to 12 2/5 and n is equal to 2 2/5 in the equation.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. An equation is typically written with an equal sign (=) between two expressions. Equations can involve various mathematical operations, such as addition, subtraction, multiplication, division, exponents, and logarithms. Solving an equation typically involves performing mathematical operations on both sides of the equation to isolate the variable (the unknown value) and find its value.
Here,
To solve for y in the equation 2y + 8 1/5 = 33, we can follow these steps:
Subtract 8 1/5 from both sides of the equation:
2y = 33 - 8 1/5
2y = 24 4/5
Divide both sides of the equation by 2:
y = (24 4/5) / 2
y = 12 2/5
Therefore, y is equal to 12 2/5.
To solve for n in the equation 2n + 4 1/5 = 9, we can follow these steps:
Subtract 4 1/5 from both sides of the equation:
2n = 9 - 4 1/5
2n = 4 4/5
Divide both sides of the equation by 2:
n = (4 4/5) / 2
n = 2 2/5
Therefore, n is equal to 2 2/5.
To know more about equation,
https://brainly.com/question/9312365
#SPJ1