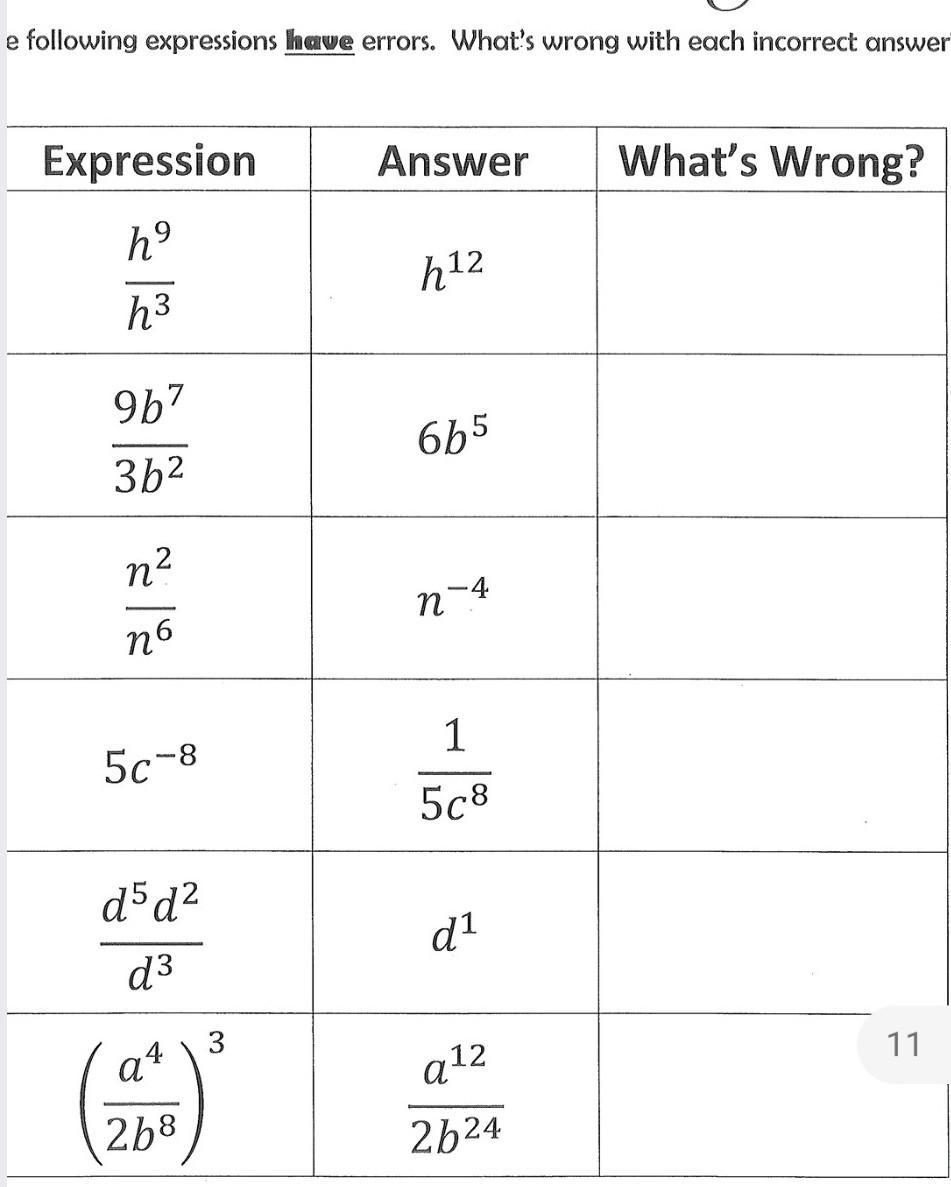
Answers
The incorrect expressions are given as follows:
h^9/h³ = h^6 -> keep the base and subtract the exponents.9b^7/3b² = 3b^5 -> we have to divide the bases.d^5 x d²/d³ = d^4 -> add the exponents in the numerator, then subtract the exponent with the denominator.How to simplify the exponential expressions?When two terms with the same base and different exponents are multiplied, we keep the base and add the exponents.
When two terms with the same base and different exponents are divided, we keep the base and subtract the exponents.
More can be learned about exponent rules at https://brainly.com/question/11975096
#SPJ1
Related Questions
Graph Y = 1/2x - 4 on the coordinate plane
Answers
The x-axis and y-axis are two parallel number lines that meet at (0, 0) to form the shape of the letter t.
Describe Coordinate Plane?Geometric objects and mathematical equations are represented on the coordinate plane, a two-dimensional graph. It is made up of the x-axis and y-axis, two parallel number lines that meet at the starting point (0, 0). The horizontal coordinate is represented by the x-axis, while the vertical coordinate is represented by the y-axis. They combine to create the Cartesian coordinate system.
Positive numbers are labelled to the right of the origin and negative values are labelled to the left of the origin on the x-axis. Positive numbers are written above the origin of the y-axis, and negative numbers are written below it. An ordered pair (x, y), where x denotes the horizontal coordinate and y denotes the vertical coordinate, is used to represent each point on the coordinate plane.
For graphing linear equations, quadratic equations, and other functions, the coordinate plane is a helpful tool. Additionally, it is employed to depict geometric forms like polygons, circles, and lines. The distance between two points, the slope of a line, and other significant features of mathematical objects can be calculated by graphing points on the coordinate plane. With applications in physics, engineering, economics, and computer science, the coordinate plane is a fundamental idea in mathematics.
The graph is shown below when y=1.
To know more about graph visit:
brainly.com/question/31090865
#SPJ1
Graph attached below,
The coordinates of the plane is
x y
1 -3.5
2 -3
4 -2
6 -1.
What is equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.
Here the given equation is y = [tex]\frac{1}{2}x-4[/tex].
Now put x= 1 then y = [tex]\frac{1}{2}\times1-4 =\frac{1-8}{2}=\frac{-7}{2}=-3.5[/tex]
Now put x=2 then [tex]y=\frac{1}{2}\times2-4=1-4=-3[/tex]
Now put x=4 then [tex]y=\frac{1}{2}\times4-4=2-4=-2[/tex]
Now put x=6 then [tex]y=\frac{1}{2}\times6-4=3-4=-1[/tex]
Then coordinates of the plane is
x y
1 -3.5
2 -3
4 -2
6 -1.
To learn more about equation refer the below link
https://brainly.com/question/29336774
#SPJ1
102, 107, 99, 102, 111, 95, 91
Mean
Mode
Median
Range
Answers
Answer:
mean: 101 (add all the numbers then divide by 7)
mode: 102 (the most frequent number in the set)
median: 102 (the number in the middle of the set)
range: 20 (the difference between the largest and smallest number)
Mean = 101
Mode = 102
Median = 102
Range = 20
MEAN: Add up all the numbers, then divide by how many numbers there are.
102 + 107 + 99 + 102 + 111 + 95 + 91 = 707
707 ÷ 7 = 101
MODE: Arrange all numbers in order from lowest to highest or highest to lowest and then count how many times each number appears in the set. The one that appears the most is the mode.
91,95,99,102,102,107,111
MEDIAN: Arrange the numbers from smallest to largest. If the amount of numbers is odd, the median is the middle number. If it is even, the median is the average of the two middle numbers in the list.
91,95,99,102,102,107,111
RANGE: Subtract the lowest number from the highest number
111 - 91 = 20
Please fill in all of the blanks
Answers
Answer:
The perimeter of this trapezoid is
7 + 5 + 3 + 7 + 4 = 26 cm
rectangle, A = lw, 4 × 7 = 28 square cm
triangle, A = (1/2)bh, (1/2) × 3 × 4 =
6 square cm
(1/2)(4)(7 + 10) = (1/2)(4)(17) = 34 square cm = 28 square cm + 6 square cm
This past semester, a professor had a small business calculus section. The students in the class were William comma Mike comma Allison comma Kristin comma Jim comma Neta comma Pam comma and Jinita. Suppose the professor randomly selects two people to go to the board to work problems. What is the probability that Neta is the first person chosen to go to the board and Jinita is the second?
Answers
The probability that Neta is chosen first and Jinita is chosen second is:
1/56(or approximately 0.018.)
There are 8 students in class, so there are 8 choices for first person and 7 choices for second person.
Since we want to calculate probability that Neta is chosen first and Jinita is chosen second, we need to consider the number of ways in which these two students can be chosen in that order.
There is only one way for Neta to be chosen first and Jinita to be chosen second, so the total number of possible outcomes is:
8 x 7 = 56
Therefore, the probability that Neta is chosen first and Jinita is chosen second is: 1/56 or approximately 0.018.
To know more about probability, here
brainly.com/question/30034780
#SPJ4
In a 10-kilometer race, there are no race
monitors for the first kilometer. After
that, there are race monitors every
0.25 kilometer, including at the finish
line. How many race monitors are there
Answers
Therefore, there are 37 race monitors in the entire 10-kilometer race.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It usually contains one or more variables, and the goal is to find the value of the variable(s) that satisfies the equation. An equation can be written in various forms, such as standard form, slope-intercept form, or general form, depending on the type of equation and the information given. Equations are used in many areas of mathematics, science, and engineering to model and solve problems.
Here,
There are race monitors every 0.25 kilometers, so we can divide the race into segments of 0.25 kilometers.
The first segment is from 1 kilometer to 1.25 kilometers. Since there are no monitors for the first kilometer, we only need to count the monitors from 1 kilometer to the finish line.
To find the number of monitors from 1 kilometer to the finish line, we can subtract 1 from the total distance of the race and then divide by 0.25 (since there is a monitor every 0.25 kilometers after the first kilometer):
(10 - 1) / 0.25 = 36
So there are 36 race monitors from 1 kilometer to the finish line. But since there are no monitors for the first kilometer, we need to add 1:
36 + 1 = 37
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
the ratio of a time a student spends on their art project to time spent on their science project is 3:4.The total amount of time the student spends on projects for these 56 min.How much does the students spend on projects for each subject
Answers
Answer: the student spends 24 minutes on their art project and 32 minutes on their science project.
Step-by-step explanation:
Answer:
The student spends 24 minutes on their art project, and 32 minutes on their science project
Step-by-step explanation:
To solve this problem, we can utilise the unitary method, a process by which we find the value of a single unit, from the value of multiple units and thus, the value of multiple units from the value of a single unit.
If the total number of units in the ratio is (3+4)=7, then 7 units = 56 mins.
If 7 units = 56 mins,
then 1 unit = 56/7 mins = 8 mins.
Therefore, 3 units = 8×3 = 24 mins,
and 4 units = 8×4 = 32 mins.
Thus, the student spends 24 minutes on their art project, and 32 minutes on their science project
HELP MARKING BRAINLEIST
Answers
Answer:
r = 2
center: ( -7,0 )
Step-by-step explanation:
5 × (10 + 7) = (5 × 10) + (5 ×7)
Answers
Answer:
Same equation just using the assocaitive property
Step-by-step explanation:
For example, 8 + (2 + 3) = (8 + 2) + 3 = 13
Hope this helps! =D
Select the correct answer. Sides of three square rooms measure 14 feet each, and sides of two square rooms measure 17 feet each. Which expression shows the total area of these five rooms? A. (3 × 14^2) + (2 × 17^2) B. (2 × 14^3) + (2 × 17^2) C. (3 × 17^2) + (2 × 14^2) D. (3 × 14^2) × (2 × 17^2) Reset Next
Answers
The correct expression showing the total area of the five rooms is A. (3 x 14²) + (2 x 17²), which simplifies to 1918 square feet.
What is expression?An expression is a combination of numbers, symbols, and operators (such as addition, subtraction, multiplication, and division) that represent a mathematical calculation. An expression can be a single number, a variable, or a combination of both, and can be used to represent mathematical formulas, equations, or relationships.
In the given question,
C. (3 × 17²) + (2 × 14²)
To find the total area of the five rooms, we need to add the area of each room. The area of a square is found by squaring the length of one side.
For the three rooms with sides of 14 feet each, the area of each room is:
14^2 = 196 square feet
So the total area of these three rooms is:
3 × 196 = 588 square feet
For the two rooms with sides of 17 feet each, the area of each room is:
17^2 = 289 square feet
So the total area of these two rooms is:
2 × 289 = 578 square feet
Therefore, the total area of all five rooms is:
588 + 578 = 1166 square feet
Option C, (3 × 17²) + (2 × 14²), gives the correct expression for this calculation.
To know more about expression, visit:
https://brainly.com/question/2559684
#SPJ1
Write the equation of the line that passes through the point (0, 4) and is parallel to the line with equation y=5x+3
Answers
Sorry if my english is a bit weird, i hope that helped!
the quality control manager at a computer manufacturing company believes that the mean life of a computer is 80 months, with a variance of 64 . if he is correct, what is the probability that the mean of a sample of 77 computers would be greater than 82.59 months? round your answer to four decimal places.
Answers
The probability that the mean of a sample of 77 computers would be greater than 82.59 months, assuming the population mean is 80 months and the variance is 64, is approximately 0.0606
The situation described can be modeled using a normal distribution, with a mean of 80 months and a standard deviation of the square root of the variance, which is 8 months (since variance = standard deviation squared).
To find the probability that the mean of a sample of 77 computers would be greater than 82.59 months, we need to standardize the sample mean using the formula
z = (x - μ) / (σ / √n)
where
x is the sample mean
μ is the population mean (believed to be 80 months)
σ is the population standard deviation (8 months)
n is the sample size (77)
Plugging in the values, we get
z = (82.59 - 80) / (8 / √77) ≈ 1.55
To find the probability of a z-score being greater than 1.55, we can use a standard normal distribution table or calculator. From the table, we find that the probability of z being greater than 1.55 is approximately 0.0606.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
write an integral that quantifies the change in the area of the surface of a cube when its side length quadruples from s unit to 4s units.
Answers
Answer:
Step-by-step explanation:
Let A be the area of the surface of the cube.
When the side length changes from s to 4s, the new area A' can be calculated as:
A' = 6(4s)^2 = 96s^2
The change in area is then:
ΔA = A' - A = 96s^2 - 6s^2 = 90s^2
To find the integral that quantifies the change in area, we can integrate the expression for ΔA with respect to s, from s to 4s:
∫(90s^2)ds from s to 4s
= [30s^3] from s to 4s
= 30(4s)^3 - 30s^3
= 1920s^3 - 30s^3
= 1890s^3
Therefore, the integral that quantifies the change in area of the surface of a cube when its side length quadruples from s units to 4s units is:
∫(90s^2)ds from s to 4s
= 1890s^3 from s to 4s
= 1890(4s)^3 - 1890s^3
= 477,840s^3 - 1890s^3
Alfred buys a car for £13960 which depreciates in value at a rate of 0.75% per year.
Work out how much Alfred's car will be worth in 12 years.
Answers
Answer:
£12063.57
Step-by-step explanation:
The value of Alfred’s car after 12 years can be calculated using the formula for exponential decay: Final Value = Initial Value * (1 - rate of depreciation)^(number of years). Plugging in the values we get: Final Value = 13960 * (1 - 0.0075)^12. Therefore, after 12 years, Alfred’s car will be worth approximately £12063.57.
Two 5-year old girls, Alyse and Jocelyn, have been training to run a 1 mile race. Alyse’s 1 mile time A is approximately Normally distributed with a mean of 13. 5 minutes and a standard deviation of 2. 5 minutes.
Jocelyn’s 1 mile time J is approximately Normally distributed with a mean of 12 minutes and a standard deviation of 1. 5 minutes.
Assuming A and J are independent random variables, what is the probability that
Alyse has a smaller time than Jocelyn in a 1 mile race on a randomly selected day?
I'm more so looking for an explanation on how to find the answer, thanks :)
Answers
The probability that Alyse has a smaller time than Jocelyn in a 1 mile race on a randomly selected day is approximately 0.2676
To find the probability that Alyse has a smaller time than Jocelyn in a 1 mile race on a randomly selected day, we need to compare the distribution of their running times.
Let X be the running time of Alyse and Y be the running time of Jocelyn. Then, we have
X ~ N(13.5, 2.5^2)
Y ~ N(12, 1.5^2)
We want to find P(X < Y). We can start by standardizing the variables:
Zx = (X - 13.5) / 2.5
Zy = (Y - 12) / 1.5
Then, we have
P(X < Y) = P(X - Y < 0)
Substituting the standardized variables, we get
P(X - Y < 0) = P((Zx - Zy) < (0 - (13.5-12)/sqrt(2.5^2 + 1.5^2)))
Using the standard Normal distribution table or calculator, we find that the probability of Zx - Zy being less than -0.624 is approximately 0.2676.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Arun has 72 coins. He has 5-cent and 10-cent coins in the ratio 5: 3.
Arun said: I have just over
$5 in total.
Is Arun correct? Explain your answer. Show your working.
Answers
Arun is not correct - he has just under $5 in total, not just over.
How to determine how much Arun has in totalLet's start by finding out how many 5-cent and 10-cent coins Arun has.
Let the number of 5-cent coins be 5x and the number of 10-cent coins be 3x (since the coins are in the ratio 5:3).
Then the total value of the 5-cent coins is 5x0.05 = 0.25x dollars, and the total value of the 10-cent coins is 3x0.1 = 0.3x dollars.
So the total value of all the coins is 0.25x + 0.3x = 0.55x dollars.
Since Arun has 72 coins, we know that 5x + 3x = 72, or 8x = 72, or x = 9.
Therefore, Arun has 5x = 59 = 45 5-cent coins and 3x = 39 = 27 10-cent coins.
The total value of these coins is 450.05 + 270.1 = 2.25 + 2.7 = 4.95 dollars.
So Arun is not correct - he has just under $5 in total, not just over.
Learn more about total value at https://brainly.com/question/25109150
#SPJ1
what minus 1 1/2 equals 3 3/4
Answers
Answer:
5 1/4
Step-by-step explanation:
Here is a bank statement.
=
$
Responsible Bank
210 2nd Street
Anytown, MH 06930
Andre Person
1729 Euclid Ave
Anytown, MH 06930
Date
2017-10-03 Previous Balance
2017-10-05 Check Number 256
2017-10-06 ATM Deposit - Cash
2017-10-10 Wire Transfer
2017-10-17 Point of Sale - Grocery Store
2017-10-25 Funds Transfer from Savings
2017-10-28 Check Number 257
2017-10-29 Online Payment - Phone Services
Description
Checking Account Statement
Page: 1 of 1
Statement Period
2017-10-01 to 2017-11-01
Withdrawals Deposits
28.50
37.91
16.43
42.00
72.50
45.00
50.00
1. If we put withdrawals and deposits in the same column, how can they be represented?
2. Andre withdraws $40 to buy a music player. What is his new balance?
3. If Andre deposits $100 in this account, will he still be in debt? How do you know?
Account No.
1120635978
Balance
39.87
11.37
56.37
18.46
2.03
52.03
10.03
-62.47
Answers
The analysis of the bank statement thus, given below. Since the result is negative, this means that Andre would still have a negative balance after depositing $100, and therefore would still be in debt.
What is bank statement analysis?1. If we put withdrawals and deposits in the same column, they can be represented as positive and negative values in a single column. Deposits would be represented with positive values, and withdrawals would be represented with negative values.
2. Andre's new balance would be $16.37. We can calculate this by subtracting $40 (the withdrawal) from his previous balance of $56.37:
$56.37 - $40 = $16.37
3. If Andre deposits $100 in this account, he will no longer be in debt. We can calculate his new balance by adding his previous balance and the deposit, and then subtracting any withdrawals:
$56.37 + $100 = $156.37 (balance after the deposit)
$156.37 - $28.50 - $37.91 - $16.43 - $42.00 - $72.50 - $45.00 - $50.00 - $10.03 - $62.47 = -$49.47
Since the result is negative, this means that Andre would still have a negative balance after depositing $100, and therefore would still be in debt.
Learn more about bank statement at:
https://brainly.com/question/22786262
#SPJ1
I don’t know what to write for the equation.
Answers
fraction wise, a whole is always simplified to 1, so
[tex]\cfrac{4}{4}\implies \cfrac{1000}{1000}\implies \cfrac{9999}{9999}\implies \cfrac{17}{17}\implies \text{\LARGE 1} ~~ whole[/tex]
so, we can say the whole of the players, namely all of them, expressed in fourth is well, 4/4, that's the whole lot, and we also know that 3/4 of that is 12, the guys who chose the bottle of water
[tex]\begin{array}{ccll} fraction&value\\ \cline{1-2} \frac{4}{4}&p\\[1em] \frac{3}{4}&12 \end{array}\implies \cfrac{~~ \frac{4 }{4 } ~~}{\frac{3}{4}}~~ = ~~\cfrac{p}{12}\implies \cfrac{~~ 1 ~~}{\frac{3}{4}} = \cfrac{p}{12}\implies \cfrac{4}{3}=\cfrac{p}{12} \\\\\\ (4)(12)=3p\implies \cfrac{(4)(12)}{3}=p\implies 16=p[/tex]
An analyst is interested in testing the hypothesis that stock betas are higher in a down market (when the market index returns are negative) than otherwise.
Write the regression equation you would employ to test the analyst’s hypothesis.
Answers
This supports the analyst's hypothesis that betas are higher in down markets.
What is the meaning of equations?In algebra, the definition of an equation, in its simplest form, is a mathematical statement that shows that two mathematical expressions are equal. For example, 3x + 5 = 14 is an equation where 3x + 5 and 14 are two expressions separated by the equation.
To test the hypothesis that stock betas are higher in bear markets, we use the following regression equation:
Ri = αi + βi(Rm) + εi
where,
Ri = return on ith stock
Rm = market return
αi = intercept (constant term) of the regression equation of the ith stock.
βi = slope of the market return of the ith stock (regression coefficient).
εi = error period of the ith stock
To test the hypothesis, we include an additional variable in the regression equation that describes the effect of the market return when it is negative. This variable would be a dummy variable that takes the value 1 if the market return is negative and 0 otherwise. Let's call this variable D. So the modified regression equation would be:
Ri = αi + βi(Rm) + γiD + εi
where,
γi = the excess regression coefficient of the ith stock that describes the effect of the market return when it is negative
The coefficient γi measures the difference between the beta value of a stock between a falling market and a non-falling market. If γi is significantly greater than 0, this supports the analyst's hypothesis that betas are higher in down markets.
Learn more about algebra here
https://brainly.com/question/24875240
#SPJ1
A student was asked to form different triangles with angle measures of 90 degrees, 30 degrees, and 60 degrees. She incorrectly said this triangle is the only triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees. What mistake might she have made
Answers
The student's mistake might have been that she assumed that there is only one possible triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees. However, this is not true.
what is triangle ?
A triangle is a three-sided polygon, which is a closed two-dimensional shape with straight sides. It is one of the basic shapes in geometry and is used in various fields such as mathematics, physics, engineering, and architecture.
In the given question,
The student's mistake might have been that she assumed that there is only one possible triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees. However, this is not true. In fact, there are infinitely many triangles with these angle measures, since the length of the sides can vary.
The most well-known triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees is the 30-60-90 triangle, which has specific side ratios of 1:sqrt(3):2. But this is just one possible example of a triangle with those angle measures, and it is not the only one.
It is important to note that in a triangle, the angles determine the shape and the side lengths determine the size. Therefore, if two triangles have the same angle measures, they will be similar, but they may not necessarily be congruent unless they also have the same side lengths.
To know more about triangle , visit:
https://brainly.com/question/2773823
#SPJ1
Using the graph, determine the equation of the axis of symmetry.
Answers
Step-by-step explanation:
x = -4 ( the value of the x-coordinate of the vertex is the axis of symmetry for normal up or down opening parabolas)
Please please help me!!
see the attached item for more information
Answers
Answer:
Set your calculator to degree mode.
[tex] \tan(39) = \frac{12}{x} [/tex]
[tex]x \tan(39) = 12[/tex]
[tex]x = \frac{12}{ \tan(39) } = 14.818766[/tex]
So the area of this triangle is
(1/2)(14.818766)(12) = 88.91 (B)
help please without guessing ?//
Answers
Answer:
D. y ≥ x² - 4x - 5
Step-by-step explanation:
We can observe two characteristics of this graphed inequality:
1. its shading is above it, therefore the inequality sign must be greater than
2. its boundary line is continuous, not dotted, so the inequality sign must include or equal to
From these two observations, we can assert that D. x² - 4x - 5 is the correct answer because it is the only one which has a greater than or equal to sign.
____________
Note:
We can also check that the equation for the inequality is correct by converting it to vertex form by completing the square, then graphing it ourselves:
[tex]y \ge (x-2)^2 - 9[/tex]
Answer:
The answer is y≥ x²-4x-5
Step-by-step explanation:
x=a,x=b
where a,b are roots of the equation
a= -1 b=5
x= -1,x=5
x+1=0,x-5=0
(x+1)(x-5)=0
x²-5x+x-5=0
x²-4x-5=0
April is considering a 7/23 balloon mortgage with an interest rate of 4.15% to
purchase a house for $197,000. What will be her balloon payment at the end
of 7 years?
OA. $173,819.97
OB. $170,118.49
OC. $225,368.29
OD. $170,245.98
SUBMIT
Answers
The balloon payment at the end of 7 years would be $173,819.97, which is option A.
How to find the balloon payment at the end of 7 yearsA 7/23 balloon mortgage means that April will make payments on the loan as if it were a 23-year mortgage, but the remaining balance of the loan will be due in full after 7 years.
To find the balloon payment at the end of 7 years, we can first calculate the monthly payment using the loan amount, interest rate, and loan term:
n = 23 * 12 = 276 (total number of payments)
r = 4.15% / 12 = 0.003458 (monthly interest rate)
P = (r * PV) / (1 - (1 + r)^(-n))
where
PV is the present value of the loan (the loan amount)n is the total number of paymentsr is the monthly interest ratePV = $197,000
P = (0.003458 * $197,000) / (1 - (1 + 0.003458)^(-276)) = $1,007.14 (monthly payment)
Now we can calculate the remaining balance on the loan after 7 years. Since April is making payments as if it were a 23-year mortgage, she will have made 7 * 12 = 84 payments by the end of the 7th year.
Using the formula for the remaining balance of a loan after t payments:
B = PV * (1 + r)^t - (P / r) * ((1 + r)^t - 1)
Where
B is the remaining balancePV is the initial loan amount r is the monthly interest rateP is the monthly payment t is the number of payments madet = 84 (number of payments made)
B = $197,000 * (1 + 0.003458)^84 - ($1,007.14 / 0.003458) * ((1 + 0.003458)^84 - 1)
B = $173,819.97
Therefore, the balloon payment at the end of 7 years would be $173,819.97, which is option A.
Learn more about monthly payment here : brainly.com/question/28106777
#SPJ1
Quadrilateral ABCD has vertices A = (2, 5), B = (2, 2), C = (4, 3) and D = (4, 6). Quadrilateral A'B'C'D' is formed when Quadrilateral ABCD is dilated by a scale factor of 2. Which statement is true? Select all that apply
Choose all that apply:
A) None of the answers apply
B) The angles of Quadrilateral ABCD and Quadrilateral A'B'C'D' are the same.
C) The side lengths of Quadrilateral ABCD and Quadrilateral A'B'C'D' are the same.
Answers
The statement which is true for the quadrilateral is B.
How to determine which statements are true for the quadrilateral?To dilate a figure by a scale factor of 2, each point of the original figure is multiplied by 2.
So the coordinates of each vertex of A'B'C'D' are twice the coordinates of the corresponding vertex of ABCD.
The coordinates of A' are (4,10), B' are (4,4), C' are (8,6), and D' are (8,12).
To determine which statements are true, we can compare the angles and side lengths of the two quadrilaterals:
A) None of the answers apply. This may be a valid answer, but we should check the other options before concluding that none of them apply.
B) The angles of Quadrilateral ABCD and Quadrilateral A'B'C'D' are the same. This is true because dilation does not change angles. The corresponding angles of the two quadrilaterals are congruent.
C) The side lengths of Quadrilateral ABCD and Quadrilateral A'B'C'D' are not the same. We can see this by calculating the length of each side of both quadrilaterals.
Therefore, the correct answer is B.
Learn more about Quadrilateral on:
https://brainly.com/question/23935806
#SPJ1
If you watch from ground level, a child riding on a merry-go-round will seem to be undergoing simple harmonic motion from side to side. Assume the merry-go-round is 10.6 feet across and the child completes 8 rotations in 120 seconds. Write a sine function that describes d, the child's apparent distance from the center of the merry-go-round, as a function of time t.
Answers
The sine function that describes the child's apparent distance from the center of the merry-go-round is d(t) = 5.3 sin(2π/15 * t)
How to write a sine function that describes the child's apparent distance?To write a sine function that describes the child's apparent distance from the center of the merry-go-round as a function of time t, we can start by finding the amplitude, period, and phase shift of the motion.
Amplitude:
The amplitude of the motion is half the diameter of the merry-go-round, which is 10.6/2 = 5.3 feet. This is because the child moves back and forth across the diameter of the merry-go-round.
Period:
The period of the motion is the time it takes for the child to complete one full cycle of back-and-forth motion, which is equal to the time it takes for the merry-go-round to complete one full rotation.
From the given information, the child completes 8 rotations in 120 seconds, so the period is T = 120/8 = 15 seconds.
Phase shift:
The phase shift of the motion is the amount of time by which the sine function is shifted horizontally (to the right or left).
In this case, the child starts at one end of the diameter and moves to the other end, so the sine function starts at its maximum value when t = 0. Thus, the phase shift is 0.
With these values, we can write the sine function that describes the child's apparent distance from the center of the merry-go-round as:
d(t) = 5.3 sin(2π/15 * t)
where d is the child's distance from the center of the merry-go-round in feet, and t is the time in seconds. The factor 2π/15 is the angular frequency of the motion, which is equal to 2π/T.
Learn more about sine function on:
https://brainly.com/question/30243373
#SPJ1
When x is 2, what is the value of the expression 124+3(8−x)12
12
4
+
3
(
8
−
x
)
12
?
Answers
When x is 2, the value of the expression is 9.
Describe Algebraic Expression?An algebraic expression is a mathematical phrase that contains one or more variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. It can also contain exponents, roots, and trigonometric functions.
Algebraic expressions are used to represent mathematical relationships and solve problems in a wide range of fields, including physics, engineering, finance, and statistics. They can be used to model real-world phenomena and to make predictions based on data.
Algebraic expressions can be simplified by combining like terms and using mathematical rules and properties. They can also be evaluated by substituting values for the variables and simplifying the expression. Solving equations involving algebraic expressions often involves manipulating the expression to isolate a variable and find its value.
When x is 2, the value of the expression 12/4+3(8−x)-12 can be found by substituting 2 for x and simplifying the expression:
12/4 + 3(8 - 2) - 12
= 3 + 3(6) - 12
= 3 + 18 - 12
= 9
Therefore, when x is 2, the value of the expression is 9.
To know more about expression visit:
https://brainly.com/question/15813344
#SPJ1
The complete question is :
When x is 2, what is the value of the expression 12/4+3(8−x)-12?
The radius of a basketball is about 13 centimeters.
What is the volume of the basketball?
Answers
Answer:
The answer that you're looking for is approximately 9202.77 and in terms of π it is 2929.33π
Step-by-step explanation:
Using the equation [tex]\frac{4}{3}\pi r^{3}[/tex] you can replace r with 13 to get [tex]\frac{4}{3} \pi 13^{3}[/tex] you then multiply them all to get 9202.77 and divide by π to find the terms of pi which is 2929.33π.
I hope this was helpful!
Solve for X, please write an explanation.
Answers
Step-by-step explanation:
2x+20 and 2x-4 are supplementary angles...they form a straight line and thus = 180 degrees when added together
2x+20 + 2x-4 = 180 simplify
4x + 16 = 180 subtract 16 from both sides
4x = 164 divide both sides by 4
x = 41 degrees
we will eventually see using the theory of taylor series that can be computed using an infinite series: which convergence test shows that the series does in fact converge?
Answers
A number of
convergence tests
can be used to examine a Taylor series' convergence, but the Ratio Test is one that is frequently employed. According to the
ratio test, the series converges absolutely if the limit of the
absolute value
of the ratio of the (n+1)th term to the nth term is smaller than 1. In mathematics, this is expressed as:
lim┬(n→∞)〖|a_(n+1)/a_n |<1〗
where a n is the
series' nth term. The series
diverges
if the limit is bigger than 1, and extra tests must be employed if the limit is equal to 1.
Although the
Ratio Test
is a frequently used test for
Taylor series
convergence, it is not always appropriate and other tests can be required based on the unique characteristics of the series.
Learn more about
Taylor series
:
https://brainly.com/question/28158012
#SPJ4