HELLO PLEASE HELP!
i only need help with the second problem which is:

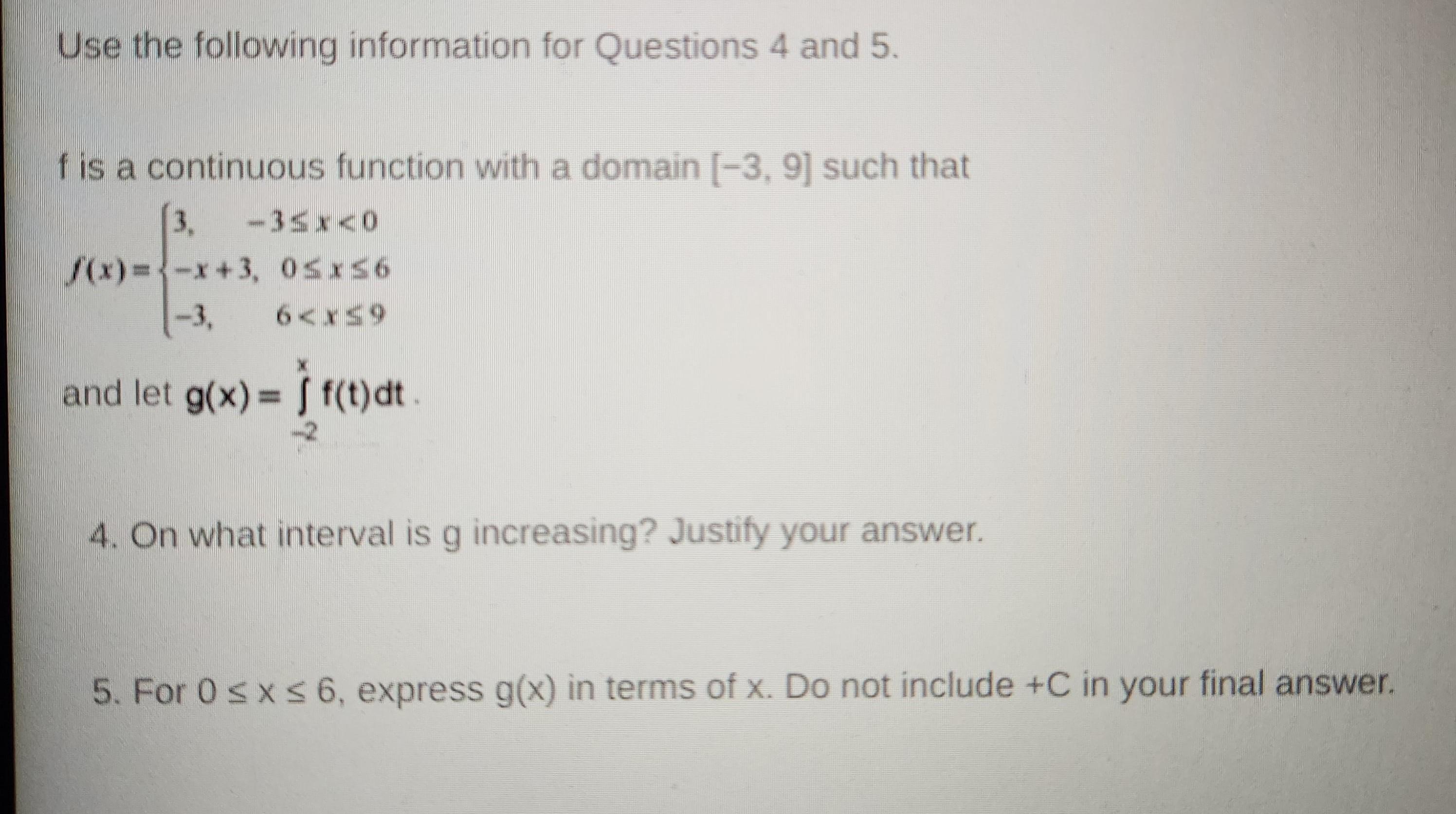
5. For 0≤x≤ 6, express g(x) in terms of x. Do not include +C in your final answer.

please and thanks!​

Answer:

21.8 - 0.1 = 21.7

21.7 is 0.1 less than 21.8

Answer:

The answer is 21.7

Step explanation

21.8 - 0.1 = 21.7

I hope it helped you.

Please Mark me brainliest

The probability is 35/1296, or approximately 0.027 or 2.7%.

What is the probability?

Probability is the study of the chances of occurrence of a result, which are obtained by the ratio between favorable cases and possible cases.

The total number of outcomes when rolling a pair of dice is 36 (since each die has 6 faces and can result in 6 possible outcomes).

To find the probability of the first roll resulting in a total of at least 3, we need to determine the favorable outcomes. The only combination that does not result in a total of at least 3 is when both dice show a 1, which is only one possible outcome. So, there are 35 favorable outcomes (36 total outcomes - 1 unfavorable outcome) for the first roll.

To find the probability of the second roll resulting in a total of at least 12, we need to determine the favorable outcomes. The only combination that results in a total of 12 is when both dice show a 6, which is only one possible outcome. So, there is only 1 favorable outcome for the second roll.

Therefore, the probability of the first roll resulting in a total of at least 3 and the second roll resulting in a total of at least 12 is:

(35/36) * (1/36) = 35/1296

Hence, the probability is 35/1296, or approximately 0.027 or 2.7%.

To learn more about probability, Visit

https://brainly.com/question/13604758

#SPJ1

Answer:

A = 50.24 m²

Step-by-step explanation:

A = π r²

d = 8 m

r = d/2

r = 8/2

r = 4 m

A = 3.14 × (4)² m

A = 3.14 × 16 m

A = 50.24 m²

Answer:

50.24 m²

Step-by-step explanation:

Diameter = 8 m

Formula

Radius ( r ) = Diameter/2

r = 8/2

r = 4 m

Formula

Area of circle = π r²

Note

The value of π is 3.14 ( approximately )

Area of circle

= 3.14 × 4²

= 3.14 × 4 × 4

= 3.14 × 16

= 50.24 m²

Hence,

The area of circle is 50.24 m².

We can prove that if there exists a walk of odd length starting and ending at vertex v in a graph G, then there must exist an odd cycle that does not repeat any vertices.

what is  vertex ?

In mathematics, a vertex is a point where two or more lines, curves, or edges meet. It is a common term used in geometry, graph theory, and other areas of mathematics.

In the given question,

We can prove that if there exists a walk of odd length starting and ending at vertex v in a graph G, then there must exist an odd cycle that does not repeat any vertices.

To see why, suppose there exists a walk w of odd length starting and ending at v, and suppose w is the shortest such walk. If w does not repeat any vertices, then we have found an odd cycle that does not repeat any vertices, and we are done.

Suppose instead that w repeats some vertex v' (not equal to v). Then we can split w into two walks, w1 and w2, where w1 starts at v, goes to v', and then returns to v, and w2 is the rest of w starting and ending at v'. Since v' is not equal to v, both w1 and w2 are walks of odd length, and both are strictly shorter than w. By the minimality of w, both w1 and w2 must contain odd cycles that do not repeat any vertices. We can then combine these cycles to form an odd cycle that does not repeat any vertices in G, and we are done.

To know more about  vertex , visit:

https://brainly.com/question/30940247

#SPJ1

The statements that are always true regarding the given diagram of the triangle are m∠2 + m∠3 = m∠6, m∠3 + m∠4 + m∠5 = 180°, m∠5 + m∠6 = 180°. Therefore, options (4) and (5) are not always true.

An exterior angle of a polygon is an angle that forms a linear pair with an interior angle of the polygon. In other words, it is an angle formed by extending one of the sides of the polygon. For any given vertex of the polygon, the exterior angle is the angle between a line containing the side of the polygon next to the vertex and a line that is an extension of the adjacent side. The measure of an exterior angle is equal to the sum of the measures of its corresponding remote interior angles (interior angles that are not adjacent to the exterior angle). The sum of the exterior angles of any polygon, including a triangle, is always equal to 360 degrees. Exterior angles are used in a variety of geometric proofs and constructions.

We know that the sum of all the interior angles of any triangle is 180 degrees. Therefore, we can use this fact to determine which statements are always true regarding the given diagram.

Now, we can use the following relationships between the interior and exterior angles of a triangle:

Exterior angle = Sum of interior angles adjacent to it

Interior angle = 180  - Exterior angle

Using these relationships, we can determine which statements are always true:

m∠5 + m∠3 = m∠4: This is true because the exterior angle at angle 3 is equal to the sum of angles 3 and 4, and the exterior angle at angle 5 is equal to the sum of angles 5 and 6. Therefore, m∠5 + m∠3 + m∠6 = m∠4 + m∠3, which simplifies to m∠5 + m∠3 = m∠4.

Given m∠3 + m∠4 + m∠5 = 180°: This is true because the sum of all the interior angles of a triangle is 180 degrees.

m∠5 + m∠6 = 180°: This is not always true because sum of all the angles should be 180. It is true in this specific case because angle 1 is a straight angle, which means that m∠5 + m∠6 = 180°. However, in general, this statement is not always true.

m∠2 + m∠3 = m∠6: This is true because the exterior angle at angle 2 is equal to the sum of angles 2 and 6. Therefore, m∠2 + m∠3 = m∠6.

Given m∠2 + m∠3 + m∠5 = 180°: This is may not always true. It is true in this specific case because angle 1 is a straight angle, which means that m∠2 + m∠3 + m∠5 = 180°. However, in general, this statement is not always true.

Therefore, the three statements that are always true from the diagram are:

m∠5 + m∠3 = m∠4

m∠3 + m∠4 + m∠5 = 180°

m∠2 + m∠3 = m∠6

To know more about exterior angles visit:

brainly.com/question/28835566

#SPJ1

Based on the information given, we can use the Pythagorean theorem to determine the distance traveled by the northbound car.

Let's denote the distance traveled by the northbound car as 'x' kilometers.

According to the Pythagorean theorem, in a right triangle, the square of the hypotenuse (the straight-line distance between the two cars) is equal to the sum of the squares of the other two sides (the distances traveled by each car).

In this case, the northbound car's distance is 'x' kilometers and the eastbound car's distance is 5 kilometers.

So we have the equation:

x^2 + 5^2 = 13^2

Simplifying, we get:

x^2 + 25 = 169

Subtracting 25 from both sides, we get:

x^2 = 144

Taking the square root of both sides, we get:

x = 12

So the northbound car has traveled 12 kilometers.

Answer: 12 km

Step-by-step explanation:

As seen in the figure the distance that the northbound car traveled equals to the distance from point N to the parking lot.

pythagorean: [tex]\sqrt{13^{2}-5^{2} }=12km[/tex]

Answer: you need to add

Step-by-step explanation: I would ask your teacher to help you understand the lesson.  

subtract 3 from both sides to get

4x > 27

divide both sides by 4 to get

x > 27/4 or 6 3/4

Therefore, the correct response From these integral is option D   is.  

``` 10 + ∫₅¹  R(t) dt

An integral is a mathematical construct in mathematics that can be used to represent an area or a generalization of an area. It computes volumes, areas, and their generalizations. Computing an integral is the process of integration.

Integration can be used, for instance, to determine the area under a curve connecting two points on a graph. The integral of the rate function R(t) with respect to time t can be used to describe how much water is present in a tank.

The following equation can be used to determine how much water is in the tank at time t = 5 if there are 10 gallons of water in the tank at time t = 1.

``` 10 + ∫₅¹  R(t) dt

To know more about integral visit:

brainly.com/question/30900582

#SPJ1

Answer:

Let's start by writing the given statement as an equation.

Twice the sum of −4 and a number is the same as the number decreased by 5/2:

2(-4 + x) = x - 5/2

Where x represents the unknown number.

Now, let's simplify and solve for x:

-8 + 2x = x - 5/2

Adding 8 and 5/2 to both sides, we get:

2x + 8.5/2 = x + 1.5/2

Simplifying, we get:

2x + 17/2 = x + 3/2

Subtracting x and 3/2 from both sides, we get:

x + 17/2 = 3/2

Subtracting 17/2 from both sides, we get:

x = -7

Therefore, the number is -7.

To check our answer, we can substitute x = -7 into the original equation:

2(-4 + (-7)) = (-7) - 5/2

-2 = -2.5

The left-hand side does not equal the right-hand side, so our solution is incorrect. However, this equation has no solution, because the left-hand side is always an even number, while the right-hand side is always an odd number. Therefore, the original statement is inconsistent, and there is no solution to the equation.

The probability that a person who tests positive actually has the disease is ≈0.0158.

        Probability is a way to gauge how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about the likelihood of an event happening, or how likely it is. Probability can range from 0 to 1, with 0 denoting an impossibility and 1 denoting a certainty. 1 is the probability of every event in a sample space.

    For instance, when we flip a coin, there are just two possible results: Head OR Tail. (H, T). However, if two coins are tossed, there are four possible results: (H, H), (H, T), (T, H), and (T, T).

we solve the given question using BAYE's theorem:

Bayes' Theorem states that the conditional probability of an event, based on the occurrence of another event, is equal to the likelihood of the second event given the first event multiplied by the probability of the first event.

P(disease/positive)= [tex]\frac{P(disease)P(positive/disease)}{P(disease)P(positive/disease)+P(no disease)P(positive/disease)}[/tex]

P(disease/positive)= [tex]\frac{(0.008)(0.04)}{(0.008)(0.04)+(0.992)(0.02)}[/tex]  ≈ 0.0158

To know more about Bayes' Theorem visit:

brainly.com/question/29598596

#SPJ1

The mean score is 628.

What is mean?

In statistics, the mean is a measure of central tendency, which represents the average value of a data set. It is also known as the arithmetic mean and is calculated by adding up all the values in the data set and then dividing by the number of observations in the data set. The formula for calculating the mean is:

mean = (sum of all values) / (number of observations)

Now,

To find the mean score, you need to add up the three scores and then divide by 3:

(650 + 600 + 635) / 3 = 628.33

Rounding to the nearest whole point, the mean score is 628.

To know more about Mean visit the link

brainly.com/question/30112112

#SPJ1

As a result, the square's sides measure about **6.08 cm** in length.

The following formula is used to determine a square's area:

Area = side² is a formula.

where "side" denotes the measurement of one of the square's sides.

Assume for the moment that the two squares have sides that are 'x' and 'y' long. We are aware that a square's area is equal to the square of one of its sides. Consequently, using the above data, we can create the following two equations:

``` x² + y² = 74   (Equation 1)

The second equation is x = y.

Equation 2 can be entered in place of Equation 1 to yield:

2x² = 74,

x² = 37, and

x = √(37)

= 6.08, respectively.

To know more about side of square visit:

brainly.com/question/24584437

#SPJ1

Therefore, the correct answer is A. Y intercept will be less and X will be less.

A graph is a visual representation of data that shows the relationship between two or more variables. Graphs are commonly used to display information in a way that is easy to interpret and analyze. They are often used in fields such as science, mathematics, economics, and engineering to help illustrate and explain complex data.

Here,

The introduction of a cost of 0.25 cents per mile for the driver would be an additional expense for the trucking company, and would affect their profit. This means that the profit values (on the y-axis) would decrease for each point on the graph. However, the miles traveled (on the x-axis) would remain the same as the cost of the driver is proportional to the distance traveled.

Therefore, the y-intercept of the graph (the profit when the truck has traveled zero miles) would be less than it was before, because the trucking company has a new cost that reduces their overall profit. However, the x-intercept (the point where the profit is zero) would remain the same, as this point is determined solely by the revenue and cost of the trucking company.

The slope of the graph would also be affected, as the profit now decreases at a faster rate as the miles traveled increase. The new slope would depend on the specific values of the revenue, costs, and driver expenses for the trucking company, but in general, it would be steeper than before.

To know more about graph,

https://brainly.com/question/30934484

#SPJ1

Answer:

A) $2510

B) $209.17

C) $128,273.36

Step-by-step explanation:

Let's break this problem down into three parts:

a) To find out how much will be saved each year, we first need to calculate the annual salary and then determine 10% of it. Since the newscaster earns $25,100, we can calculate the annual savings as follows:

Annual savings = Annual salary * 10%

Annual savings = $25,100 * 0.1

Annual savings = $2,510

So, the newscaster will save $2,510 each year.

b) To find the monthly deposit, we need to divide the annual savings by the number of months in a year:

Monthly deposit = Annual savings / 12

Monthly deposit = $2,510 / 12

Monthly deposit ≈ $209.17

The newscaster will deposit approximately $209.17 per month into the retirement account.

c) To find the amount in the account after 29 years, we will use the formula for the future value of an ordinary annuity, since the investment has a monthly deposit and a monthly compounding interest rate:

FV = P * [(1 + r)^nt - 1] / r

Where FV is the future value, P is the monthly deposit, r is the monthly interest rate (annual interest rate divided by 12), n is the number of times interest is compounded per year (monthly, so 12), and t is the number of years.

In this case, P = $209.17, r = 4.1%/12, n = 12, and t = 29 years.

First, convert the annual interest rate to a decimal and then find the monthly interest rate:

Monthly interest rate = (4.1%/12) / 100

Monthly interest rate = (0.041/12)

Now, plug the values into the formula:

FV = $209.17 * [(1 + 0.041/12)^(12*29) - 1] / (0.041/12)

Calculate the future value:

FV ≈ $209.17 * [(1.003417)^(348) - 1] / (0.003417)

FV ≈ $209.17 * (3.42307) / (0.003417)

FV ≈ $128,273.36

After 29 years, the newscaster will have approximately $128,273.36 in the retirement account.

The equation of p(x) in vertex form is;

p(x) = 9.67(x + 1.04)² - 10.25

The closest answer choice is:

p(x) = 3(x - 1)²  - 2, which is not correct.

In the context of a quadratic function, the vertex is the highest or lowest point on the graph of the function. It is the point where the parabola changes direction. The vertex is also the point where the axis of symmetry intersects the parabola.

To find the vertex form of the quadratic function p(x), we need to first find the vertex, which is the point where the function reaches its maximum or minimum value.

To find the vertex, we can use the formula:

x = -b/2a, where a is the coefficient of the x²  term, b is the coefficient of the x term, and c is the constant term.

Using the table, we can see that the highest value of p(x) occurs at x = 5, and the value is 46.

We can then use the formula to find the vertex:

x = -b/2a = -5/2a

Using the values from the table, we can set up two equations:

46 = a(5)² + b(5) + c

1 = a(0)²  + b(0) + c

Simplifying the second equation, we get:

1 = c

Substituting c = 1 into the first equation and solving for a and b, we get:

46 = 25a + 5b + 1

-20 = 5a + b

Solving for b, we get:

b = -20 - 5a

Substituting b = -20 - 5a into the first equation and solving for a, we get:

46 = 25a + 5(-20 - 5a) + 1

46 = 15a - 99

145 = 15a

a = 9.67

Substituting a = 9.67 and c = 1 into b = -20 - 5a, we get:

b = -20 - 5(9.67) = -71.35

Therefore, the equation of p(x) in vertex form is:

p(x) = 9.67(x - 5)²  + 1

Simplifying, we get:

p(x) = 9.67(x²  - 10x + 25) + 1

p(x) = 9.67x²  - 96.7x + 250.85 + 1

p(x) = 9.67x²  - 96.7x + 251.85

Rounding to the nearest hundredth, we get:

p(x) = 9.67(x - 5²  + 1 = 9.67(x + 1.04)²  - 10.25

Therefore, the answer is:

p(x) = 9.67(x + 1.04)² - 10.25

The closest answer choice is:

p(x) = 3(x - 1)²  - 2, which is not correct.

To know more about vertex visit:

https://brainly.com/question/29476657

#SPJ1

the employer's total FUTA and SUTA tax is: $2,928

What is tax rate?

The percentage of income that a person or corporation must pay or withhold as taxes is known as the effective tax rate.

$7,000 (for Zachary Fox) + $7,000 (for Calvin Bell) + $7,000 (for David Alexander) + $7,000 (for Michael Sierra) = $28,000

The FUTA tax for this amount is:

$28,000 × 6.0% = $1,680

Therefore, the total taxable earnings subject to SUTA tax is:

$26,000 (for each employee) × 4 (number of employees) = $104,000

The SUTA tax for this amount is:

$104,000 × 1.2% = $1,248

The year-to-date FUTA and SUTA taxes are not given explicitly, so we cannot calculate the current period FUTA and SUTA taxes.

Therefore, the employer's total FUTA and SUTA tax is:

$1,680 (FUTA tax) + $1,248 (SUTA tax) = $2,928

To know more about tax rate visit,

https://brainly.com/question/29800484

#SPJ1

Answer:94.2

Step-by-step explanation: i think

Therefore, the height of the right triangle is 9.6 units.

A triangle is a geometric figure that consists of three line segments that intersect at three endpoints, called vertices. The line segments are called sides, and the vertices where they intersect are called angles. A triangle can be classified based on the length of its sides and the measure of its angles. Triangles are fundamental to many areas of mathematics and physics, and they have a wide range of applications in real-life situations, such as in architecture, engineering, and surveying.

Here,

To find the height of a right triangle, we can use the formula:

h = (a * b) / c

where "a" and "b" are the lengths of the legs of the right triangle, and "c" is the length of the hypotenuse.

In this case, we have a right triangle with legs of lengths 12 units and 16 units, and a hypotenuse of length 20 units. Therefore, we can substitute these values into the formula and solve for the height:

h = (12 * 16) / 20

h = 192 / 20

h = 9.6

To know more about triangle,

https://brainly.com/question/28600396

#SPJ1

The value of x from the given figure is given as follows:

144º.

An angle that measures 180 degrees is called a straight angle, and it is formed by two opposite rays that extend in opposite directions from a common endpoint, creating a straight line. A straight angle forms a straight line, and it can also be thought of as a half-turn or a semicircle.

The two opposite rays in this problem have the measures given as follows:

Hence the equation to find the value of x is given as follows:

x + x/4 = 180

x + 0.25x = 180

1.25x = 180

x = 180/1.25

x = 144º.

More can be learned about straight angles at https://brainly.com/question/24024505

#SPJ1

Thus, the time taken for the sum of $1500 to become $1600 with 6.49% simple annual interest rate is found as 1.027 years.

Simple interest is the percentage that is charged on the principal sum of money that is lent or borrowed. Similar to this, when you deposit a particular amount in a bank, you can also earn interest.

Calculating simple interest is as easy as multiplying the principal borrowed or lent, the interest rate, and the loan's term (or repayment time).

Given data:

Principal P = $1500

Amount after interest A = $1600

Rate of simple interest R = 6.49%

Time  = T years

The formula for the simple interest:

SI = PRT/100

A = P + SI

A = P + PRT/100

PRT/100 = A - P

1500*6.49*T/100 = 1600 - 1500

1500*6.49*T = 100 *100

T = 10000 / 9735

T = 1.027 years

Thus, the time taken for the sum of $1500 to become $1600 with 6.49% simple annual interest rate is found as 1.027 years.

Know more about the simple interest:

https://brainly.com/question/25793394

#SPJ1

Equations with a single unknown can be powerful tools in helping us understand complex phenomena and make predictions about how they will behave.

Yes, equations with a single unknown can be very helpful in understanding various phenomena. Mathematical equations allow us to express relationships between different variables and make predictions about how they will behave under different conditions. By solving equations, we can find the values of unknown variables and gain a deeper understanding of the system we are studying.

Other examples of equations with a single unknown that have had a significant impact include Newton's second law of motion, F=ma, which relates force (F) to mass (m) and acceleration (a), and the ideal gas law, PV=nRT, which relates pressure (P), volume (V), number of moles (n), and temperature (T) of a gas.

equations with a single unknown can be powerful tools in helping us understand complex phenomena and make predictions about how they will behave.

To know more about complex visit:

https://brainly.com/question/29377605

#SPJ1

As a result, the cylinder's volume is roughly **5541.48 mm³**.

The capacity of a cylinder is defined as its volume, and this definition aids in determining how much material the cylinder can hold .The volume of a cylinder—which corresponds to how much material can be transported inside of it or immersed in it—determines its density.. The formula r²πh, where r is the radius of the circular base and h is the height of the cylinder, determines the volume of a cylinder.

V = r²πh, where V is the volume, r is the radius of the cylinder's base, and h is the cylinder's height, is the formula for calculating a cylinder's volume.

When we enter the specified values into the formula, we obtain:

V = π(14)²(9)

V = 1764π

Rounding to the closest hundredth using 3.14, we obtain:

V ≈ 5541.48 mm³

To know more about volume of cylinder visit:

brainly.com/question/16788902

#SPJ1

Answer:

fraction form: 1/20

decimal form:0.05

63% of people Surveyed shop at a local grocery store.

A number can be expressed as a fraction of 100 using a percentage. The word "%" stands for percentage.

For instance, 50% represents 50 out of 100, or 0.5 in decimal form. Frequently, proportions, rates, and changes in quantity are represented as percentages.

In many aspects of daily life, including the calculation of sales tax, loan interest rates, and price discounts, percentages are frequently utilised. They are also employed in many academic disciplines, including math, physics, economics, and statistics.

The equality of two ratios is referred to as a percentage in mathematics. A ratio is a comparison of two amounts or values;

it is frequently stated as a fraction.

For instance, "3/5" can be used to represent the proportion of boys to girls in a classroom.

An assertion of equality between two ratios is a proportion.

For instance, the ratio of males to girls is the same as the ratio of boys to all pupils,

hence the sentence "3/5 = 6/10" is a proportion.

Analysis: -

people surveyed at store = 45

total no. of people = 72

the

Percent of peopla = 45/72  x100

= 0.625 × 100

= 62.5 %

= 63 %

63% of people Surveyed shop at a local grocery store.

To learn more about percentage visit:

https://brainly.com/question/29306119

#SPJ1

Answer:

The area of the shape is 56 to the nearest tenth

Step-by-step explanation:

r=d/2

d=2r

d=2×3=6

Area of shape=Area of rectangle+Area of semi circle

A=L×B+1/2pir²

A=7×6+1/2×22/7×3²

A=42+11/7×9

A=42+99/7

A=42+14.14

A=56.14

A=56 to the nearest tenth

If each person drove at a constant rate,than Laura drove the fastest

Displacement is the measurement of  the how far an object is out of place,therefore distance refers to  the how much ground an object has covered during its motion.so, examine the distinction between distance and displacement in this article.

The means of Speed is :he speed at which an object of location changes in any direction. The distance traveled in relation to the time it took to travel that distance is how speed is defined. The speed simply has no magnitude but it has a direction, Speed is a scalar quantity.

to compute who drove the quickest by Using this   formula

speed=Distance /time,

first of all the convert times into hours:

Hank: 3.2 hours x 3 hours and 12 minutes.

Laura: 2.5 hours is 2 hours and 30 minutes.

Nathan: 2.25 hours is 2 hours and 15 minutes.

Raquel: 4 hours plus 24 minutes equals 4.4 hours.

now to calculate the speed by above formula

Hank: 55 miles per hour for 176 miles in 3.2 hours.

Laura: 60 miles per hour equals 150 miles in 2.5 hours.

Nathan: 50 miles per houris equal to 112.5 miles in 2.25 hours.

Raquel: 65 miles for 286 miles in 4.4 hours.

As a result, Laura moved the fastest, clocking in at 60 miles. The solution, Laura, is B.

Learn more about speed here:

https://brainly.com/question/31273613

#SPJ1

Answer: 0.6954

Step-by-step explanation:

To find the area between two z scores, in this case P(-0.82<z<1.29), we can either use a z score calculator or a standard normal distribution table, which I will use for this.  

The probability of P(-0.82<z<1.29) = P(z<1.29)-(z<-0.82).

To find P(z<2.01), we use a positive z score standard normal distribution table and find that P(z<1.29)=0.9015

Using a negative z score standard normal distribution table, we can find that (z<-0.82)=0.2061.

So,  P(-0.82<z<1.29) = P(z<1.29)-(z<-0.82)=0.6954.