Answers
Answer:
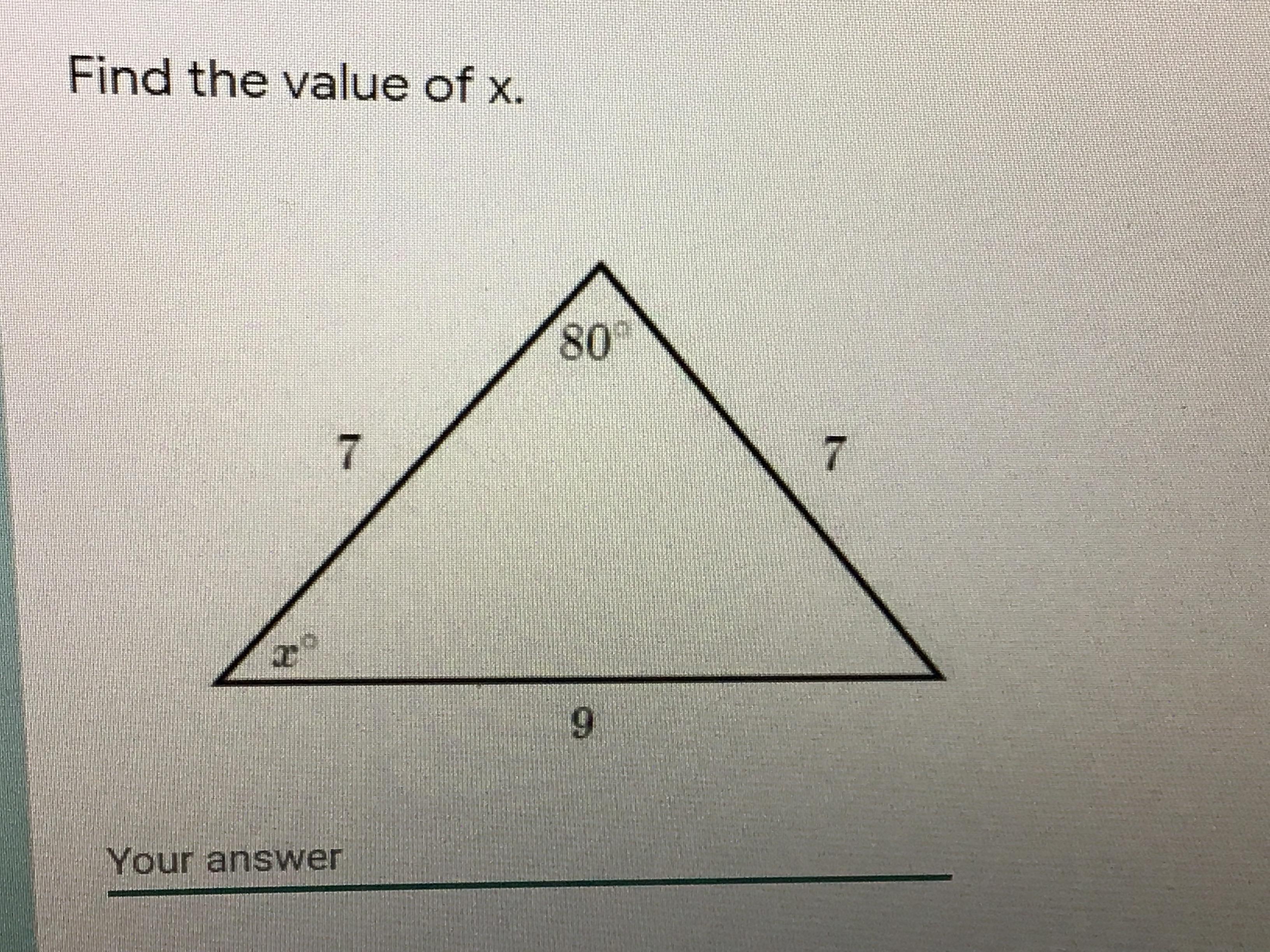
x = 50
Step-by-step explanation:
Since the triangle has 2 congruent sides then it is isosceles, thus the base angles are congruent, that is x and x
The sum of the angles in a triangle = 180°, thus
x + x + 80 = 180
2x + 80 = 180 ( subtract 80 from both sides )
2x = 100 ( divide both sides by 2 )
x = 50
Related Questions
Hey, the question is with the image. Pls help
Answers
Answer:
8
Step-by-step explanation:
Winston and Alice are taking a trip. Winston left at 8 am and traveled an average of 50 miles per hour. Alice left at 10 am and traveled an average of 70 miles per hour. At what time are they at the same place at the same time? Write a system of equation to represent this situation. Then use the substitution method with that system to determine at the time they will be in the same location. How many miles away from home will they be at that time?
Answers
Answer:
3 PM
350 miles
Step-by-step explanation:
Let's say t is the number of hours since 8 AM.
The distance traveled by Winston is:
w = 50t
The distance traveled by Alice is:
a = 70(t−2)
When w = a:
50t = 70(t−2)
50t = 70t − 140
140 = 20t
t = 7
Winston and Alice will be at the same place 7 hours after 8 AM, or 3 PM.
The distance they travel is 350 miles.
Of the cartons produced by a company, % have a puncture, % have a smashed corner, and % have both a puncture and a smashed corner. Find the probability that a randomly selected carton has a puncture or a smashed corner. The probability that a randomly selected carton has a puncture or a smashed corner nothing%. (Type an integer or a decimal. Do not round.)
Answers
Full Question
Of the cartons produced by a company, 10% have a puncture, 6% have a smashed corner, and 0.4% have both a puncture and a smashed corner. Find the probability that a randomly selected carton has a puncture or a smashed corner. The probability that a randomly selected carton has a puncture or a smashed corner nothing ____%. (Type an integer or a decimal. Do not round.)
Answer:
[tex]P(Punctured\ or\ Smashed\ Corner) = 0.156[/tex]
Step-by-step explanation:
Given
[tex]Puncture\ Corner = 10\%[/tex]
[tex]Smashed\ Corner = 6\%[/tex]
[tex]Punctured\ and\ Smashed\ Corner = 0.4\%[/tex]
Required
[tex]P(Punctured\ or\ Smashed\ Corner)[/tex]
For non-mutually exclusive event described above, P(Punctured or Smashed Corner) can be calculated as thus;
[tex]P(Punctured\ or\ Smashed\ Corner) = P(Punctured\ Corner) + P(Smashed\ Corner) - P(Punctured\ and\ Smashed\ Corner)[/tex]
Substitute:
10% for P(Puncture Corner),
6% for P(Smashed Corner) and
0.4% for P(Punctured and Smashed Corner)
[tex]P(Punctured\ or\ Smashed\ Corner) = 10\% + 6\% - 0.4\%[/tex]
[tex]P(Punctured\ or\ Smashed\ Corner) = 15.6\%[/tex]
Convert % to fraction
[tex]P(Punctured\ or\ Smashed\ Corner) = \frac{15.6}{100}[/tex]
Convert to decimal
[tex]P(Punctured\ or\ Smashed\ Corner) = 0.156[/tex]
Using Venn probabilities, it is found that:
The probability that a randomly selected carton has a puncture or a smashed corner is 15.6%.In this problem, the events are:
Event A: Puncture.Event B: Smashed corner.The "or" probability is given by:
[tex]P(A \cup B) = P(A) + P(B) - P(A \cap B)[/tex]
10% have a puncture, hence [tex]P(A) = 0.1[/tex]6% have a smashed corner, hence [tex]P(B) = 0.06[/tex].0.4% have both a puncture and a smashed corner, hence [tex]P(A \cup B) = 0.004[/tex].Then:
[tex]P(A \cup B) = 0.1 + 0.06 - 0.004 = 0.156[/tex]
The probability that a randomly selected carton has a puncture or a smashed corner is 15.6%.
To learn more about Venn probabilities, you can check https://brainly.com/question/25698611
Transformations of exponential functions
Answers
Answer:
Since the transformation is made by shifting the function right, it is a horizontal transformation.
pleassssssssssssssssssssssssseeeeeeeeeeeeeeeeeeeeeeee helpppppppppppppp meeeeeeeee i giveeeee you bralienstttttt
Answers
Answer:
487 divide by 14
Step-by-step explanation:
have a nice day
The linear combination method is applied to a system of equations as shown. 4(.25x + .5y = 3.75) → x + 2y = 15 (4x – 8y = 12) → x – 2y = 3 2x = 18
Answers
Answer:
x+2y=12-------(1)
x-2y=3---------(2)
Adding equations 1 and 2
we get
2x=18
x=9
Equation 1
9+2y=15
2y=15-9
2y=6
y=3
The solution of the given system is x=9, y=3
Step-by-step explanation
What is the answer for x? (3x-3)° [6(x-10)]
Answers
Answer:
x = 19
Step-by-step explanation:
The angles are vertical angles which means they are equal
3x-3 = 6(x-10)
Distribute
3x-3 = 6x-60
Subtract 3x from each side
3x-3 -3x = 6x-60-3x
-3 =3x-60
Add 60 to each side
-3+60 =3x-60+60
57 = 3x
Divide by 3
57/3 = 3x/3
19 =x
An accountant receives a salary of $262,000 per year. During the year, he plans to spend $99,000 on his mortgage, $54,000 on food, $32,000 on clothing, $41,000 on household expenses, and $28,000 on other expenses. With the money that is left, he expects to buy as many shares of stock at $250 per share as possible. Using the equation below, determine how many shares will he be able to buy? What was the sum of the accountant's expenses?
Answers
Answer:
Number of shares = 32 shares
Accountant total expenses= $254000
Step by step explanation:
The accountant salary is $262000
He spends $99000 on mortage
Spends $54000 on foods
Spends $32000 on clothing
Spends $41000 on household
Spends $28000 on others
Total expenses= 99000+54000+32000+41000+28000
Total expenses =$254000
Remaining money = 262000-254000
Remaining money= $8000
If shares = $250 for one
To know the amount he buys with the remaining money
We divide remaining money by shares cost
= $8000/$250
= 32 shares
What is the image of (-8, 10) when reflected in the y-axis?
Answers
Answer:
if you're just reflecting the point over the y-axis it just becomes (8,10)
Answer: (8, 10)
Explanation and Example:
I have a trick that I use. I'm not sure if it will make sense to you but I'll explain it. When the question asks you to reflect over the x-axis, then keep the x in (x,y) the same and just flip the sign for the y. If the question asks you to reflect over the y-axis, then keep y the same and flip the sign for x.
Reflect over x-axis:
(-2, 6) -----> (-2, -6)
Reflect over y-axis:
(-4, -8) -----> (4, -8)
Let A = 2, B = 3, C = 9, and D = 15.
Find the value of each expression listed below. -2 -14 10 2 -6 -10 14 6
-A + C - (D ÷ B)----------------------> (answer)
B × (-C) - (-D) + A----------------------> (answer)
(C + D) ÷ B + A----------------------> (answer)
D ÷ B + A - C----------------------> (answer)
Answers
Step-by-step explanation:
Put A = 2, B = 3, C = 9 and D = 15 to the given expressions.
Use PEMDAS.
-A + C - (D : B)
-2 + 9 - (15 : 3) = -2 + 9 - 5 = 7 - 5 = 2
B × (-C) - (-D) + A
3 × (-9) - (-15) + 2 = -27 + 15 + 2 = -12 + 2 = -10
(C + D) : B + A
(9 + 15) : 3 + 2 = 24 : 3 + 2 = 8 + 2 = 10
D : B + A - C
15 : 3 + 2 - 9 = 5 + 2 - 9 = 7 - 9 = -2
Help please! Your effort is appreciated!
Answers
Answer:
[tex]a^1[/tex]
Step-by-step explanation:
We want to rewrite [tex]\frac{a * a * a * a * a * a * a}{a * a * a* a * a * a}[/tex] in index form. That is:
[tex]\frac{a * a * a * a * a * a * a}{a * a * a * a * a * a} = \frac{a^7}{a^6}\\ \\= a^{7 - 6}\\\\= a^1[/tex]
where n = 1
6th grade math, help me please:)
Answers
Answer:
8:3 is the ratio of kids to adults
32 kids, so there are 12 adults
Answer:
32 kids to 4 adults
Step-by-step explanation:
1st row- 8 kids to 3 adults
2nd row- 16 kids to 6 adults
3rd row- 24 kids to 9 adults
4th row- 32 kids to 12 adults
consider the distribution of monthly social security (OASDI) payments. Assume a normal distribution with a standard deviation of $116. if one-fourth of payments are above $1214,87 what is the mean monthly payment?
Answers
Answer:
[tex]\mu = x - z(\sigma)[/tex]
[tex]\mu = 1214.87 - 0.67(116) \\\\\mu = 1214.87 - 77.72 \\\\\mu = \$1137.15[/tex]
Therefore, the mean monthly payment is $1137.15.
Step-by-step explanation:
What is Normal Distribution?
We are given a Normal Distribution, which is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell shaped curve represents the probability.
We are asked to find the mean monthly social security (OASDI) payment.
Mean monthly payment = μ = ?
We are given that the standard deviation is $116
One-fourth of payments are above $1214.87
One-fourth means 25%
[tex]P(X > x )= P(Z > z ) = 0.25\\\\P(X < x )= P(Z < z) = 1 - 0.25\\\\P(X < x )= P(Z < z) = 0.75\\\\[/tex]
From the z-table, the z-score corresponding to 0.75 is found to be 0.67
[tex]z = 0.67[/tex]
The mean is found by
[tex]x = \mu + z(\sigma)[/tex]
[tex]\mu = x - z(\sigma)[/tex]
Where
x = $1214.87
z = 0.67
σ = $116
[tex]\mu = 1214.87 - 0.67(116) \\\\\mu = 1214.87 - 77.72 \\\\\mu = \$1137.15[/tex]
Therefore, the mean monthly payment is $1137.15.
In a survey of 300 T.V. viewers, 40% said they watch network news programs. Find the margin of error for this survey if we want 95% confidence in our estimate of the percent of T.V. viewers who watch network news programs.
Answers
Answer:
0.05543Step-by-step explanation:
The formula for calculating the margin of error is expressed as;
[tex]M.E = z * \sqrt{\frac{p*(1-p)}{n} }[/tex] where;
z is the z-score at 95% confidence = 1.96 (This is gotten from z-table)
p is the percentage probability of those that watched network news
p = 40% = 0.4
n is the sample size = 300
Substituting this values into the formula will give;
[tex]M.E = 1.96*\sqrt{\frac{0.4(1-0.4)}{300} }\\ \\M.E = 1.96*\sqrt{\frac{0.4(0.6)}{300} }\\\\\\M.E = 1.96*\sqrt{\frac{0.24}{300} }\\\\\\M.E = 1.96*\sqrt{0.0008}\\\\\\M.E = 1.96*0.02828\\\\M.E \approx 0.05543[/tex]
Hence, the margin of error for this survey if we want 95% confidence in our estimate of the percent of T.V. viewers who watch network news programs is approximately 0.05543
Marie is saving money for home repairs. So far, she has saved $1,558. She needs at least $2,158 for the repairs. She plans to
add $60 per week to her current savings until she can afford the repairs.
In this activity, you will algebraically model and solve an inequality based on this situation and interpret the solutions within
realistic guidelines
Part A
Question
Given the situation, which inequality models the number of additional weeks Marie needs to continue saving to afford the
home repairs?
Select the correct answer.
1,558 + 60x 22,158
60x + 1,558 5 2,158
1,558 - 60x s 2,158
2,158 - 60x 2 1,558
Answers
Answer:
Inequality: [tex]1558 + 60 x \geq 2158[/tex]
Number of Weeks: [tex]x \geq 10[/tex]
Step-by-step explanation:
Given
[tex]Initial\ Savings = \$1558[/tex]
[tex]Amount\ Needed = \$2158[/tex]
[tex]Additional\ Savings = \$60\ weekly[/tex]
Required
Represent this using an inequality
Represent the number of weeks as x;
This implies that, She'll save $60 * x in x weeks
Her total savings after x weeks would be
[tex]Initial\ Savings + 60 * x[/tex]
From the question, we understand that she needs at least 2158;
Mathematically, this can be represented as (greater than or equal to 2158)
[tex]\geq 2158[/tex]
Bringing the two expressions together;
[tex]Initial\ Savings + 60 * x \geq 2158[/tex]
Substitute 1558 for Initial Savings
[tex]1558 + 60 * x \geq 2158[/tex]
[tex]1558 + 60 x \geq 2158[/tex]
Hence, the inequality that represents the situation is [tex]1558 + 60 x \geq 2158[/tex]
Solving further for x (number of weeks)
[tex]1558 + 60 x \geq 2158[/tex]
Subtract 1558 from both sides
[tex]1558- 1558 + 60 x \geq 2158 - 1558[/tex]
[tex]60x \geq 600[/tex]
Divide both sides by 60
[tex]\frac{60x}{60} \geq \frac{600}{60}[/tex]
[tex]x \geq 10[/tex]
This means that she needs to save $60 for at least 10 weeks
Answer:
Its the first one
Step-by-step explanation:
I just did it lol
Write the equation 0.3x 2 + 5x - 7 = 0 in general form and then choose the value of "b."
Answers
Answer:
3x^2 + 50x - 70 = 0
b = 50
Step-by-step explanation:
0.3x^2 + 5x - 7 = 0
Multiply both sides by 10 to get rid of the decimal coefficient.
3x^2 + 50x - 70 = 0
b = 50
what other numbers can you square that result in 9 ?
Answers
Step-by-step explanation:
I'm not sure what your answers are, but you can only square 3 and -3 to get 9.
Answer:
3, -3
Step-by-step explanation:
3*3 = 9
-3 * -3 = 9
These are the only two numbers that square to 9
Find the most general antiderivative of the function. (Check your answer by differentiation. Use C for the constant of the antiderivative.) f(x) = x2 − 7x + 5
Answers
Answer:
F(x) = [tex]\frac{x^3}{3} - \frac{7x^2}{2} + 5x + c[/tex]
Step-by-step explanation:
The antiderivative of a function (also called the integration of a function) is the reverse of the differentiation of that function. Given a function f(x), its integration, F(x), can be calculated as follows;
F(x) = [tex]\int\limits{f(x)} \, dx[/tex]
From the question, f(x) = x² - 7x + 5
Therefore,
F(x) = [tex]\int\limits {(x^2 - 7x + 5)} \, dx[/tex]
F(x) = [tex]\frac{x^3}{3} - \frac{7x^2}{2} + 5x + c[/tex]
Where c is the constant of the integration (antiderivative).
PS: The constant of integration is used for indefinite integrals and allows to express integration of a function in its most general form.
Olivia, a golfer, claims that her drive distance is more than 174 meters, on average. Several of her friends do not believe her, so she decides to do a hypothesis test, at a 10% significance level, to persuade them. She hits 15 drives. The mean distance of the sample drives is 188 meters. Olivia knows from experience that the standard deviation for her drive distance is 14 meters. H0: μ=174; Ha: μ>174 α=0.1 (significance level) What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Answers
Answer:
3.87
Step-by-step explanation:
The computation is shown below:
Data provided in the question
mean distance = [tex]\bar x[/tex] = 188 meters
Standard deviaton = [tex]\sigma = 14[/tex]
Hits drivers = 15
The distance = 174 meters
H_0: μ≤174;
H_a: μ>174
Based on the above information, the test statistic z-score is
[tex]z = \frac{\bar x - \mu }{\sigma / \sqrt{n} } \\\\ = \frac{188 - 174}{\ 14 / \sqrt{15} }[/tex]
= 3.87
Hence, the test statistic is 3.87
Note:
We take the μ≤174 instead of μ=174;
BRAINLIEST ANSWER GIVEN Without actually solving the problem, choose the correct solution by deciding which choice satisfies the given conditions. The length of a rectangle is 2 feet longer than the width. The perimeter is 20 feet. Find the dimensions of the rectangle. Length= ?; width=?
Answers
Answer:
length = 6 feetwidth = 4 feetStep-by-step explanation:
Perimeter of a rectangle = 2l + 2w
where l is the length
w is the width
The length of the rectangle is 2 feet longer than the width is written as
l = 2 + w
Perimeter = 20feet
So we have
20 = 2( 2 + w ) + 2w
20 = 4 + 2w + 2w
4w = 16
Divide both sides by 4
w = 4
Substitute w = 4 into l = 2 + w
That's
l = 2 + 4
l = 6
length = 6 feetwidth = 4 feetHope this helps you
Answer:
w = 4 and L = 10
Step-by-step explanation:
perimeter of a rectangle = 2(l+w)
p = 20
L = 2 + w
w = ?
20 = 2(2 + w + w)
20 = 2(2 + 2w)
20/2 = 2 + 2w
10 = 2 + 2w
10 - 2 = 2w
8 = 2w
w = 8/2 = 4
L = w + 2
L = 4 +2 = 6
w = 4 and L = 10
A manager receives 8 applications for a specific position. She wants to narrow it down to 5. In how many ways can she rank 5 applications?
Answers
Answer:
56 number of ways
Step-by-step explanation:
This question is a combination question since it involves selection.
Generally, if r objects are to be selected from n pool of objects, this can be done in nCr number of ways.
nCr = n!/(n-r)!r!
If a manager receives 8 applications for a specific position and wants to narrow it down to 5, the number of ways he can do this is 8C5
8C5 = 8!/(8-5)!5!
= 8!/3!5!
= 8*7*6*5!/3*2*5!
= 8*7*6/3*2
= 8*7
= 56 number of ways.
This means that the manager can rank 5 applications in 56 number of ways
The number of ways that can she rank 5 applications should be 6720.
Calculation of the number of ways:Since A manager receives 8 applications for a specific position. She wants to narrow it down to 5.
So here we do apply the permutation here:
[tex]= 8!\div 5!3! \times 5!\div 0!\\\\= 8\times 7\times 6\times 5\times 4[/tex]
= 6720
Hence, The number of ways that can she rank 5 applications should be 6720.
Learn more about ways here: https://brainly.com/question/18988173
please help me please!!!
Answers
Answer:
she has covered 6 miles in 1 ½ hours
Step-by-step explanation:
you need to learn how to read a graph.
it quite easy actually.
just look where the line on the graph is on 1.5 hours ( you can count the boxes if you don't know where 1.5 or 1 ½ is)
HeLpPPppPpppPPPPPPPppppppPPPPpppppPPPpppppPPPPPPppppppPP AGgaGAGgagagGAGin!!!!!!!!!!!!
Answers
Answer:
Pii is equAAAaaaaallLLLL to 3.14(rounded)
Step-by-step explanation:
Here listed are some formulas which can help you with your problems:
circumference of a circle=C=2πr
however, you can also write it as dπ, since is two d times r.
area of a circle= πr^2
simply plug in your values, and solve them
you have all the materials you need to know
Further assistance/spoonfeed time:
We know the formulas for the circumference and area.
We also have the values of the circles A and B.
C=2πr
That's the formula, and now I'm gonna plug in the values given to me for A, which is 21.98 for circumference, and 7 for diameter.
(21.98)=2πr
Like I said before, the radius multiplied by 2 is the diameter, which is 7. But if you actually want the radius for some reason, just divide the diameter by 2.
let's update the equation: 21.98= 7π
now divide both sides by seven, and you'll get 3.14=π
area=π^2
now do what i just did, according to this formula
Which equation shows y-5=x converted to slope intercept form.
Answers
Answer:
C) y = x + 5
Step-by-step explanation
Add 5 to both sides
The four-member math team at Pecanridge Middle School is chosen from the math club, which has three girls and five boys. How many different teams made up of two girls and two boys could be chosen?
Answers
Answer:
[tex]Total\ Selection = 30\ ways[/tex]
Step-by-step explanation:
Given
Girls = 3
Boys = 5
Required
How many ways can 2 boys and girls be chosen?
The keyword in the question is chosen;
This implies combination and will be calculated as thus;
[tex]Selection =\ ^nC_r = \frac{n!}{(n-r)!r!}[/tex]
For Boys;
n = 5 and r = 2
[tex]Selection =\ ^5C_2[/tex]
[tex]Selection = \frac{5!}{(5-2)!2!}[/tex]
[tex]Selection = \frac{5!}{3!2!}[/tex]
[tex]Selection = \frac{5 * 4 * 3!}{3!*2 * 1}[/tex]
[tex]Selection = \frac{20}{2}[/tex]
[tex]Selection = 10[/tex]
For Girls;
n = 3 and r = 2
[tex]Selection =\ ^3C_2[/tex]
[tex]Selection = \frac{3!}{(3-2)!2!}[/tex]
[tex]Selection = \frac{3!}{1!2!}[/tex]
[tex]Selection = \frac{3 * 2!}{1 *2!}[/tex]
[tex]Selection = \frac{3}{1}[/tex]
[tex]Selection = 3[/tex]
Total Selection is calculated as thus;
[tex]Total\ Selection = Boys\ Selection * Girls\ Selection[/tex]
[tex]Total\ Selection = 10 * 3[/tex]
[tex]Total\ Selection = 30\ ways[/tex]
Which group of plants were the first to adapt to life on land? flowering pine mosses conifers
Answers
Answer:
mosses
Step-by-step explanation:
use socratic
Mosses are also known as the amphibian of the plant kingdom. The mosses were the first plant that can even survive on the land.
Bryophytes:It is the group of small plants that complete its life cycle in both land and water. They were the first plants to adapt to live on the land.For example- mosses.Conifers, pines, and flowering plants developed much later after the evolution of bryophytes.
Therefore, the mosses were the first plant that can even survive on the land.
Learn more about Bryophytes:
https://brainly.com/question/841138
Which statement best describes the end behavior of the following function?
F(x) = -x3 - 2x2 +7x-10
Answers
A. The graph of the function is high on the extreme left side, and low on the extreme right side.
The graph has no "start" or "end". It's defined for all 'x' between negative and positive infinity. So no matter how far left or right you go, there's always a 'y' for whatever 'x' you're at.
But it's guaranteed that once you get far enough left (negative x), the first term -x³ will definitely be positive, and will become more and more positive as you go farther left.
And similarly, once you get far enough right (positive x), the first term, -x³ will definitely be negative, and it'll become more and more negative as you go farther right.
So, except for some wiggling within a short distance either side of the origin, if you look at this graph from 10 miles away, f(x) comes out of the sky on the left side, and it heads down into the salt mine on the right side.
Answer:
guys omg the answer is A its not a scam guys
Step-by-step explanation:
Use z scores to compare the given values. The tallest living man at one time had a height of 249 cm. The shortest living man at that time had a height of 120.2 cm. Heights of men at that time had a mean of 176.55 cm and a standard deviation of 7.23 cm. Which of these two men had the height that was more extreme?
Answers
Answer:
Step-by-step explanation:
Average height = 176.55 cm
Height of tallest man = 249 cm
Standard deviation = 7.23
z score of tallest man
= (249 - 176.55) / 7.23
= 10.02
Average height = 176.55 cm
Height of shortest man = 120.2 cm
Standard deviation = 7.23
z score of smallest man
= ( 176.55 - 120.2 ) / 7.23
= 7.79
Since Z - score of tallest man is more , his height was more extreme .
Suppose a college student pays $750 for tuition fees. However, she also has to pay $300 for her textbooks (ouch!). What percent of her total education costs does she pay for her books?
Answers
Answer:
Total costs = $700 + $300 = $1000.
$300 / $1000 = 0.3 = 3%
Step-by-step explanation:
Find the sum of 1342, -295, -456,89.
Answers
Answer:
680
Step-by-step explanation:
add 1342+89 to get 1431
then add -295+-456 to get -751
then subtract 751 from 1431 to get 680
Step-by-step explanation:
Hope this is correct and helpful
HAVE A GOOD DAY!