Answers
Answer:
To find out how many more feet Peyton needs to walk to reach her goal of 10,000 steps, we can multiply the remaining number of steps by the average distance per step.
Total steps Peyton needs to reach her goal = 10,000 - 7,338 = 2,662 steps
Average distance per step = 2.5 feet
Total distance Peyton needs to cover = Total steps × Average distance per step
= 2,662 × 2.5
= 6,655 feet
Therefore, Peyton needs to walk 6,655 more feet to reach her goal of 10,000 steps.
Answer:
peyton needs to walk a total of 6655feets more
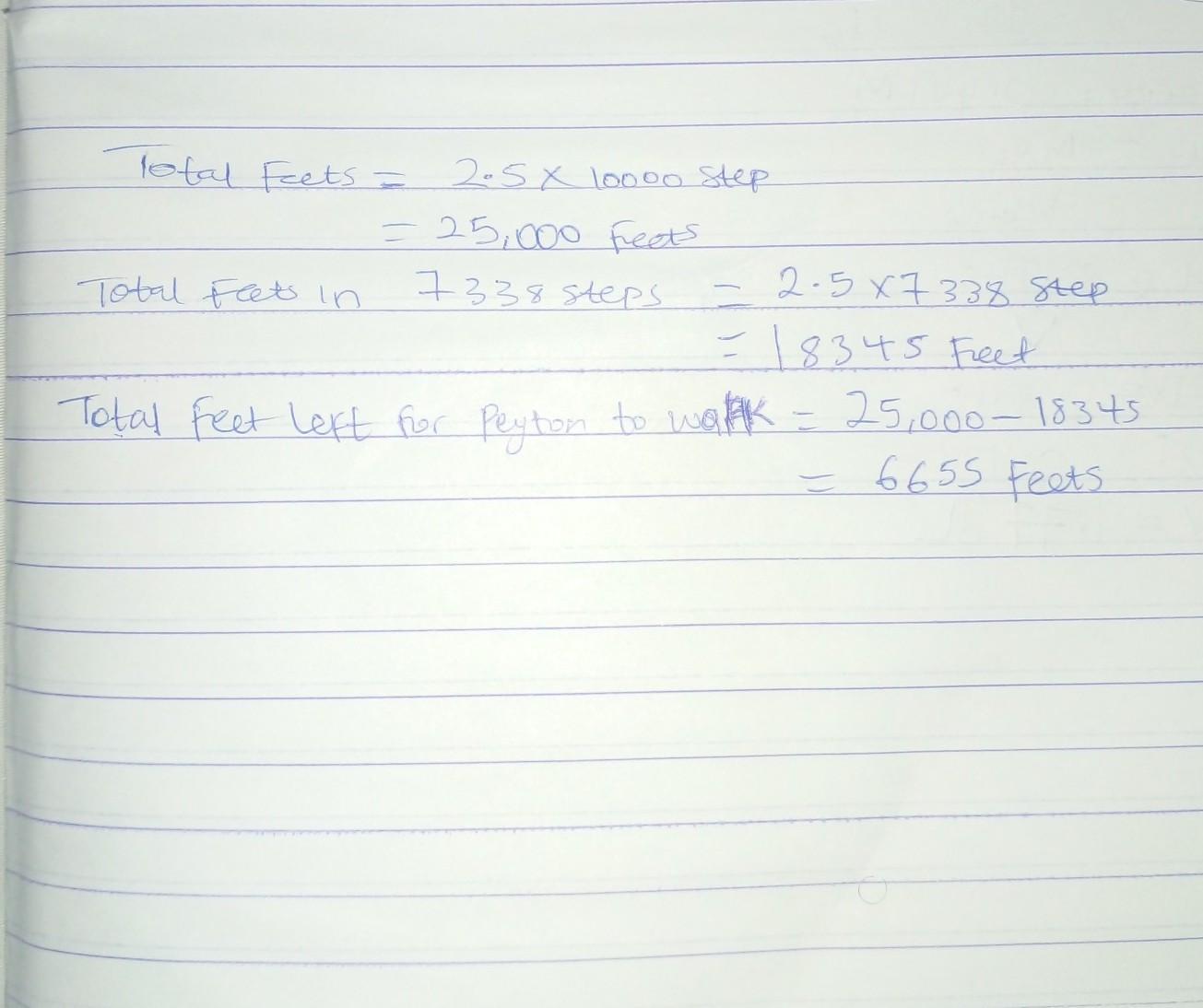
Related Questions
1. You go to the ice cream shop with your friends and you can choose an ice cream, a topping
and sprinkles. How many different sundaes can you make when you order one flavor of ice
cream, one topping and one color of sprinkles from the chart below? Show all possible
outcomes in a tree diagram.
Ice Cream
Chocolate
Vanilla
Strawberry
Topping
Fudge
Marshmallow
Sprinkles
Chocolate
Rainbow
a. How many sample spaces are there? HINT: How many possible combinations?
b. P (Chocolate, Fudge, Rainbow)
Answers
A. There are 9 sample spaces.
B. The probability of choosing Chocolate, Fudge, and Rainbow is 1/9
What is meant by sample spaces?
In probability theory, a sample space is the set of all possible outcomes of a random experiment or process. It is used to define the space of events and calculate probabilities.
What is meant by probability?
Probability is a measure of the likelihood of an event occurring, expressed as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. It is calculated by dividing the number of favourable outcomes by the total number of possible outcomes.
According to the given information
A. There are 9 possible combinations (3 ice cream flavors x 3 toppings x 1 sprinkle color), so there are 9 sample spaces.
B. The probability of choosing Chocolate, Fudge, and Rainbow is 1/9, assuming all combinations are equally likely.
To know more about probability visit
brainly.com/question/30034780
#SPJ1
Lastly, let’s consider the alternative method of paying for college: paying with loans. You take out a loan in the amount of your tuition and fees cost for 5 years rounded up to the nearest thousand dollars (for example if the total cost is $55,787 the loan would be for $56,000). The loan has a monthly interest rate of 0.25% and a monthly payment of $250. How long will it take you to pay off the loan? Use the formula N= (-log(1-i*A/P))/(log(1+i)) to determine the number of months it will take you to pay off the loan. Let N represent the number of monthly payments that will need to be made, i represent the interest rate in decimal form, A represent the amount owed (total amount of the loan), and P represent the amount of your monthly payment. Be sure to show your work for all calculations made.
Answers
With given compound interest, it will take 27.25 years to pay off the loan.
What is Compound interest?
Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, the interest that is earned on both the principal amount and any previously accumulated interest. In other words, it is interest that is calculated not only on the original amount of money but also on any interest that has been earned previously. This can result in significant growth of an investment or loan balance over time, as the interest earned on the accumulated interest can compound exponentially. Compound interest can be calculated using a specific formula that takes into account the principal amount, the interest rate, and the compounding frequency.
Now,
First, we need to calculate the total amount of the loan. We round up the tuition and fees cost for 5 years to the nearest thousand dollars:
Total cost = $70,000
Rounded up to nearest thousand = $70,000
So, the amount of the loan is $70,000.
Next, we can use the formula N= (-log(1-i*A/P))/(log(1+i)) to calculate the number of monthly payments needed to pay off the loan.
N = (-log(1-0.0025*70000/250))/(log(1+0.0025))
N = (-log(1.75))/(log(1.0025))
N = 326.45
Rounding up to the nearest whole number, it will take 327 monthly payments to pay off the loan.
So, it will take 327/12 = 27.25 years to pay off the loan.
To know more about Compound Interest visit the link
brainly.com/question/14295570
#SPJ1
Which geometric term describes ∠ T A G ?
Answers
Answer:
angle
Step-by-step explanation:
since there is a < sign, that makes it an angle. I'm not sure if that is the whole problem, or if It is missing a picture. Hope this helps!
Answer: i know it is acute
Complete the truth table for (A ⋁ B) ⋀ ~(A ⋀ B).
Answers
The truth table for (A ⋁ B) ⋀ ~(A ⋀ B) is:
A B (A ⋁ B) ⋀ ~(A ⋀ B)
0 0 0
0 1 0
1 0 0
1 1 0
The truth table is what?A truth table is a table that displays all possible combinations of truth values (true or false) for one or more propositions or logical expressions, as well as the truth value of the resulting compound proposition or expression that is created by combining them using logical operators like AND, OR, NOT, IMPLIES, etc.
The columns of a truth table reflect the propositions or expressions themselves as well as the compound expressions created by applying logical operators to them. The rows of a truth table correspond to the various possible combinations of truth values for the propositions or expressions.
To complete the truth table for (A ⋁ B) ⋀ ~(A ⋀ B), we need to consider all possible combinations of truth values for A and B.
A B A ⋁ B A ⋀ B ~(A ⋀ B) (A ⋁ B) ⋀ ~(A ⋀ B)
0 0 0 0 1 0
0 1 1 0 1 0
1 0 1 0 1 0
1 1 1 1 0 0
So, the only case where the expression is true is when both A and B are true, and for all other cases it is false.
To know more about truth tables, visit:
https://brainly.com/question/31482105
#SPJ1
A stainless-steel patio heater is shaped like a square pyramid. The length of one side of the base is 10 feet. The slant height is 12 feet. What is the height of the heater? Round to the nearest tenth of a foot.
Answers
The height of the heater is approximately 6.6 feet.
What is Pythagoras theorem?According to Pythagoras's Theorem, the square of the hypotenuse side in a right-angled triangle is equal to the sum of the squares of the other two sides. Perpendicular, Base, and Hypotenuse are the names of this triangle's three sides.
We can use the Pythagorean theorem to find the height of the pyramid. Let's call the height "h". Then, the slant height is the hypotenuse of a right triangle with base and height both equal to 10 feet, so we have:
h² + 10² = 12²
Simplifying and solving for h, we get:
h² + 100 = 144
h² = 44
h ≈ 6.6 feet
Therefore, the height of the heater is approximately 6.6 feet.
Learn more about Pythagoras theorem on:
https://brainly.com/question/231802
#SPJ1
Help me pleas whith this
Answers
13. What is the surface area of a dome (a half sphere) with a radius of 12 meters?
288 meters squared
48 meters squared
967 meters squared
576 meters squared
Answers
Answer: The formula for the surface area of a sphere is given by 4πr^2, and since we have half of a sphere, the surface area of a dome (a half sphere) is 2πr^2.
Plugging in the radius r = 12 meters, we get:
Surface area = 2π(12)^2
Surface area = 2π(144)
Surface area ≈ 904.78
Rounding to the nearest whole number, we get the surface area of the dome as 905 meters squared. Therefore, the closest answer choice is 967 meters squared.
So the answer is: 967 meters squared.
Step-by-step explanation:
Suppose that the function h is defined as follows.
if
-2
-1
h(x)= 0
1
2
Graph the function h.
-3.5
if-2.5
if-1.5
if -0.5
if 0.5 ≤x≤1.5
+
X
Ś
Answers
The required graph of the function given; h (x) has been attached.
Define a graph?In mathematics, graph theory is the study of graphs, which are mathematical structures used to represent pairwise interactions between objects. In this definition, a network is made up of nodes or points called vertices that are connected by edges, also called links or lines. In contrast to directed graphs, which have edges that connect two vertices asymmetrically, undirected graphs have edges that connect two vertices symmetrically. Graphs are one of the primary areas of study in discrete mathematics.
Here as per the question the graph of the function, h (x) has been attached.
To know more about graphs, visit:
brainly.com/question/17267403
#SPJ1
please help me
To begin a bacteria study, a petri dish had 2300 bacteria cells. Each hour since, the number of cells has increased by 12%.
Let t be the number of hours since the start of the study. Let y be the number of bacteria cells.
Write an exponential function showing the relationship between y and t.
Answers
The exponential function showing the relationship is y = 2300(1 + 0.12)^t
The exponential function showing the relationshipThe exponential function showing the relationship between y and t can be written as:
y = 2300(1 + 0.12)^t
where 2300 is the initial number of bacteria cells, 0.12 is the growth rate (12% expressed as a decimal), and t is the time in hours since the start of the study.
This function is obtained by using the formula for exponential growth, which is y = a(1 + r)^t, where a is the initial amount, r is the growth rate, and t is the time.
In this case, a = 2300, r = 0.12, and y represents the amount of bacteria cells after t hours.
Read more about exponential function at
https://brainly.com/question/2456547
#SPJ1
solve for the unknown to find the unit rate
1/5 ?
----- = -----
1/20 1
Answers
Answer: 4
Step-by-step explanation:
To find the unit rate, we can cross-multiply the fractions.
Multiplying the numerator of the first fraction by the denominator of the second fraction, we get 1/5.
Multiplying the numerator of the second fraction by the denominator of the first fraction, we get 1/20.
Now we have the equation 1/5 = 1/20.
To solve for the unknown, we can cross-multiply again, which gives us 20 * 1/5 = 4.
Therefore, the unit rate is 4.
solve the equation
a) y''-2y'-3y= e^4x
b) y''+y'-2y=3x*e^x
c) y"-9y'+20y=(x^2)*(e^4x)
Answers
Answer:
a) To solve the differential equation y''-2y'-3y= e^4x, we first find the characteristic equation:
r^2 - 2r - 3 = 0
Factoring, we get:
(r - 3)(r + 1) = 0
So the roots are r = 3 and r = -1.
The general solution to the homogeneous equation y'' - 2y' - 3y = 0 is:
y_h = c1e^3x + c2e^(-x)
To find the particular solution, we use the method of undetermined coefficients. Since e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = Ae^4x
Taking the first and second derivatives of y_p, we get:
y_p' = 4Ae^4x
y_p'' = 16Ae^4x
Substituting these into the original differential equation, we get:
16Ae^4x - 8Ae^4x - 3Ae^4x = e^4x
Simplifying, we get:
5Ae^4x = e^4x
So:
A = 1/5
Therefore, the particular solution is:
y_p = (1/5)*e^4x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^3x + c2e^(-x) + (1/5)*e^4x
b) To solve the differential equation y'' + y' - 2y = 3xe^x, we first find the characteristic equation:
r^2 + r - 2 = 0
Factoring, we get:
(r + 2)(r - 1) = 0
So the roots are r = -2 and r = 1.
The general solution to the homogeneous equation y'' + y' - 2y = 0 is:
y_h = c1e^(-2x) + c2e^x
To find the particular solution, we use the method of undetermined coefficients. Since 3xe^x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax + B)e^x
Taking the first and second derivatives of y_p, we get:
y_p' = Ae^x + (Ax + B)e^x
y_p'' = 2Ae^x + (Ax + B)e^x
Substituting these into the original differential equation, we get:
2Ae^x + (Ax + B)e^x + Ae^x + (Ax + B)e^x - 2(Ax + B)e^x = 3xe^x
Simplifying, we get:
3Ae^x = 3xe^x
So:
A = 1
Therefore, the particular solution is:
y_p = (x + B)e^x
Taking the derivative of y_p, we get:
y_p' = (x + 2 + B)e^x
Substituting back into the original differential equation, we get:
(x + 2 + B)e^x + (x + B)e^x - 2(x + B)e^x = 3xe^x
Simplifying, we get:
-xe^x - Be^x = 0
So:
B = -x
Therefore, the particular solution is:
y_p = xe^x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^(-2x) + c2e^x + xe^x
c) To solve the differential equation y" - 9y' + 20y = x^2*e^4x, we first find the characteristic equation:
r^2 - 9r + 20 = 0
Factoring, we get:
(r - 5)(r - 4) = 0
So the roots are r = 5 and r = 4.
The general solution to the homogeneous equation y" - 9y' + 20y = 0 is:
y_h = c1e^4x + c2e^5x
To find the particular solution, we use the method of undetermined coefficients. Since x^2*e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax^2 + Bx + C)e^4x
Taking the first and second derivatives of y_p, we get:
y_p' = (2Ax + B)e^4x + 4Axe^4x
y_p'' = 2Ae^4x +
The circle graph below shows the number of animals in Mushu's farm. Sheep Donkeys Camels Goats Cows If there were 24 goats, how many cows are there in the farm?
Answers
By assuming that the farmer has goat and cows in the ratio 3:4, the number of cows in the farm will be 32 cows.
If there were 24 goats, how many cows are there in the farm?To find out how many cows are in the farm, we need to know the total number of animals in the farm. Assuming the ratio of goats to cows is 3:4, we can write this as: [tex]3x : 4x[/tex]
Where 3x represents the number of goats, and 4x represents the number of cows. If we know that there are 24 goats, we can set up an equation to solve for x:
3x = 24
Dividing both sides by 3, we get:
x = 8
Now that we know the value of x, we can find the number of cows:
= 4x
= 4(8)
= 32
Therefore, there are 32 cows in the farm.
Read more about ratio
brainly.com/question/12024093
#SPJ1
PLEASE HELP
Find the Area
2cm
___cm^2
Answers
Answer:
3.14 cm^2
Step-by-step explanation:
1. Find radius:
If diameter is 2, divide it by 2 to get radius = 1
2. Find formula:
A=πr^2
3. Plug in:
A = π(1)^2
4. Solve (multiply):
A = π(1)^2:
3.14159265359
Or
3.14 cm^2
Answer:
3.14 cm^2
Step-by-step explanation:
A=[tex]\pi[/tex]r^2
r=2
2/2=1
A=[tex]\pi[/tex](1)^2
=[tex]\pi[/tex]1
≈3.14x1
≈3.14cm^2
The monthly cost (in dollars) of a long-distance phone plan is a linear function of the total calling time (in minutes). The monthly cost for 35 minutes of calls is $16.83 and the monthly cost for 52 minutes is $18.87. What is the monthly cost for 39 minutes of calls?
Answers
Answer: We can use the two given points to find the equation of the line and then plug in 39 for the calling time to find the corresponding monthly cost.
Let x be the calling time (in minutes) and y be the monthly cost (in dollars). Then we have the following two points:
(x1, y1) = (35, 16.83)
(x2, y2) = (52, 18.87)
The slope of the line passing through these two points is:
m = (y2 - y1) / (x2 - x1) = (18.87 - 16.83) / (52 - 35) = 0.27
Using point-slope form with the first point, we get:
y - y1 = m(x - x1)
y - 16.83 = 0.27(x - 35)
Simplifying, we get:
y = 0.27x + 7.74
Therefore, the monthly cost for 39 minutes of calls is:
y = 0.27(39) + 7.74 = $18.21
Step-by-step explanation:
Write an equation in point-slope form. Part I: Create an equation of a line in point-slope form. Be sure to identify all parts of the equation before writing the equation. (3 points) Part II: Using the equation of the line you wrote in Part I, write an equation of a line that is perpendicular to this line. Show your work. (3 points)
Answers
The line's equation in point-slope form is shown here. Point (2, 5) is the given point on the line, and slope 2 is the given slope of the line. The slope of this line is -1/2, which is the negative reciprocal of the slope.
How do you formulate an equation in point-slope form?A line's point slope form equation is [tex]y - y_1 = m(x - x_1)[/tex]. Consequently, y - 0 = m(x = 0), or y = mx, is the equation of a line passing through the origin with a slope of m.
We require a point on the line and the slope of the line in order to create a line equation in point-slope form. In point-slope form,
[tex]y - y1 = m(x - x1)[/tex]
As an illustration, suppose we want to formulate the equation of the line passing through the coordinates (2, 5) and having a slope of 2. The values can be entered into the point-slope form as follows:
y - 5 = 2(x - 2)Let's say the given line has the equation [tex]y - y1 = m(x - x1)[/tex], where (x1, y1) is a point on the line and m is the slope of the line.
we can use the given point (2, 5). Then we can plug in the values into the point-slope form:
[tex]y - 5 = (-1/2)(x - 2).[/tex]
To know more about point-slope visit:-
brainly.com/question/837699
#SPJ1
You can afford a $1000 per month mortgage payment. You've found a 30 year loan at 5.3% interest.
a) How big of a loan can you afford? (Round to the nearest cent, as needed.)
$
b) How much total money will you pay the loan company? (Round to the nearest cent, as needed.)
$
c) How much of that money is interest? (Round to the nearest cent, as needed.)
Answers
Answer:
a) To find out how big of a loan you can afford, we can use the formula for the monthly payment of a mortgage:
M = P [ i(1 + i)^n ] / [ (1 + i)^n - 1 ]
where M is the monthly payment, P is the principal (the amount borrowed), i is the monthly interest rate (which is the annual interest rate divided by 12), and n is the number of monthly payments (which is the number of years times 12).
In this case, we know that M = $1,000, i = 0.053/12, and n = 30 x 12 = 360. We want to solve for P, the principal we can afford.
Substituting these values into the formula, we get:
$1,000 = P [ 0.004416(1 + 0.004416)^360 ] / [ (1 + 0.004416)^360 - 1 ]
Simplifying and solving for P, we get:
P = $183,928.72
Therefore, you can afford a loan of approximately $183,928.72.
b) The total money paid to the loan company will be the monthly payment multiplied by the number of payments over the life of the loan. In this case, we have:
Total money paid = $1,000 x 360 = $360,000
Therefore, the total amount of money paid to the loan company will be $360,000.
c) To find out how much of that money is interest, we can subtract the principal from the total amount paid. In this case, we have:
Interest paid = Total money paid - Principal = $360,000 - $183,928.72 = $176,071.28
Therefore, the amount of money paid in interest will be $176,071.28.
Please help me solve and show my work
Answers
The degree measure of the angles are;
1. 5π/3 = 300°
2 3π/4 = 135°
3. 5π/6 = 150°
4. -3π/2 = 90°
What is degree and radian?A degree is a unit of measurement which is used to measure circles, spheres, and angles while a radian is also a unit of measurement which is used to measure angles.
A circle has 360 degrees which are its full area while its radian is only half of it which is 180 degrees or one pi radian.
therefore π = 180°
1. 5π/ 3 = 5×180/3 = 300°
2. 3π/4 = 3× 180/4 = 540/4 = 135°
3. 5π/6 = 5×180/6 = 150°
4. - 3π/2 = -3 × 180/2 = -270° = 90°
learn more about degree and radian from
https://brainly.com/question/22689613
#SPJ1
2. Mrs. Cooper created a triangular shaped vegetable garden and needs to put down fertilizer to cover the space. If the garden has a base of 8m and a height of 10m, how much fertilizer will she need?
Answers
Answer:
40 m²
Step-by-step explanation:
Area of triangle:
To find the area of triangle, multiply the base and area and then divide it by 2.
base = b = 8 m
height = h = 10m
[tex]\boxed{\bf Area \ of \ triangle = \dfrac{1}{2}*b*h}[/tex]
[tex]= \dfrac{1}{2}*8 * 10\\\\= 4 * 10\\\\= 40 \ m^2[/tex]
please answer in detail
Answers
Answer:
AB: y = 2x + 4
Step-by-step explanation:
Line AB is parallel to the line y = 2x + 3
When 2 lines are parallel they have the same coefficient of x.
=> AB: y = 2x + m (1)
Because line AB passes through the point (0, 4)
Replace x = 0; y = 4 into (1) => 2 × 0 + m = 4 => m = 4
So AB: y = 2x + 4
Which equations can be used to solve for y, the length of the room? Select three options. y(y + 5) = 750 y2 – 5y = 750 750 – y(y – 5) = 0 y(y – 5) + 750 = 0 (y + 25)(y – 30) = 0
Answers
The equations that can be used to solve for y are y(y + 5) = 750, y² – 5y = 750 and y(y – 5) + 750 = 0
What is quadratic equation?
it's a second-degree quadratic equation which is an algebraic equation in x. Ax2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term, is the quadratic equation in its standard form.
The equations that can be used to solve for y, the length of the room are:
1. y(y + 5) = 750
2. y² – 5y = 750
3. y(y – 5) + 750 = 0
Option 1 and 2 are quadratic equations that can be solved by factoring, completing the square, or using the quadratic formula. Option 3 is also a quadratic equation but it requires rearranging to the standard form before applying the same methods. The last option, (y + 25)(y – 30) = 0, is not a quadratic equation but it can be easily solved using the zero product property.
To learn more about quadratic equation from the given link:
brainly.com/question/30098550
#SPJ1
how am i supposed to prove that theyre collinear
Answers
Answer:
They are collinear if they are on the same line
if f(x)= -3, then f'(x)=?
Answers
Answer:
0
Step-by-step explanation:
0
What is the mean of the values in the stem-and-leaf plot?
Enter your answer in the box.
Answers
Answer:
mean = 24
Step-by-step explanation:
the mean is calculated as
mean = [tex]\frac{sum}{count}[/tex]
the sum of the data set is
sum = 12 + 13 + 15 + 28 + 28 + 30 + 42 = 168
there is a count of 7 in the data set , then
mean = [tex]\frac{168}{7}[/tex] = 24
Triangle PQR is drawn with coordinates P(0, 2), Q(0, 5), R(1, 4). Determine the translation direction and number of units if R′(−7, 4).
8 units down
8 units up
8 units to the right
8 units to the left
Answers
It follows that the translation direction is 8 units to the left and 0 units up or down.
Describe translation?A translation is a geometric change in Euclidean geometry where each point in a figure, shape, or space is moved uniformly in one direction. A translation can either be thought of as moving the origin of the coordinate system or as adding a constant vector to each point
The new vertices of a triangle with vertex locations of (0,0), (1,0), and (0,1), for instance, would be (2,3, (3,3), and (2,4) if the triangle were translated 2 units to the right and 3 units up.
We can use the following procedures to get the translation direction and number of units for R′(7, 4):
1. Determine the difference between R and R′'s x-coordinates: −7 − 1 = 8
2. Determine the difference between R and R′'s y coordinates: 4 − 4 = 0
It follows that the translation direction is 8 units to the left and 0 units up or down.
To know more about translation visit:
brainly.com/question/12463306
#SPJ1
See the photo below
Answers
This problem involves integration and algebraic manipulation, and belongs to the subject of calculus. The solutions are:
[tex]A) $\int_{0}^{2} (f(x) + g(x)) dx = -3$[/tex]
[tex]B) $\int_{0}^{3} (f(x) - g(x)) dx = -4$[/tex]
[tex]C) $\int_{2}^{3} (3f(x) + g(x)) dx = -32$[/tex]
What is the explanation for the above response?
This is a problem that asks us to find the values of some definite integrals using given values of other definite integrals. We are given three definite integrals, and we are asked to compute three other integrals involving the same functions, using the given values.
The problem involves some algebraic manipulation and the use of the linearity of the integral.
It also involves finding the constant "a" that makes a definite integral equal to zero. The integral involves two functions, "f(x)" and "g(x)," whose definite integrals over certain intervals are also given.
See the attached for the full solution.
Learn more about integration at:
https://brainly.com/question/18125359
#SPJ1
Find the surface area. Round to the nearest hundredth
Answers
Answer:
122.30 cm²
Step-by-step explanation:
Divide the polyhedron into shapes:
+) 2 triangles with the same area.
The area of the triangle is
(4.3×11)÷2 = 23.65 cm².
And with two triangles of the same area we take the sum of both areas
23.65 + 23.65 = 47.3 cm²
+) 3 rectangles with different areas.
(3×6) + (3×8) + (3×11) = 75 cm²
So the surface area is the sum of areas of the triangles and rectangles
47.3 + 75 = 122.3 = 122.30 cm²
If you have a standard score of Z = 1, what percentage of the population has scores less than you?
Answers
Step-by-step explanation:
From a z-score table
z-score = 1 corresponds to .8413 or 84.13 percentile
meaning 84 .13 % have a lesser score than you
Use the graph to answer the questions for the questions
Answers
The vertex is (50, 630). The vertex is the peak and correspond with the coordinates of he maximum height of the arch.
The solutions is the base of the arch and this (20, 0) and (80, 0)
vertex form, y = -0.7(x - 50)² + 630
Quadratic equation factored form, y = -0.7 (x - 80) (x - 20)
The equations are the same when plotted on a graph and examined mathematically. physically it looks different.
the domain is (-∞, ∞)
The height of the monument 15 feet from the left side is 472.5 feet
How to find the quadratic equationsince the zeroes of the quadratic equation is (20, 0) and (80, 0), hence we have that
y = a(x - 20)(x - 80) and the equation pass points (50, 630)
630 = a(50 - 20)(50 - 80)
630 = a * 30 * -30
630 = -900a
a = -0.7
Quadratic equation has a standard vertex form, y = a(x - h)² + k
y = a(x - h)² + k
vertex (h, k) = (50, 630) and a = -0.7
plugging the values
y = -0.7(x - 50)² + 630
Quadratic equation has a standard factored form, y = a(x - h)² + k
y = a(x - r2)(x - r1)
where r2 and r1 are the roots r1 = 20 r2 = 80 an a = -0.7
plugging the values
y = -0.7 (x - 80)(x - 20)
The height of the monument 15 feet from the left side is gotten from the graph
this is 15 feet from 20 hence x = 35 feet
from the graph it can traced to be 472.5 feet
Learn more about quadratic equation at
https://brainly.com/question/24334139
#SPJ1
The diameter of a circle is 38 feet.what is the circles circumfrence. Use 3.14 for pi
Answers
Answer:
The circumference of the circle is 119.32 ft.
Step-by-step explanation:
The circumference of a circle can be solved through the formula:
C = πd
where d is the diameter
Given: d = 38 ft
π = 3.14
Solve:
C = πd
C = 3.14 (38 ft)
C = 119.32 ft
Given the expression 3x+2 evaluate the expression for the given values of x when x=(-2)
Answers
Answer:
...............................
The answer is -4.
Explanation:
First, plug the value of x in.
3(-2)+2
Then, multiply 3 and -2 since they are next to each other and order of operations PEMDAS tells you to multiply first.
-6+2
Lastly, add -6 and 2 to get -4.
