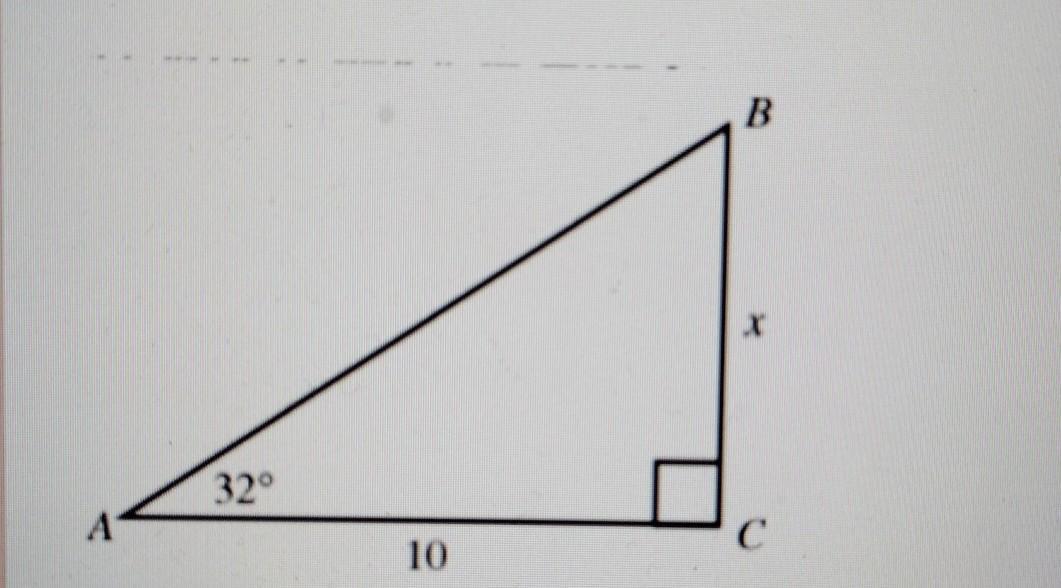
In the accompanying diagram, m<A=32° and AC = 10. Which equation could be used to find x in ∆ABC?
1. x=10 sin [32°]
2. x=10 cos [32°]
3. x = 10 tan [32°]
4. x=10/cos32
Answers
The equation x = 10 tan (32°) could be used to find x in ∆ABC.
RIGHT TRIANGLEA triangle is classified as a right triangle when it presents one of your angles equal to 90º. The greatest side of a right triangle is called the hypotenuse. And, the other two sides are called legs.
The math tools applied for finding angles or sides in a right triangle are the trigonometric ratios or the Pythagorean Theorem.
The Pythagorean Theorem says: (hypotenuse)²= (leg1)²+(leg2)² . And the main trigonometric ratios are: sin (x) , cos (x) and tan (x) , where:
[tex]sin(x)=\frac{opposite\ side}{hypotenuse} \\ \\ cos(x)=\frac{adjacent\ side}{hypotenuse}\\ \\ tan(x)=\frac{sin(x)}{cos(x)} =\frac{opposite\ side}{adjacent\ side}[/tex]
The question gives the value of the two sides and the value of an angle. From the trigonometric ratios presented before, you can write:
[tex]tan(32)=\frac{opposite\ side}{adjacent\ side}=\frac{x}{10} \\ \\ x=10\ tan (32\°)[/tex]
Read more about trigonometric ratios here:
brainly.com/question/11967894
#SPJ1
Related Questions
in an integer overflow attack, an attacker changes the value of a variable to something outside the range that the programmer had intended by using an integer overflow.T/F
Answers
True. An integer overflow attack occurs when an attacker manipulates a variable in a way that causes it to exceed its maximum value or minimum value, leading to unexpected and potentially harmful behavior.
This can happen if a programmer fails to properly check and validate the input values that are being used in their code, allowing an attacker to inject a value that triggers an overflow.
As a result, the variable may be assigned a value that is outside the intended range, leading to unpredictable behavior and potentially causing the program to crash or execute unintended code. It is important for programmers to take steps to prevent integer overflow attacks, such as validating input values and using data types with sufficient capacity to hold the expected range of values.
This occurs when an arithmetic operation results in a value that is too large to be stored in the allocated memory, causing the value to wrap around and become smaller, or even negative. This can lead to unintended consequences in a program's behavior, which an attacker can exploit to gain unauthorized access or cause other security issues.
To learn more about integer overflow attack: brainly.com/question/30906850
#SPJ11
If r=0.5 m, A = ???
(Use the r key.)
Answers
The calculated value of the angular velocity of the object is 2 rad/s.
Calculating the angular velocityThe angular velocity, denoted by the Greek letter omega (ω), represents the rate of change of the angle with respect to time.
For an object moving in a circular path, the angular velocity is related to the linear speed and the radius of the circle by the equation:
ω = v/r
where v is the linear speed and r is the radius.
In this case, the radius is 0.5m and the speed is 1ms−1. Thus, the angular velocity is:
ω = v/r = 1/0.5 = 2 radians per second (rad/s)
Therefore, the angular velocity of the object is 2 rad/s.
Read more about angular velocity at
https://brainly.com/question/9408577
#SPJ1
Complete question
An object moves in a circular path of radius 0.5m with a speed of 1ms−1. What is its angular velocity (A)?
If r = 0.5 m, A = ???
What is the length of XW and what is the length of WV?
Answers
The value of length XW and WV are 20 and 25 respectively.
What are similar triangles?Similar triangles are triangles that have the same shape, but their sizes may vary. The ratio of corresponding sides of similar triangles are equal.
Therefore XW/VW = XY/XZ
= XW/45 = 24/54
54(XW) = 45× 24
54(XW) = 1080
divide both sides by 54
XW = 1080/54
XW = 20
Therefore WV can be found by subtracting XW for VX
= 45-20 = 25
therefore the value of XW and WV are 20 and 25 respectively.
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
armer abe has a budget of $300 to build a rectangular pen to protect his rambunctious sheep. he decides that three sides of the pen will be constructed with chain-link fence, which costs only $1 per foot. farmer abe decides that the fourth side of the pen will be made with sturdier fence, which costs $5 per foot. find the dimensions of the largest area the pen can enclose.
Answers
Let x be the length of the pen and y be the width of the pen.
The total cost of the pen is given by:
Cost = 3x + 5y = 300
3x + 5y = 300
3x = 300 - 5y
x = (300 - 5y)/3
The area of the pen is given by:
Area = xy = (300 - 5y)/3 * y
in a recent basketball game, shenille attempted only three-point shots and two-point shots. she was successful on 20% of her three-point shots and 30% of her two-point shots. shenille attempted 30 shots. how many points did she score?(2013 amc 12a
Answers
The probability of a score for a recent basketball game, shenille attempted only three-point shots and two-point shots is 18 points in the game. The answer is Option B.
Let x be the number of three-point shots and y be the number of two-point shots attempted by Shenille.
Then, we have:
x + y = 30 (total number of shots attempted)
Let's solve for one of the variables. For example, we can solve for x by subtracting y from both sides of the equation:
x = 30 - y
Now, we can express Shenille's points in terms of x and y:
Points = 3x + 2y
Substituting x = 30 - y, we get:
Points = 3(30 - y) + 2y
Points = 90 - y
Shenille's success rate for three-point shots is 20%, so the number of successful three-point shots she made is 0.2x. Similarly, the number of successful two-point shots she made is 0.3y.
Total points scored = (0.2x)(3) + (0.3y)(2)
Substituting x = 30 - y, we get:
Total points scored = (0.2(30 - y))(3) + (0.3y)(2
Total points scored = 18 + 0.4y
Now we need to maximize the total points scored by Shenille. Since she attempted 30 shots in total, we have:
y = 30 - x
Substituting this into the equation for total points, we get:
Total points scored = 18 + 0.4(30 - x)
Total points scored = 30 - 0.4x
This is a linear function, which is maximized at its endpoint. The maximum value of this function occurs at x = 0, which means Shenille attempted all two-point shots. In this case, y = 30, and the total points scored would be:
Total points scored = 0 + 0.3(30)(2)
Total points scored = 18
Learn more about probability at
https://brainly.com/question/30034780
#SPJ4
The question is -
In a recent basketball game, Shenille attempted only three-point shots and two-point shots. She was successful on 20% of her three-point shots and 30% of her two-point shots. Shenille attempted 30 shots. How many points did she score?
(A) 12
(B) 18
(C) 24
(D) 30
(E) 36
fuel efficiency of manual and automatic cars, part i. each year the us environmental protection agency (epa)releases fuel economy data on cars manufactured in that year. below are summary statistics on fuel efficiency (in miles/gallon) from random samples of cars with manual and automatic transmissions. do these data provide strong evidence of a difference between the average fuel efficiency of cars with manual and automatic transmissions in terms of their average city mileage? assume that conditions for inference are satisfied.
Answers
Given the above prompt on hypothesis testing, we can state that specifically, cars with manual transmissions have a significantly higher average city mileage than those with automatic transmissions.
What is the explanation for the above response?
To determine if there is strong evidence of a difference between the average fuel efficiency of cars with manual and automatic transmissions in terms of their average city mileage, we can conduct a two-sample t-test assuming unequal variances. The null hypothesis is that there is no difference in the average city mileage between the two types of transmissions, and the alternative hypothesis is that there is a difference.
The t-test statistic is calculated as follows:
t = (x1 - x2) / sqrt((s1^2/n1) + (s2^2/n2))
where x1 and x2 are the sample means, s1 and s2 are the sample standard deviations, and n1 and n2 are the sample sizes.
Plugging in the values from the given statistics, we get:
t = (16.12 - 19.85) / sqrt((3.85^2/26) + (4.51^2/26))
t = -3.31
Using a significance level of 0.05 and 50 degrees of freedom (approximated by n1+n2-2), the critical t-value is ±2.01.
Since the calculated t-value (-3.31) is less than the critical t-value, we can reject the null hypothesis and conclude that there is strong evidence of a difference between the average fuel efficiency of cars with manual and automatic transmissions in terms of their average city mileage.
Specifically, cars with manual transmissions have a significantly higher average city mileage than those with automatic transmissions.
Learn more about hypothesis testing at:
https://brainly.com/question/30588452
#SPJ1
Full Question:
Although part of your question is missing, you might be referring to this full question: See attached image.
6. ____ tales and _____ tales
folk tales are storues with no known creator. they were originally passed down from one generation to another by word of mouth.
fairytales were often created to teach children behavior in an entertaining way.
what is the blank fictions/nonfictions?
Answers
The complete statement is folk tales and fairy tales
Both folk tales and fairy tales are types of fiction because they are imaginative stories that are not based on factual events or characters.
Explaining fictions and nonfictions?Folk tales
Folk tales are stories with no known creator. They were originally passed down from one generation to another by word of mouth. Folk tales are a type of traditional literature that is deeply rooted in the culture of a particular region or community.
They often feature supernatural elements, and their origins can be traced back many centuries.
Because they were passed down orally, different versions of the same tale may have developed in different regions, with variations in characters, plot, and theme.
Fairy tales
Fairy tales were often created to teach children behavior in an entertaining way. Fairy tales are a type of story that typically features magical creatures or events and often have a moral or lesson to teach. They were originally intended for both adults and children and were used as a way to teach moral values, societal norms, and important life lessons in an entertaining way.
The fairy tale genre has evolved over time, and modern fairy tales may have different themes and messages than traditional ones.
Read more about tales at
https://brainly.com/question/28929179
#SPJ1
pls pls help. just need the answer
Answers
The value of k is given as follows:
k = 5.
How to obtain the value of k?The function in the context of this problem is defined as follows:
f(x) = x³ + kx - 6.
We have that x - 1 is a factor of the function, meaning that, by the Factor Theorem:
f(1) = 0, x - 1 = 0 -> x = 1.
Hence, applying the numeric value, the value of k is obtained as follows:
1 + k - 6 = 0
k - 5 = 0
k = 5.
More can be learned about the Factor Theorem at https://brainly.com/question/24729294
#SPJ1
Circle A has radius AB and Circle X has radius XY. Points A and X are distinct points. Complete the statements below describing how to prove that the circles are similar.
Translate the center of circle A onto point __ __.
Then dilate the image of circle A about its center by a scale factor of __ __.
Answers
Translate the center of circle A onto point X.Then dilate the image of circle A about its center by a scale factor of XY/AB.
What is circle?A circle is a geometric shape consisting of points in a plane that are equidistant from a fixed point called the center, forming a closed curve.
According to the given information :
To prove that circles A and X are similar, we can follow the steps below:
1) Translate the center of circle A onto point X. This can be done by moving the center of circle A to point X while keeping the radius AB the same.
2) Dilate the image of circle A about its center by a scale factor of XY/AB. This means that we multiply the radius of the image of circle A by XY/AB. The result is a new circle that is similar to circle A and has the same center as circle X.
To summarize, the statements to complete are:
Translate the center of circle A onto point X.
Then dilate the image of circle A about its cent er by a scale factor of XY/AB.
To know more about Circle visit :
https://brainly.com/question/11833983
#SPJ1
Translate the center of circle A onto point X.Then dilate the image of circle A about its center by a scale factor of XY/AB.
What is circle?
A circle is a geometric shape consisting of points in a plane that are equidistant from a fixed point called the center, forming a closed curve.
According to the given information :
To prove that circles A and X are similar, we can follow the steps below:
1) Translate the center of circle A onto point X. This can be done by moving the center of circle A to point X while keeping the radius AB the same.
2) Dilate the image of circle A about its center by a scale factor of XY/AB. This means that we multiply the radius of the image of circle A by XY/AB. The result is a new circle that is similar to circle A and has the same center as circle X.
To summarize, the statements to complete are:
Translate the center of circle A onto point X.
Then dilate the image of circle A about its center by a scale factor of XY/AB.
To know more about Circle visit :
https://brainly.com/question/11833983
#SPJ1
Solve the following problem. Be sure to show all the steps (V. E. S. T. ) and work in order to receive full credit.
The sum of three numbers is 26. The second number is twice the first and the third number is 6 more than the second. Find the numbers.
Please help due tomorrow
Answers
The three numbers are 4, 8, and 14.
Let's use variables to represent the three numbers
Let x be the first number.
Then the second number is twice the first, so it is 2x.
The third number is 6 more than the second, so it is 2x + 6.
We know that the sum of the three numbers is 26, so we can write an equation:
x + 2x + (2x + 6) = 26
Now we can solve for x
5x + 6 = 26
5x = 20
x = 4
So the first number is 4.
To find the second number, we can use the equation we wrote earlier:
2x = 2(4) = 8
So the second number is 8.
To find the third number, we can use the other equation we wrote earlier
2x + 6 = 2(4) + 6 = 14
So the third number is 14.
Learn more about equation here
brainly.com/question/14603452
#SPJ4
a slide caliper has 32 divisions per inch and a vernier of 8 divisions per major division. for this instrument the smallest resolution and uncertainty are:
Answers
The smallest resolution for this instrument is 1/256 inches.
This is also the instrument's uncertainty, as it represents the smallest measurable increment.
Let's first understand the terms mentioned:
Slide caliper:
A measuring instrument with a main scale and a vernier scale for taking precise measurements.
Divisions per inch:
The number of equal divisions on the main scale in one inch.
Vernier:
A short auxiliary scale that slides along the main scale, allowing for more precise readings.
Divisions per major division:
The number of equal divisions on the vernier scale that correspond to one division on the main scale.
Now, let's determine the smallest resolution and uncertainty for this instrument.
Calculate the main scale resolution
Main scale resolution = 1 inch / 32 divisions per inch = 1/32 inches
Calculate the vernier scale resolution
Vernier scale resolution = Main scale resolution / Vernier divisions per major division = (1/32 inches) / 8 = 1/256 inches.
For similar question on resolution.
https://brainly.com/question/30557183
#SPJ11
three machines, a, b, c produce a large number of identical products. 60% of the products come from machine a, 30% from b and 10% from c. historical records indicate that 10% of the parts produced by machine a are defective, compared with 30% for machine b and 40% for machine c. what is the probability that a randomly chosen part is defective?
Answers
The probability that a randomly chosen part is defective is 0.16, or 16%.
The probability that a randomly chosen part is defective, we need to use the law of total probability.
Let [tex]$D$[/tex] be the event that a part is defective and let [tex]$M_i$[/tex] be the event that the part came from machine [tex]$i$[/tex], for [tex]$i = A, B, C$[/tex].
Then we have:
[tex]$P(D) = P(D|M_A)P(M_A) + P(D|M_B)P(M_B) + P(D|M_C)P(M_C)$[/tex]
60% of the products come from machine A, 30% from machine B, and 10% from machine C.
Therefore:
[tex]$P(M_A) = 0.6$[/tex]
[tex]$P(M_B) = 0.3$[/tex]
[tex]$P(M_C) = 0.1$[/tex]
The probability of a part being defective is 10% if it comes from machine A, 30% if it comes from machine B, and 40% if it comes from machine C.
Therefore:
[tex]$P(D|M_A) = 0.1$[/tex]
[tex]$P(D|M_B) = 0.3$[/tex]
[tex]$P(D|M_C) = 0.4$[/tex]
Substituting these values into the law of total probability, we get:
[tex]$P(D) = 0.1 \cdot 0.6 + 0.3 \cdot 0.3 + 0.4 \cdot 0.1 = 0.16$[/tex]
For similar questions on randomly
https://brainly.com/question/24140969
#SPJ11
Eli's house is due west of Yardley and due south of Salem. Yardley is 7 miles from Eli's house and 9 miles from Salem. How far is Salem from Eli's house, measured in a straight line? If necessary, round to the nearest tenth
Answers
By Pythagorean , Eli's home is thus roughly **11.4 miles** from Salem when viewed from a straight line.
Define Pythagorean theorem?A fundamental relationship between a right triangle's three sides in Euclidean geometry is known as the Pythagorean theorem. The hypotenuse is the side that forms the right angle, and the rule says that the square of its length is equal to the sum of the squares of the lengths of the other two sides. In other words, if the hypotenuse is length c and the legs of a right triangle are lengths a and b, then a²+ b² = c² .
Call Yardley Y, Salem S, and Eli's home E. As far as we are aware, Y is located 7 miles from E and 9 miles from S.
We can check that the distance between Eli's house and Salem is the hypotenuse of a right triangle with Yardley as one of the vertices because Eli's house is located due west of Yardley and due south of Salem. The Pythagorean theorem can be used to determine this distance.
Eli's home is 11.4 miles from Salem at a distance of√(7 + 9 ) = √(130).
√(130) = 11.4miles
Eli's home is thus roughly **11.4 miles** from Salem when viewed from a straight line.
To know more about Pythagorean theorem visit:
brainly.com/question/14930619
#SPJ1
HELP PLS EXPLAIN THISSSSS
Answers
Plugging in the values given into the expression, and simplifying, we would have our answer as: B. [tex]\frac{9}{25}[/tex]
How to Evaluate an Expression?To evaluate an expression, follow these steps:Identify the variables and constants in the expression.Substitute the given values for each variable in the expression.Simplify the expression until there are no more operations left.Given that, a = 5 and k = -2, substitute the values into the expression given and simplify:
[tex](\frac{3^2(5^{-2})}{3(5^{-1})} )^{-2}[/tex]
Simplify:
[tex](\frac{9 * \frac{1}{25} }{3* \frac{1}{5} } )^{-2}[/tex]
[tex](\frac{\frac{9}{25} }{\frac{3}{5} } )^{-2}\\\\(\frac{9}{25} * \frac{5}{3} } )^{-2}\\\\(\frac{3}{5} )^{-2}\\\\ = \frac{9}{25}[/tex]
Learn more about value of an expression on:
https://brainly.com/question/625174
#SPJ1
Evaluate the expression when x = 7 (4x + 9) - 4(x - 1) + x use the answer choices in the diagram
Answers
Answer:
The answer is 20
Step-by-step explanation:
when x=7
(4x+9)-4(x-1)+x
(4(7)+9)-4(7-1)+7
28+9 -4(6)+7
37+7-24
44-24
=20
a plumber works twice as fast as his apprentice. after the plumber has worked alone for 3 hours, his apprentice joins him and working together they complete the job 4 hours later. how many hours would it have taken the plumber to do the entire job by himself?
Answers
If after the plumber has worked alone for 3 hours, his apprentice joins him and working together they complete the job 4 hours later, it would take the plumber 9 hours to do the entire job by himself.
Let's start by assigning some b to represent the rate at which each person works. Let's say that the plumber's rate is P (in units of job per hour) and the apprentice's rate is A (also in units of job per hour). Since the plumber works twice as fast as the apprentice, we can write:
P = 2A
Next, let's think about how much work can be done in a certain amount of time. If the plumber works alone for 3 hours, he completes 3P units of work. When the apprentice joins him, they work together for another 4 hours to complete the entire job, which is a total of 7 hours of work. So, the amount of work done in those 4 hours is:
4(P + A)
We also know that the total amount of work is 1 (since it's one complete job). Putting this all together, we can write an equation:
3P + 4(P + A) = 1
We can simplify this to:
7P + 4A = 1
But we also know that P = 2A, so we can substitute that in:
7(2A) + 4A = 1
Simplifying this, we get:
18A = 1
So, A = 1/18. This means that the apprentice can complete 1/18 of the job in one hour. Since the plumber works twice as fast, he can complete 2/18 of the job (or 1/9) in one hour.
To find out how long it would take the plumber to do the entire job by himself, we can use the formula:
Time = Work / Rate
The entire job is 1, and the plumber's rate is 1/9. So:
Time = 1 / (1/9) = 9 hours
To learn more about time and work click on,
https://brainly.com/question/15447600
#SPJ4
the random variable x is the number of occurrences of an event over an interval of 10 minutes. it can be assumed the probability of an occurrence is the same in any two time periods of an equal length. it is known that the mean number of occurrences in 10 minutes is 5.3. the probability there are 8 occurrences in 10 minutes is . a. .0771 b. .0241 c. .1126 d. .9107
Answers
The probability of having 8 occurrences in 10 minutes is approximately 0.0241, which means the answer is (b).
The number of occurrences of an event in 10 minutes as a Poisson distribution with mean lambda = 5.3.
The probability of having 8 occurrences in 10 minutes is:
[tex]P(X = 8) = (e^(-5.3) * 5.3^8) / 8![/tex]
where X is the random variable representing the number of occurrences of the event in 10 minutes.
Using a calculator, we can evaluate this expression:
[tex]P(X = 8) = (e^(-5.3) * 5.3^8) / 8! ≈ 0.0241[/tex]
for such more questions on random variable
https://brainly.com/question/17217746
#SPJ11
The volume of a cylinder is given by the formula v - pi^h, where r is the radius of the cylinder and h is the height.
Which expression represents the volume of this cylinder?
Answers
The expression that represents the volume of the cylinder is:
V = π[tex]r^{2}[/tex]h
What is cylinder?
A cylinder is a three-dimensional geometric shape that consists of two parallel circular bases of the same size and shape, and a curved lateral surface connecting the bases. The cylinder can be thought of as a tube or a can. The lateral surface of the cylinder is formed by "unrolling" a rectangular shape along the circumference of the base.
There appears to be a typographical error in the given formula for the volume of a cylinder. The correct formula is:
V = π[tex]r^{2}[/tex]h
where V is the volume of the cylinder, r is the radius of the circular base, and h is the height of the cylinder.
Using this formula, the expression that represents the volume of the cylinder is:
V = π[tex]r^{2}[/tex]h
To learn more about cylinder from the given link:
https://brainly.com/question/16134180
#SPJ1
What are the cross-products of the proportion 6/40 = 9/60? Is the proportion TRUE?
54 and 2,400; the proportion is false.
54 and 540; the proportion is true.
360 and 360; the proportion is true.
Answers
Therefore, the answer is: 360 and 360; the proportion is true.
54 and 540; the proportion is true.
360 and 360; the proportion is true.
To find the cross-products of the proportion 6/40 = 9/60, we multiply the numerator of the first fraction by the denominator of the second fraction, and the numerator of the second fraction by the denominator of the first fraction.
So we have:
6 × 60 = 360
9 × 40 = 360
The cross-products are 360 and 360.
To check if the proportion is true, we compare the cross-products. If they are equal, then the proportion is true; otherwise, it is false.
Since the cross-products are equal, the proportion is true.
Therefore, the answer is:
360 and 360; the proportion is true.
To know more about fraction visit:
https://brainly.com/question/10354322
#SPJ1
The data for the height and weight of different people was collected the line of best fit for this date it was determined to be Y equals 0. 9 1X -65. 5 where X is the height in centimeters and why is the weight in kilograms is in the equation predict the height of a person who weighs 63 kg
Answers
According to the equation, a person who weighs 63 kg is predicted to be approximately 141 centimeters tall.
The equation given is Y = 0.91X - 65.5, where X represents the height in centimeters and Y represents the weight in kilograms. To predict the height of a person who weighs 63 kg, we need to solve for X, the height in centimeters.
To do this, we can plug in the given weight of 63 kg for Y in the equation and then solve for X. So, we have:
63 = 0.91X - 65.5
Adding 65.5 to both sides, we get:
63 + 65.5 = 0.91X
Simplifying, we have:
128.5 = 0.91X
Finally, to solve for X, we divide both sides by 0.91, giving:
X = 141.21
To know more about equation here
https://brainly.com/question/10413253
#SPJ4
Find the volume of the prism.
The volume is
cubic feet.
Answers
Answer: 8/125 or 0.064
Step-by-step explanation:
volume of a cube is w^3
(2/5)*(2/5)*(2/5)
8/125 or 0.064
Given the following code fragment, which of the following expressions is always true?
int x;
scanf("%d", &x);
A) if( x = 1)
B) if( x < 3)
C) if( x == 1)
D) if((x/3) > 1)
Answers
If the expressions given, only C) if( x == 1) is always true.
In the given code fragment, the value of x is read from the user using the scanf() function. The value of x can be any integer value, depending on what the user enters. After the value of x is read, the program checks the value of x using a conditional statement (if statement) and executes the code inside the if statement only if the condition is true.
Expression A) if( x = 1) assigns the value 1 to x and then checks if x is true. This means that the condition is always true, because the assignment operation (=) returns the assigned value (in this case, 1), which is a non-zero value and therefore considered true in C programming.
Expression B) if( x < 3) checks if x is less than 3. This expression is not always true, as x can be any value greater than or equal to 3, in which case the condition would be false.
Expression C) if( x == 1) checks if x is equal to 1. This expression is always true if the user enters the value 1 for x.
Expression D) if((x/3) > 1) checks if the integer division of x by 3 is greater than 1. This expression is not always true, as x can be any value less than or equal to 3, in which case the result of the integer division by 3 would be 1 or less, in which case the condition would be false.
Learn more about expressions
https://brainly.com/question/14083225
#SPJ4
the only expression that is always true in this code fragment is option C) if( x == 1).
The expression that is always true in this code fragment is option C) if( x == 1).
Option A) if( x = 1) is not always true because it is an assignment statement instead of a comparison statement. It assigns the value 1 to x instead of checking if x is equal to 1.
Option B) if( x < 3) is also not always true because x could be any number less than 3.
Option D) if((x/3) > 1) is not always true because x could be any number less than or equal to 3, in which case the expression would evaluate to false.
Therefore, the only expression that is always true in this code fragment is option C) if( x == 1).
learn more about code fragment
https://brainly.com/question/31133611
#SPJ11
What is the slope of the line?
-2
-1
1
2
Answers
Answer: positive 2
Step-by-step explanation:
As a nurse working in a hospital one of the jobs is to give appropriate doses of medicine
before surgery so the patient doesn't wake up during surgery. 4cc of this particular medicine is
meant for a 180lb man, what would be the correct dosage for a 145 lb. woman?
Answers
Answer:
the correct dosage of the medicine for a 145 lb. woman would be approximately 3.22 cc
Step-by-step explanation:
To calculate the correct dosage of the medicine for a 145 lb. woman, we can use the following formula:
dosage = (weight of patient / weight of reference patient) x reference dosage
where the weight of the reference patient is 180 lb. and the reference dosage is 4 cc.
Plugging in the given values, we get:
dosage = (145 / 180) x 4
= 3.22 cc (rounded to two decimal places)
Therefore, the correct dosage of the medicine for a 145 lb. woman would be approximately 3.22 cc. However, it's important to note that dosages of medications should only be determined by a qualified medical professional based on a number of factors, including the patient's weight, medical history, and current condition.
call a positive integer kinda-prime if it has a prime number of positive integer divisors. if there are $168$ prime numbers less than $1000$, how many kinda-prime positive integers are there less than $1000$?
Answers
There are 173 kinda-prime positive integer less than 1000.
To find the number of kinda-prime positive integer less than 1000, we'll follow these steps:
1. Understand the definition of a kinda-prime number: A positive integer is kinda-prime if it has a prime number of positive integer divisors.
2. Determine the number of prime numbers less than 1000: There are 168 prime numbers less than 1000, as given.
3. Determine the possible prime number of divisors: Since 168 is not too large, we only need to consider 2 and 3 as possible prime numbers of divisors for a kinda-prime number.
4. Analyze the cases:
Case 1: Kinda-prime numbers with 2 divisors (prime numbers)
All prime numbers have exactly 2 divisors (1 and itself). Thus, all 168 prime numbers less than 1000 are kinda-prime.
Case 2: Kinda-prime numbers with 3 divisors
Let N be a kinda-prime number with 3 divisors. Then, N = p^2 for some prime number p. To find the suitable prime numbers p, we need[tex]p^2 < 1000[/tex]. The prime numbers that meet this condition are 2, 3, 5, 7, and 11 (since 13^2 = 169 > 1000). Therefore, there are 5 additional kinda-prime numbers ([tex]2^2, 3^2, 5^2, 7^2, and 11^2[/tex]).
5. Add the total number of kinda-prime numbers from both cases: 168 + 5 = 173.
Learn more about integer here:
https://brainly.com/question/17118150
#SPJ11
[tex]$(\pi(1000)-1)+11=\boxed{177}$[/tex] "kind a-prime" positive integers less than $1000$.
Let [tex]$n$[/tex] be a positive integer with[tex]$k$[/tex] positive integer divisors.
If [tex]$k$[/tex] is prime, then.
[tex]$n$[/tex] is a "kind a-prime" integer.
[tex]$k$[/tex] must be of the form.
[tex]$k=p$[/tex] or [tex]$k=p^2$[/tex] for some prime [tex]$p$[/tex].
If [tex]$k=p$[/tex], then [tex]$n$[/tex] must be of the form.
[tex]$p^{p-1}$[/tex] for some prime [tex]$p$[/tex]. Since [tex]$p < 1000$[/tex], there are.
[tex]$\pi(1000)$[/tex]possible values of [tex]$p$[/tex].
[tex]$p=2$[/tex] gives [tex]$2^1$[/tex], which is not prime, so we have to subtract.
[tex]$1$[/tex] from [tex]$\pi(1000)$[/tex] to get the number of possible.
[tex]$p$[/tex].
[tex]$\pi(1000)-1$[/tex] values of [tex]$p$[/tex] that give a "kind a-prime" integer of this form.
If [tex]$k=p^2$[/tex], then [tex]$n$[/tex] must be of the form.
[tex]$p^{p^2-1}$[/tex] for some prime[tex]$p$[/tex].
There are.
[tex]$\pi(31)=11$[/tex] primes less than [tex]$31$[/tex], and each of them gives a different "kind a-prime" integer of this form.
Since [tex]$31^5 > 1000$[/tex], no primes larger than [tex]$31$[/tex]can be used to form a "kind a-prime" integer of this form.
[tex]$11$[/tex] possible values of [tex]$p$[/tex] that give a "kind a-prime" integer of this form.
For similar questions on Positive Integer
https://brainly.com/question/16952898
#SPJ11
What is the argument of z = StartFraction 1 Over 16 EndFraction minus StartFraction StartRoot 3 EndRoot Over 16 EndFraction i?
Answers
To find the argument of the complex number z = 1/16 - (sqrt(3)/16)i, we need to find the angle that the complex number forms with the positive real axis in the complex plane.
We can start by finding the magnitude of z, which is the distance between the origin and the point representing z in the complex plane:
|z| = sqrt( (1/16)^2 + (sqrt(3)/16)^2 )
= sqrt(1/256 + 3/256)
= sqrt(4/256)
= 1/4
Next, we can find the argument of z using the formula:
arg(z) = tan^(-1)(Im(z)/Re(z))
where Im(z) is the imaginary part of z, and Re(z) is the real part of z.
In this case, we have:
Re(z) = 1/16
Im(z) = -(sqrt(3)/16)
Therefore, we get:
arg(z) = tan^(-1)(Im(z)/Re(z))
= tan^(-1)(-(sqrt(3)/16)/(1/16))
= tan^(-1)(-sqrt(3))
= -60° (in degrees)
So, the argument of z is -60 degrees (or -π/3 radians).
Answer:
A
Step-by-step explanation:
From a horizontal distance of 80.0 m, the angle to the top of a flagpole is 18°. Calculate the height of the flagpole to the nearest tenth of a meter.
1. 24.7 meters
2. 76.1 meters
3. 26.0 meters
4. 25.3 meters
Answers
Answer:
The figure is omitted--please sketch it to confirm my answer.
Set your calculator to degree mode.
Let h be the height of the flagpole.
[tex] \tan(18) = \frac{h}{80} [/tex]
[tex]h = 80 \tan(18) = 25.994[/tex]
The height of the flagpole is approximately 26.0 meters. #3 is correct.
A rectangular plece of paper with length 28 cm and width 14 cm has two semicircles cut out of it, as shown below. Find the area of the paper that remains. Use the value 3.14 for 1, and do not round your answer. G ✓6 14 cm 0 00 H cm X 2023 McGraw Hill LLC As Rights Reserve
Answers
The area of the paper remains is 238.14 cm².
What is area?Area is the region bounded by a plane shape.
To calculate the area of the paper that remains, we use the formula below.
Formula:
Area of the paper that remains(A) = Area of the rectangle(LW)-Area of the two semi circles [π(W/2)²]A = LW- [π(W/2)²]................ Equation 1Where:
L = Length of the rectangleW = Width of the rectangle = Diameter of the semi circleFrom the diagram in the question,
Given:
L = 28 cmW = 14 cmSubstitute these values into equation 1
A = (28×14)-[3.14(14/2)²A = 392-153.86A = 238.14 cm²Hence, the area is 238.14 cm².
Learn more about area here: https://brainly.com/question/28470545
#SPJ1
Gemma can't type 350 words in five minutes how many words can she type in 3/4 of an hour
Answers
Answer:
Gemma can type 3150 words in 3/4hr
Step-by-step explanation:
350 word------>five minutes
x words------->3/4hr
convert 3/4hr-minutes
3/4×60=45minutes
x word =350×45/5
x word=3,150 words
For the first half of a baseball season, a player had 90 hits out of 270 times at bat. The player's batting average was
90
270
≈ 0. 333. During the second half of the season, the player had 64 hits out of 276 times at bat. The player's batting average was
64
276
≈ 0. 232. (Round your answers to three decimal places. )
(a) What is the average (mean) of 0. 333 and 0. 232?
Answers
The issue inquires to discover the normal (cruel) of two values:
0.333 and 0.232. To do this, able to essentially include the two values together and partition them by 2. Including the two values gives us:
0.333 + 0.232 = 0.565
Separating by 2 gives us:
0.565 / 2 = 0.2825
So the normal of 0.333 and 0.232 is 0.2825.
In any case, the issue inquires to circular our answer to three decimal places, which suggests we have to be circular 0.2825 to the closest thousandth. The third decimal put maybe a 2, which implies we circular down. Hence, the ultimate reply is roughly 0.283, adjusted to three decimal places.
To learn about partition visit:
https://brainly.com/question/30191477
#SPJ4