Answers
Step by step
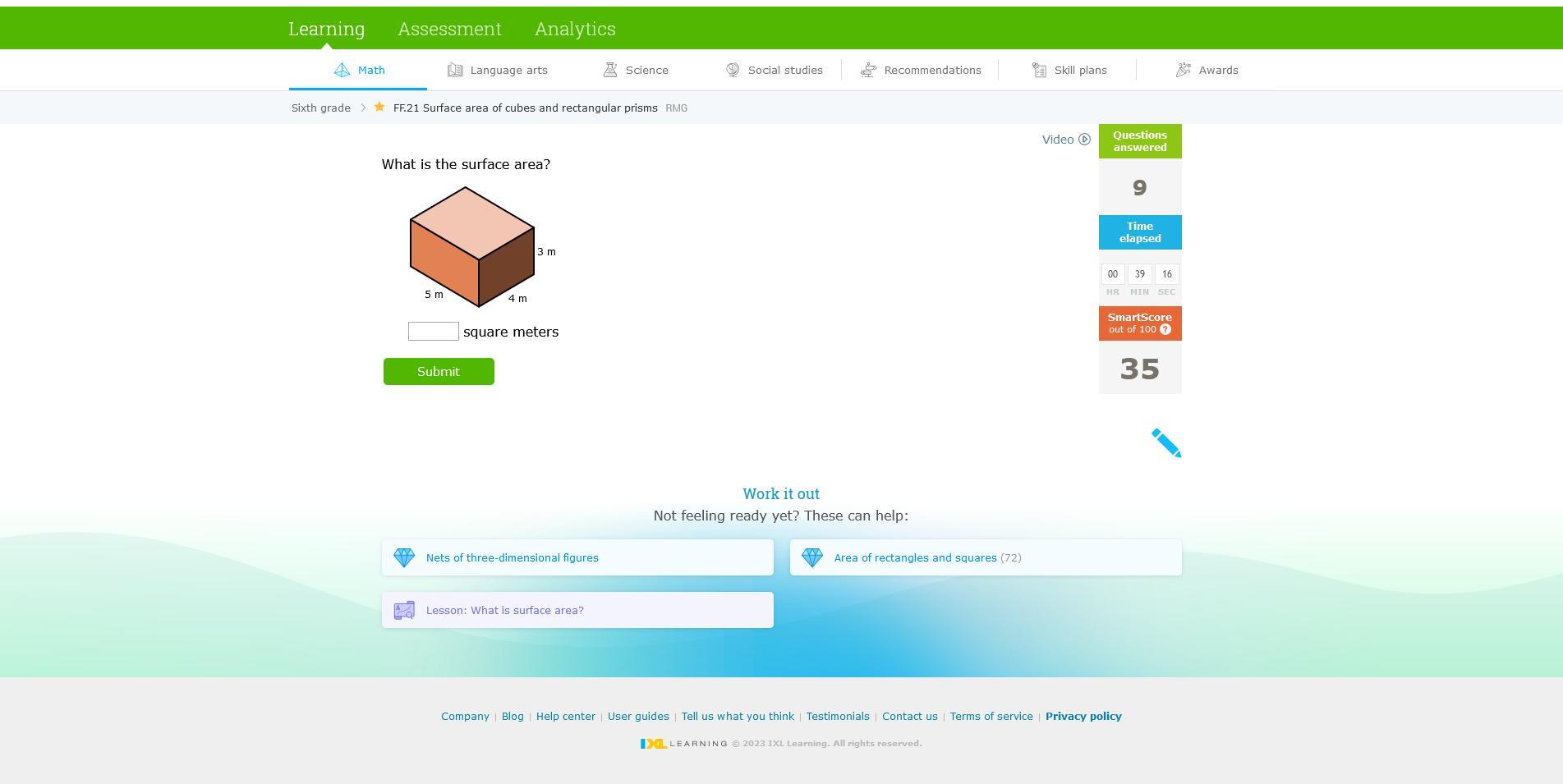
Our rectangular box is 3 x 4 x 5 meters
We know area A = L x W
We know the box has a top and bottom, two long sides and two end sides for a total of 6 sides
Top and bottom 2 sides x 4 x 5 = 40
Two long sides 2 sides x 3 x 5 = 30
Two end sides 2 sides x 3 x 4 = 24
Add together for a total surface area 94m^2
Answer: 94 square inches 2
Step-by-step explanation:
2×(5×4 + 5×3 + 4×3) = 94 sq in 2
length x width x height
if you need more help with your ixl I am free to help!
have a good day!
Related Questions
When adding or subtracting mixed numbers with like denominators, the numerators ___ , but the denominators ______ .
A. Stay the same
B. change
Answers
Answer:
Yo, when you adding or subtracting mixed numbers with the same denominators, the numerators stay chill, they don't change, bro.
But the denominators, they also stay the same, man. It's like keeping things consistent, ya feel me? So the answer is A, dude. Numerators stay put, denominators stay put. It's all good vibes, bro! ✌️
If you watch from ground level, a child riding on a merry-go-round will seem to be undergoing simple harmonic motion from side to side. Assume the merry-go-round is 10.6 feet across and the child completes 8 rotations in 120 seconds. Write a sine function that describes d, the child's apparent distance from the center of the merry-go-round, as a function of time t.
Answers
The sine function that describes the child's apparent distance from the center of the merry-go-round is d(t) = 5.3 sin(2π/15 * t)
How to write a sine function that describes the child's apparent distance?To write a sine function that describes the child's apparent distance from the center of the merry-go-round as a function of time t, we can start by finding the amplitude, period, and phase shift of the motion.
Amplitude:
The amplitude of the motion is half the diameter of the merry-go-round, which is 10.6/2 = 5.3 feet. This is because the child moves back and forth across the diameter of the merry-go-round.
Period:
The period of the motion is the time it takes for the child to complete one full cycle of back-and-forth motion, which is equal to the time it takes for the merry-go-round to complete one full rotation.
From the given information, the child completes 8 rotations in 120 seconds, so the period is T = 120/8 = 15 seconds.
Phase shift:
The phase shift of the motion is the amount of time by which the sine function is shifted horizontally (to the right or left).
In this case, the child starts at one end of the diameter and moves to the other end, so the sine function starts at its maximum value when t = 0. Thus, the phase shift is 0.
With these values, we can write the sine function that describes the child's apparent distance from the center of the merry-go-round as:
d(t) = 5.3 sin(2π/15 * t)
where d is the child's distance from the center of the merry-go-round in feet, and t is the time in seconds. The factor 2π/15 is the angular frequency of the motion, which is equal to 2π/T.
Learn more about sine function on:
https://brainly.com/question/30243373
#SPJ1
A rock of radioactive material has 500 atoms in it. The number of atoms decreases at a rate of 11% a day. Write an exponential function that models this situation. f(x) type your answer... (1 choose your answer... choose your answer... ✓)^x
Answers
Answer:
[tex]f(x) = 500( {.89}^{x} )[/tex]
Solve Triangle
Because I Need Answer My Assignment:-)
Good Perfect Complete=Brainlist
Copy Wrong Incomplete=Report
Good Luck Answer Brainly Users:-)
Answers
Answer:
x = 4√5 ≈ 8.94 (2 d.p.)
y = 8√5 ≈ 17.89 (2 d.p.)
Step-by-step explanation:
To find the values of x and y, use the Geometric Mean Theorem (Leg Rule).
Geometric Mean Theorem (Leg Rule)The altitude drawn from the vertex of the right angle perpendicular to the hypotenuse separates the hypotenuse into two segments. The ratio of the hypotenuse to one leg is equal to the ratio of the same leg and the segment directly opposite the leg.
[tex]\boxed{\sf \dfrac{Hypotenuse}{Leg\:1}=\dfrac{Leg\:1}{Segment\;1}}\quad \sf and \quad \boxed{\sf \dfrac{Hypotenuse}{Leg\:2}=\dfrac{Leg\:2}{Segment\;2}}[/tex]
From inspection of the given right triangle RST:
Altitude = SVHypotenuse = RT = 20Leg 1 = RS = ySegment 1 = RV = 16Leg 2 = ST = xSegment 2 = VT = 4Substitute the values into the formulas:
[tex]\boxed{\dfrac{20}{y}=\dfrac{y}{16}}\quad \sf and \quad \boxed{\dfrac{20}{x}=\dfrac{x}{4}}[/tex]
Solve the equation for x:
[tex]\implies \dfrac{20}{x}=\dfrac{x}{4}[/tex]
[tex]\implies 4x \cdot \dfrac{20}{x}=4x \cdot \dfrac{x}{4}[/tex]
[tex]\implies 80=x^2[/tex]
[tex]\implies \sqrt{x^2}=\sqrt{80}[/tex]
[tex]\implies x=\sqrt{80}[/tex]
[tex]\implies x=\sqrt{4^2\cdot 5}[/tex]
[tex]\implies x=\sqrt{4^2}\sqrt{5}[/tex]
[tex]\implies x=4\sqrt{5}[/tex]
Solve the equation for y:
[tex]\implies \dfrac{20}{y}=\dfrac{y}{16}[/tex]
[tex]\implies 16y \cdot \dfrac{20}{y}=16y \cdot \dfrac{y}{16}[/tex]
[tex]\implies 320=y^2[/tex]
[tex]\implies \sqrt{y^2}=\sqrt{320}[/tex]
[tex]\implies y=\sqrt{320}[/tex]
[tex]\implies y=\sqrt{8^2\cdot 5}[/tex]
[tex]\implies y=\sqrt{8^2}\sqrt{5}[/tex]
[tex]\implies y=8\sqrt{5}[/tex]
Solve for X, please write an explanation.
Answers
Step-by-step explanation:
2x+20 and 2x-4 are supplementary angles...they form a straight line and thus = 180 degrees when added together
2x+20 + 2x-4 = 180 simplify
4x + 16 = 180 subtract 16 from both sides
4x = 164 divide both sides by 4
x = 41 degrees
When x is 2, what is the value of the expression 124+3(8−x)12
12
4
+
3
(
8
−
x
)
12
?
Answers
When x is 2, the value of the expression is 9.
Describe Algebraic Expression?An algebraic expression is a mathematical phrase that contains one or more variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. It can also contain exponents, roots, and trigonometric functions.
Algebraic expressions are used to represent mathematical relationships and solve problems in a wide range of fields, including physics, engineering, finance, and statistics. They can be used to model real-world phenomena and to make predictions based on data.
Algebraic expressions can be simplified by combining like terms and using mathematical rules and properties. They can also be evaluated by substituting values for the variables and simplifying the expression. Solving equations involving algebraic expressions often involves manipulating the expression to isolate a variable and find its value.
When x is 2, the value of the expression 12/4+3(8−x)-12 can be found by substituting 2 for x and simplifying the expression:
12/4 + 3(8 - 2) - 12
= 3 + 3(6) - 12
= 3 + 18 - 12
= 9
Therefore, when x is 2, the value of the expression is 9.
To know more about expression visit:
https://brainly.com/question/15813344
#SPJ1
The complete question is :
When x is 2, what is the value of the expression 12/4+3(8−x)-12?
Select the correct answer. Sides of three square rooms measure 14 feet each, and sides of two square rooms measure 17 feet each. Which expression shows the total area of these five rooms? A. (3 × 14^2) + (2 × 17^2) B. (2 × 14^3) + (2 × 17^2) C. (3 × 17^2) + (2 × 14^2) D. (3 × 14^2) × (2 × 17^2) Reset Next
Answers
The correct expression showing the total area of the five rooms is A. (3 x 14²) + (2 x 17²), which simplifies to 1918 square feet.
What is expression?An expression is a combination of numbers, symbols, and operators (such as addition, subtraction, multiplication, and division) that represent a mathematical calculation. An expression can be a single number, a variable, or a combination of both, and can be used to represent mathematical formulas, equations, or relationships.
In the given question,
C. (3 × 17²) + (2 × 14²)
To find the total area of the five rooms, we need to add the area of each room. The area of a square is found by squaring the length of one side.
For the three rooms with sides of 14 feet each, the area of each room is:
14^2 = 196 square feet
So the total area of these three rooms is:
3 × 196 = 588 square feet
For the two rooms with sides of 17 feet each, the area of each room is:
17^2 = 289 square feet
So the total area of these two rooms is:
2 × 289 = 578 square feet
Therefore, the total area of all five rooms is:
588 + 578 = 1166 square feet
Option C, (3 × 17²) + (2 × 14²), gives the correct expression for this calculation.
To know more about expression, visit:
https://brainly.com/question/2559684
#SPJ1
April is considering a 7/23 balloon mortgage with an interest rate of 4.15% to
purchase a house for $197,000. What will be her balloon payment at the end
of 7 years?
OA. $173,819.97
OB. $170,118.49
OC. $225,368.29
OD. $170,245.98
SUBMIT
Answers
The balloon payment at the end of 7 years would be $173,819.97, which is option A.
How to find the balloon payment at the end of 7 yearsA 7/23 balloon mortgage means that April will make payments on the loan as if it were a 23-year mortgage, but the remaining balance of the loan will be due in full after 7 years.
To find the balloon payment at the end of 7 years, we can first calculate the monthly payment using the loan amount, interest rate, and loan term:
n = 23 * 12 = 276 (total number of payments)
r = 4.15% / 12 = 0.003458 (monthly interest rate)
P = (r * PV) / (1 - (1 + r)^(-n))
where
PV is the present value of the loan (the loan amount)n is the total number of paymentsr is the monthly interest ratePV = $197,000
P = (0.003458 * $197,000) / (1 - (1 + 0.003458)^(-276)) = $1,007.14 (monthly payment)
Now we can calculate the remaining balance on the loan after 7 years. Since April is making payments as if it were a 23-year mortgage, she will have made 7 * 12 = 84 payments by the end of the 7th year.
Using the formula for the remaining balance of a loan after t payments:
B = PV * (1 + r)^t - (P / r) * ((1 + r)^t - 1)
Where
B is the remaining balancePV is the initial loan amount r is the monthly interest rateP is the monthly payment t is the number of payments madet = 84 (number of payments made)
B = $197,000 * (1 + 0.003458)^84 - ($1,007.14 / 0.003458) * ((1 + 0.003458)^84 - 1)
B = $173,819.97
Therefore, the balloon payment at the end of 7 years would be $173,819.97, which is option A.
Learn more about monthly payment here : brainly.com/question/28106777
#SPJ1
HELP!! 10 POINTS
uhm yeah thats all I've got to say
Answers
The correct statement regarding the middle 50% of the data-set is given as follows:
C. The box, from 41 to 56.
What does a box-and-whisker plot shows?A box and whisker plots shows these five features from a data-set, listed as follows:
The minimum non-outlier value.The 25th percentile, which is the median of the bottom 50%.The median, which splits the entire data-set into two halfs, the bottom 50% and the upper 50%.The 75th percentile, which is the median of the upper 50%.The maximum non-outlier value.The box, from the 25th percentile of 41 to the 75th percentile of 56, shows the middle 50% of the data-set.
More can be learned about box plots at https://brainly.com/question/12343132
#SPJ1
Find the measures of angle a and B. Round to the
nearest degree.
Answers
The measure of angle A and B is 29° and 61° respectively
What is trigonometric ratio?Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle.
sin(tetha) = opp/hyp
tan(tetha) = opp/adj
cos(tetha) = adj/hyp
The opposite is 6 and the adjascent = 11
Therefore tan (tetha) = 11/6 = 1.833
tetha = tan^-1( 1.833)
= 61°( nearest degree)
The sum of angle in a triangle is 180°
therefore,
angle A = 180-( 61+90)
= 180-151
= 29°
therefore the measure of angle A and B is 29° and 61° respectively.
learn more about trigonometric ratio from
https://brainly.com/question/24349828
#SPJ1
write an integral that quantifies the change in the area of the surface of a cube when its side length quadruples from s unit to 4s units.
Answers
Answer:
Step-by-step explanation:
Let A be the area of the surface of the cube.
When the side length changes from s to 4s, the new area A' can be calculated as:
A' = 6(4s)^2 = 96s^2
The change in area is then:
ΔA = A' - A = 96s^2 - 6s^2 = 90s^2
To find the integral that quantifies the change in area, we can integrate the expression for ΔA with respect to s, from s to 4s:
∫(90s^2)ds from s to 4s
= [30s^3] from s to 4s
= 30(4s)^3 - 30s^3
= 1920s^3 - 30s^3
= 1890s^3
Therefore, the integral that quantifies the change in area of the surface of a cube when its side length quadruples from s units to 4s units is:
∫(90s^2)ds from s to 4s
= 1890s^3 from s to 4s
= 1890(4s)^3 - 1890s^3
= 477,840s^3 - 1890s^3
Maggie spent $18. 00 Of $30. 00 In her wallet which decimal represents the fraction of the $30. 00 Maggie spent
Answers
The decimal that represents the fraction of the $30.00 Maggie spent is 0.6.
Now, let's talk about decimals. Decimals are a way of expressing parts of a whole number in a fraction of 10. For example, 0.5 is the same as 1/2. In your situation, Maggie spent $18.00 out of $30.00. To figure out what decimal represents the fraction of the $30.00 Maggie spent, we need to divide the amount she spent by the total amount she had.
So, we can write this as a fraction:
$18.00 / $30.00
To turn this fraction into a decimal, we divide the numerator (top number) by the denominator (bottom number) using long division or a calculator.
$18.00 / $30.00 = 0.6
Another way to say this is that Maggie spent 60% of the money she had in her wallet.
To know more about decimal here
https://brainly.com/question/9543292
#SPJ4
the average car can go 25 miles on one gallon of gas. You can write an equation to show the relationship between the amount of gas you buy and how far you can travel
Answers
Answer:
Step-by-step explanation:
the inword
If anyone is reading this, rn i would be so flipping happy if u got this for me ive been waiting for so long and got nothing please answer correctly please
Answers
Answer: The answer is A.
Step-by-step explanation: Because I am smart don't underestimate me.
Answer:
C
Step-by-step explanation: (look at attachment)
3x + 4 = -2x -2
By looking at the y-intercepts, you automatically know the answer is C.
The y-intercept of the pink line is 4 because of 3x + 4.
The y-intercept of the blue line is -2, because of -2x - 2.
help please without guessing ?//
Answers
Answer:
D. y ≥ x² - 4x - 5
Step-by-step explanation:
We can observe two characteristics of this graphed inequality:
1. its shading is above it, therefore the inequality sign must be greater than
2. its boundary line is continuous, not dotted, so the inequality sign must include or equal to
From these two observations, we can assert that D. x² - 4x - 5 is the correct answer because it is the only one which has a greater than or equal to sign.
____________
Note:
We can also check that the equation for the inequality is correct by converting it to vertex form by completing the square, then graphing it ourselves:
[tex]y \ge (x-2)^2 - 9[/tex]
Answer:
The answer is y≥ x²-4x-5
Step-by-step explanation:
x=a,x=b
where a,b are roots of the equation
a= -1 b=5
x= -1,x=5
x+1=0,x-5=0
(x+1)(x-5)=0
x²-5x+x-5=0
x²-4x-5=0
the anova procedure is a statistical approach for determining whether the means of . a. more than two samples are equal b. two or more populations are equal c. two samples are equal d. two or more samples are equal
Answers
The means of two or more populations being equal is determined by a statistical approach for the ANOVA procedure. Option B is correct.
The ANOVA (Analysis of Variance) procedure is a statistical method used to determine whether there is a significant difference between the means of two or more groups. To statistically test the equality of means ANOVA uses F-tests.
The repeated-measures ANOVA is a two-stage process that is described as an analysis of dependencies. This test is used to prove an assumed cause-effect relationship between variables. The conditions that must be met for the results of an ANOVA are Independence, Random Sampling, Large Sample Size, and Normality.
To learn more about the ANOVA :
https://brainly.com/question/30127764
#SPJ4
justin developed the below hypothesis. h1: younger adults (18-28 years old) spend more time on social media than the middle-aged (29-65 years old) group and older adults (older than 65 years old). what statistical test should he use to test his hypothesis?
Answers
To verify if older adults and middles ages people spend less time on social media, Justin can use the Analysis of variance (ANOVA) test.
ANOVA is used to compare means across two or more groups. Justin can use this test on the different category of younger adults, middle-aged and older adult. This test is done when there is statistically significant difference between the group of samples.
Justin can utilize post-hoc tests (such as Tukey's HSD and Bonferroni) to identify whether particular groups are statistically different from one another if an ANOVA shows a significant difference.
To know more about ANOVA test, visit,
https://brainly.com/question/30127764
#SPJ4
Determine two coterminal angles (one positive and one negative) for each angle. Give your answers in radians. (Enter your answers as a comma-separated list.)
(a)
3/4
Answers
The two coterminal angles for 3/4 radians are (3π + 4)/4 and (-5π + 4)/4 radians.
What is coterminal angles ?Coterminal angles are two or more angles that have the same initial and terminal sides, but differ by a multiple of 360 degrees or 2π radians. In other words, coterminal angles are angles that overlap each other when drawn in standard position (with their initial side on the positive x-axis).
To find two coterminal angles with 3/4 radians, we can add or subtract multiples of 2π radians (which is equivalent to a full circle).
One positive coterminal angle is obtained by adding 2π radians to 3/4 radians:
3/4 + 2π = 3/4 + 8π/4 = 3/4 + 2π
Simplifying, we get:
3/4 + 2π = (3π + 4)/4
Therefore, one positive coterminal angle is (3π + 4)/4 radians.
One negative coterminal angle is obtained by subtracting 2π radians from 3/4 radians:
3/4 - 2π = 3/4 - 8π/4 = 3/4 - 2π
Simplifying, we get:
3/4 - 2π = (-5π + 4)/4
Therefore, one negative coterminal angle is (-5π + 4)/4 radians.
Hence, the two coterminal angles for 3/4 radians are (3π + 4)/4 and (-5π + 4)/4 radians.
To know more about coterminal angles visit:
https://brainly.com/question/23093580
#SPJ1
find the smallest which 108 must be multiplied to get a perfect square
Answers
Answer:
The answer is 3
Step-by-step explanation:
x×108=y
x×2²×3³=y
3×108=324
given: weight a: 140 pounds at 17 inches aft of datum weight b: 120 pounds at 110 inches aft of datum weight c: 85 pounds at 210 inches aft of datum based on this information, the cg would be located how far aft of datum?
Answers
The center of gravity is located 96.7 inches aft of the datum.
To determine the location of the center of gravity (CG) of the system, we need to calculate the moment of each weight about the datum, and then divide the sum of the moments by the total weight of the system.
The moment of each weight is equal to its weight multiplied by its distance from the datum. In this case:
Moment of weight a = 140 pounds x 17 inches = 2,380 inch-pounds
Moment of weight b = 120 pounds x 110 inches = 13,200 inch-pounds
Moment of weight c = 85 pounds x 210 inches = 17,850 inch-pounds
The total weight of the system is:
Total weight = weight a + weight b + weight c = 140 + 120 + 85 = 345 pounds
Therefore, the location of the CG can be calculated as follows:
CG location = (Moment of weight a + Moment of weight b + Moment of weight c) / Total weight
CG location = (2,380 + 13,200 + 17,850) / 345
CG location = 33,430 / 345
CG location = 96.7 inches aft of datum
As a result, the center of gravity is 96.7 inches aft of the datum.
To know more about the Datum, here
https://brainly.com/question/15138411
#SPJ4
HELP MARKING BRAINLEIST
Answers
Answer:
r = 2
center: ( -7,0 )
Step-by-step explanation:
Find the distance, d, of AB.
Answers
The distance between A and B is approximately 8.06 units.
In order to find the distance, d, of AB, we need to use the distance formula. The distance formula gives us the distance between two points in a coordinate plane. It is given as:$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ where (x1, y1) and (x2, y2) are the coordinates of the two points in question.
In this case, A and B are the two points for which we need to find the distance. Let's assume that the coordinates of A are (x1, y1) and the coordinates of B are (x2, y2).
Then the distance formula becomes:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
$$d = \sqrt{((8 + 4) - 2)^2 + ((5 - 1) - 3)^2}$$
$$d = \sqrt{(10 - 2)^2 + (4 - 3)^2}$$
$$d = \sqrt{(8)^2 + (1)^2}$$
$$d = \sqrt{64 + 1}$$
$$d \approx \sqrt{65}$$
$$d \approx 8.06$$
Therefore, the distance between A and B is approximately 8.06 units.
For more such questions on distance, click on:
https://brainly.com/question/26550516
#SPJ8
Alfred buys a car for £13960 which depreciates in value at a rate of 0.75% per year.
Work out how much Alfred's car will be worth in 12 years.
Answers
Answer:
£12063.57
Step-by-step explanation:
The value of Alfred’s car after 12 years can be calculated using the formula for exponential decay: Final Value = Initial Value * (1 - rate of depreciation)^(number of years). Plugging in the values we get: Final Value = 13960 * (1 - 0.0075)^12. Therefore, after 12 years, Alfred’s car will be worth approximately £12063.57.
I don’t know what to write for the equation.
Answers
fraction wise, a whole is always simplified to 1, so
[tex]\cfrac{4}{4}\implies \cfrac{1000}{1000}\implies \cfrac{9999}{9999}\implies \cfrac{17}{17}\implies \text{\LARGE 1} ~~ whole[/tex]
so, we can say the whole of the players, namely all of them, expressed in fourth is well, 4/4, that's the whole lot, and we also know that 3/4 of that is 12, the guys who chose the bottle of water
[tex]\begin{array}{ccll} fraction&value\\ \cline{1-2} \frac{4}{4}&p\\[1em] \frac{3}{4}&12 \end{array}\implies \cfrac{~~ \frac{4 }{4 } ~~}{\frac{3}{4}}~~ = ~~\cfrac{p}{12}\implies \cfrac{~~ 1 ~~}{\frac{3}{4}} = \cfrac{p}{12}\implies \cfrac{4}{3}=\cfrac{p}{12} \\\\\\ (4)(12)=3p\implies \cfrac{(4)(12)}{3}=p\implies 16=p[/tex]
21st term: 3,8,13,18 What is the indicated term
Answers
The 21st term of the sequence 3, 8, 13, 18, .. is 103
To find the indicated term in the sequence, we first need to identify the pattern followed by the sequence. It appears that each term is obtained by adding 5 to the previous term. So, we can write the general formula for the nth term of the arithmetic sequence as
a(n) = a(1) + (n-1)d
where a(1) is the first term of the sequence, d is the common difference, and n is the term number.
In this case, we have:
a(1) = 3 (the first term)
d = 5 (the common difference)
To find the 21st term, we substitute n = 21 in the formula:
a(21) = a(1) + (21-1)d
a(21) = 3 + 20(5)
a(21) = 103
Learn more about arithmetic sequence here
brainly.com/question/16671654
#SPJ4
Using the graph, determine the equation of the axis of symmetry.
Answers
Step-by-step explanation:
x = -4 ( the value of the x-coordinate of the vertex is the axis of symmetry for normal up or down opening parabolas)
Graph Y = 1/2x - 4 on the coordinate plane
Answers
The x-axis and y-axis are two parallel number lines that meet at (0, 0) to form the shape of the letter t.
Describe Coordinate Plane?Geometric objects and mathematical equations are represented on the coordinate plane, a two-dimensional graph. It is made up of the x-axis and y-axis, two parallel number lines that meet at the starting point (0, 0). The horizontal coordinate is represented by the x-axis, while the vertical coordinate is represented by the y-axis. They combine to create the Cartesian coordinate system.
Positive numbers are labelled to the right of the origin and negative values are labelled to the left of the origin on the x-axis. Positive numbers are written above the origin of the y-axis, and negative numbers are written below it. An ordered pair (x, y), where x denotes the horizontal coordinate and y denotes the vertical coordinate, is used to represent each point on the coordinate plane.
For graphing linear equations, quadratic equations, and other functions, the coordinate plane is a helpful tool. Additionally, it is employed to depict geometric forms like polygons, circles, and lines. The distance between two points, the slope of a line, and other significant features of mathematical objects can be calculated by graphing points on the coordinate plane. With applications in physics, engineering, economics, and computer science, the coordinate plane is a fundamental idea in mathematics.
The graph is shown below when y=1.
To know more about graph visit:
brainly.com/question/31090865
#SPJ1
Graph attached below,
The coordinates of the plane is
x y
1 -3.5
2 -3
4 -2
6 -1.
What is equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.
Here the given equation is y = [tex]\frac{1}{2}x-4[/tex].
Now put x= 1 then y = [tex]\frac{1}{2}\times1-4 =\frac{1-8}{2}=\frac{-7}{2}=-3.5[/tex]
Now put x=2 then [tex]y=\frac{1}{2}\times2-4=1-4=-3[/tex]
Now put x=4 then [tex]y=\frac{1}{2}\times4-4=2-4=-2[/tex]
Now put x=6 then [tex]y=\frac{1}{2}\times6-4=3-4=-1[/tex]
Then coordinates of the plane is
x y
1 -3.5
2 -3
4 -2
6 -1.
To learn more about equation refer the below link
https://brainly.com/question/29336774
#SPJ1
102, 107, 99, 102, 111, 95, 91
Mean
Mode
Median
Range
Answers
Answer:
mean: 101 (add all the numbers then divide by 7)
mode: 102 (the most frequent number in the set)
median: 102 (the number in the middle of the set)
range: 20 (the difference between the largest and smallest number)
Mean = 101
Mode = 102
Median = 102
Range = 20
MEAN: Add up all the numbers, then divide by how many numbers there are.
102 + 107 + 99 + 102 + 111 + 95 + 91 = 707
707 ÷ 7 = 101
MODE: Arrange all numbers in order from lowest to highest or highest to lowest and then count how many times each number appears in the set. The one that appears the most is the mode.
91,95,99,102,102,107,111
MEDIAN: Arrange the numbers from smallest to largest. If the amount of numbers is odd, the median is the middle number. If it is even, the median is the average of the two middle numbers in the list.
91,95,99,102,102,107,111
RANGE: Subtract the lowest number from the highest number
111 - 91 = 20
what minus 1 1/2 equals 3 3/4
Answers
Answer:
5 1/4
Step-by-step explanation:
5 × (10 + 7) = (5 × 10) + (5 ×7)
Answers
Answer:
Same equation just using the assocaitive property
Step-by-step explanation:
For example, 8 + (2 + 3) = (8 + 2) + 3 = 13
Hope this helps! =D