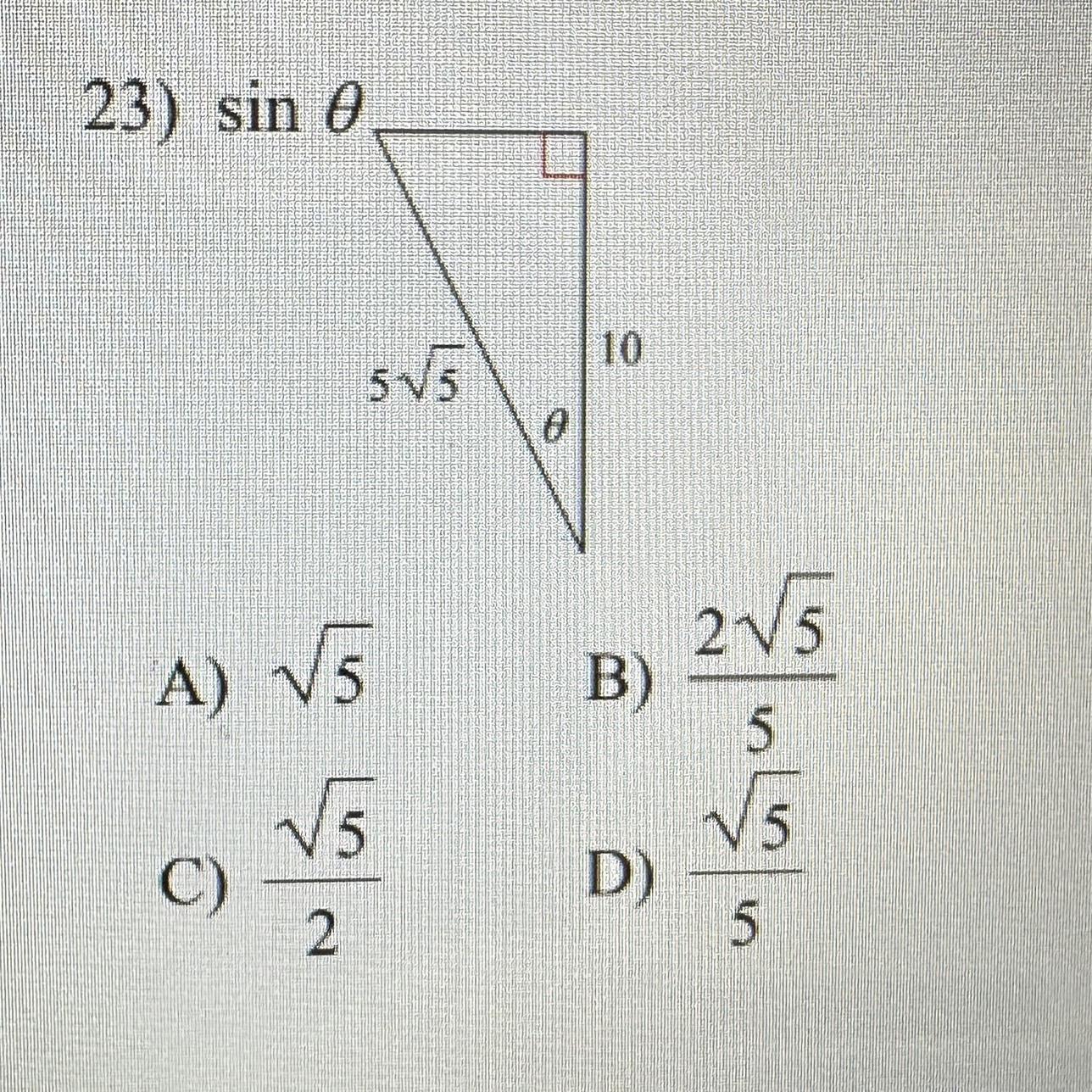Answers
The value of sine θ in the right triangle is (√5)/5.
What is the value of sin(θ)?Using one of the 6 trigonometric ratio:
sine = opposite / hypotenuse
From the figure:
Angle = θ
Adjacent to angle θ = 10
Hypotenuse = 5√5
Opposite = ?
First, we determine the measure of the opposite side to angle θ using the pythagorean theorem:
(Opposite)² = (5√5)² - 10²
(Opposite)² = 125 - 100
(Opposite)² = 25
Opposite = √25
Opposite = 5
Now, we find the value of sin(θ):
sin(θ) = opposite / hypotenuse
sin(θ) = 5/(5√5)
Rationalize the denominator:
sin(θ) = 5/(5√5) × (5√5)/(5√5)
sin(θ) = (25√5)/125
sin(θ) = (√5)/5
Therefore, the value of sin(θ) is (√5)/5.
Option D) (√5)/5 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/3436821
#SPJ1
Related Questions
Below are the summary statistics for the price of televisions ($) at a small electronics store. Lowest price = 250, mean price = 700, median price = 550, range = 1250, IQR=350, Q₁ = 395, standard deviation = 200. Suppose the store increases the price of every television by $20. Tell the new values of each of the summary statistics. New median price = $570 New IQR- $370
Answers
The New median price = $570 and
New IQR = $370
To find the new values of each summary statistic after increasing the price of every television by $20:
New lowest price = $250 + $20 = $270
New mean price = $700 + $20 = $720
New median price remains the same at $570 (since the increase is constant for all prices)
New range = $1250 (since the increase is constant for all prices)
New IQR = $350 (since the increase is constant for all prices)
New Q₁ = $395 + $20 = $415
New standard deviation remains the same at $200 (since the increase is constant for all prices)
Therefore, the new values are:
New median price = $570
New IQR = $370
To know more about statistic, visit:
https://brainly.com/question/30599436
#SPJ11
Ifn=470 and p (p-hat) =0.53, find the margin of error at a 90% confidence level Give your answer to three decimals
Answers
Given that n = 470 and p (p-hat) = 0.53 and we are required to find the margin of error at a 90% confidence level.
First, we find the value of z from the standard normal distribution table that corresponds to a 90% confidence level, which is the complement of the significance level α = 1 - 0.90 = 0.10. Then, we use the formula for the margin of error that involves zα/2, p-hat and q-hat.
As per the formula:
Margin of error = zα/2 [sqrt(p-hat * q-hat)/n]
Here, p-hat = 0.53q-hat = 1 - p-hat = 1 - 0.53 = 0.47
n = 470So,
Margin of error = zα/2 [sqrt(p-hat * q-hat)/n] = z0.05 [sqrt(0.53 * 0.47)/470] = 0.048
We know that at a 90% confidence level, the value of zα/2 is 1.645
Hence, the answer is:
Margin of error = zα/2 [sqrt(p-hat * q-hat)/n] = z0.05 [sqrt(0.53 * 0.47)/470] = 0.048
The margin of error is 0.048, which means that the true population proportion is estimated to be within 0.048 of the sample proportion with 90% confidence. Now, we can construct the confidence interval as:
p-hat ± Margin of error = 0.53 ± 0.048
The lower limit is 0.53 - 0.048 = 0.482
The upper limit is 0.53 + 0.048 = 0.578
Hence, we can conclude that the true population proportion is estimated to be between 0.482 and 0.578 with 90% confidence. Therefore, the conclusion is that the confidence interval for the population proportion at a 90% confidence level is (0.482, 0.578).
To know more about margin of error visit:
brainly.com/question/29419047
#SPJ11
The quality-control manager at a compact fluorescent light bulb (CFL) factory needs to determine whether the mean life of a large shipment of CFLs is equal to 7,495 hours. The population standard deviation is 92 hours. A random sample of 64 light bulbs indicates a sample mean life of 7,472 hours. a. At the 0.05 level of significance, is there evidence that the mean life is different from 7.495 hours? b. Construct a 95% confidence interval estimate of the population mean life of the light bulbs. c. Compare the results of (a) and (c). What conclusions do you reach?
Answers
The null hypothesis is rejected, and the confidence interval does not include 7,495 hours. We conclude that the mean life of the CFLs is different from 7,495 hours.
a. At the 0.05 level of significance, we reject the null hypothesis and conclude that the mean life of the CFLs is different from 7,495 hours.
b. The 95% confidence interval for the population mean life of the light bulbs is 7,429.8 to 7,494.2 hours.
c. The results of (a) and (c) are consistent. The confidence interval does not include 7,495 hours, which supports the conclusion that the mean life of the CFLs is different from 7,495 hours.
Learn more about null hypothesis here:
brainly.com/question/19263925
#SPJ11
Let E be the three-dimensional solid which is in the first octant (x > 0, y ≥ 0 and z≥ 0) and below the plane x+y+z= 3. Set up, but do not evaluate a triple integral for the moment about the xy- plane of an object in the shape of E if the density at the point (x, y, z) is given by the function 8(x, y, z) = xy + 1.
Answers
To set up the triple integral for the moment about the xy-plane of an object in the shape of E, with density given by the function 8(x, y, z) = xy + 1, we need to determine the limits of integration.
The plane x + y + z = 3 intersects the first octant at three points: (3, 0, 0), (0, 3, 0), and (0, 0, 3). These points form a triangle in the xy-plane.
To set up the triple integral, we can express the limits of integration in terms of the variables x and y. The z-coordinate will range from 0 up to the height of the plane at each point in the xy-plane.
For the region in the xy-plane, we can use the limits of integration based on the triangle formed by the points of intersection.
Let's express the limits of integration:
x: 0 to 3 - y - z
y: 0 to 3 - x - z
z: 0 to 3 - x - y
Now, we can set up the triple integral for the moment about the xy-plane:
∫∫∫ (xy + 1) dz dy dx,
with the limits of integration as mentioned above.
To learn more about integration: brainly.com/question/31744185
#SPJ11
Dara Bank conducted a Leveraged buyout of BallbackCo in 2017. The equity contribution at the point of investment was £25 million and the LBO was funded with a term loan of £24 million and senior notes of £6 million. Five years later, Dara are looking to sell the company. The estimated EBITDA for 2022 is £10 million and, following debt repayments, the total debt is now down to £15 million. The exit Enterprise Value relative to EBITDA multiple assumed is 7x. Calculate the IRR and the cash return of the investment.
Answers
After the debt repayments, the total debt is down to £15 million, and the exit Enterprise Value relative to EBITDA multiple assumed is [tex]7x[/tex]. The IRR of the investment is 12.16%, and the cash return is 1.41.
Dara Bank conducted a leveraged buyout of BallbackCo in 2017.
The equity contribution was £25 million, and the LBO was funded with a term loan of £24 million and senior notes of £6 million. Five years later, Dara is looking to sell the company.
The estimated EBITDA for 2022 is £10 million, and after debt repayments, the total debt is now down to £15 million.
The exit Enterprise Value relative to EBITDA multiple assumed is [tex]7x[/tex].
The IRR of the investment is 12.16%, and the cash return is 1.41. Conclusion: Dara Bank conducted an LBO of BallbackCo in 2017, and they are now looking to sell it five years later.
After the debt repayments, the total debt is down to £15 million, and the exit Enterprise Value relative to EBITDA multiple assumed is [tex]7x[/tex]. The IRR of the investment is 12.16%, and the cash return is 1.41.
To know more about Enterprise Value visit:
brainly.com/question/30767816
#SPJ11
Suppose g is a function which has continuous derivatives, and that g(7)=-3, g'(7)=-4, g'(7) = -4,g" (7) = 5. (a) What is the Taylor polynomial of degree 2 for g near 7?
P2(x)=
(b) What is the Taylor polynomial of degree 3 for g near 7?
P3(x)=
(c) Use the two polynomials that you found in parts (a) and (b) to approximate g(6.9).
With P2. g(6.9)
With Ps. 9(6.9)
Answers
The required values are:P2(x) = 5(x - 7)^2/2 - 4(x - 7) - 3P2(6.9)
= 0.015P3(x)
= 7(x - 7)^3/6 - 5(x - 7)^2/2 + 4(x - 7) - 3P3(6.9)
= -2.65.
Given that a function g has continuous derivatives, and g(7)=-3, g'(7)=-4, g'(7) = -4, g" (7) = 5.
(a) We have to find the Taylor polynomial of degree 2 for g near 7.
The Taylor series of a function g, centered at x = a is given by: Pn(x) = f(a) + (x - a)f'(a)/1! + (x - a)^2 f''(a)/2! + ... + (x - a)^n f^n(a)/n!
We have to find the Taylor polynomial of degree 2 for g near 7.
The polynomial of degree 2, P2(x) is given as:P2(x) = g(7) + g'(7)(x-7)/1! + g''(7)(x-7)^2/2!
Now, substituting the values of g(7), g'(7), and g''(7) in the equation of P2(x)P2(x) = -3 + (-4)(x-7) + (5)(x-7)^2/2P2(x)
= 5(x - 7)^2/2 - 4(x - 7) - 3
(b) We have to find the Taylor polynomial of degree 3 for g near 7.
The polynomial of degree 3, P3(x) is given as:
P3(x) = g(7) + g'(7)(x-7)/1! + g''(7)(x-7)^2/2! + g'''(7)(x-7)^3/3!
Now, substituting the values of g(7), g'(7), g''(7), and g'''(7) in the equation of P3(x), we get
P3(x) = -3 + (-4)(x-7) + (5)(x-7)^2/2 - (7/3)(x-7)^3P3(x)
= 7(x - 7)^3/6 - 5(x - 7)^2/2 + 4(x - 7) - 3(c)
We have to use the two polynomials found in (a) and (b) to approximate g(6.9).
With P2: We know that
P2(x) = 5(x - 7)^2/2 - 4(x - 7) - 3
Thus,
P2(6.9) = 5(6.9 - 7)^2/2 - 4(6.9 - 7) - 3
= 0.015 (approx)
With P3: We know that P3(x) = 7(x - 7)^3/6 - 5(x - 7)^2/2 + 4(x - 7) - 3
Thus, P3(6.9) = 7(6.9 - 7)^3/6 - 5(6.9 - 7)^2/2 + 4(6.9 - 7) - 3
= -2.65 (approx)
Hence, the required values are:P2(x) = 5(x - 7)^2/2 - 4(x - 7) - 3P2(6.9)
= 0.015P3(x)
= 7(x - 7)^3/6 - 5(x - 7)^2/2 + 4(x - 7) - 3P3(6.9)
= -2.65.
To learn more about function visit;
https://brainly.com/question/30721594
#SPJ11
determine whether the geometric series is convergent or divergent. 10 − 2 + 0.4 − 0.08 +
Answers
Answer:
This geometric series is convergent:
[tex] \frac{10}{1 - ( - \frac{1}{5}) } = \frac{10}{ \frac{6}{5} } = 10( \frac{5}{6} ) = \frac{25}{3} = 8 \frac{1}{3} [/tex]
The geometric series 10 - 2 + 0.4 - 0.08 + ... is convergent.
To determine if the geometric series 10 - 2 + 0.4 - 0.08 + ... is convergent or divergent, we need to examine the common ratio (r) between consecutive terms.
The common ratio (r) can be found by dividing any term by its preceding term.
Let's calculate it:
r = (-2) ÷ 10 = -0.2
r = 0.4 ÷ (-2) = -0.2
r = (-0.08) ÷ 0.4 = -0.2
In this series, the common ratio (r) is -0.2.
For a geometric series to be convergent, the absolute value of the common ratio (|r|) must be less than 1. If |r| ≥ 1, the series is divergent.
In this case, |r| = |-0.2| = 0.2 < 1.
Since the absolute value of the common ratio is less than 1, the geometric series 10 - 2 + 0.4 - 0.08 + ... is convergent.
To know more about Geometric Series:
https://brainly.com/question/11873791
Recall that for a permutation f of [n], an r-cycle of f is r distinct elements of [n] that are cyclically permuted by f. Compute the number of permutations of [n] with no r-cycles for each n and r. Hint: The case r = 1 gives the derangement number Dn.
use Inclusion_Exclusion
Answers
we obtain the number of permutations of [n] with no r-cycles as: P(n, r) = (n! / r!) - (n choose r) * (n-1)! + ((n choose r) choose 2) * (n-2)!
The number of permutations of [n] with no r-cycles can be computed using the principle of inclusion-exclusion. Let's denote the number of such permutations as P(n, r).
To calculate P(n, r), we start by considering all permutations of [n], which is n!. However, this includes permutations with r-cycles. We want to exclude these permutations.
First, let's consider permutations with a single r-cycle. There are (n-1)! ways to bthe remaining (n-r) elements while fixing the positions of the r elements in the cycle. We can choose the r elements for the cycle in (n choose r) ways. Therefore, the number of permutations with a single r-cycle is (n choose r) * (n-1)!.
However, this excludes permutations with multiple r-cycles. To include permutations with two r-cycles, we need to subtract the count of these permutations. There are (n-2)! ways to arrange the remaining (n-2r) elements while fixing the positions of the 2r elements in the cycles. We can choose the 2r elements for the cycles in ((n choose r) choose 2) ways. Therefore, the number of permutations with two r-cycles is ((n choose r) choose 2) * (n-2)!.
We continue this process for each possible number of r-cycles, alternating between addition and subtraction. Finally, we obtain the number of permutations of [n] with no r-cycles as:
P(n, r) = (n! / r!) - (n choose r) * (n-1)! + ((n choose r) choose 2) * (n-2)! - ...
This formula accounts for all possible combinations of r-cycles and gives us the desired result.
To know more about permutations , refer here:
https://brainly.com/question/32683496#
#SPJ11
for the given parametric equations, find the points (x, y) corresponding to the parameter values t = −2, −1, 0, 1, 2. x = 5t2 5t, y = 3t 1
Answers
The points corresponding to the parameter values are: (-2, -7), (-1, -4), (0, -1), (1, 2), (2, 5).To find the points (x, y) corresponding to the parameter values t = -2, -1, 0, 1, 2, we substitute these values of 't' into the given parametric equations:
For t = -2: x = [tex]5(-2)^2[/tex] + 5(-2) = 20 - 10 = 10
y = 3(-2) - 1 = -6 - 1 = -7
So the point is (10, -7).
For t = -1: x = [tex]5(-1)^2[/tex] + 5(-1) = 5 - 5 = 0,y = 3(-1) - 1 = -3 - 1 = -4
So the point is (0, -4).
For t = 0: x =[tex]5(0)^2[/tex]+ 5(0) = 0 + 0 = 0, y = 3(0) - 1 = 0 - 1 = -1
So the point is (0, -1).
For t = 1: x = [tex]5(1)^2[/tex] + 5(1) = 5 + 5 = 10, y = 3(1) - 1 = 3 - 1 = 2
So the point is (10, 2).
For t = 2: x = [tex]5(2)^2[/tex]+ 5(2) = 20 + 10 = 30,y = 3(2) - 1 = 6 - 1 = 5
So the point is (30, 5).
Therefore, the points corresponding to the parameter values are:
(-2, -7), (-1, -4), (0, -1), (1, 2), (2, 5).
To know more about Parametric equations visit-
brainly.com/question/30748687
#SPJ11
The number of welfare cases in a city of population p is expected to be 0.00%) the population is growing by 900 people per year, find the rate at which the number of welfare cases will be increasing when the population is p= 1,000,000. ______ cases per yr
Answers
When the population of the city is 1,000,000 and growing at a rate of 900 people per year, the number of welfare cases is expected to increase by approximately 3,690 cases per year.
To find the rate at which the number of welfare cases will be increasing, we need to consider the growth rate of the population and the percentage of welfare cases.
Given that the expected number of welfare cases is 0.00% of the population, we can assume that the number of welfare cases is directly proportional to the population.
Let's denote the number of welfare cases as C and the population as P. We can express the relationship as C = k .P, where k is a constant. Since the expected number of welfare cases is 0.00%, we can substitute C = 0.00% of P, or C = 0.0000. P.
Now, we can calculate the derivative of C with respect to time t to find the rate of change:
dC/dt = d/dt (0.0000. P)
Since P is growing at a rate of 900 people per year, we can express it as dP/dt = 900. Substituting this into the derivative equation:
dC/dt = d/dt (0.0000. P)
= 0.0000. dP/dt
= 0.0000. 900
= 0
Therefore, the rate at which the number of welfare cases is increasing when the population is 1,000,000 and growing at a rate of 900 people per year is 0 cases per year. This means that the number of welfare cases remains constant, assuming the expected percentage of 0.00% holds true.
Learn more about growth rate here:
https://brainly.com/question/7414993
#SPJ11
Find the value of the following:
a. t0.05,9
b. t0.025,11
C. X^2 0.10,2
d. X^2 0.01,4
Answers
To find the values of t and chi-square critical values, we need to refer to the t-distribution and chi-square distribution tables. The values are typically used for hypothesis testing or constructing confidence intervals. For the given options, the values are as follows:
a. t0.05,9 ≈ 1.833
b. t0.025,11 ≈ 2.718
c. X^2 0.10,2 ≈ 4.605
d. X^2 0.01,4 ≈ 13.277
a. To find t0.05,9, we refer to the t-distribution table with 9 degrees of freedom and a significance level of 0.05. The value is approximately 1.833. b. For t0.025,11, we consult the t-distribution table with 11 degrees of freedom and a significance level of 0.025. The value is approximately 2.718.
c. To determine X^2 0.10,2, we refer to the chi-square distribution table with 2 degrees of freedom and a significance level of 0.10. The value is approximately 4.605. d. For X^2 0.01,4, we consult the chi-square distribution table with 4 degrees of freedom and a significance level of 0.01. The value is approximately 13.277.
These values are important in statistical analysis for conducting hypothesis tests, calculating confidence intervals, or making decisions based on specific significance levels. They provide critical values that help determine the acceptance or rejection of hypotheses and the construction of confidence intervals for various statistical tests and analyses.
Learn more about statistics here: brainly.com/question/32201536
#SPJ11
(12t-12,cos(3mt)-12mt,3t²) is Find the value of t for which the tangent line to the curve r(t)= perpendicular to the plane 3x-3πу+30z=-5. (Type your answer is an integer, digits only, no letters, no plus or minus. Hint. The tangent vector to the curve should be proportional to the normal vector to the plane.)
Answers
To find value of t for which the tangent line to curve r(t) = (12t-12, cos(3mt)-12mt, 3t²) is perpendicular to plane 3x-3πy+30z=-5, we to tangent vector to curve is proportional to the normal vector of the plane.
The tangent vector to the curve r(t) is given by the derivative of r(t) with respect to t. Taking the derivative, we find r'(t) = (12, -3m sin(3mt)-12m, 6t).
The normal vector to the plane 3x-3πy+30z=-5 is (3, -3π, 30).For the tangent line to be perpendicular to the plane, the dot product of the tangent vector and the normal vector should be zero. Calculating the dot product, we have:
(12, -3m sin(3mt)-12m, 6t) · (3, -3π, 30) = 12(3) + (-3m sin(3mt)-12m)(-3π) + 6t(30) = 36 + 9πm sin(3mt) + 36m - 180t = 0.
Now, we need to solve this equation to find the value of t. This may involve using numerical methods or further simplification depending on the given value of m.Once the equation is solved, we will obtain the value of t, which corresponds to the point on the curve where the tangent line is perpendicular to the given plane.
To learn more about tangent line click here :
brainly.com/question/23416900
#SPJ11
complete and balance the following half-reaction: cr(oh)3(s)→cro2−4(aq) (basic solution)
Answers
The completed and balanced half-reaction in basic solution is, cr(oh)3(s) + 4OH− (aq) → cro2−4(aq) + 3H2O (l).
The half-reaction that is completed and balanced in basic solution for the reaction, cr(oh)3(s) → cro2−4(aq) is as follows:
Firstly, balance all of the atoms except H and OCr(OH)3 (s) → CrO42− (aq)
Now, add water to balance oxygen atoms
Cr(OH)3 (s) → CrO42− (aq) + 2H2O (l)
Then, balance the charge by adding OH− ionsCr(OH)3 (s) + 4OH− (aq) → CrO42− (aq) + 3H2O (l)
Thus, the completed and balanced half-reaction in basic solution is, cr(oh)3(s) + 4OH− (aq) → cro2−4(aq) + 3H2O (l).
Learn more about chemical reaction at:
https://brainly.com/question/29321325
#SPJ11
The general solution of (D²-2D+1)y=2sin x
A. y=c₁ex+c₂xex + sinx+cos x
B. y=c₁ex+c₂xe* + sinx
C. y=c₁ex+c₂xex + 2 sinx
D. y=C1eX +C2XeX+cosx
Answers
The general solution is Option (A).
Given equation is (D²-2D+1)y=2sin x
We know that, D²-2D+1=(D-1)²
So, the equation becomes (D-1)²y = 2sinx
Since (D-1)² = D² - 2D +1 is a second-order homogeneous differential equation with constant coefficients with the characteristic equation r²-2r+1=0
The roots of the equation are r=1
The general solution of the differential equation
(D²-2D+1)y=2sin x
is given by the equation
y = (c₁ + c₂x)e^x + sin(x)
Where c₁ and c₂ are constants.
Hence the correct option is (A) y=c₁ex+c₂xex + sinx+cosx.
#SPJ11
Let us know more about general solution : https://brainly.com/question/32062078.
The owner of a fish market has an assistant who has determined that the weights of catfish are normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound. If a sample of 64 fish yields a mean of 3.4 pounds, what is probability of obtaining a sample mean this large or larger?
a. 0.0001
b. 0.0228
c. 0.0013
d. 0.4987
Answers
The probability of obtaining a sample mean as large or larger is 0.0228.
option B.
What is the probability of obtaining a sample mean this large or larger?The probability of obtaining a sample mean as large or larger is calculated as follows;
The given parameters;
Population mean (μ) = 3.2 poundsPopulation standard deviation (σ) = 0.8 poundSample size (n) = 64Sample mean (x) = 3.4 poundsThe standard error (SE) of the sampling distribution is calculated as;
SE = σ / √n
SE = 0.8 / √64
SE = 0.8 / 8
SE = 0.1
The z-score of the sample mean is calculated as follows;
z = (x - μ) / SE
z = (3.4 - 3.2) / 0.1
z = 0.2 / 0.1
z = 2
Using a z-score calculator;
P (X > Z) = 0.0228
Learn more about z-score here: https://brainly.com/question/25638875
#SPJ4
The probability of obtaining a sample mean as large or larger than 3.4 pounds is 0.0228.
The correct answer is: b. 0.0228
What is the probability?Given data:
Population mean (μ) = 3.2 pounds
Population standard deviation (σ) = 0.8 pound
Sample size (n) = 64
Sample mean (x) = 3.4 pounds
We have to standardize the sample mean using the z-score formula and then find the corresponding area under the standard normal distribution curve.
The formula for calculating the z-score is:
z = (x - μ) / (σ / √n)
substituting the values:
z = (3.4 - 3.2) / (0.8 / √64)
z = 0.2 / (0.8 / 8)
z = 0.2 / 0.1
z = 2
Using a calculator, the area to the right of z = 2 is the probability 0.0228.
Learn more about probability at:
#SPJ4
Find the power series representation for where en =
f(x) = ∫x-0 tan⁻¹t / dt f(x) = ∑[infinity] n=1 (-1)ˆen anxpn A. n
B. n-1
C. 0
Answers
To find the power series representation for the function f(x) = ∫₀ˣ tan⁻¹(t) dt, we can use the Maclaurin series expansion for the arctan function.
The Maclaurin series expansion for arctan(t) is:
arctan(t) = t - (t³/3) + (t⁵/5) - (t⁷/7) + ...
To find the power series representation for f(x), we integrate the Maclaurin series term by term:
∫₀ˣ arctan(t) dt = ∫₀ˣ (t - (t³/3) + (t⁵/5) - (t⁷/7) + ...) dt
We can integrate each term of the series separately:
∫₀ˣ t dt = (1/2)t² + C₁
∫₀ˣ (t³/3) dt = (1/12)t⁴ + C₂
∫₀ˣ (t⁵/5) dt = (1/60)t⁶ + C₃
∫₀ˣ (t⁷/7) dt = (1/420)t⁸ + C₄
...
Combining the results, we have:
f(x) = (1/2)t² - (1/12)t⁴ + (1/60)t⁶ - (1/420)t⁸ + ...
Since we are integrating from 0 to x, we replace t with x in the series:
f(x) = (1/2)x² - (1/12)x⁴ + (1/60)x⁶ - (1/420)x⁸ + ...
Therefore, the power series representation for f(x) is:
f(x) = ∑[infinity] n=1 (-1)^(n+1) (1/(2n-1))x^(2n)
In this representation, each term has a coefficient of (-1)^(n+1) and a power of x raised to (2n). The series converges for all values of x within the interval of convergence.
To learn more about coefficient : brainly.com/question/1594145
#SPJ11
What is the rationale behind the polynomial and the power
methods for determining eigenvalues?
What are their strengths and limitations?
Answers
The polynomial and power methods are numerical techniques used to determine the eigenvalues of a matrix.
The polynomial method is based on the fact that if a matrix A has an eigenvalue λ, then the determinant of the matrix (A - λI) is zero, where I is the identity matrix. This leads to a polynomial equation of degree n (where n is the size of the matrix) that can be solved to find the eigenvalues. The power method, on the other hand, utilizes the dominant eigenvalue and its corresponding eigenvector. It starts with an initial guess for the dominant eigenvector and iteratively multiplies it by matrix A, normalizing it at each step. This process converges to the dominant eigenvector, and the corresponding eigenvalue can be obtained by the Rayleigh quotient.
The strengths of the polynomial method include its ability to find all eigenvalues of a matrix and its simplicity in implementation. However, it can be computationally expensive for large matrices and is sensitive to ill-conditioned matrices. The power method is efficient for finding the dominant eigenvalue and corresponding eigenvector of a matrix. It converges quickly for matrices with a clear dominant eigenvalue. However, it may fail to converge for matrices without a dominant eigenvalue or when multiple eigenvalues have similar magnitudes.
The polynomial method is suitable for finding all eigenvalues, while the power method is effective for determining the dominant eigenvalue. Both methods have their strengths and limitations, and the choice of method depends on the specific characteristics of the matrix and the desired eigenvalue information.
Learn more about polynomials here: brainly.com/question/54172210
#SPJ11
the length of the curve y = sin(3x) from x = 0 to x=π6 is given by
Answers
The length of the curve y = sin(3x)
from x = 0
to x = π/6 is given by
[tex]\frac{1}{3}(\sqrt {10} + 3\ln (2 + \sqrt 3 ))[/tex]
The length of the curve y = sin(3x)
from x = 0
to x = π/6 is given by:
[tex]$\int\limits_0^{\pi/6} {\sqrt {1 + {({y^{'}})^2}} dx}$[/tex]
Given, the curve is y = sin(3x)
We have to find the length of the curve from x = 0
to x = π/6 using the formula
[tex]$\int\limits_0^{\pi/6} {\sqrt {1 + {({y^{'}})^2}} dx}$[/tex]
We know that the derivative of y with respect to x is y',
so y' = 3cos(3x)
Using the formula we get,
[tex]$\int\limits_0^{\pi/6} {\sqrt {1 + {({y^{'}})^2}} dx}[/tex]
=[tex]\int\limits_0^{\pi/6} {\sqrt {1 + 9{{\cos }^2}3x} dx} $[/tex]
Now, substitute u = 3x,
then [tex]$\frac{du}{dx} = 3$[/tex]
and [tex]$dx = \frac{1}{3}du$[/tex]
Hence, the integral becomes
[tex]$\int\limits_0^{\pi/6} {\sqrt {1 + 9{{\cos }^2}3x} dx}[/tex]
= [tex]\frac{1}{3}\int\limits_0^{\pi/2} {\sqrt {1 + 9{{\cos }^2}u} du}[/tex]
Let's substitute [tex]$t = \tan u$[/tex],
then dt =[tex]{\sec ^2}udu$ and $\sec^2 u[/tex]
=1 + \tan^2 u
=[tex]1 + {t^2}$[/tex]
Also, when $u = 0,
t =[tex]\tan 0[/tex]
= 0
and when [tex]$u = \frac{\pi}{6},[/tex]
t =[tex]\tan \frac{\pi}{6}[/tex]
= [tex]\frac{\sqrt 3 }{3}$[/tex]
Hence, the integral becomes
[tex]$\frac{1}{3}\int\limits_0^{\pi/2} {\sqrt {1 + 9{{\cos }^2}u} du}[/tex]
=[tex]\frac{1}{3}\int\limits_0^{\sqrt 3 /3} {\sqrt {1 + {{\sec }^2}{\tan ^{ - 1}}t} dt} \\[/tex]
=[tex]\frac{1}{3}\int\limits_0^{\sqrt 3 /3} {\sqrt {1 + {{(1 + {t^2})}^2}} dt} \frac{1}{3}\int\limits_0^{\sqrt 3 /3} {\sqrt {1 + {{(1 + {t^2})}^2}} dt}[/tex]
On simplifying and solving the integral, we get the length of the curve from x = 0
to x = π/6 is given by
[tex]L = \frac{1}{3}(\sqrt {10} + 3\ln (2 + \sqrt 3 ))[/tex]
Therefore, the length of the curve y = sin(3x) from x = 0 to x = π/6 is given by [tex]$\frac{1}{3}(\sqrt {10} + 3\ln (2 + \sqrt 3 ))$[/tex]
To know more about integral visit:
https://brainly.com/question/30094386
#SPJ11
Question 11 (17,0 marks) The random variables X and Y have the joint PDF for some constant c. 11.1 (5.0 marks) ا 17 Previous 123456 7 8 9 10 11 12 Next Validate Mark Unfocus Help ifx+ys1, x20, y20 fx
Answers
Question 11 discusses the joint PDF of X and Y, with conditions on their ranges and an expression involving their relationship.
What is the content of question 11 regarding the joint probability density function of random variables X and Y?
The paragraph mentions question 11, which involves random variables X and Y with a joint probability density function (PDF) represented by a constant c.
It further mentions the conditions for the variables, such as x ranging from 0 to 20 and y ranging from 0 to 20.
The expression "fx+ys1" suggests a mathematical relationship between X and Y, but the specific details and context are not provided.
The paragraph also refers to the need to validate and mark the question, indicating an evaluation or assessment process.
However, without further information or context, it is difficult to provide a detailed explanation of the paragraph's content.
Learn more about Question 11
brainly.com/question/16882326
#SPJ11
solce each equation for 0 ≤ θ< 360. Round to nearest hundredth
13) 1-tan θ = -17.6
Answers
To solve the equation, we will add tan θ on both sides:1 - tan θ + tan θ = -17.6 + tan θ0.375 tanθ = -17.6
Then, we will divide both sides by 0.375tanθ = -17.6/0.375= -46.93
Using the inverse tangent function, we can find θθ = tan⁻¹(-46.93)θ = -88.21Explanation:We have solved the equation using the formula derived from trigonometric ratios.
After rearranging the equation and adding tanθ to both sides, we were left with 0.375 tanθ = -17.6. We then divided the equation by 0.375 and found that tanθ = -46.93.
Using the inverse tangent function, we can find θ. The resulting value is -88.21.
Summary:To solve the equation 1 - tan θ = -17.6, we added tan θ to both sides and derived the formula from trigonometric ratios. After rearranging the equation, we found the value of tanθ and then used the inverse tangent function to find the value of θ. The final value of θ was found to be -88.21.
Learn more about equation click here:
https://brainly.com/question/2972832
#SPJ11
You draw a card from a standard deck of cards, put it back, and then draw another card. What is the probability of drawing a diamond and then a black card
Answers
Step-by-step explanation:
There are 52 cards 13 are diamonds 26 are black
13 out of 52 times 26 out of 52 =
13/52 X 26/52 = 1/8 = .125
The distance of a single score from the mean - for example, the distance of your exam score from the average exam score for the entire class - is referred to as what? Variance Deviation Sum of Squared
Answers
Deviation is referred to as the distance of a single score from the mean - for example, the distance of your exam score from the average exam score for the entire class
The distance of a single score from the mean - for example, the distance of your exam score from the average exam score for the entire class - is referred to as Deviation.
:In statistics, deviation refers to the amount by which a single observation or an entire dataset varies or differs from the given data's average value, such as the mean.
This definition encompasses the concept of deviation in both descriptive and inferential statistics. Deviation is usually measured by standard deviation or variance. A deviation is a measure of how far away from the central tendency an individual data point is.
Summary: Deviation is referred to as the distance of a single score from the mean - for example, the distance of your exam score from the average exam score for the entire class. The formula for deviation is given by: Deviation = Observation value - Mean value of the given data set.
Learn more about mean click here:
https://brainly.com/question/1136789
#SPJ11
Consider the following two subsets of Z :
A = { n Î Z | ( n mod 18 ) = 7 } and B = { n Î Z | n is
odd }.
Prove this claim: A is a subset of B.
Answers
To prove that A is a subset of B, we need to show that every element in A is also an element of B. A is an arbitrary element .
Let's consider an arbitrary element n in A, where (n mod 18) = 7. Since n satisfies this condition, it means that n leaves a remainder of 7 when divided by 18.
Now, we need to show that n is also an odd number. An odd number is defined as an integer that is not divisible by 2.
Since n leaves a remainder of 7 when divided by 18, it implies that n is not divisible by 2. Hence, n is an odd number.
Therefore, we have shown that for any arbitrary element n in A, it is also an element of B. Hence, A is a subset of B.
To learn more about Integer - brainly.com/question/1768254
#SPJ11
Determine interior, accumulation and isolated points for the following sets (A= (-4,15]\{10} (3 marks) (ii) B = (0,1) nQ, where Q is set of rational numbers. (3 marks) I Borgeren W P e
Answers
Interior points: The point x ∈ S is known as an interior point of S if there exists a neighborhood of x that is completely contained in S. Given, A= (-4,15] \ {10} and B = (0,1) ∩ Q, where Q is a set of rational numbers.
We need to determine the interior, accumulation, and isolated points for the given sets. So, A= (-4,15] \ {10}. Here, the point is not included so, the interior point of set A is all points within the interval (-4, 10) and (10, 15]. It can also be written asInt A = (-4,10) U (10,15] Accumulation Points: Let S be a set of real numbers and x ∈ R be a limit point of S if every ε-neighborhood of x intersects S in a point other than x. So, A= (-4,15] \ {10}. Hence the limit points of A are -4, 10, and 15. Isolated points: A point x ∈ S is known as an isolated point of S if x is not a limit point of S. Here, the point x=10 ∈ A is an isolated point of A. B = (0,1) ∩ Q, where Q is a set of rational numbers Interior points: Since Q is dense in R, every point of (0,1) is an accumulation point of Q. Thus there are no interior points in B, i.e., int B = ∅. Accumulation Points: Since Q is dense in R, every point of (0,1) is an accumulation point of Q. Therefore, all points of (0,1) are the accumulation points of B. Isolated points: The isolated points of the set B are all points of (0,1) that are not rational numbers. That is, the isolated points of the set B are all irrational numbers in (0,1).
The given sets A= (-4,15] \ {10} and B = (0,1) ∩ Q, where Q is a set of rational numbers that are examined for interior points, accumulation points, and isolated points. For set A, the interior points are (-4,10) U (10,15], the limit points are -4, 10, and 15, and the isolated point is 10. For set B, there are no interior points, all points of (0,1) are accumulation points, and the isolated points are irrational numbers in (0,1).
To know more about interior point visit;
brainly.com/question/28598514
#SPJ11
Select the cost of the best alternative. MARR=10% per year. Use 2 decimal places after dot for the values you take from interest rate table.
A
B
Initial Cost, $
-25000
-32000
Annual Cost, $/year
-9000
-7000
Annual Revenue, $/year
3200
1900
Deposit Return, $
5000
9000
n, years
4
Select one:
O a. 40047
Ob. 41986
O c. 39986
Od. 42047
Oe. 35691
Answers
To select the cost of the best alternative, we need to calculate the Present Worth (PW) of each alternative and choose the one with the lowest PW. The Minimum Acceptable Rate of Return (MARR) is given as 10% per year.
Let's calculate the PW for each alternative:
Alternative A:
Initial Cost: -$25,000
Annual Cost: -$9,000
Annual Revenue: $3,200
Deposit Return: $5,000
n: 4 years
The PW of Alternative A can be calculated as follows:
[tex]PW(A) = \text{Initial Cost} + \text{Annual Cost}(P/A, 10\%, 4) + \text{Annual Revenue}(P/G, 10\%, 4) + \text{Deposit Return}(P/F, 10\%, 4)\\\\= -25000 + (-9000)(P/A, 10\%, 4) + (3200)(P/G, 10\%, 4) + (5000)(P/F, 10\%, 4)[/tex]
Using the interest rate table, we can find the factors:
[tex]P/A, 10\%, 4 = 3.16986 \\P/G, 10\%, 4 = 3.16986 \\P/F, 10\%, 4 = 0.68301 \\[/tex]
Substituting these values into the equation:
[tex]PW(A) = -25000 + (-9000)(3.16986) + (3200)(3.16986) + (5000)(0.68301) \\= -25000 - 28529.74 + 10156.99 + 3415.05 \\= -\$39957.70[/tex]
Alternative B:
Initial Cost: -$32,000
Annual Cost: -$7,000
Annual Revenue: $1,900
Deposit Return: $9,000
n: 4 years
Using the same approach, we can calculate the PW of Alternative B:
[tex]PW(B) = -32000 + (-7000)(P/A, 10\%, 4) + (1900)(P/G, 10\%, 4) + (9000)(P/F, 10\%, 4)[/tex]
Using the interest rate table:
[tex]P/A, 10\%, 4 = 3.16986 \\P/G, 10\%, 4 = 3.16986 \\P/F, 10\%, 4 = 0.68301 \\[/tex]
Substituting the values:
[tex]PW(B) = -32000 + (-7000)(3.16986) + (1900)(3.16986) + (9000)(0.68301) \\= -32000 - 22189.02 + 6010.74 + 6147.09 \\= -\$42031.19[/tex]
Comparing the PWs of the two alternatives, we see that PW(A) is -$39957.70 and PW(B) is -$42031.19. Since PW(A) has a lower value, the cost of the best alternative is -$39957.70.
Therefore, the correct answer is:
c. 39986
To know more about Value visit-
brainly.com/question/30760879
#SPJ11
let g be the function with first derivative g′(x)=x3 x−−−−−√ for x>0. if g(2)=−7, what is the value of g(5) ?
Answers
First derivative of the function g′(x)=x³/√x for x > 0
The value of g(5) is 250/3√5 - 23/3.
Let's find the solution to the given question.
We have, First derivative of the function g′(x)=x³/√x for x > 0
Integrating the first derivative to get the function, we have
∫g′(x) dx=∫x³/√x dx=∫x²√x dx
=x²(2/3)x³/2/3 + C
=2/3[tex]x^{5/2}[/tex] + C where
C is a constant of integration,
which we get from the boundary condition g(2) = -7.
So, g(2) = -7
=>2²(2/3) + C = -7
=> C = -23/3
Therefore, g(x) = 2/3[tex]x^{5/2}[/tex] - 23/3
Therefore, g(5) = [tex]2/3(5)^{(5/2)}[/tex]- 23/3
=[tex]2/3(5\times5\times5^{(1/2)})[/tex] - 23/3
=2 × 125/3×√5 - 23/3
= 250/3√5 - 23/3
Therefore, the value of g(5) is 250/3√5 - 23/3.
To know more about constant of integration, visit:
https://brainly.com/question/29166386
#SPJ11
4) Find the sum of the series: -3 +21 + -147+1029... +121060821=
Answers
The sum of the series is -63.75.
We have,
To find the sum of the given series, we notice that each term alternates between a negative and positive value.
The series seems to follow a pattern of multiplying each term by -7. Let's verify this pattern and find the sum.
Starting with the first term:
-3
The second term is obtained by multiplying the previous term by -7:
-3 * -7 = 21
The third term is obtained by multiplying the second term by -7:
21 * -7 = -147
We can observe that each term is obtained by multiplying the previous term by -7.
Therefore, the pattern holds.
Now, let's find the sum of the series.
We can use the formula for the sum of a geometric series:
Sum = (first term) x (1 - (common ratio)^(number of terms)) / (1 - (common ratio))
In this case,
The first term is -3 and the common ratio is -7.
We need to determine the number of terms.
To find the number of terms, we need to find the exponent to which -7 is raised to obtain the last term, which is 121060821. Let's calculate this exponent:
-3 x (-7)^(n-1) = 121060821
Divide both sides by -3:
(-7)^(n-1) = -40353607
Since -7 raised to an odd power is negative and -40353607 is negative, we know that n - 1 must be an even number.
Let's find the smallest even exponent that gives a negative result:
(-7)^2 = 49
(-7)^4 = 2401
(-7)^6 = 117649
(-7)^8 = 5764801
(-7)^10 = 282475249
(-7)^12 = 13841287201
We can see that (-7)^12 is the smallest even exponent that gives a negative result. Therefore, n-1 must be 12, so n = 13.
Now, let's substitute the values into the formula to find the sum:
Sum = (-3) x (1 - (-7)^13) / (1 - (-7))
= (-3) x (1 - (-169)) / (1 + 7)
= (-3) x (1 + 169) / 8
= (-3) x 170 / 8
= -510 / 8
= -63.75
Therefore,
The sum of the series is -63.75.
Learn more about the series here:
https://brainly.com/question/30457228
#SPJ1
Get a similar question You can retry this question below The average THC content of marijuana sold on the street is 9.8%. Suppose the THC content is normally distributed with standard deviation of 2%. Let X be the THC content for a randomly selected bag of marijuana that is sold on the street. Round all answers to 4 decimal places where possible, a. What is the distribution of X? X - NO b. Find the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 9.1. c. Find the 64th percentile for this distribution. % Hint: Helpful videos: • Find a Probability [+] 7 Finding a Value Given a Probability [+] Hint Submit
Answers
The distribution of X is normally distributed.
The given information states that the THC content of marijuana sold on the street is normally distributed with a mean of 9.8% and a standard deviation of 2%. This means that the THC content follows a bell-shaped curve, where the majority of values will be around the mean of 9.8%.
In statistical terms, we can represent the THC content as a random variable X. Since X is normally distributed, we can use the notation X ~ N(9.8, 0.02^2), where N represents the normal distribution, 9.8 is the mean, and 0.02 is the standard deviation.
To find the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 9.1, we need to calculate the area under the curve to the right of 9.1. This can be done by finding the z-score corresponding to 9.1, which measures the number of standard deviations a value is away from the mean. Using the formula z = (X - μ) / σ, we can calculate the z-score as (9.1 - 9.8) / 0.02 = -3.5.
Now, we can use a standard normal distribution table or a calculator to find the probability associated with a z-score of -3.5. The probability corresponds to the area under the curve to the right of the z-score. In this case, the probability is approximately 0.0002327, rounded to 4 decimal places. Therefore, the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 9.1 is approximately 0.0002.
Learn more about normal distribution
brainly.com/question/15103234
#SPJ11
TRUE OR FALSE ANOVA tests use which of the following distributions? Z F t chi-square 8 2 points The alternative hypothesis for ANOVA is that all populations means are different. True False 2 points Five new medicines (FluGone, SneezAb, Medic, RecFlu, and Fevir) were studied for treating the flu. 25 flu patients were randomly assigned into one of the five groups and received the assigned medication. Their recovery times from the flu were recorded. How many degrees of freedom for treatment are there? Type your answer..... 0000
Answers
It is true that ANOVA tests use F distributions. ANOVA tests use F distributions. It is a statistical technique used to evaluate the differences between two or more means.
The null hypothesis in ANOVA is that all population means are equal, and the alternative hypothesis is that at least one population mean is different.
Therefore, the alternative hypothesis for ANOVA is that all populations mean are different.
The total degrees of freedom are n – 1
= 25 – 1
= 24.
The degrees of freedom for treatment are k - 1, where k is the number of groups or treatments. In this case, there are 5 groups or treatments,
so the degrees of freedom for treatment are 5 - 1
= 4.
Therefore, there are 4 degrees of freedom for treatment.
To know more about statistical technique, refer
https://brainly.com/question/30787558
#SPJ11
Which of the following sets is a partition of [0,3] (A) (0,1,3/2, 2,5/2} (B) (0,2,3} C) {1,2,3} (D) {0,2/11, 1, 2, 7/3, 8/3}
Answers
The set {0,2,3} is a partition of [0,3].
So, the answer is B
A partition of a set is a collection of non-empty subsets, which are mutually exclusive and exhaustive. In other words, each element of the original set is assigned to exactly one of the subsets in the partition.
Therefore, we can conclude that a partition should satisfy the following conditions:
All subsets in the partition are non-empty
.The intersection of any two distinct subsets in the partition is empty.
The union of all the subsets in the partition is equal to the original set.Let's examine each of the given sets to see which one is a partition of [0, 3].(A) {0,1,3/2, 2,5/2}
The set (A) contains the element 0, so it satisfies the first condition. However, it does not contain the element 3, which means it is not a subset of [0, 3]. Therefore, it cannot be a partition of [0, 3].(B) {0,2,3}
The set (B) contains the elements 0, 2, and 3, so it satisfies the first condition. It also satisfies the second condition because the intersection of any two distinct subsets is empty.
Finally, the union of the three subsets is [0, 3], which satisfies the third condition. Therefore, (B) is a partition of [0, 3].(C) {1,2,3}The set (C) does not contain the element 0, so it is not a subset of [0, 3]. Therefore, it cannot be a partition of [0, 3].(D) {0,2/11, 1, 2, 7/3, 8/3}The set (D) contains the element 0, so it satisfies the first condition. However, it contains the elements 2/11 and 8/3, which are not in [0, 3]. Therefore, it is not a subset of [0, 3]. Therefore, it cannot be a partition of [0, 3].
Thus, the correct option is (B) {0,2,3}.
Learn more about partition at:
https://brainly.com/question/31844329
#SPJ11