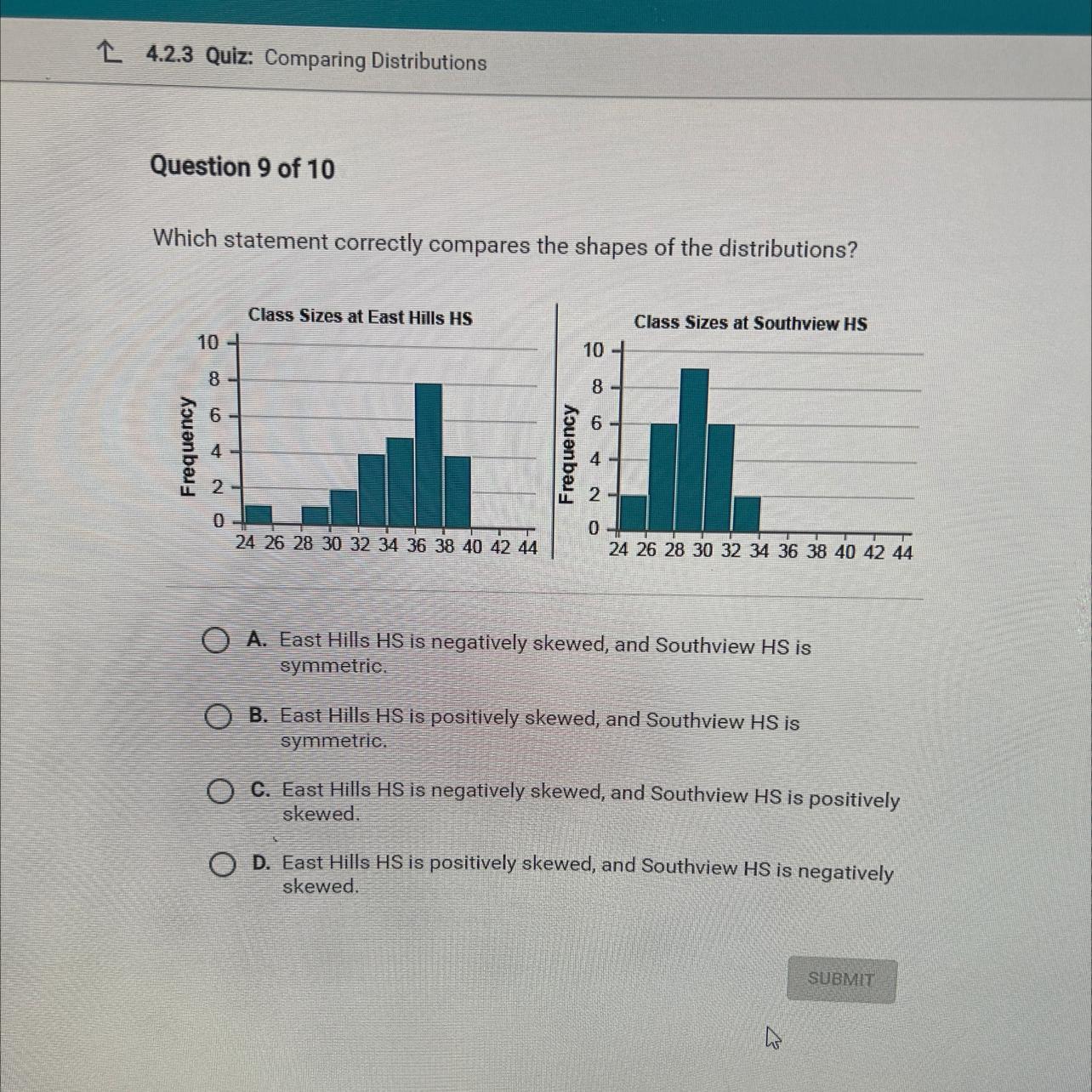
PLEASE HELPPPPP!!!!! Which statement correctly compares the shapes of the of the distributions!

The number of valid ways to construct the cube is [tex]4096 - 48 = 4048[/tex]

Each corner of the cube is formed by three wires coming together. Since the wires are soldered together at the ends, each corner must have either 3 silver wires or 3 copper wires coming together.

There are two choices for each wire: it can be silver or copper. Since there are 12 edges in a cube, there are 2 choices for each edge, giving a total of [tex]2^12 = 4096[/tex] possible arrangements of the edges.

However, not all of these arrangements are valid. We must eliminate the arrangements where at least one corner has two silver wires and one copper wire

There are 8 corners in a cube, and for each corner, there are 3 ways to choose which wire is different from the other two. Once we choose which wire is different, there are 2 choices for its color (silver or copper). Thus, there are [tex]8 x 3 x 2 = 48[/tex] invalid arrangements.

for such more questions on arrangements

https://brainly.com/question/1427391

#SPJ11

The chance/

probability

is

16/33

, or roughly 0.485 that 1 and 2 are in the

same set.

Let's say we divide the range of numbers from

1 to 15

into two sets, each containing seven and eight numbers, respectively. Finding the likelihood that the numbers 1 and 2 are included in the same

set

is our goal.

We can determine the

total number

of ways to divide the numbers into the two sets of

7

and

8

in order to begin solving this issue. Calculating this yields the result 6435 using a formula.

The number of ways in which the pairs 1 and 2 can be found in the same set must then be determined. Considering that there are

seven numbers

in the set, we must select six more from the remaining thirteen to complete the set, presuming that one is among the seven .There are

1716

ways to do this. The number of methods remains the same, 1716, even if we suppose that 2 is among the set of 7 numbers.

Hence, there are

3432

different ways to combine the numbers 1 and 2 into one set. The chance is 16/33, or roughly 0.485, when we divide this number by the total number of possible

divisions

of the numbers.

Learn more about

probability:

https://brainly.com/question/14210034

#SPJ4

$1000 is 71.43 percent of the credit limit.

To lower the debt to credit limit ratio by $1000, you have a few options. The first option is to increase your credit limit by requesting a higher limit from your credit card issuer. Alternatively, you can pay off some of your outstanding balance to reduce your debt. Either way, it's important to make sure you're not maxing out your credit limit, as this can negatively impact your credit score.

It's also a good idea to review your spending habits and create a budget to ensure you're not overspending and accumulating debt. By making responsible financial decisions and managing your credit wisely, you can improve your credit score and achieve your financial goals.

To calculate the percentage of $1000 in terms of the credit limit of $1400, we need to divide $1000 by $1400 and multiply the result by 100. This gives us,

($1000 / $1400) x 100 = 71.43%

Therefore, $1000 is approximately 71.43% of the credit limit of $1400.

To learn more about percent here:

https://brainly.com/question/30704720

#SPJ4

The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.

To find the extreme values of V, we need to take the derivative of V and set it equal to zero. So, let's begin:

[tex]V(x) = x(10-2x)(16-2x)[/tex]
Taking the derivative with respect to x:
[tex]V'(x) = 10x - 4x^2 - 32x + 12x^2 + 320 - 48x[/tex]
Setting V'(x) = 0 and solving for x:
[tex]10x - 4x^2 - 32x + 12x^2 + 320 - 48x = 0\\8x^2 - 30x + 320 = 0[/tex]
Solving for x using the quadratic formula:
[tex]x = (30 ± \sqrt{(30^2 - 4(8)(320))) / (2(8))\\x = (30 ± \sqrt{(1680)) / 16\\x = 0.93 or x =5.07[/tex]
So, the extreme values of V occur at x ≈ 0.93 and x ≈ 5.07. To determine whether these are maximum or minimum values, we need to examine the second derivative of V. If the second derivative is positive, then the function has a minimum at that point. If the second derivative is negative, then the function has a maximum at that point. If the second derivative is zero, then we need to use a different method to determine whether it's a maximum or minimum.

Taking the second derivative of V:
V''(x) = 10 - 8x - 24x + 24x + 96
V''(x) = -8x + 106

Plugging in x = 0.93 and x = 5.07:
V''(0.93) ≈ 98.36 > 0, so V has a minimum at x ≈ 0.93.
V''(5.07) ≈ -56.56 < 0, so V has a maximum at x ≈ 5.07.

Now, to interpret these values in terms of the volume of the box, we need to remember that V(x) represents the volume of a box with length 2x, width 2x, and height x. So, the maximum value of V occurs at x ≈ 5.07, which means that the volume of the box is greatest when the height is about 5.07 units. The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.

learn more about extreme values

https://brainly.com/question/1286349

#SPJ11

a) The extreme values of V are:

Minimum value: V(0) = 0

Relative maximum value: V(3) = 216

Absolute maximum value: V(4) = 128

b) The absolute maximum value of V at x = 4 represents the case where the box has a square base of side length 4 units, height 2 units, and width 8 units, which has a volume of 128 cubic units.

a) To find the extreme values of V, we first need to find the critical points of the function. This means we need to find where the derivative of the function equals zero or is undefined.

Taking the derivative of V(x), we get:

[tex]V'(x) = 48x - 36x^2 - 4x^3[/tex]

Setting this equal to zero and solving for x, we get:

[tex]48x - 36x^2 - 4x^3 = 0[/tex]
4x(4-x)(3-x) = 0

So the critical points are x = 0, x = 4, and x = 3.

We now need to test these critical points to see which ones correspond to maximum or minimum values of V.

We can use the second derivative test to do this. Taking the derivative of V'(x), we get:

[tex]V''(x) = 48 - 72x - 12x^2[/tex]

Plugging in the critical points, we get:

V''(0) = 48 > 0 (so x = 0 corresponds to a minimum value of V)
V''(4) = -48 < 0 (so x = 4 corresponds to a maximum value of V)
V''(3) = 0 (so we need to do further testing to see what this critical point corresponds to)

To test the critical point x = 3, we can simply plug it into V(x) and compare it to the values at x = 0 and x = 4:

V(0) = 0
V(3) = 216
V(4) = 128

So x = 3 corresponds to a relative maximum value of V.
b) In terms of the volume of the box, the function V(x) represents the volume of a rectangular box with a square base of side length x and height (10-2x) and width (16-2x).
The minimum value of V at x = 0 represents the case where the box has no dimensions (i.e. it's a point), so the volume is zero.
The relative maximum value of V at x = 3 represents the case where the box is a cube with side length 3 units, which has a volume of 216 cubic units.
for such more question on extreme values

https://brainly.com/question/30886356

#SPJ11

Answer:

-23. In my explanation I will include in my picture how this will look in your final answer

Step-by-step explanation:

So to solve this, I first set x + 3 = 0. This means that x = -3, which we will use soon. Now, here's how you would work out this problem. It would be confusing if I explained over text, so I included a picture of my work.

You would first set up your problem like it is in the picture. Then, bring 2 down. Next, multiply 2 by -3 (for future problems, you would multiply the number you brought down by whatever number is on the side). -3 × 2 = -6, so you would put that under 3 (as shown in the picture). Now, add 3 and -6 (which = -3). Repeat this step each time.

I hope this made sense! Please let me know if you have any questions.

The probability that the weight of a randomly selected newborn baby boy born at the local hospital will be greater than 2620 grams is 0.9099 (rounded to four decimal places).

The probability can be calculated using the standard normal distribution as follows:

P(Z > (2620 - 3245) / 625) = P(Z > -1.335)

Using a standard normal distribution table, we find that the probability of Z being greater than -1.335 is 0.9099.

We use the standard normal distribution because we know the mean and standard deviation of the population of newborn baby boys' weights. We convert the raw score of 2620 grams to a z-score, which tells us how many standard deviations the raw score is away from the mean.

Learn more about probability

https://brainly.com/question/24756209

#SPJ4

In the given equation r = 2/5 t "r" is the dependent variable.

In mathematics, a variable is a symbol that represents a quantity that can take on different values. In many cases, variables can be divided into two types: dependent variables and independent variables.

An independent variable is a variable that can be changed freely, and its value is not dependent on any other variable in the equation.

A dependent variable is a variable whose value depends on the value of one or more other variables in the equation

Here we have

Lin notices that the number of cups of red paint is always  2/5 of the total number of cups.

She writes the equation r = 2/5 t to describe the relationship.

In the equation, r = 2/5 t, "t" represents the total number of cups, while "r" represents the number of cups of red paint.

Here "t" is the independent variable because it represents the total number of cups, which can be changed arbitrarily.

The value of "r" depends on the value of "t" because the number of cups of red paint is always 2/5 of the total number of cups.

Therefore,

In the given equation r = 2/5 t "r" is the dependent variable.

Learn more about Variables at

https://brainly.com/question/1479694

#SPJ1

Complete Question:

Lin notices that the number of cups of red paint is always  2/5 of the total number of cups. She writes the equation r = 2/5 t to describe the relationship. Which is the independent variable? Which is the dependent variable? Explain how you know.

According to the equation, a person who weighs 63 kg is predicted to be approximately 141 centimeters tall.

The equation given is Y = 0.91X - 65.5, where X represents the height in centimeters and Y represents the weight in kilograms. To predict the height of a person who weighs 63 kg, we need to solve for X, the height in centimeters.

To do this, we can plug in the given weight of 63 kg for Y in the equation and then solve for X. So, we have:

63 = 0.91X - 65.5

Adding 65.5 to both sides, we get:

63 + 65.5 = 0.91X

Simplifying, we have:

128.5 = 0.91X

Finally, to solve for X, we divide both sides by 0.91, giving:

X = 141.21

To know more about equation here

https://brainly.com/question/10413253

#SPJ4

the sine function that meets the given conditions is:
[tex]y(t) = 3 \times sin ((2\pi / 1200) \times t) + 2[/tex]

Function with the given characteristics.

The terms and their definitions we need to consider:
Amplitude:

The maximum displacement from the midline (in this case, 3)
Midline:

The horizontal line that passes through the center of the wave (y = 2)
Period:

The length of one complete cycle of the wave (1200)
Now, let's write the sine function:
[tex]y(t) = A \times sin (B \times t) + C[/tex]
Where:
y(t) is the sine function with respect to time (t)
A is the amplitude (3)
B is the frequency (to be determined)
C is the midline (2)
First, we need to find the frequency (B).

The period and frequency are related by the following formula:
[tex]Period = 2\pi / B[/tex]
In this case, the period is 1200:
[tex]1200 = 2\pi / B[/tex]
Now, solve for B:
[tex]B = 2\pi / 1200[/tex]
Now, we can plug in the amplitude (A), frequency (B), and midline (C) into our sine function:
[tex]y(t) = 3 \times sin((2\pi / 1200) \times t) + 2[/tex]

For similar questions on Function

https://brainly.com/question/11624077

#SPJ11

If the area of the base is 19. 6 ft^2 and the height of the pyramid is 11. 6 ft, the volume of the pyramid is approximately 79.1 cubic feet.

The formula for the volume of a pyramid is given by:

V = (1/3) × base area × height

In this case, we are given that the pyramid has a square base, so the base area is simply the area of a square with side length s:

base area = s^2 = 19.6 ft^2

We are also given the height of the pyramid:

height = 11.6 ft

Substituting these values into the formula for the volume of a pyramid, we get:

V = (1/3) × base area × height

= (1/3) × 19.6 ft^2 × 11.6 ft

≈ 79.1 ft^3 (rounded to the nearest tenth)

To learn more about volume click on,

https://brainly.com/question/23861754

#SPJ4

If p is a prime number and a is a positive integer, then pa has (a+1) distinct positive divisors.

A prime number is a positive integer greater than 1, which is divisible only by 1 and itself. Divisors are the numbers that evenly divide a given number.

For a prime number p raised to the power of a (p^a), the number of distinct positive divisors can be found using the following formula:

Number of divisors = (a + 1)

This is because each power of p from 0 to a can divide p^a without any remainder, giving us a total of a + 1 distinct divisors. These divisors are:

1, p, p^2, p^3, ..., p^(a-1), p^a

For example, if p = 2 (a prime number) and a = 3 (a positive integer), then the number of distinct positive divisors for 2^3 (which is 8) would be:

Number of divisors = (3 + 1) = 4

The divisors for 2^3 (8) are 1, 2, 4, and 8.

Learn more about Prime numbers here: brainly.com/question/30358834

#SPJ11

The result for the appropriate measure, relative risk, is approximately 0.515.

This indicates that the risk of death within 5 years is about 51.5% lower in the new procedure group compared to the standard procedure group.

This suggests a strong association between the surgical procedure and the reduction in the risk of death.

To determine the strength of the association between the surgical procedures and death, we can calculate the relative risk.
Identify the numbers given in the question.
- Total participants: 550
- New procedure group: 275 (half of 550)
- Deaths in new procedure group: 98
- Standard procedure group: 275 (half of 550)
- Deaths in standard procedure group: 190
Calculate the death rate (proportion of deaths) in each group.
- Death rate in new procedure group = (Number of deaths in new procedure group) / (Total in new procedure group) = 98/275 ≈ 0.356
- Death rate in standard procedure group = (Number of deaths in standard procedure group) / (Total in standard procedure group) = 190/275 ≈ 0.691
Calculate the relative risk.
- Relative risk = (Death rate in new procedure group) / (Death rate in standard procedure group) = 0.356/0.691 ≈ 0.515.

For similar question on standard.

https://brainly.com/question/187506

#SPJ11

194 member voted against the bill whereas 241 members voted in favour of the bill.

A bill usually refers to a piece of paper money, such as a dollar bill or a euro bill.

To solve this problem, we can use algebra. Let's call the number of members who voted against the bill "x". Then, the number of members who voted in favor of the bill would be "x + 47" (since there were 47 more members voting in favor than against).

We know that the total number of members who voted (either for or against) was 435. So, we can write an equation:

x + (x + 47) = 435

Simplifying this equation, we get:

2x + 47 = 435

Subtracting 47 from both sides:

2x = 388

Dividing both sides by 2:

x = 194

So, 194 members voted against the bill, and the number of members who voted in favor would be:

x + 47 = 194 + 47 = 241

Therefore, 241 members voted in favor of the bill.

Learn more about equation here:

https://brainly.com/question/10413253

#SPJ1

The best prediction possible for the number of times the spinner will land on green or blue is given as follows:

30 spins.

A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.

Out of six regions, three are green and two are blue, hence the probability of one spin resulting in green or blue is given as follows:

p = (3 + 2)/6

p = 5/6.

Thus the expected number out of 36 trials of spins resulting in green or blue is given as follows:

E(X) = 5/6 x 36

E(X) = 30 spins.

More can be learned about probability at https://brainly.com/question/24756209

#SPJ1

Assuming a two-tailed test with 9 degrees of freedom (10 stores minus 1), the p-value for a t-value of 2.3 is approximately 0.040.

In order to calculate the p-value, we need to know the specific test being used and the significance level of the test. Let's assume that the test is a two-tailed t-test with a significance level of 0.05.

Since the test statistic is 2.3, we need to find the probability of getting a t-value of 2.3 or greater (in absolute value) under the null hypothesis. We can use a t-distribution table or a statistical software to find the corresponding p-value.

Assuming a two-tailed test with 9 degrees of freedom (10 stores minus 1), the p-value for a t-value of 2.3 is approximately 0.040. Therefore, if the significance level of the test is 0.05, we would reject the null hypothesis and conclude that there is a significant difference between the ratings given by the three reviewers.

To know more about statistic here

https://brainly.com/question/15525560

#SPJ4

Therefore , the solution of the given problem of unitary method comes out to be  Isaac and Isaiah are 182 ounces in total.

Use the tried-and-true fundamental method, the actual variables, and any relevant information gleaned from general and specific questions to complete expression the assignment. Customers may be given another chance to taste the products in response. If these adjustments don't happen, we'll lose out on significant advancements in our understanding of programmes.

Here,

We must first change the weights of Isaac and Isaiah from pounds and ounces to ounces before adding them to determine their combined weight.

Weight of Isaac: six pounds 2 ounces = 6 * 16 + 2

= 96 + 2

= 98 ounces

Isaiah is 5 pounds in weight.

= 5 * 16 + 4

= 80 + 4

= 84 ounces

Together, Isaac and Isaiah weighed

98 ounces + 84 ounces = 182 ounces

As a result, Isaac and Isaiah are 182 ounces in total.

To know more about unitary method visit:

https://brainly.com/question/28276953

#SPJ1  

Answer:

The given function is k(t) = cos(2πt/3).

The general form of a cosine function is A*cos(Bx - C) + D, where:

Comparing this form to the given function, we can see that:

Therefore, the amplitude of k(t) is 1, the period of k(t) is 3, the phase shift of k(t) is 0, and the vertical shift of k(t) is 0.

Sample size and sample standard deviation are the key information needed for a single-sample t-test.

In the event that you need to compare the test cruel with the populace cruel, and you perform a single-sample t-test rather than a z-test, the vital piece of data that will be lost is the populace standard deviation.

Within the z-test, the populace standard deviation is known and the standard mistake of the cruel is calculated utilizing the populace standard deviation.

In a single-sample t-test, the populace standard deviation is obscure, and the standard mistake of the cruel is evaluated from the test standard deviation. 

Therefore, sample size and sample standard deviation are the key information needed for a single-sample t-test. 

learn more about standard deviation

brainly.com/question/23907081

#SPJ4

Applying the right triangle altitude theorem and the leg rule, we have:

5. x = 6; y ≈ 6.7; z ≈ 13.4       6. x = 32; y ≈ 35.8; z ≈ 17.9

The right triangle altitude theorem states that the altitude drawn on the hypotenuse of a right triangle is equal to the geometric mean of the two line segments into which the altitude divides the hypotenuse.

5. To find x, apply the right triangle altitude theorem, which is:

x = √(3*12)

x = √36

x = 6

Using the leg rule, we can find y and z. It is expressed as:

hypotenuse/leg = leg/part

Therefore, substitute and find y:

(3 + 12) / y = y / 3

Cross multiply:

y² = 15 * 3

y = √45

y ≈ 6.7

Find z using the leg rule:

15/z = z/12

z² = 180

z = √180

z ≈ 13.4

6. Use the same theorem and leg rule as done in question 5:

Find x:

16 = √(8 * x)

16² = 8x

256 = 8x

x = 256/8

x = 32

Find y using the leg rule:

(8 + 32) / y = y/32

y² = 40 * 32

y = √1,280

y ≈ 35.8

Find z:

40/z = z/8

z² = 40 * 8

z = √320

z ≈ 17.9

Learn more about the right triangle altitude theorem on:

https://brainly.com/question/31068781

#SPJ1

The greatest number of 27-inch pieces that she can cut from three pieces of ribbon is found to be 19. So, option B is the correct answer choice.

Each yard is equal to 36 inches, so 5 yards are equal to 180 inches. Therefore, each piece of ribbon is 180 inches long.

To find out how many 27-inch pieces Lucia can cut from each piece of ribbon, we divide 180 by 27.

180/27 = 6.67

Since Lucia can only cut whole pieces, she can cut 6 pieces of ribbon from each piece of ribbon.

Therefore, she can cut a total of 6 x 3 = 18 pieces of ribbon from the three separate pieces of ribbon.

Learn more about Division :

https://brainly.com/question/19871608

#SPJ4

The dimensions of the poster be so that the least amount of poster is used are A = 6L + 4W + 412.

Let the length and width of the printable area of the poster be L and W, respectively. Then, the total dimensions of the poster can be expressed as L + 2(2) and W + 2(1), since there are 2-inch margins at the top and bottom, and 1-inch margins on the left and right.

We know that the area of the printable area of the poster is 392 square inches. Therefore, we can write the equation: LW = 392

We want to minimize the total area of the poster, which is given by:

A = (L + 2(2))(W + 2(1)) = (L + 4)(W + 2)

Expanding this expression, we get:

A = LW + 2L + 4W + 8

Substituting the equation for LW, we get:

A = 392 + 2L + 4W + 8

Simplifying, we get:

A = 2L + 4W + 400

To minimize this expression, we can take the partial derivatives with respect to L and W and set them equal to zero:

[tex]∂A/∂L = 2 = 0 => L = 0[/tex]

[tex]

∂A/∂W = 4 = 0 => W = -100[/tex]

These values do not make sense in the context of the problem. Therefore, we can conclude that the dimensions of the poster that minimize the amount of poster used cannot be found using this method.

Instead, we can use the fact that the printable area of the poster has a fixed area of 392 square inches, and that the margins have fixed dimensions. We can express the area of the poster as:

A = (L + 4)(W + 2) = LW + 4L + 2W + 8

Substituting the equation for LW, we get:

A = 392 + 4L + 2W + 8

Simplifying, we get:

A = 4L + 2W + 400

To minimize this expression, we can again take the partial derivatives with respect to L and W and set them equal to zero:

[tex]∂A/∂L = 4 = 0 => L = 0[/tex]

[tex]∂A/∂W = 2 = 0 => W = -200[/tex]

These values do not make sense in the context of the problem. Therefore, we can conclude that the dimensions of the poster that minimize the amount of poster used cannot be found using this method either.

We can try a different approach. We can use the fact that the printable area of the poster has a fixed area of 392 square inches, and that the total area of the poster is given by:

A = (L + 4)(W + 2) + 2(L + 4) + 2(W + 2)

Expanding this expression, we get:

A = LW + 6L + 4W + 20

Substituting the equation for LW, we get:

A = 392 + 6L + 4W + 20

Simplifying, we get: A = 6L + 4W + 412

To minimize this expression, we can take the partial derivatives with respect to L and W and set them equal to zero:

[tex]∂A/∂L = 6 = 0 => L = -2/3[/tex]

[tex]∂A/∂W = 4 = 0 => W = -3/2[/tex]

Learn more about dimensions here:

https://brainly.com/question/29581656

#SPJ4

Step-by-step explanation:

24 times, as there are no orange marbles in the set.

so, every pull will produce a marble that is not orange with 100% certainty.

in general, we have 12 marbles.

let's change the problem description into picking a marbles that is not blue.

we have 6 blue marbles.

the chance to pick a blue marble is therefore 6/12 = 1/2.

and the probability to not pick a blue marbles is 1 - 1/2 = 1/2.

so, in 24 pulls, we expect 24× 1/2 = 12 times to get a marble that is not blue.

or change it to "not green" marbles.

5 green marbles.

the probability to pick a green marble is 5/12.

the probabilty to not pick a green marble = 1 - 5/12 = 7/12.

in 24 pulls we expect 24 × 7/12 = 14 times to get a marble that is not green.

it change it to "not purple" marbles.

1 purple marble.

the probability to pick a purple marble is 1/12.

the probabilty to not pick a purple marble = 1 - 1/12 = 11/12.

in 24 pulls we expect 24 × 11/12 = 22 times to get a marble that is not purple.

Step-by-step explanation:

vf = vo + at      vo = 0 in this case  ( you dropped it from 'at rest')

4 f/s = 32 t

t = 1/8 s

df = do + vot + 1/2 at^2                  df = final position = 0 ft (on the ground)

0 = do  + 0   + 1/2 (-32)(1/8)^2

   solve for do = 1/4 foot

The pair of required complementary angles are 26.2° and 63.8° respectively.

Two angles are said to be supplementary angles because they combine to generate a linear angle when their sum is 180 degrees.

When two angles add up to 90 degrees, however, they are said to be complimentary angles and together they make a right angle.

If the total of two angles is 90o (ninety degrees), then the angles are complementary.

A 30-angle and a 60-angle, for instance, are two complementary angles.

So, to find the 2 angles which are complementary:

x + x + 37.6 = 90

Now, solve it as follows:

x + x + 37.6 = 90

2x = 90 - 37.6

2x = 52.4

x = 52.4/2

x = 26.2

Now, x = 26.2 and the second angle x + 37.6 is = 26.2 + 37.6 = 63.8°.

Therefore, the pair of required complementary angles are 26.2° and 63.8° respectively.

Know more about complementary angles here:

https://brainly.com/question/16281260

#SPJ1

The total areas of each composite shape are:

1) 121 in²

2) 150m²

3) 14.03 ft²

4) 538.36 cm²

1) Formula for area of a rectangle is:

Area = Length * width

Thus:

Area of composite shape = (9 * 8) + (7 * 7)

= 121 in²

2) Formula for area of rectangle is:

Area = Length * width

Area = 12 * 5 = 60 m²

Area of triangle = ¹/₂ * base * height

Area = ¹/₂ * 12 * 15

Area = 90 m²

Area of composite shape = 60 + 90 = 150m²

3) Area of triangle = ¹/₂ * 3 * 7 = 10.5 ft²

Area of semi circle = ¹/₂ * πr²

= ¹/₂ * π * 1.5²

= 3.53 ft²

Total composite area = 10.5 ft² + 3.53 ft²

Total composite area = 14.03 ft²

4) Total composite area = (¹/₂ * π * 7.5²) + (30 * 15)

= 538.36 cm²

Read more about Area of composite figure at: https://brainly.com/question/10254615

#SPJ1

Answer:

To find the average rate of change of the function f(x) = 1.5x² over the interval [10, 11], we need to calculate the change in f(x) over the interval, and divide by the change in x.

The change in f(x) over the interval [10, 11] is:

f(11) - f(10) = (1.511^2) - (1.510^2) = 165 - 150 = 15

The change in x over the interval [10, 11] is:

11 - 10 = 1

Therefore, the average rate of change of the function over the interval [10, 11] is:

(15/1) = 15

This means that for every 1 cm increase in diameter (i.e., for every 1 unit increase in x), the number of calories in the pancake increases by an average of 15 calories per cm of diameter.

Therefore, the answer is (A) 150 calories per cm of diameter.

Answer:

Step-by-step explanation:

6 greater than a number is 24.

This means adding 6 to a number, x, will equal 24.

6 + x = 24

subtract 6 from both sides of the equation, and you are left with x=18

18 is your answer!!

Triangle PQR's perimeter is **60 inches**.

The lengths of a triangle's sides added together form its perimeter.

The Pythagorean theorem asserts that in a right-angled triangle, the square of the hypotenuse's length (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides 1. A Pythagorean triplet is a group of three positive integers that satisfies this condition.

Triangle PQR has sides PQ = 15 inches, QR = 20 inches, and PR = 25 inches.

A triangle's perimeter is equal to the sum of its sides. Triangle PQR's perimeter is 15 + 20 + 25= **60 inches**.  as a result.

To know more about perimeter of triangle visit:

brainly.com/question/29507476

#SPJ1

The property used to simplify the expression is the Commutative Property of Addition, which states that changing the order of addends does not change the sum.

The Commutative Property is a property of operations that states that the order in which two numbers are added or multiplied does not affect the result. In other words, the property says that changing the order of the terms being added or multiplied will not change the final answer.

The property that was used to simplify the expression is the Commutative Property of Addition. This property states that the order in which we add two numbers does not affect the result. In other words, if we have two numbers a and b, then a + b is equal to b + a.

In the given expression, we have two terms, 3c and 4c, that are being added together. By applying the Commutative Property of Addition, we can rearrange the terms to get 4c + 3c. This gives us the simplified expression 7c + 9.

To know more about Commutative Property visit:

https://brainly.com/question/778086

#SPJ1