Question 1 (10 marks)
Tom is preparing for a 100 meters race competition. During his practice last week, a sample of seven 100
meters races is reviewed, and the finishing times (in seconds) were as below:
13.4
15.6
13.1
14.5
14.2
13.3
15.3
It is reasonable to assume his finishing times are normally distributed.
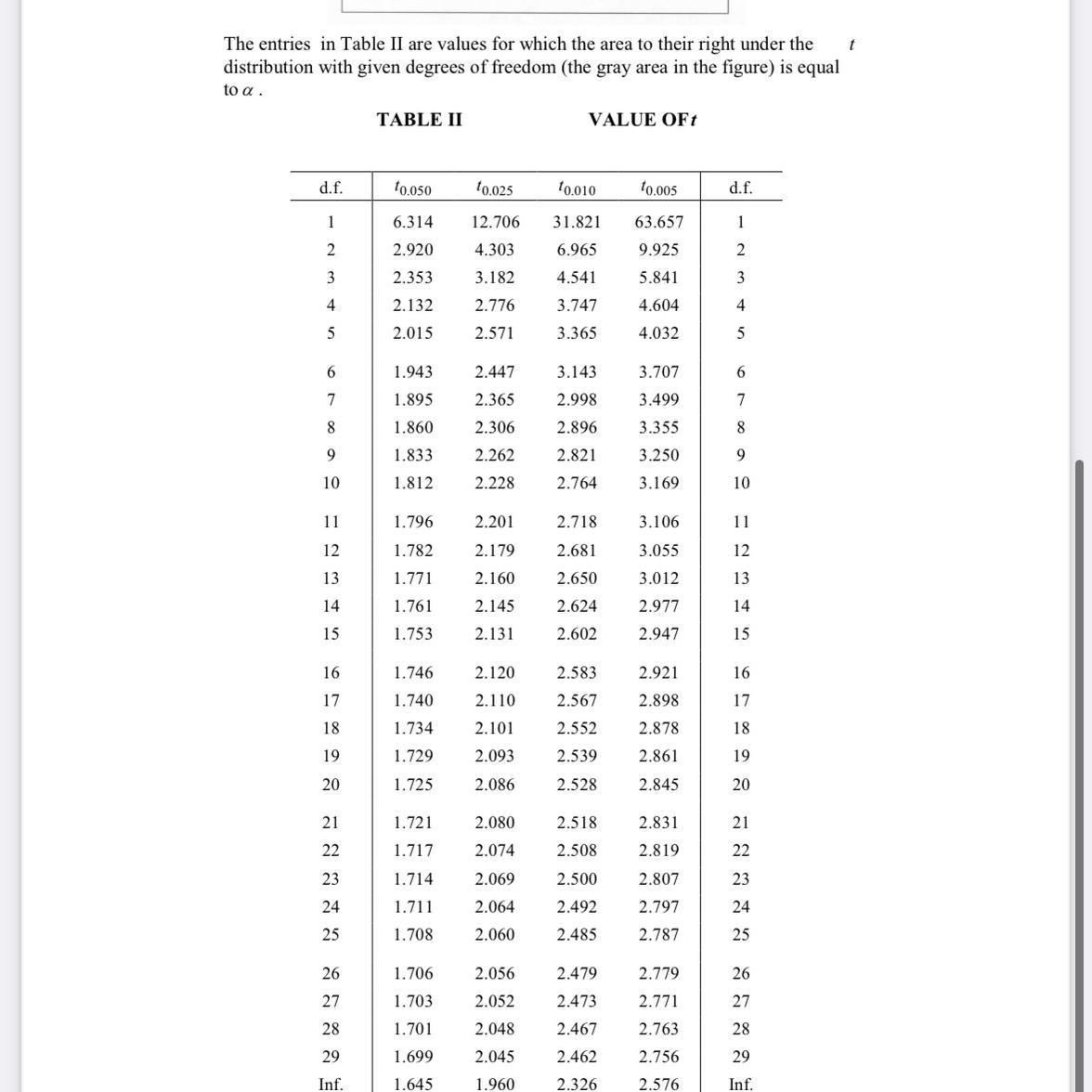
(a) Construct a 99% confidence interval estimate of his population mean finishing time of 100 meters race.
(b) If the confidence interval estimate of his population mean finishing time of 100 meters is constructed at
95% instead of 99%, would the new confidence interval be (I) wider, (II) narrower, or (III) the same as
the interval constructed at part (a)? (Just state your answer, no calculation is needed in part (b))
Question 2 (20 marks)
A survey was conducted one month ago to review the calories of lunch boxes provided by the supplier "Better
Lunch". In a sample with 300 lunch boxes, there were 273 lunch boxes with calories below 650 and the other
27 lunch boxes with calories above 650. Besides, the mean calories was 550 and standard deviation was 40.
(a) Find the point estimate of the population proportion of lunch boxes provided by "Better Lunch" had
calories above 650.
(b) Calculate the sampling error at 98% confidence level for the estimate of the population proportion of
lunch boxes provided by "Better Lunch" had calories above 650.
(c) Construct a 98% confidence interval estimate of the population proportion of lunch boxes provided by
"Better Lunch" had calories above 650.
(d) "Better Lunch" follows government's suggestions to change the menu in order to reduce the lunch boxes'
calories. Suppose after the menu update, each lunch box's calories can be reduced by 4%. Find the
sample mean and sample standard deviation of calories of the above sample after the change. Hence,
construct a 90% confidence interval estimate of the population mean calories in a lunch box after the
change.

Answer:

[tex]3( {2}^{2} ) - {2}^{2} + 4 = 12[/tex]

[tex] {2}^{3} + b( {2}^{2} ) + 43(2) - 126 = 4b - 204[/tex]

[tex]4b - 32 = 12[/tex]

[tex]4b = 44[/tex]

[tex]b = 11[/tex]

For this value of b, these graphs will intersect at (2, 12). Please use your graphing calculator to confirm that this is the only point of intersection.

Answer:

$5040

Step-by-step explanation:

Apply the formula

SI = (Principal)(Rate)(Time)

= 6000×0.12×7

= $5,040

Answer: 4.8%

Step-by-step explanation: the total amount of pens in the drawer is (10+12+3)  = 25

the amount of red pens in the drawer is 3

the probability of picking out a red pen from the drawer = 3/25

the amount of blue pens in the drawer is 10

the probability of picking out a red pen from the drawer = 10/25

the probability of picking out a red pen then a blue pen afterwards = (10/25 x 3/25) = 4.8%

There are 52 quarters and 15 half-dollars

Let's represent the number of half-dollars as "x" and the number of quarters as "y".

From the problem statement, we know that:

x + y = 67 (because there are a total of 67 coins)

y = 3x + 7 (because the number of quarters is 7 more than three times the number of half-dollars)

We can use substitution to solve for x:

x + (3x + 7) = 67

4x + 7 = 67

4x = 60

x = 15

So there are 15 half-dollars. We can use this to find the number of quarters:

y = 3x + 7

y = 3(15) + 7

y = 52

So there are 52 quarters.

Therefore, there are 52 quarters and 15 half-dollars.

Learn more about substitution here : brainly.com/question/26094713

#SPJ1

Answer:

Try using Special Right Triangles

Step-by-step explanation:

I think it is a carry-on of special right triangles. Since it is 90 degrees let's just assume it is a 60,30,90 triangle. we know the long leg is 6 from the x-6 on the bottom left, and 4rad3 is the hypotenuse.

Long leg: rad 3

Short leg: 1

Hypotenuse: 2

use these ratios to help

I would put 4rad3 across from 2 and y across from 1

aka: 4rad3/y = 2/1

also 4rad3 across from 2 and x across from rad 3

aka:4rad3/x=2/rad3

to find y you simplify

and

to find x also simplify

According to the given information, the function has no cusp.

What is a function?

A function is a relation between a set of inputs and a set of possible outputs, with the property that each input is related to exactly one output.

The given piecewise function is:

c(x) = 39, when x ≤ 6

c(x) = 39 + 5(x - 6), when x > 6

A cusp is a point on the graph where the function changes direction very abruptly, like a sharp turn. This happens when the derivative of the function is not defined at that point.

The derivative of the function is:

c'(x) = 0, when x ≤ 6

c'(x) = 5, when x > 6

Since the derivative is defined and continuous at x = 6, there is no cusp at that point. Therefore, the function has no cusp.

To know more about functions visit:

brainly.com/question/29120892

#SPJ1

The composite functions (f/g)(x) and (f-g)(x) are (2x-1)/√(3x-5) and (2x-1) -√(3x-5)

To calculate (f/g)(x), we need to divide f(x) by g(x):

(f/g)(x) = f(x)/g(x) = (2x-1)/√(3x-5)

The domain of (f/g)(x) is the set of all x-values for which the denominator √(3x-5) is not equal to zero and non-negative

3x-5 ≥ 0, or x ≥ 5/3

Therefore, the domain of (f/g)(x) is x ≥ 5/3.

To calculate (f-g)(x), we need to subtract g(x) from f(x):

(f-g)(x) = f(x) - g(x) = (2x-1) - √(3x-5)

The domain of (f-g)(x) is the set of all x-values for which the expression inside the square root is non-negative:

3x-5 ≥ 0, or x ≥ 5/3

Therefore, the domain of (f-g)(x) is x ≥ 5/3.

Read more about composite function at

https://brainly.com/question/10687170

#SPJ1

The polynomial function of least degree that has zeros of x=0, x=2i, and x=3, and with all coefficients real is:

Since the zeros of the polynomial function are given as

x=0, x=2i, and x=3,

we can write the function in factored form as follows:

f(x) = a(x-0)(x-2i)(x-3)

where

a is a constant coefficient and the factors correspond to the given zeros.

Since all coefficients must be real, we know that the complex conjugate of 2i, which is -2i, must also be a zero of the function. Therefore, we can rewrite the function as:

f(x) = a(x-0)(x-2i)(x+2i)(x-3)

Expanding this expression gives:

f(x) = a(x² + 4)(x-3)

Multiplying out the brackets and collecting like terms, we get:

f(x) = ax³ - 3ax² + 4ax - 12a

To find the value of 'a', we can use the fact that the coefficient of the x³ term is 1. Thus, we have:

a = 1/(1*4) = 1/4

Substituting this value of 'a' in the above expression, we get:

f(x) = (1/4)x³ - (3/4)x² + x - 3

Therefore, the polynomial function of least degree that has zeros of x=0, x=2i, and x=3, and with all coefficients real is:

Option A: f(x) = x² - 3x³ + 4x² - 12x

Learn more about polynomial function at

https://brainly.com/question/2833285

#SPJ1

Answer:

finding the perimeter, you sumthe distance all round that is 7+7.5+17.8+6=38.3

38.3 is the perimeter

Step-by-step explanation:

36^3/4   *    36 ^-1/4    =   36 ^( 3/4 - 1/4 )  =  36 ^1/2 = sqrt (36 ) = 6

option D 20  is correct answer .the perimeter of polygon XYDB is 20.

what is  polygon ?

A polygon is a closed geometric shape made up of straight line segments connected end-to-end. It is a two-dimensional figure that has three or more sides and angles. Polygons can be classified according to the number of sides

In the given question,

To find the perimeter of polygon XYDB, we need to add up the lengths of all its sides. Since all side lengths are given as 5, we can simply multiply 5 by the number of sides to get the perimeter.

Polygon XYDB has four sides, so the perimeter is:

Perimeter = 4 × 5 = 20

Therefore, the perimeter of polygon XYDB is 20.

To know more about  polygon , visit:

https://brainly.com/question/28276384

#SPJ1

Answer:

D. 20 cm

Step-by-step explanation:

In triangle ABC

a) The value of x = 29⁰

b) The angle c equal to 93⁰

A triangle is a closed plane figure that is formed by connecting three line segments, also known as sides, at their endpoints. The three endpoints, or vertices, where the sides of the triangle meet are not collinear. Triangles are important in mathematics and geometry because they are the simplest polygon that can exist in two-dimensional space.

In a triangle, the sum of all interior angles is always 180 degrees. Therefore, we can use this fact to find the value of x and angle c.

We know that:

angle a = 35⁰

angle b = 52⁰

angle c = 3(x+2)⁰

Using the fact that the sum of all interior angles in a triangle is 180 degrees, we can write:

angle a + angle b + angle c = 180

Substituting the values we know, we get:

35 + 52 + 3(x+2) = 180

Simplifying the equation, we get:

87 + 3x + 6 = 180

3x + 93 = 180

3x = 87

x = 29

Therefore, x = 29⁰

To find angle c, we can substitute the value of x into the equation we were given for angle c:

angle c = 3(x+2)

angle c = 3(29+2)

angle c = 3(31)

angle c = 93

Therefore, angle c is equal to 93⁰.

To know more about interior angles visit:

brainly.com/question/12834063

#SPJ1

The intervals on which the function Is constant are [-4, -3] and [3, 6]

A function is considered constant over an interval if the function has the same output for all the inputs within that interval.

In other words, the function does not change over that interval.

Using the above as a guide, we have the following:

The function does not change over the intervals [-4, -3] and [3, 6]

Hence, the intervals are [-4, -3] and [3, 6]

Read more about functions at

https://brainly.com/question/28532394

#SPJ1

Arun's purple paint will be redder.

Percentage is a way of expressing a proportion or a fraction as a number out of 100. It is represented by the symbol "%". For example, if you say that 20% of students in a class scored an A grade in a test, it means that 20 out of every 100 students received an A grade.

Deondra mixed 6 cups of blue paint and 7 cups of red paint, so the percent of red paint in her mixture is:

7 / (6 + 7) × 100% = 53.8%, which rounds to 54%.

Arun mixed 2 cups of blue paint and 3 cups of red paint, so the percent of red paint in his mixture is:

3 / (2 + 3) × 100% = 60%.

Since Arun's mixture has a higher percentage of red paint, his purple paint will be redder than Deondra's.

Therefore, the answer is Arun's purple paint will be redder.

To know more about fraction, visit:

https://brainly.com/question/10354322

#SPJ1

The equation of the normal plane is 4y = 4π, or equivalently, y = π.

The word osculate comes from the Latin osculatus, which is a past participle of the verb osculari, which means "to kiss." Thus, an osculating plane is one that "kisses" a submanifold.

To find the osculating plane and normal plane of the curve x = sin 2t, y = t, z = cos 2t at the point (0, π, 1), we need to follow these steps:

Step 1: Find the first and second derivatives of the curve with respect to t.

x' = 2cos2t

y' = 1

z' = -2sin2t

x'' = -4sin2t

y'' = 0

z'' = -4cos2t

Step 2: Evaluate the derivatives at t = π.

x'(π) = 2cos2π = 2

y'(π) = 1

z'(π) = -2sin2π = 0

x''(π) = -4sin2π = 0

y''(π) = 0

z''(π) = -4cos2π = -4

So the velocity vector at the point (0, π, 1) is v = ⟨2, 1, 0⟩, the acceleration vector is a = ⟨0, 0, -4⟩, and the curvature vector is κv = ⟨0, 4, 0⟩.

Step 3: Use the velocity and acceleration vectors to find the normal vector of the osculating plane.

The normal vector of the osculating plane is given by the cross product of the velocity and acceleration vectors:

n = v × a = ⟨2, 1, 0⟩ × ⟨0, 0, -4⟩ = ⟨4, 0, 0⟩

Step 4: Use the normal vector and the point (0, π, 1) to find the equation of the osculating plane.

The equation of the osculating plane is given by:

4(x - 0) + 0(y - π) + 0(z - 1) = 0

Simplifying, we get:

4x - 4 = 0

So the equation of the osculating plane is 4x = 4, or equivalently, x = 1.

Step 5: Use the curvature vector to find the normal vector of the normal plane.

The normal vector of the normal plane is given by the curvature vector:

n' = κv = ⟨0, 4, 0⟩

Step 6: Use the normal vector and the point (0, π, 1) to find the equation of the normal plane.

The equation of the normal plane is given by:

0(x - 0) + 4(y - π) + 0(z - 1) = 0

Simplifying, we get:

4y - 4π = 0

So, the equation of the normal plane is 4y = 4π, or equivalently, y = π.

Learn more about derivatives on:

https://brainly.com/question/23819325

#SPJ1

the area of the trapezoid is 10√3 km² (approximately 17.3 km²).To find the area of a trapezoid, we use the formula A = (1/2) * (b₁ + b₂) * h

what is trapezoid ?

A trapezoid is a quadrilateral with at least one pair of parallel sides. The parallel sides are called the bases of the trapezoid, and the other two sides are called the legs. The height (or altitude) of a trapezoid is the perpendicular distance between the two bases. The formula for the area of a trapezoid

In the given question,

To find the area of a trapezoid, we use the formula:

A = (1/2) * (b₁ + b₂) * h

where A is the area, b₁ and b₂ are the lengths of the parallel sides of the trapezoid, and h is the height (or perpendicular distance between the parallel sides).

In this case, we are not given the height, but we can still find the area if we make some assumptions. Let's assume that the trapezoid is isosceles, which means that the two non-parallel sides are equal in length. Then we can draw an altitude from one of the vertices to the opposite base, which will bisect the base and create two right triangles.

Using the Pythagorean theorem, we can find the length of the altitude:

a² + (b₁ - b₂)² = (2a)²

Simplifying and solving for a, we get:

a² + (b₁- b₂)² = 4a²

3a² = (b₁ - b₂)²

a = (1/√3) * |b₁ - b₂|

Since we know that the sum of the non-parallel sides is 10 km, we can write:

b₁ + b₂ = 10

Let's assume that b1 is the longer base, so we can write:

b₁ = 8 km

b₂ = 10 - b₁ = 2 km

Substituting these values into the formula for the altitude, we get:

a = (1/√3) * |8 - 2| = (1/√3) * 6 = 2√3 km

Now we can use the formula for the area of a trapezoid to find the area:

A = (1/2) * (b1 + b2) * h

A = (1/2) * (8 + 2) * 2√3

A = 10√3 km²

Therefore, the area of the trapezoid is 10√3 km² (approximately 17.3 km²).

To know more about trapezoid , visit:

https://brainly.com/question/8643562

#SPJ1

Therefore, Dorie needs to sell the dress for $349.93 in order to mark it back to its regular selling price.

What is selling price?

Selling price refers to the price at which a product or service is sold to customers. It is the amount of money that a buyer pays to the seller in exchange for the product or service. The selling price is usually higher than the cost price, which is the amount that the seller paid to acquire or produce the product or service. The difference between the selling price and the cost price is called the profit margin, and it is the profit that the seller makes on the sale of the product or service.

If a dress had been marked down 70%, this means that it is being sold for only 30% of its original selling price.

Let P be the original selling price of the dress. Then:

0.3P = $104.98

Solving for P, we get:

P = $104.98 / 0.3

P = $349.93

Therefore, Dorie needs to sell the dress for $349.93 in order to mark it back to its regular selling price.

To know more about selling price, visit:

https://brainly.com/question/28017453

#SPJ1

Answer: 5 were triangles :)

The correct answer is (1,1) because both of the lines meet together at these numbers

The function is nonlinear because the variable x is raised to the second power. So, the correct option is D) .

A linear function is a mathematical equation that can be represented by a straight line. It is a function in which the independent variable, say "x," is raised only to the first power, and the dependent variable, say "y," is not multiplied or divided by any variable. Linear functions have a constant rate of change, which means that the slope of the line is the same at all points.

The general form of a linear function is y = mx + b, where m is the slope of the line and b is the y-intercept, which is the point at which the line crosses the y-axis. The slope m represents the rate of change of y with respect to x, and can be calculated as the change in y divided by the change in x between any two points on the line.

A linear function is a function that has a constant rate of change, meaning that as x increases by a certain amount, y also increases by a constant amount. A linear function can be written in the form y = mx + b, where m is the slope and b is the y-intercept.

In the given equation y = x²  + 9, the variable x is raised to the second power, which means that the rate of change of y with respect to x is not constant. This is the characteristic of a nonlinear function. Moreover, the graph of the function is a parabola, which is also a characteristic of a nonlinear function.

Therefore, the correct answer is D) The function is nonlinear because the variable x is raised to the second power.

To know more about parabola visit:

https://brainly.com/question/24164631

#SPJ1

The complete question is :

Which statement explains the type of function that is represented by the equation y=x² +9?

A The function is linear because it contains more than one term.

B) The function is linear because the variable x is raised to the second power.

C) The function is nonlinear because it contains more than one term.

D) The function is nonlinear because the variable x is raised to the second power.

The value of p(B/A) represents the probability that event B will occur given that event A has occurred.

It is a measure of conditional probability, which is calculated using the formula:

p(B/A) = p(A ∩ B) / p(A)

Where:

Therefore, To calculate the value of p(B/A), you need to know the probabilities of A and B, as well as the probability that both occur together.

Learn more about probability from

https://brainly.com/question/24756209

#SPJ1

Answer:

To mathematically prove that Marc hit the ball near the top of the tower, he could use the equation h(x) = -16x^2 + 120x, where h is the height of the ball and x is the number of seconds the ball is in the air.

First, Marc would need to determine the maximum height the ball reached during its flight. This can be found by using the vertex formula, which is x = -b/2a. In this case, a = -16 and b = 120, so x = -120/(2*-16) = 3.75 seconds.

Next, Marc can substitute this value back into the original equation to find the maximum height the ball reached. h(3.75) = -16(3.75)^2 + 120(3.75) = 135 feet.

Since the tower is 300 feet tall, Marc could conclude that if the ball hit near the top of the tower, it would have reached a height close to 300 feet. Since the ball reached a maximum height of 135 feet, it is unlikely that it hit the top of the tower.

However, this calculation assumes that the tower is directly in line with Marc's shot and that the ball did not have any horizontal movement. In reality, the tower could have been to the left or right of the shot, and the ball could have had some horizontal movement, which would affect its height at impact. Therefore, this calculation can only provide a rough estimate and cannot definitively prove whether or not the ball hit near the top of the tower.

The equation of the circle with center (3,6) and tangent to the x-axis is (x - 3)² + 36 = r²

In mathematics, a tangent is a straight line that touches a curve or surface at a single point and is perpendicular to the radius or line that passes through that point. The point of contact between the tangent and the curve or surface is called the point of tangency.

In geometry, the tangent to a circle is a straight line that intersects the circle at exactly one point. This point is called the point of tangency, and the tangent is perpendicular to the radius of the circle at that point.

The tangent is an important concept in calculus, where it is used to define the derivative of a function. The derivative of a function f(x) at a point x=a is defined as the slope of the tangent line to the graph of f(x) at the point (a, f(a)). This slope measures the rate at which the function is changing at that point.

If an equation is tangent to the x-axis, this means that it only intersects the x-axis at one point, which has a y-coordinate of zero. So, we need to write an equation of a circle with center (3,6) that intersects the x-axis at one point with a y-coordinate of zero.

Let the radius of the circle be r. Since the center of the circle is (3,6), the equation of the circle can be written in the form:

(x - 3)² + (y - 6)² = r²

Since the circle is tangent to the x-axis, we know that it intersects the x-axis at (x,0), where x is a point on the x-axis. Substituting y=0, we get:

(x - 3)² + (0 - 6)² = r²

Simplifying this equation, we get:

(x - 3)² + 36 = r²

So, the equation of the circle with center (3,6) and tangent to the x-axis is:

(x - 3)² + 36 = r²

Note that there are many possible values for r that would satisfy this equation, since we haven't specified the size of the circle. We only know that it is tangent to the x-axis and has center (3,6).

To know more about equation visit:

https://brainly.com/question/28994024

#SPJ1

The complete question is :

How do you write an equation with center (3,6), tangent to the x-axis?

Answer:

Axis of symmetry =1

vertex =(1,2)

y intercept =0

min/max= -6,2

domain= 0,1,2

range =y≥1,2

Answer:

3 and -16

Step-by-step explanation:

To find two numbers that add up to 13 but multiply to -48, we can start by making a list of the factors of -48:

1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 8, -8, 12, -12, 16, -16, 24, -24, 48, -48

We can see that the only two numbers in this list whose sum is 13 are 3 and -16. To verify that these numbers multiply to -48, we can simply multiply them together:

3 x (-16) = -48

Therefore, the two numbers that add up to 13 but multiply to -48 are 3 and -16.

Answer: -3, 16

Step-by-step explanation:

The solution to the system of equations using matrices is x = 45, y = 15, and z = 30.

A scalar value that can be calculated from a matrix's elements is the determinant. When a square matrix is used to transform vectors, the determinant is a measurement of how much the matrix "stretches" or "shrinks" space. In linear algebra, the determinant is employed in a variety of operations, including as the computation of a matrix's inverse, the description of a matrix's eigenvalues and eigenvectors, and the resolution of linear equation systems. In specifically, the existence of a unique solution, the absence of a solution, or an unlimited number of solutions to a system of linear equations can be determined using the determinant of the coefficient matrix.

The given equation are:

2x -y + 3z = 180

-4x + 2y + 3z = 225

3x - 4y = 270

Writing the equations in matrix form we have:

[tex]\begin{bmatrix} 2 & -1 & 3 \\ -4 & 2 & 3 \\ 3 & -4 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 180 \\ 225 \\ 270 \end{bmatrix}[/tex]

Multiplying the inverse of the coefficient matrix we have:

[tex]\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 2 & -1 & 3 \\ -4 & 2 & 3 \\ 3 & -4 & 0 \end{bmatrix}^{-1} \begin{bmatrix} 180 \\ 225 \\ 270 \end{bmatrix}[/tex]

Now,

[tex]\begin{bmatrix} 2/23 & 5/46 & -3/23 \\ 2/23 & 1/23 & 5/23 \\ -3/23 & -5/46 & 2/23 \end{bmatrix}[/tex]

Multiplying this by the vector on the right-hand side gives:

[tex]\begin{bmatrix} x \ y \ z \end{bmatrix} = \begin{bmatrix} 2/23 & 5/46 & -3/23 \\ 2/23 & 1/23 & 5/23 \\ -3/23 & -5/46 & 2/23 \end{bmatrix} \begin{bmatrix} 180 \\ 225 \\ 270 \end{bmatrix} = \begin{bmatrix} 45 \\ 15 \\ 30 \end{bmatrix}[/tex]

Hence, the solution to the system of equations is x = 45, y = 15, and z = 30.

Learn more about matrix here:

https://brainly.com/question/29132693

#SPJ1

The equation of the plane that passes through the line of intersection of x - z = 3 and y + 3z = 3 and is perpendicular to x + y - 4z = 6 is x + y - 4z = 3.

The point-normal form of the equation of a plane is given by:

N · (<x - x0>, <y - y0>, <z - z0>) = 0

Where (x0, y0, z0) is a point on the plane and N = is a normal vector to the plane, we have the point-normal form of the equation of a plane. The dot product of the vector from the supplied location to any point on the plane with the normal vector to the plane yields this form of the equation. The equation states that any vector located in the plane with the normal vector has a zero dot product. The scalar equation of the plane can also be found by expanding the dot product, and it takes the form axe + by + cz = d, where d = N (x0, y0, z0).

Given the equation of the planes is x − z = 3 and y + 3z = 3.

Now, find the direction vector of the line of intersection:

Set z = t:

x = t + 3 and y = 3 - 3t

The direction vector is <1, -3, 1>.

2. Determine the normal vector:

The plane is perpendicular to the plane x + y - 4z = 6, so:

normal vector of x + y - 4z = 6, which is <1, 1, -4>.

3. Using point normal form we have:

(3, 0, 0)

The point satisfies the equation:

x - z = 3 and y + 3z = 3 when z = 0

Thus,

<1, 1, -4> · <x - 3, y, z> = 0

x + y - 4z = 3

Hence, the equation of the plane that passes through the line of intersection of x - z = 3 and y + 3z = 3 and is perpendicular to x + y - 4z = 6 is x + y - 4z = 3.

Learn more about equation of plane form:

https://brainly.com/question/14695894

#SPJ1

Answer: less than

Step-by-step explanation: