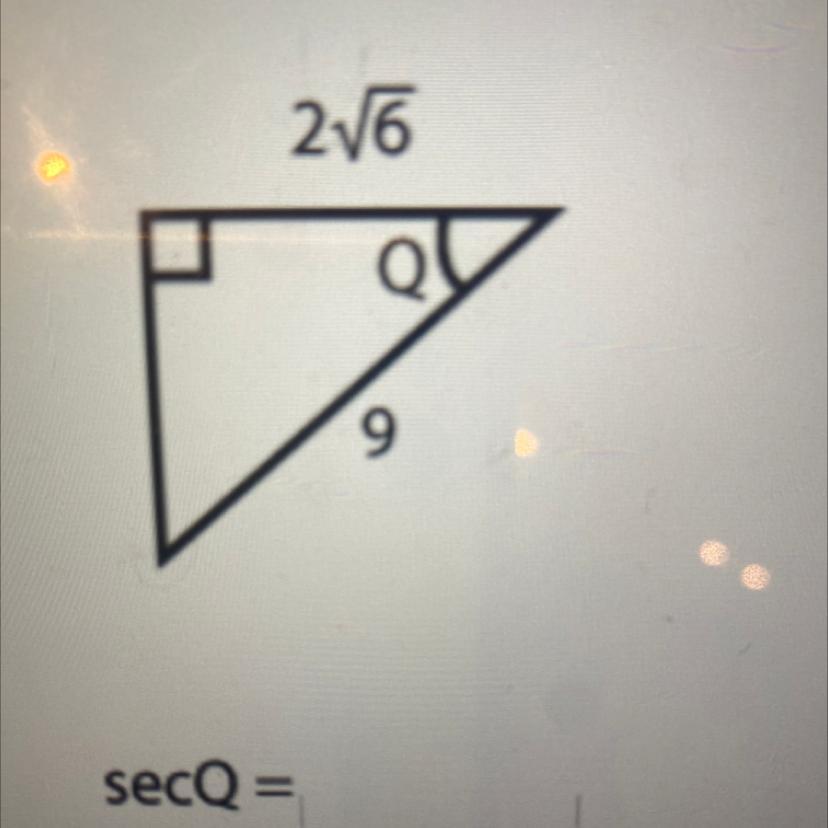
Answers
Answer: the simplified form of sec(Q) is sqrt(24/7).
Step-by-step explanation: The equation secant of angle Q is equal to two multiplied by the square root of six and divided by nine.
In order to reduce the complexity of the given mathematical expression, it is possible to employ the fundamental definition of secant, which states that:
The trigonometric identity denoted as sec(Q) equals the reciprocal of the cosine function evaluated at the angle Q. More precisely, sec(Q) = 1 / cos(Q).
The value of cos(Q) may be determined through the utilization of the Pythagorean identity.
The present mathematical equation demonstrates a fundamental identity in trigonometry, wherein the squares of the sine and cosine functions are summed to equal one. Written symbolically, the equation can be expressed as sin^2(Q) + cos^2(Q) = 1.
Given the condition that sec(Q) is positive, it is ascertainable that Q is situated within the first or fourth quadrant, wherein the cosine of Q is likewise positive. Consequently, the derivation for the solution of the cosine of the angle Q can be expressed as follows:
The trigonometric identity expressed as cos(Q) = sqrt(1 - sin^2(Q)) is a fundamental result in the field of mathematics. This particular equation provides a relationship between the cosine and sine functions of angle Q. Specifically, it states that the cosine of an angle Q is equal to the square root of one minus the sine squared of the same angle Q. The use of such identities is common in mathematical analysis and applied sciences, where it allows for efficient manipulation of trigonometric functions and the mathematical modeling of a variety of physical phenomena.
The following mathematical expression can be written in an academic style: Cosine of angle Q can be expressed as the square root of one minus the square of nine divided by twice the square root of six, i.e., cos(Q) = √(1 - (9/2√6)^2), while substituting the value of sine of angle Q as being equal to nine divided by twice the square root of six (i.e., sin(Q) = 9/2√6).
The mathematical expression cos(Q) = sqrt(1 - (81/24)) may be represented in a more academic manner. Specifically, it may be articulated as follows: the cosine of angle Q is equivalent to the square root of one subtracted by the quotient of 81 and 24. This revision lends itself to a more formal and precise mode of communication, which is characteristic of academic writing.
The mathematical expression cos(Q) = √(7/24) can be represented in a formal and academic manner.
The value of secant of angle Q can now be determined as:
The trigonometric function defining the secant of an angle Q is expressed as sec(Q) = 1/cos(Q).
The trigonometric function, sec(Q), can be expressed as the reciprocal of the square root of 7/24.
The mathematical statement, sec(Q) = sqrt(24/7), can be expressed in a formal and academic manner as follows. The reciprocal of the cosine function of the angle Q is equivalent to the square root of the fraction 24 over 7.
Related Questions
In ΔHIJ, i = 550 inches, h = 460 inches and ∠H=159°. Find all possible values of ∠I, to the nearest degree.
Answers
c^2 = a^2 + b^2 - 2ab cos(A)
In this case, we know the lengths of sides HI and HJ, and the measure of angle H. We want to find the measure of angle I, so we will use the Law of Cosines to solve for side HJ:
HJ^2 = HI^2 + HJ^2 - 2(HI)(HJ)cos(∠I)
Simplifying this equation, we get:
2(HI)(HJ)cos(∠I) = HI^2 + HJ^2 - HJ^2
2(HI)(HJ)cos(∠I) = HI^2
cos(∠I) = HI^2 / 2(HI)(HJ)
cos(∠I) = HI / 2(HJ)
cos(∠I) = 460 / (2 * 550)
cos(∠I) = 0.41818181818181815
Now, we can use the inverse cosine function (cos^-1) to find the possible values of ∠I:
∠I = cos^-1(0.41818181818181815)
∠I ≈ 65.6°
Note that the Law of Cosines can give two possible values for an angle in a triangle, but in this case, we only get one valid value since the given angle H is obtuse (greater than 90°) and the other possible angle value obtained by the Law of Cosines would be greater than 180°, which is not possible. Therefore, the only possible value of ∠I in this triangle is approximately 65.6° to the nearest degree.
A diamond merchant received a shipment of 7/10 of a pound of diamonds. He divided the diamonds into 7 equal lots and sold them to jewelers for making rings and necklaces. What was the weight of the diamonds in each lot?
Write your answer as a fraction or as a whole or mixed number.
Answers
The weight of the diamonds in each lot was 1/10 of a pound, or 0.1 pound.
What is arithmetic sequence?
An arithmetic sequence is a sequence of numbers in which each term after the first is found by adding a fixed constant number, called the common difference, to the preceding term. For example, the sequence 2, 5, 8, 11, 14, ... is an arithmetic sequence with a common difference of 3, since each term after the first is found by adding 3 to the preceding term.
The nth term of an arithmetic sequence can be found using the formula:
an = a1 + (n-1)d.
The merchant received 7/10 of a pound of diamonds and divided them into 7 equal lots. To find the weight of each lot, we need to divide 7/10 by 7:
(7/10) ÷ 7 = (7/10) × (1/7) = 1/10
Therefore, the weight of the diamonds in each lot was 1/10 of a pound, or 0.1 pound.
To learn more about arithmetic sequence from the given link:
https://brainly.com/question/15412619
#SPJ1
Find the Taylor Polynomial 3P x (up to3
x ) for( ) x
f x e , centered at0x ?
Answers
We have to find the Taylor Polynomial of $f(x)=e^x$ up to the third degree, centered at $x=0$.
The Taylor Polynomial is given by:
(x)=∑
k=0
n
k!
f
(k)
(a)
(x−a)
k
where $f^{(k)}(a)$ is the $k$th derivative of $f(x)$ evaluated at $a$.
Using this formula, we can find the Taylor Polynomial as follows:
\begin{align*}
f(x) &= e^x \
f'(x) &= e^x \
f''(x) &= e^x \
f'''(x) &= e^x \
\end{align*}
Evaluating each derivative at $x=0$, we get:
\begin{align*}
f(0) &= e^0 = 1 \
f'(0) &= e^0 = 1 \
f''(0) &= e^0 = 1 \
f'''(0) &= e^0 = 1 \
\end{align*}
Substituting these values into the formula for the Taylor Polynomial, we get:
\begin{align*}
P_3(x) &= \frac{f(0)}{0!}(x-0)^0 + \frac{f'(0)}{1!}(x-0)^1 + \frac{f''(0)}{2!}(x-0)^2 + \frac{f'''(0)}{3!}(x-0)^3 \
&= 1 + x + \frac{x^2}{2} + \frac{x^3}{6}
\end{align*}
Therefore, the Taylor Polynomial of $f(x)=e^x$ up to the third degree, centered at $x=0$, is $P_3(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6}$.
The first three terms of a sequence are given. Round to the nearest thousandth (if necessary). 12 , 18 , 27 , . . . Find the 8th term.
Answers
Answer: 205.031(nearest thousandth)
or 205.03125
Step-by-step explanation:
In the first 5 years of the 1940s, how many acres expanded for wheat production
in the Great Plains? How did much more was the land being sold for?
Answers
The exact acreage of wheat expansion during the first 5 years of the 1940s would require access to historical data .Land prices increased significantly due to the high demand for wheat and the increased production.
Which regions are included in Great Plains?The Great Plains region includes parts of the United States and Canada, specifically the central and western portions of North America. In the United States, it includes parts of Montana, North Dakota, South Dakota, Nebraska, Kansas, Oklahoma, Texas, Colorado, Wyoming, and New Mexico. In Canada, it includes parts of Alberta, Saskatchewan, and Manitoba.
During the 1940s, the Great Plains region of the United States, which includes states such as Kansas, Nebraska, Oklahoma, and parts of other surrounding states, experienced a significant expansion in wheat production. This period is often referred to as the "wheat boom" era.
During the early 1940s, there was a high demand for wheat due to World War II, as wheat was a staple crop used to feed soldiers and provide food aid to war-torn regions. This resulted in increased wheat production in the Great Plains region. However, the exact acreage of wheat expansion during the first 5 years of the 1940s would require access to historical data .
As for the prices of land being sold during that time, it is also difficult to provide precise information without specific data. Land prices can vary depending on various factors such as location, quality of land, demand, and economic conditions. However, it is generally known that during the wheat boom era of the 1940s, land prices in the Great Plains region increased significantly due to the high demand for wheat and the increased production. The exact percentage of increase would require access to historical data and research.
Learn more about Great Plains here:
https://brainly.com/question/30318044
#SPJ1
Pedro wants to grow tomatoes and herbs so he can make his own fresh pizza sauce. Pedro's planter box is seven feet long and four feet wide on the inside. Pedro fills the planter box with soil to a height of two feet. What is the volume of soil in Pedro's planter box?
Answers
According to the question the volume of soil in Pedro's planter box is 56 cubic feet (ft³).
What is volume?Volume is a measure of the amount of space that a three-dimensional object occupies or contains. It is measured in units of cubic centimeters (cm3), cubic meters (m3) or liters. Volume is an important concept in many areas of mathematics, including geometry, calculus and physics. It is also a key concept in many other disciplines, including engineering, architecture and the sciences. Volume is an important property of a solid object, and it is often used to quantify the size or capacity of an object. Volume can be calculated by multiplying the length, width and height of an object. It can also be calculated using the formula for the volume of a cylinder, cone, sphere or other shapes.
To calculate this, we need to multiply the length of the planter box (7 ft) by the width (4 ft) by the height of the soil (2 ft). This gives us the following equation: 7 ft x 4 ft x 2 ft
= 56 ft³.
To learn more about volume
https://brainly.com/question/1972490
#SPJ1
the 3rd and 6th term in fibonacci sequence are 7 and 31 respectively find the 1st and 2nd terms of the sequence
Answers
Answer:
7 and 31 it asks
the 3rd and 6th is
The 1st and 2nd terms of this Fibonacci sequence, given the 3rd and 6th terms would be 2 and 5.
How to find the Fibonacci sequence terms ?Let's denote the first and second terms of the Fibonacci sequence as F1 and F2. The Fibonacci sequence is defined by the recurrence relation:
F(n) = F(n-1) + F(n-2)
We are given that the 3rd term (F3) is 7 and the 6th term (F6) is 31. We can use this information to set up the following equations:
F3 = F2 + F1 = 7
F6 = F5 + F4 = 31
We can also express F4 and F5 in terms of F1 and F2:
F4 = F3 + F2 = (F2 + F1) + F2 = F1 + 2F2
F5 = F4 + F3 = (F1 + 2F2) + (F2 + F1) = 2F1 + 3F2
Now, let's substitute equation (4) into equation (2):
F6 = 2F1 + 3F2 + F1 + 2F2 = 31
3F1 + 5F2 = 31
By trial and error, we can find the possible values for F1 and F2 that satisfy this equation:
F1 = 1, F2 = 6: 3(1) + 5(6) = 3 + 30 = 33 (not a solution)
F1 = 2, F2 = 5: 3(2) + 5(5) = 6 + 25 = 31 (solution)
The solution is F1 = 2 and F2 = 5, so the first two terms of the Fibonacci sequence are 2 and 5.
Find out more on Fibonacci sequence at https://brainly.com/question/29764204
#SPJ1
There is a sale at khols, and tennis shoes are 30% off. How much are you saving if the shoes originally cost $62
Answers
Answer: $18.6
Step-by-step explanation: If we take a look at the sale off the shoes cost which is $43.4 and look at the sale amount (30%) which is 18 dollars and 60 cents the answer is: 18.6 or $18.6 off
Classify the following polynomial by its degree and the number of terms:
9x 3+4x 2 −7
Answers
We can classify the polynomial as a "trinomial" with a degree of 3.
How to Classify the following polynomial by its degreeThe given polynomial is:
9x^3 + 4x^2 - 7
The degree of a polynomial is the highest power of the variable present in the polynomial. In this case, the degree of the polynomial is 3, because the highest power of x in the polynomial is 3.
The number of terms in a polynomial is the number of individual expressions added or subtracted together. In this case, the polynomial has three terms: 9x^3, 4x^2, and -7.
Therefore, we can classify the polynomial as a "trinomial" with a degree of 3.
Learn more about polynomial at https://brainly.com/question/2833285
#SPJ1
The area of a figure in the shape of a
parallelogram is 74.4 m2 . If the height of
the parallelogram is 6 m, then what is the
length?
Answers
The area of a figure in the shape of a parallelogram is 74.4 m2 . If the height of the parallelogram is 6 m, the length of the parallelogram is 12.4 meters.
Describe Parallelogram?A parallelogram is a four-sided plane figure with opposite sides parallel and equal in length. It is a special type of quadrilateral, which is a polygon with four sides.
The opposite sides of a parallelogram are parallel, which means they have the same slope and never intersect. The opposite sides are also equal in length, which means they have the same distance between them.
The adjacent angles of a parallelogram are supplementary, which means they add up to 180 degrees. This property is known as the parallelogram law, which states that the sum of the squares of the diagonals of a parallelogram equals the sum of the squares of its sides.
The area of a parallelogram can be calculated by multiplying the base by the height. The base is one of the parallel sides, and the height is the perpendicular distance between the base and the opposite side.
The area (A) of a parallelogram is given by the formula:
A = base x height
where the base is the length of one of the sides of the parallelogram and the height is the perpendicular distance between the base and the opposite side.
In this problem, we are given the area of the parallelogram as 74.4 m² and the height as 6 m. Let the length of the parallelogram be denoted by b. Then, we can use the formula for the area of a parallelogram to write:
74.4 m² = b x 6 m
Solving for b, we get:
b = 74.4 m² / 6 m
b = 12.4 m
Therefore, the length of the parallelogram is 12.4 meters.
To know more about height visit:
https://brainly.com/question/872767
#SPJ1
i don't understand this question please help me answer it :)
Answers
If $r=9$ and $4r+3s=75$, what is the value of $s$? asap answer i only have like 1 hour to answer 50 questions
Answers
Answer:
the value of $s$ is 13.
Step-by-step explanation:
We are given that $r=9$ and $4r+3s=75$. We can use the value of $r$ to find $s$.
Substituting $r=9$ into the second equation, we get:
$4(9) + 3s = 75$
Simplifying the left-hand side, we get:
$36 + 3s = 75$
Subtracting 36 from both sides, we get:
$3s = 39$
Dividing both sides by 3, we get:
$s = 13$
Therefore, the value of $s$ is 13.
Jackson has a loyalty card good for a 10% discount at his local hardware store. What would his total in dollars and cents be, after the discount and before tax, if the total cost of all the items he wants to buy is $27.40? Round to the nearest cent.
Answers
Jackson's total cost after the discount and before tax would be $24.67.
Calculating discounted price :When a store offers a discount, it reduces the price of the item by a certain percentage. In this case, Jackson has a loyalty card that gives him a 10% discount on his purchase.
To calculate the price after the discount, we multiply the original price by 1 minus the discount percentage (in decimal form).
Here we have
Jackson has a 10% discount at his local hardware store.
Let 'x' be the cost before tax
After a 10% discount,
The amount that Jackson could pay 90% of the cost
Given that he wants to buy $ 27.40
The cost of items after discount = 90% of 27.40
= [ 90/100 ] × 27.40
= [ 0.9 ] × 27.40
= 24.66
Therefore,
Jackson's total cost after the discount and before tax would be $24.67.
Learn more about Discounts at
https://brainly.com/question/30814332
#SPJ9
answer these questions in detail
Answers
Answer:
5. x = 60
6. F' (1, 4)
Step-by-step explanation:
5. The angles shown are same side exterior angles, so they are supplementary (add to 180)
(x + 85) + 35 = 180
x + 120 = 180
x = 180 - 120 = 60
x = 60
6. The line x = 1 is a vertical line, passing through the x=axis at (1, 0). All x coordinates on this line equal 1.
The point F (3,4) is reflected in the line x = 1 at the point F' (1, 4)
the perimeter of rectangle is 76m if one side is 16m what is the other side?
Answers
The formula for the perimeter of a rectangle is:
P = 2(l + w)
where P is the perimeter, l is the length, and w is the width.
We know that the perimeter of the rectangle is 76m, so we can substitute the values in the formula:
76 = 2(16 + w)
Simplifying the equation:
76 = 32 + 2w
Subtracting 32 from both sides:
44 = 2w
Dividing both sides by 2:
w = 22
Therefore, the width of the rectangle is 22 meters.
Answer: 22
Step-by-step explanation:
The formula for perimeter of a rectangle is side 1 + side 1 + side 2 + side 2. Side one is 16. This means that 16x2 is 32. Then, you realize there are 44 meters remaining. 44/2=22. The other side is 22.
A survey was conducted one month ago to review the calories of lunch boxes provided by the supplier "Better
Lunch". In a sample with 300 lunch boxes, there were 273 lunch boxes with calories below 650 and the other
27 lunch boxes with calories above 650. Besides, the mean calories was 550 and standard deviation was 40.
(a) Find the point estimate of the population proportion of lunch boxes provided by "Better Lunch" had
calories above 650.
(b) Calculate the sampling error at 98% confidence level for the estimate of the population proportion of
lunch boxes provided by "Better Lunch" had calories above 650.
(c) Construct a 98% confidence interval estimate of the population proportion of lunch boxes provided by
"Better Lunch" had calories above 650.
(d) "Better Lunch" follows government's suggestions to change the menu in order to reduce the lunch boxes'
calories. Suppose after the menu update, each lunch box's calories can be reduced by 4%. Find the
sample mean and sample standard deviation of calories of the above sample after the change. Hence,
construct a 90% confidence interval estimate of the population mean calories in a lunch box after the
change.
Answers
The answers to both the subparts using the confidence interval are shown:
(A) His population's mean finishing time for the 100-meter event has a 99% confidence interval of (12.8081,15.5919).
(B) The right choice is Option B, which is Option II which is narrower.
What is a confidence interval?The mean of your estimate plus and minus the range of that estimate constitutes a confidence interval.
Within a specific level of confidence, this is the range of values you anticipate your estimate to fall within if you repeat the test.
The 95% confidence level is the most popular, however other levels, such as 90% or 99%, are occasionally used when computing confidence intervals.
So, let X represent the amount of time (in seconds) needed to complete a 100-meter race with Tom.
His population's mean 100-meter race finishing time falls within a 99% confidence interval of 12.8081 and 15.5919.
x = 14.2
s²= 0.9867
s= 0.9933
t α2, n-1 = 3.7074
The margin of error= 1.3919
lower bound= 12.8081
upper bound= 15.5919
Therefore, the answers to both the subparts using the confidence interval are shown:
(A) His population's mean finishing time for the 100-meter event has a 99% confidence interval of (12.8081,15.5919).
(B) The right choice is Option B, which is Option II which is narrower.
Know more about the confidence interval here:
https://brainly.com/question/15712887
#SPJ1
Correct question:
Tom is preparing for a 100 meters race competition. During his practice last week, a sample of seven 100
meters races is reviewed, and the finishing times (in seconds) were as below:
13.4
15.6
13.1
14.5
14.2
13.3
15.3
It is reasonable to assume his finishing times are normally distributed.
(a) Construct a 99% confidence interval estimate of his population mean finishing time of 100 meters race.
(b) If the confidence interval estimate of his population mean finishing time of 100 meters is constructed at 95% instead of 99%, would the new confidence interval be (I) wider, (II) narrower, or (III) the same as the interval constructed at part (a)? (Just state your answer, no calculation is needed in part (b))
721.60 divided by 80
Answers
hope this helps !!
Explain Why 387 is not a term of the sequence
Answers
Answer:
In order to determine whether 387 is a term of a sequence, we need to know the rule or formula for generating the sequence. Without this information, it is not possible to determine whether 387 is a term of the sequence or not.
If we assume that the sequence is an arithmetic sequence, where each term is obtained by adding a fixed constant to the previous term, we can use the following formula to determine whether 387 is a term of the sequence:
an = a1 + (n-1)d
where a1 is the first term of the sequence, d is the common difference between consecutive terms, and n is the term we are trying to find.
If we substitute the values for the first few terms of the sequence, we can check whether 387 is a term or not. For example, if the first few terms of the sequence are:
a1 = 3
a2 = 8
a3 = 13
a4 = 18
and so on, with a common difference of 5 between consecutive terms, we can use the formula to find the value of the 129th term of the sequence:
a129 = a1 + (129-1)d
a129 = 3 + 128(5)
a129 = 643
Since 387 is not equal to 643, it is not a term of this sequence. However, without knowing the rule or formula for generating the sequence, it is impossible to say for certain whether 387 is a term or not.
Much help would be greatly needed!
For a $85,000 mortgage, the borrower was charged the following closing costs.
Loan origination fee (1% of mortgage) $
Broker loan fee $1640
Lender document and underwriting fees $350
Lender tax and wire fees $210
Fee to title company $225
Title insurance fee $320
Title reconveyance fee $70
Document recording fee $40
Compute the total closing costs for this mortgage:
Answers
Answer:
hope this helps
Step-by-step explanation:
The total closing costs for this mortgage can be calculated as follows:
Loan origination fee: 1% of $85,000 = $850
Broker loan fee: $1,640
Lender document and underwriting fees: $350
Lender tax and wire fees: $210
Fee to title company: $225
Title insurance fee: $320
Title reconveyance fee: $70
Document recording fee: $40Total closing costs = $850 + $1,640 + $350 + $210 + $225 + $320 + $70 + $40
Total closing costs = $3,705
Therefore, the total closing costs for this mortgage are $3,705.
Leon is building a square picture frame. The side of the frame is 335 millimeters long. If a meter of wood costs $8, how much will the wood he needs cost?
Answers
Answer: $9.66
Step-by-step explanation: perimeter = 345mm + 345mm + 345mm + 345mm = 1380
We need 1380 millimeters which is equivalent to 1.38 meters.
We can multiply the number of meters by the cost of meters to find the total
If $20,000 is invested at an interest rate of 2% per year, compounded semiannually, find the value of the investment after the given number of years. (Round your answers to the nearest cent.)
6 years
12 years
18 years
Answers
Answer:
6 years = $22,536.50
12 years = $25,394.69
18 years = $28,615.38
Step-by-step explanation:
The find the value of the investment after the given number of years, first create an equation for A in terms of t using the compound interest formula.
Compound Interest Formula[tex]\boxed{\sf A=P\left(1+\frac{r}{n}\right)^{nt}}[/tex]
where:
A = Final amount.P = Principal investment.r = Interest rate (in decimal form).n = Number of times interest is applied per year.t = Time (in years).Given values:
P = $20,000r = 2% = 0.02n = 2 (semi-annually)Substitute the given values into the formula to create an equation for the value of the investment, A, in terms of time in years, t:
[tex]\implies \sf A=20000\left(1+\dfrac{0.02}{2}\right)^{2t}[/tex]
[tex]\implies \sf A=20000\left(1+0.01\right)^{2t}[/tex]
[tex]\implies \sf A=20000\left(1.01\right)^{2t}[/tex]
[tex]\hrulefill[/tex]
To find the value of the investment after 6 years, substitute t = 6 into the equation:
[tex]\implies \sf A=20000\left(1.01\right)^{2\cdot 6}[/tex]
[tex]\implies \sf A=20000\left(1.01\right)^{12}[/tex]
[tex]\implies \sf A=20000(1.12682503...)[/tex]
[tex]\implies \sf A=22536.5006026...[/tex]
Therefore, the value of the investment after 6 years is $22,536.50 rounded to the nearest cent.
[tex]\hrulefill[/tex]
To find the value of the investment after 12 years, substitute t = 12 into the equation:
[tex]\implies \sf A=20000\left(1.01\right)^{2 \cdot 12}[/tex]
[tex]\implies \sf A=20000\left(1.01\right)^{24}[/tex]
[tex]\implies \sf A=20000\left(1.2697346...\right)[/tex]
[tex]\implies \sf A=25394.69297...[/tex]
Therefore, the value of the investment after 12 years is $25,394.69 rounded to the nearest cent.
[tex]\hrulefill[/tex]
To find the value of the investment after 18 years, substitute t = 18 into the equation:
[tex]\implies \sf A=20000\left(1.01\right)^{2\cdot 18}[/tex]
[tex]\implies \sf A=20000\left(1.01\right)^{36}[/tex]
[tex]\implies \sf A=20000\left(1.43076878...\right)[/tex]
[tex]\implies \sf A=28615.37567...[/tex]
Therefore, the value of the investment after 18 years is $28,615.38 rounded to the nearest cent.
Suppose Fatima went to buy a $25,000 car and wanted to own it after 5 years. If she got a
4.7% interest rate, what is her monthly payment?
Answers
Therefore, Fatima's monthly payment would be $460.23.
What is interest?Interest is the amount of money that is charged by a lender to a borrower for the use of money or a loan. It is usually calculated as a percentage of the principal amount (the amount of money borrowed) and can be either simple or compound, depending on the type of loan. Interest is typically paid by the borrower to the lender over a set period of time, such as monthly, quarterly, or annually. The interest rate can be fixed or variable, and is determined by a variety of factors including the borrower's creditworthiness, the amount of the loan, and the length of the repayment period.
Here,
To calculate the monthly payment for a car loan, we need to use the formula:
M = P [ i(1 + i)ⁿ] / [ (1 + i)ⁿ – 1]
Where:
M = monthly payment
P = principal (the amount of the loan)
i = monthly interest rate (annual interest rate divided by 12)
n = number of months
First, we need to calculate the monthly interest rate:
i = 4.7% / 12
= 0.003917
Next, we need to calculate the number of months:
n = 5 years x 12 months/year
= 60 months
Now, we can plug in the values and solve for M:
M = 25,000 [ 0.003917(1 + 0.003917)⁶⁰ ] / [ (1 + 0.003917)⁶⁰ – 1]
M = $460.23 (rounded to the nearest cent)
To know more about interest,
https://brainly.com/question/28792777
#SPJ1
Janna's health class measures the heart rates of students after they walked for five minutes. The heart rates, in beats
per minute, were as follows.
102, 74, 86, 74, 96, 95, 103, 102 Find the median of the data set. What does the median tell you? (Hint: If the data set has an even number of values,
the median is the mean of the two middle values.)
Answers
The median of the data set is: 95.5
What is median?
median is the number at the middle of the given data.
To find the median of the data set {102, 74, 86, 74, 96, 95, 103, 102}, we first need to arrange the values in order from lowest to highest:
74, 74, 86, 95, 96, 102, 102, 103
Since the data set has an even number of values, the median is the mean of the two middle values. In this case, the two middle values are 95 and 96.
Therefore, the median of the data set is: (95 + 96) / 2 = 95.5
To know more about median visit,
https://brainly.com/question/26177250
#SPJ1
What is 8% of 425 coins?
Answers
Answer: 34
Step-by-step explanation:
To find 8% of 425 coins, multiply 425 by 0.08 (which is the decimal equivalent of 8%).
425 * 0.08 = 34
So, 8% of 425 coins is 34 coins.
425 x 0.08= 34
HELP ME PLS THIS IS A SCREENSHOT I WILL ADD MORE PONINTS
Answers
Answer:
Estimated difference: 88 - 6 = 82
Actual difference: 87.71 - 5.8 = 81.91
Use the image to determine the line of reflection.
An image of polygon VWYZ with vertices V at negative 7, negative 2, W at negative 7, negative 4, Y at negative 1, negative 4, and Z at negative 1, negative 2. A second polygon V prime W prime Y prime Z prime with vertices V prime at 11, negative 2, W prime at 11, negative 4, Y prime at 5, negative 4, and Z prime at 5, negative 2.
Reflection across the x-axis
Reflection across the y-axis
Reflection across y = −2
Reflection across x = 2
Answers
An image of polygon VWYZ has a line of reflection across the x-axis. So option A is correct.
What is the line of reflection?In geometry, the line of reflection is the line over which a figure is reflected. When a point is reflected over a line, it moves the same distance on the opposite side of the line. The line of reflection is perpendicular to the figure at the point of reflection and is equidistant from the figure and its reflection.
What is a polygon?A polygon is a closed two-dimensional shape with straight sides. The sides are line segments that intersect only at their endpoints, called vertices. Polygons can have any number of sides, but they must have at least three. Common examples of polygons include triangles, squares, rectangles, pentagons, hexagons, and octagons.
What is the formula for the line of reflection?The formula for the line of reflection in a Cartesian coordinate system is:
x = a
where a is the equation of the line of reflection.
This formula represents a vertical line that passes through the point (a, 0) and reflects points across the line of reflection to their corresponding images on the other side.
To know more about the line of reflection visit:
brainly.com/question/29248743
#SPJ1
Answer:
reflection across x=2
Step-by-step explanation:
the picture should be able to explain itself! :)))
differentiate x^5(2x+1)^5
Answers
Answer:
[tex]5x^4(2x+1)^4(4x+1)[/tex]
Step-by-step explanation:
Okay so we have to use the product rule for this i.e.
d/dx[uv] = u'v + uv'
d/dx[x^5(2x+1)^5] =
[tex]5x^4(2x+1)^5 + x^5 * 2 * 5(2x+1)^4\\\\= 5x^4(2x+1)^5 + 10x^5(2x+1)^4\\\\= (2x+1)^4[5x^4(2x+1) + 10x^5]\\\\= (2x+1)^4[10x^5 + 5x^4 + 10x^5]\\\\= (2x+1)^4(20x^5+5x^4)\\\\=5x^4(2x+1)^4(4x+1)[/tex]
Hope this helps and be sure to mark this as brainliest! :)
Let g(x)=x^5+x^4. On which intervals is g decreasing
Answers
g(x) is decreasing function on the interval (-4/5, 0).
What is calculus?Calculus is a branch of mathematics that deals with the study of rates of change and the accumulation of small changes to find the overall effect. It provides a framework for modeling and analyzing a wide range of phenomena, from the motion of objects to the behavior of complex systems.
Calculus is divided into two main branches: differential calculus and integral calculus. Differential calculus deals with the study of rates of change, slopes of curves, and the computation of derivatives. Integral calculus deals with the study of accumulation of small changes, computation of areas, and the computation of integrals.
To determine where g(x) is decreasing, we need to find where its derivative is negative.
The derivative of g(x) is:
g'(x) = 5x⁴ + 4x³
To find where g'(x) < 0, we can factor out a common term of x³ to get:
g'(x) = x³(5x + 4)
So, g'(x) < 0 when:
x³ < 0 and 5x + 4 < 0
This condition is not possible, as x³ is never negative.
x³ > 0 and 5x + 4 < 0
This condition is satisfied when -4/5 < x < 0.
Therefore, g(x) is decreasing function on the interval (-4/5, 0).
To learn more about decreasing function from the given link
https://brainly.com/question/26111694
#SPJ1
What fractions are close to 1 than to 0
Answers
The answer of the given question based on the fraction is , a value that is greater than 1/2.
What is Fraction?A fraction is mathematical expression that represents part of whole or ratio between the two numbers. It is expressed in the form of a ratio of two integers, with a numerator and a denominator separated by a horizontal or slanted line called a fraction bar.
Fractions that are closer to 1 than to 0 have a value that is greater than 1/2. This is because 1/2 is exactly halfway between 0 and 1 on the number line.
So, any fraction that has a numerator greater than its denominator is closer to 1 than to 0. For example:
2/3 is closer to 1 than to 0 because it is greater than 1/2
7/8 is closer to 1 than to 0 because it is greater than 1/2
3/4 is closer to 1 than to 0 because it is greater than 1/2
On the other hand, fractions that have a value less than 1/2 are closer to 0 than to 1. For example:
1/4 is closer to 0 than to 1 because it is less than 1/2
3/10 is closer to 0 than to 1 because it is less than 1/2
2/5 is closer to 0 than to 1 because it is less than 1/2
To know more about Expression visit:
https://brainly.com/question/1859113
#SPJ1
The number of deer on an island is given by D=200+100sin( 2 π x), where x is the number of years since 2000. Which is the first year after 2000 that the number of deer reaches 150 ?
Answers
Therefore, the first Leap year after 2000 that the number of deer reaches 150 is 2000.1, or 2000 and 1/10 of a year.
What are a leap year and a year?If you sum up all the days on a calendar from January to December, there are 365 in a regular year. But about every four years, February has 29 days rather than 28. Therefore, a year has 366 days. There is a term for it: a leap year.
We must find x in the equation D=150 in order to determine the year that the number of deer exceeds 150 for the first time after 2000.
150=200+100sin(2πx)
Subtracting 200 from both sides, we get:
-50 = 100sin(2πx)
Dividing both sides by 100, we get:
-0.5 = sin(2πx)
To find the value of x that satisfies this equation, we can take the inverse sine of both sides:
sin⁻¹(-0.5) = 2πx
Using a calculator, we find that sin⁻¹(-0.5) = -π/6.
-π/6 = 2πx
Solving for x, we get:
x = -1/12
Since x is the number of years since 2000, we need to add 1/12 to find the first year after 2000 that the number of deer reaches 150:
2000 + 1/12 ≈ 2000.1
To know more about Leap year visit:-
https://brainly.com/question/24068575
#SPJ1