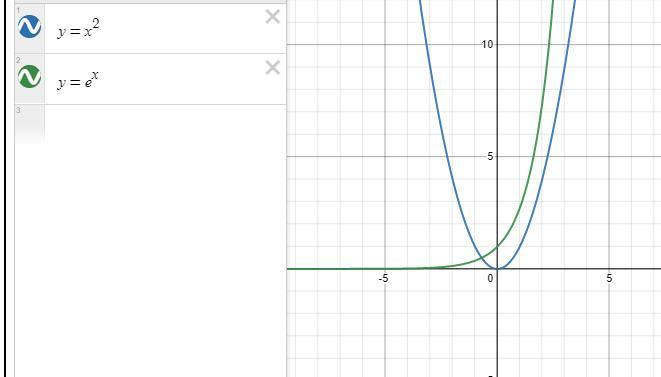
Sketch then find the area of the region bounded by the curves of each the elow pair of functions on the given intervals. 4. y=e*, y=x²,1 5x54
Answers
The total area of the regions between the curves is 30.88 square units
Calculating the total area of the regions between the curvesFrom the question, we have the following parameters that can be used in our computation:
y = eˣ and y = x²
The interval is given as
1 ≤ x ≤ 4
So, the area of the regions between the curves is
Area = ∫x² - eˣ dx
This gives
Area = ∫[x² - eˣ] dx
Integrate
Area = x³/3 - eˣ
Recall that 1 ≤ x ≤ 4
So, we have
Area = [1³/3 - e¹] - [4³/3 - e⁴]
Evaluate
Area = 30.88
Hence, the total area of the regions between the curves is 30.88 square units
The graph is attached
Read more about area at
brainly.com/question/15122151
#SPJ4
Related Questions
Christina's (122 lbs) maximal absolute oxygen consumption (VO2max) is 1.4 L/min. What is her relative VO2max in ml/kg/min? a) 2.58 ml/kg/min b) 25.2 ml/kg/min c) 38.6 ml/kg/min d) 18.6 mL/kg/min
Answers
The correct answer is option b) 25.2 ml/kg/min.The relative VO2max is a measure of maximal oxygen consumption adjusted for body weight. To calculate it, we need to convert Christina's weight from pounds to kilograms and then divide her absolute VO2max (in liters per minute) by her body weight in kilograms.
Given that Christina weighs 122 pounds, we can convert it to kilograms by dividing by 2.2046 (1 pound = 0.4536 kilograms). Therefore, her weight is approximately 55.45 kilograms.
Next, we divide her absolute VO2max of 1.4 L/min by her body weight of 55.45 kilograms. The result is approximately 0.0252 L/kg/min.
To convert liters to milliliters, we multiply by 1000. Therefore, Christina's relative VO2max is approximately 25.2 ml/kg/min.
Therefore, the correct answer is option b) 25.2 ml/kg/min.
To learn more about oxygen consumption : brainly.com/question/13959817
#SPJ11
Find the volume of the solid generated when the region enclosed by the curve y = 2 + sinx, and the z axis over the interval 0≤x≤ 2n is revolved about the x-axis. Make certain that you sketch the region. Use the disk method. Credit will not be given for any other method. Give an exact answer. Decimals are not acceptable.
Answers
The volume of the solid generated by revolving the region enclosed by the curve y = 2 + sinx and the z-axis over the interval 0 ≤ x ≤ 2π around the x-axis using the disk method is 16π cubic units.
To find the volume using the disk method, we divide the region into infinitesimally thin disks perpendicular to the x-axis and sum up their volumes. The curve y = 2 + sinx intersects the x-axis at x = 0 and x = 2π, enclosing a region. We need to find the volume of this region when revolved around the x-axis.
Since we are revolving the region about the x-axis, the radius of each disk is given by the y-coordinate of the curve, which is (2 + sinx). The area of each disk is πr², where r is the radius. Thus, the volume of each disk is πr²* dx.
Integrating this volume expression over the interval 0 ≤ x ≤ 2π will give us the total volume. Using the disk method, we can set up the integral as follows:
V = ∫(0 to 2π) π(2 + sinx)² dx.
Evaluating this integral will yield the volume of the solid. Simplifying the integral expression and performing the calculations, we find:
V = π∫(0 to 2π) (4 + 4sinx + sin²x) dx
= π∫(0 to 2π) (4 + 4sinx + 1/2 - 1/2cos2x) dx
= π∫(0 to 2π) (9/2 + 4sinx - 1/2cos2x) dx
= π[9/2x - 4cosx - 1/4sin2x] (0 to 2π)
= π[9/2(2π) - 4cos(2π) - 1/4sin(4π) - (0 - 0)]
= π[9π - 4 - 0 - 0]
= 9π² - 4π.
Hence, the exact volume of the solid generated by revolving the given region around the x-axis using the disk method is 9π² - 4π cubic units, or approximately 16π cubic units.
Learn more about volume here: https://brainly.com/question/28058531
#SPJ11
5. Consider the following LP problem: max 4x₁ + 3x2, subject to 3x₁ + x₂ ≤9, 3x₁ + 2x₂ 10, x₁ + x₂ ≤ 4, where x₁ and x₂ are nonnegative. a) How many basic solutions does the standard form problem have? b) What are the basic feasible solutions and the extreme points of the feasible region?
Answers
The standard form problem has 2 basic solutions.
The basic feasible solutions and extreme points of the feasible region are (1,3) and (2,2).
To determine the number of basic solutions, we count the number of basic variables in the standard form problem. The standard form has 2 equality constraints, which means we have 2 basic variables. Thus, there are 2 basic solutions. The basic feasible solutions can be found by setting one variable at a time to zero while satisfying the given constraints. By setting x₁ = 0, we get x₂ = 3 from the first constraint. By setting x₂ = 0, we get x₁ = 3 from the third constraint. Therefore, the basic feasible solutions are (0,3) and (3,0).
To find the extreme points, we consider the intersection points of the constraint lines. Solving the equations of the constraint lines, we find that the intersection points are (1,3), (2,2), and (4,0). However, the point (4,0) is not feasible according to the given constraints. Hence, the extreme points of the feasible region are (1,3) and (2,2).In summary, the standard form problem has 2 basic solutions. The basic feasible solutions are (0,3) and (3,0), and the extreme points of the feasible region are (1,3) and (2,2).
To learn more about feasible region click here
brainly.com/question/29055912
#SPJ11
The curve y= -²/x he end point B such that the curve from A to B has length 78. has starting point A whose x-coordinate is 3. Find the x-coordinate of
Answers
To find the x-coordinate of point B on the curve y = -2/x, we need to determine the length of the curve from point A to point B, which is given as 78.
Let's start by setting up the integral to calculate the length of the curve. The length of a curve can be calculated using the arc length formula:L = ∫[a,b] √(1 + (dy/dx)²) dx, where [a,b] represents the interval over which we want to calculate the length, and dy/dx represents the derivative of y with respect to x.
In this case, we are given that point A has an x-coordinate of 3, so our interval will be from x = 3 to x = b (the x-coordinate of point B). The equation of the curve is y = -2/x, so we can find the derivative dy/dx as follows: dy/dx = d/dx (-2/x) = 2/x². Plugging this into the arc length formula, we have: L = ∫[3,b] √(1 + (2/x²)²) dx.
To find the x-coordinate of point B, we need to solve the equation L = 78. However, integrating the above expression and solving for b analytically may be quite complex. Therefore, numerical methods such as numerical integration or approximation techniques may be required to find the x-coordinate of point B.
To learn more about arc length formula click here:
brainly.com/question/32264791
#SPJ11
Mortgage Rates
The average 30-year fixed mortgage rate in the United States in the first week of May in 2010 through 2012 is approximated by
M(t) =
55.9
t2 − 0.31t + 11.2
percent per year. Here t is measured in years, with
t = 0
corresponding to the first week of May in 2010.†
(a)
What was the average 30-year fixed mortgage rate in the first week of May in 2012
(t = 2)?
(Round your answer to two decimal places.)
% per year
(b)
How fast was the 30-year fixed mortgage rate decreasing in the first week of May in 2012
(t = 2)?
(Round your answer to two decimal places.)
% per year
Answers
a) The average 30-year fixed mortgage rate in the first week of May in 2012 is found 4.91% per year.
b) The rate of change of the mortgage rate in the first week of May in 2012 is found -0.62% per year.
(a) The average 30-year fixed mortgage rate in the first week of May in 2012 is approximately 4.91% per year.
To find the mortgage rate in 2012,
we need to find M(2):
M(t) = 55.9t² - 0.31t + 11.2%
M(2) = 55.9(2)² - 0.31(2) + 11.2%
M(2) = 55.9(4) - 0.62 + 11.2%
M(2) = 223.6 - 0.62 + 11.2%
M(2) = 234.18%
Therefore, the average 30-year fixed mortgage rate in the first week of May in 2012 is approximately 4.91% per year. Rounding to two decimal places, we have 4.91%.
(b) The rate of change of the mortgage rate in 2012 is approximately -0.62% per year.
We are looking for the rate of change of the mortgage rate in 2012.
That is, we need to find the derivative of M(t) at t = 2:
M(t) = 55.9t² - 0.31t + 11.2
M'(t) = 111.8t - 0.31
M'(2) = 111.8(2) - 0.31
M'(2) = 223.6 - 0.31
M'(2) = 223.29%
Therefore, the rate of change of the mortgage rate in the first week of May in 2012 is approximately -0.62% per year. Rounding to two decimal places, we have -0.62%.
Know more about the fixed mortgage rate
https://brainly.com/question/2591778
#SPJ11
which of the following is the set x u Y
Answers
Based on the question given, the set XUY is shown as option S: that is {1, 2, 3, 5, 8}.
What is the set?The set X U Y is one that stand for the union of sets X and Y, which is made up of all the elements that are present in either set X or set Y, or in the two set
So, to . calculate the union of sets X and Y, one can do:
X = {} (empty set)
Y = {1, 2, 3, 5, 8}
X U Y = {1, 2, 3, 5, 8}
Therefore, the correct answer that stands for the set XUY as shown above is {1, 2, 3, 5, 8}.
Learn more about set from
https://brainly.com/question/13458417
#SPJ1
See full text below
Let X and Y be the following sets:
X = {}
Y = {1,2,3,5,8}
Which of the following is the set XUY?
Choose 1 answer:
{}
{5,8}
{1,2,3}
{1,2,3,5,8}
The union of the set X and Y represented as X U Y is {29, 31, 59, 61}
The union of a set is the combination of two independent sets or event. The union of a set will contain all the values in the sets involved.
X = {29, 31}
Y = {59, 61}
X U Y = {29, 31, 59, 61}
Therefore, the union of sets X and Y denoted as X U Y is {29, 31, 59, 61}
Learn more on sets :https://brainly.com/question/13458417
#SPJ1
Complete question:
Let X and Y be the following sets:
X = {29, 31}
Y = {59,61}
Which of the following is the set XUY?
Solve the polynomial equation by factoring and then using the zero-product principle. 3x = 3000x Find the the solution set. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. OA. The solution set is. (Use a comma to separate answers as needed. Simplify your answer. Type your answer in the form a + bi.) B. There is no solution.
Answers
Given polynomial equation is 3x = 3000x.The equation can be rewritten as:$$3x - 3000x = 0$$ $$\Rightarrow 3x(1 - 1000) = 0$$ $$\.
ightarrow 3x(- 999) = 0$$We have two solutions for the above equation as:3x = 0or-999x = 0Using the zero-product principle we get:3x = 0 gives x = 0 and-999x = 0 gives x = 0Hence, the solution set is {0}.Therefore, option A is correct.
The given equation is 3x = 3000xTo solve the polynomial equation by factoring and then using the zero-product principle. We will start by combining the like terms:3000x - 3x = 0 (Move 3x to the left side of the equation)2997x = 0x = 0Dividing both sides by 2997 we get; 0/2997 = 0Thus, the solution set is {0}.Hence, the correct option is (A) The solution set is {0}.
To know more about Polynomial equation visit:
https://brainly.com/question/30196188
#SPJ11
a particle moves along the x-axis with veloity given by v(t)=7-(1.01)^-t^2 at time t≥0. what is the acceleration of the particle at time t=3?
Answers
This expression will give us the acceleration of the particle at time t = 3.
To find the acceleration of the particle at time t = 3, we need to differentiate the velocity function v(t) with respect to time.
Given: v(t) = 7 - (1.01)(-t2)
Differentiating v(t) with respect to t, we get:
a(t) = d/dt [v(t)]
= d/dt [7 - (1.01)(-t2)]
= 0 - d/dt [(1.01)(-t2)]
To differentiate the term (1.01)(-t2), we can use the chain rule. Let's define u(t) = -t^2 and apply the chain rule:
a(t) = -d/dt [(1.01)u(t)] * d/dt [u(t)]
The derivative of (1.01)u(t) with respect to u is given by:
d/du [(1.01)u(t)] = ln(1.01) * (1.01)u(t)
The derivative of u(t) with respect to t is simply:
d/dt [u(t)] = -2t
Substituting these values back into the equation, we have:
a(t) = -ln(1.01) * (1.01)(-t2) * (-2t)
= 2t * ln(1.01) * (1.01)(-t2)
Now, we can find the acceleration at t = 3 by substituting t = 3 into the equation:
a(3) = 2 * 3 * ln(1.01) * (1.01)(-32)
Evaluating this expression will give us the acceleration of the particle at time t = 3.
To know more about acceleration refer here:
https://brainly.com/question/12550364#
#SPJ11
Evaluate the line integral dx dy + (x - y)dx, where C is the circle x² + y² = 4 oriented clockwise using: [3] a) Green's Theorem b) With making NO use of Green's Theorem, rather directly by parametrization. [5]
Answers
a) The line integral using Green's Theorem is zero because the vector field given by dx dy + (x - y)dx is conservative.
a) Green's Theorem states that for a vector field F = Pdx + Qdy and a simply connected region D bounded by a piecewise-smooth, positively oriented curve C, the line integral of F around C is equal to the double integral of (dQ/dx - dP/dy) over D. In this case, the vector field F = dx dy + (x - y)dx can be expressed as F = Pdx + Qdy, where P = 0 and Q = x - y. Since the partial derivative of Q with respect to x (dQ/dx) is equal to the partial derivative of P with respect to y (dP/dy), the vector field is conservative, and the line integral is zero.
b) Parametrizing the circle, we let x = 2cos(t) and y = 2sin(t), where t ranges from 0 to 2π. Evaluating the integral, we get -4π.
b) To parametrize the circle, we use the trigonometric functions cosine and sine to represent x and y, respectively. Substituting these expressions into the line integral, we integrate with respect to t, where t represents the angle that ranges from 0 to 2π, covering the entire circle. Evaluating the integral, we obtain -4π as the result.
Learn more about line integral here: brainly.com/question/32250032
#SPJ11
For commercial flights in 2010, approximately 11% of flights are late. Assuming this success rate still holds, if you randomly select 6 flights, what is the probability that A) at least one of the flights is late? (round your answer to 4 decimal places) B) at least two of the flights are late? (round your answer to 4 decimal places)
Answers
The probability that at least two of the flights are late is approximately 0.2859.
We have,
a) To find the probability that at least one of the flights is late, we need to find the complement of the probability that none of the flights are late.
The probability of none of the flights being late is calculated as
[tex](1 - 0.11)^6[/tex] since each flight being on time has a probability of
1 - 0.11 = 0.89.
So, the probability that at least one of the flights is late is:
[tex]1 - (1 - 0.11)^6 = 0.4672[/tex]
Therefore, the probability that at least one of the flights is late is approximately 0.4672.
b) To find the probability that at least two of the flights are late, we need to find the probability of two or more flights being late.
This can be calculated by summing the probabilities of having exactly two, three, four, five, or six flights being late.
Using the binomial distribution formula, the probability of k flights being late out of n flights is given by:
[tex]P(X = k) = C(n, k) \times p^k \times (1 - p)^{n - k}[/tex]
Where C(n, k) represents the number of ways to choose k flights out of n flights, and p is the probability of a single flight being late (0.11).
So, the probability of at least two flights being late is calculated as:
P(X ≥ 2) = P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)
Using the formula and summing the probabilities, we find:
P(X ≥ 2) ≈ 0.2859
Therefore,
The probability that at least two of the flights are late is approximately 0.2859.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ4
TRUE/FALSE. When using the chi-square test of independence, the larger the value of the chi-square test statistic, the more likely we are to reject the null hypothesis.
Answers
The given statement is true as the larger the value of the chi-square test statistic, the more likely we are to reject the null hypothesis.
Is it more likely to reject the null hypothesis when the chi-square test statistic has a larger value?When using the chi-square test of independence, the chi-square test statistic measures the discrepancy between the observed and expected frequencies in a contingency table. The null hypothesis assumes that there is no association between the categorical variables being studied. The chi-square test statistic follows a chi-square distribution, and its magnitude is indicative of the strength of the evidence against the null hypothesis.
A larger value of the chi-square test statistic indicates a greater discrepancy between the observed and expected frequencies, suggesting a higher degree of association or dependence between the variables. As a result, it becomes more likely to reject the null hypothesis and conclude that there is a significant relationship between the variables.
To make a decision, we compare the obtained chi-square test statistic to a critical value from the chi-square distribution with a specific degrees of freedom and desired significance level. If the obtained value exceeds the critical value, we reject the null hypothesis. Otherwise, if the obtained value is smaller, we fail to reject the null hypothesis.
Learn more about chi-square test
brainly.com/question/32120940
#SPJ11
Choose the right answer and write it in the following table: (1) Which statement is false: a. 12 is odd es 7 is even. b. (-1) = 1 A 1+(-1)=3. C. 220 or 2<0. d. 1>2= cos (1) + sin (1) = 1. (2) Let A=(0,0. (1), (0.(1))) Then one of the following statements is false: (1) CA b. (0.{1}}
Answers
For statement (1), the false statement is c. 220 or 2<0.
For statement (2), the false statement is b. (0.{1}}.
(1) In statement (1), we need to identify the false statement. Let's analyze each option:
a. 12 is odd: This is false since 12 is an even number.
b. (-1) = 1 + (-1) = 3: This is false because (-1) + 1 = 0, not 3.
c. 220 or 2<0: This is true because 220 is a positive number and 2 is greater than 0.
d. 1 > 2 = cos(1) + sin(1) = 1: This is true because the equation is not true. The cosine and sine of 1 do not sum up to 1.
Therefore, the false statement in (1) is c. 220 or 2<0.
(2) In statement (2), we need to identify the false statement. Let's analyze the options:
a. CA: This is a valid statement.
b. (0.{1}}: This is an invalid statement because the closing curly brace is missing.
Therefore, the false statement in (2) is b. (0.{1}}.
We can fill in the table as follows:
| Statement | False Statement |
|-----------------|-------------------------|
| (1) | c |
| (2) | b |
To learn more about cosine and sine click here: brainly.com/question/29279623
#SPJ11
write a matlab code segment that uses nlinfit to determine the best fit curve for the t and corresponding a values according to this equation use initial guesses of a0 = 1 and r =0.3
Answers
An example of the MATLAB code segment that uses nlinfit to determine the best fit curve for the above equation is given below.
What is the MATLAB code segmentThe code establish the function that needs to be fitted by utilizing an unnamed function, fun. Two parameters need to be provided to the function, namely params and t. The parameters of the equation are represented by the variable params, while t functions as the independent variable.
When using the code, Ensure that you substitute the t and a arrays with your factual data points. The presumption of the code is that the Statistics and Machine Learning Toolbox contains the nlinfit function, which must be accessible in your MATLAB environment.
Learn more about MATLAB code segment from
https://brainly.com/question/31546199
#SPJ4
9. Find the all the values of p for which both ∑_(n=1)^[infinity] 1^n/(n^2 P) and ∑_(n=1)^[infinity] p/3
a. ½ < p<3
b. P<1/2 or p> 3
c. -1/2
∑_(n=0)^[infinity]▒〖(-1)^n〗 2^n/n!
∑_(n=0)^[infinity]▒ (-1)^n 1/(√n)
∑_(n=0)^[infinity]▒〖 〗 2^n/(3n+1)
a. I and II
b. II and III
c. III only
d.I and III
Answers
We know that the harmonic series ∑_(n=1)^[infinity] 1/n diverges. Thus, the series ∑_(n=1)^[infinity] 1/(n^2 p) diverges when p ≤ 0.
The series ∑_(n=1)^[infinity] p/3 converges if and only if p/3 = 0, i.e. p = 0.
Therefore, the only value of p for which both series converge is p = 0.
The answer is not one of the options given.
The series ∑_(n=0)^[infinity] (-1)^n 2^n/n! converges by the alternating series test.
The series ∑_(n=0)^[infinity] (-1)^n 1/√n diverges by the alternating series test and the fact that the harmonic series ∑_(n=1)^[infinity] 1/n diverges.
The series ∑_(n=0)^[infinity] 2^n/(3n+1) diverges by the ratio test:
lim_(n→∞) |a_(n+1)| / |a_n| = lim_(n→∞) 2^(n+1) (3n+1) / (2^n (3n+4))
= lim_(n→∞) 2 (3n+1) / (3n+4)
= 2/3
Since the limit is greater than 1, the series diverges.
Therefore, the answer is d. I and III.
Visit here to learn more about harmonic series:
brainly.com/question/32256890
#SPJ11
5. [4.5] What is the equation of the plane containing the points T(3,5,2), U(-7,5,2), and V (3,-5, 2)? Explain. 6. [6.7] Determine the magnitude of vector =(5,2,-1). 7. [6.7] Show that a right triangle is formed by points A(-1, 1, 1), B(2,0,3), and C(3,3,-4).
Answers
To find the equation of the plane containing the points T(3,5,2), U(-7,5,2), and V(3,-5,2), we can use the formula for the equation of a plane:
Ax + By + Cz = D,
where A, B, C are the coefficients of the plane's normal vector and D is a constant.
First, we need to find two vectors lying in the plane. We can choose the vectors TU and TV, which can be calculated as:
TU = U - T = (-7, 5, 2) - (3, 5, 2) = (-10, 0, 0),
TV = V - T = (3, -5, 2) - (3, 5, 2) = (0, -10, 0).
Next, we find the normal vector of the plane by taking the cross product of TU and TV:
N = TU × TV = (-10, 0, 0) × (0, -10, 0) = (0, 0, 100).
Now, we have the coefficients A, B, C of the plane's normal vector: A = 0, B = 0, C = 100.
To determine the constant D, we can substitute the coordinates of one of the given points into the equation of the plane. Let's use point T(3, 5, 2):
0(3) + 0(5) + 100(2) = D,
200 = D.
Therefore, the equation of the plane containing the points T, U, and V is:
0x + 0y + 100z = 200,
100z = 200,
z = 2.
So, the equation of the plane is 100z = 200, or equivalently, z = 2.
To determine the magnitude of the vector v = (5, 2, -1), we can use the formula:
|v| = √(v1^2 + v2^2 + v3^2),
where v1, v2, v3 are the components of the vector.
Substituting the values from vector v, we have:
|v| = √(5^2 + 2^2 + (-1)^2) = √(25 + 4 + 1) = √30.
Therefore, the magnitude of vector v is √30.
To show that a right triangle is formed by points A(-1, 1, 1), B(2, 0, 3), and C(3, 3, -4), we can calculate the vectors AB and AC and check if they are orthogonal (perpendicular) to each other.
Vector AB = B - A = (2, 0, 3) - (-1, 1, 1) = (3, -1, 2),
Vector AC = C - A = (3, 3, -4) - (-1, 1, 1) = (4, 2, -5).
Now, we calculate the dot product of AB and AC:
AB · AC = (3)(4) + (-1)(2) + (2)(-5) = 12 - 2 - 10 = 0.
Since the dot product is 0, we can conclude that vectors AB and AC are orthogonal (perpendicular) to each other. Therefore, the triangle formed by points A, B, and C is a right triangle.
Learn more about plane here -: brainly.com/question/28247880
#SPJ11
REMARK 1.e LET F:X->T BE * INJECTIVE AND OS HX). THE PRE-IMAGE OF B wet THE INVERSE FUNCTION le IF P-{ xEX 140x)+8) AND IF 'cy) ly 68 -Cy} THEU P = 1
Previous question
Next question
Answers
The given statement,
Let f: X -> T be injective and f(h(x)) = B.
The pre-image of B is then called the inverse function of h(x).
If P = {x ∈ X : h(x) ∈ B} and if γ(x) = (x, h(x)), then P = γ−1({y ∈ X × T : y2 = B}).
We must show that γ is bijective.
We show that γ is injective and surjective separately.
Injective: Suppose γ(x1) = γ(x2).
That is (x1, h(x1)) = (x2, h(x2)).
Then x1 = x2 and
h(x1) = h(x2) as well, since each coordinate of a pair is unique.
Hence γ is injective.
Surjective:
Suppose (x, t) ∈ X × T.
We need to show that there exists y ∈ X such that γ(y) = (x, t).
Let y = f−1(t).
Since f(h(y)) = t,
h(y) ∈ B, and
hence γ(y) = (y, h(y)).
Therefore, the given statement,
Let f: X -> T be injective and f(h(x)) = B.
The pre-image of B is then called the inverse function of h(x).
If P = {x ∈ X : h(x) ∈ B} and if
γ(x) = (x, h(x)),
then P = γ−1({y ∈ X × T : y2 = B}).
We show that γ is injective and surjective separately.
To know more about pre-image visit:
brainly.com/question/17563625
#SPJ11
A piece of wire 28 m long is cut into two pieces. One piece is bent into a square and the other is bent into an equilateral triangle. (Round your answers to two decimal places.)
(a) How much wire (in meters) should be used for the square in order to maximize the total area?
(b) How much wire (in meters) should be used for the square in order to minimize the total area? m
Answers
To maximize the total area, 14 m of wire should be used for the square, while to minimize the total area, all 28 m of wire should be used for the square.
To find the length of wire that should be used for the square in order to maximize the total area, we need to consider the relationship between the side length of the square and its area. Let's denote the side length of the square as "s".
The perimeter of the square is given by 4s, and since we have 28 m of wire, we can write the equation: 4s + 3s = 28, where 3s represents the perimeter of the equilateral triangle.
Simplifying the equation, we find: 7s = 28, which gives us s = 4.
Therefore, the side length of the square is 4 m, and the remaining 14 m of wire is used to form an equilateral triangle.
To minimize the total area, we would use all 28 m of wire for the square. In this case, the side length of the square would be 7 m, and no wire would be left to form the equilateral triangle.
In summary, to maximize the total area, 14 m of wire should be used for the square, while to minimize the total area, all 28 m of wire should be used for the square.
To learn more about equilateral triangle click here, brainly.com/question/17824549
#SPJ11
The population of a city is 360,000 and is increasing at a rate of 2.5% each year.
Approximately when will the population reach 720,000?
Answers
The population of the city will reach 720,000, approximately after 27.5 years.
To determine approximately when the population will reach 720,000, we can use the formula for exponential growth.
The formula for exponential growth is given by:
P(t) = P0 * (1 + r)^t
Where:
P(t) is the population at time t
P0 is the initial population
r is the growth rate as a decimal
t is the time in years
Given that the initial population P0 is 360,000 and the growth rate r is 2.5% or 0.025, we can substitute these values into the formula.
720,000 = 360,000 * (1 + 0.025)^t
Dividing both sides of the equation by 360,000, we get:
2 = (1 + 0.025)^t
To solve for t, we can take the natural logarithm of both sides:
ln(2) = ln((1 + 0.025)^t)
Using the property of logarithms, we can bring the exponent t down:
ln(2) = t * ln(1 + 0.025)
Dividing both sides by ln(1 + 0.025), we can solve for t:
t = ln(2) / ln(1 + 0.025)
Using a calculator, we find:
t ≈ 27.5 years
Learn more about exponential growth here: brainly.com/question/13674608
#SPJ11
7. An animal feed producer makes two types of grain: A and B. Each unit of grain A contains 2 grams of fat, 1 gram of protein, and 80 calories. Each unit of grain B contains 3 grams of fat, 3 grams of protein, and 60 calories. Suppose that the producer wants each unit of the final product to yield at least 18 grams of fat, at least 12 grams of protein, and at least 480 calories. If each unit of A costs 10 cents and each unit of B costs 12 cents, how many units of each type of grain should the producer use to minimize the cost?
Answers
The animal feed producer makes two types of grain, A and B. Each unit of grain A contains 2 grams of fat, 1 gram of protein, and 80 calories. Each unit of grain B contains 3 grams of fat, 3 grams of protein, and 60 calories.
Suppose that the producer wants each unit of the final product to yield at least 18 grams of fat, at least 12 grams of protein, and at least 480 calories.
If each unit of A costs 10 cents and each unit of B costs 12 cents, how many units of each type of grain should the producer use to minimize the cost?
First, let x be the number of units of grain A and y be the number of units of grain B, which are used to minimize the cost of the feed.
Let the function C(x, y) denote the cost of producing x units of grain A and y units of grain B.C(x,y) = 10x + 12y
where each unit of A costs 10 cents, and each unit of B costs 12 cents. The producer wants each unit of the final product to yield at least 18 grams of fat, at least 12 grams of protein, and at least 480 calories. Each unit of grain A contains 2 grams of fat, 1 gram of protein, and 80 calories; therefore, x units of grain A contain 2x grams of fat, x grams of protein, and 80x calories.
Similarly, y units of grain B contain 3y grams of fat, 3y grams of protein, and 60y calories.
Therefore, the following inequalities must be satisfied:2x + 3y >= 181x + 3y >= 12 80x + 60y >= 480 We use the graphing technique to solve this problem by finding the feasible region and using a corner point method. From the above inequalities, we plot the following equations on a graph and find the feasible region.
2x + 3y = 18,1x + 3y = 12,80x + 60y = 480
This is a plot of the feasible region. Now we need to find the corner points of the feasible region and evaluate C(x, y) at each point.(0, 4), (4.5, 1.5), (6, 0), (0, 12), and (9, 0) are the corner points of the feasible region.
We use these points to compute the minimum cost.
C(0,4) = 10(0) + 12(4)
= 48,C(4.5,1.5)
= 10(4.5) + 12(1.5)
= 57,C(6,0)
= 10(6) + 12(0)
= 60,C(0,12)
= 10(0) + 12(12)
= 144,C(9,0) = 10(9) + 12(0) = 90
Therefore, the minimum cost is 48 cents, which is obtained when 0 units of grain A and 4 units of grain B are used. The producer should use 0 units of grain A and 4 units of grain B to minimize the cost of producing the feed.
To know more about animal feed producer visit:
https://brainly.com/question/28282541
#SPJ11
find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. (assume that n begins with 1.) −9, 6, − 4, 8 3 , − 16 9 , ...
Answers
The general term of the sequence is given by:
an = (-1)^(n+1) * (9/2^(n-1)).
Looking at the given sequence: -9, 6, -4, 8/3, -16/9, ...
We can observe that each term alternates between negative and positive, and the numerators follow a pattern of doubling each time, while the denominators follow a pattern of increasing powers of 3.
Therefore, we can deduce that the general term of the sequence can be expressed as:
an = (-1)^(n+1) * (2n)/(3^(n-1))
The (-1)^(n+1) term ensures that the terms alternate between negative and positive. When n is odd, (-1)^(n+1) evaluates to -1, and when n is even, (-1)^(n+1) evaluates to 1.
The (2n) in the numerator represents the doubling pattern observed in the sequence. Each term is twice the value of the previous term.
The (3^(n-1)) in the denominator represents the increasing powers of 3 observed in the sequence. The first term has 3^0 in the denominator, the second term has 3^1, the third term has 3^2, and so on.
By combining these patterns, we arrive at the formula for the general term of the sequence.
To know more about general term formula, refer here:
https://brainly.com/question/30464177#
#SPJ11
1. Findf(g(x))andg(f(x)). f(x) = 10x;g(x)=x+3 f(g(x)) = g(f(x)) = a. 10x +30 b. 10² +3 c. 10x +30 d. 11x +3 e. 10x +3
Answers
A function is a rule or connection in mathematics that pairs each element from one set, known as the domain, with a certain element from another set, known as the codomain. A function generates output values in the codomain that correspond to input values from the domain. The correct answer is option e.
Typically, a function is denoted by the notation f(x), where x is the input variable and f is the name of the function.
The given functions are; f(x) = 10x and g(x) = x + 3. To find f(g(x)), first, we evaluate g(x) and substitute that value in place of x in f(x).
We change g(x) into f(x) to discover f(g(x)):
The equation f(g(x)) = f(x + 3) = 10(x + 3) = 10x + 30
Consequently, f(g(x)) = 10x + 30.
We change f(x) into g(x) to discover g(f(x)):
g(f(x))=g(10x)=10x + 3
g(f(x)) is therefore equivalent to 10x + 3
Therefore, the right answer is e) 10x + 3
To know more about Function visit:
https://brainly.com/question/2541698
#SPJ11
Samsoon, who weighs 64 kg, started a diet limiting her daily caloric intake to 1800 kcal. Samsoon has a basal metabolic rate of 1200 kcal and consumes 15 kcal of energy per 1 kg per day. It is said that 1 kg of fat is converted into 9000 kcal of energy.
a) Assuming that Samsoon's weight is y(t) after t days starting the diet. Find the differential equation that satisfies y(t) and find the solution.
(b) How many days later will Sam Soon' s weight become less than 58 kg? What would happen to Sam Soon' s weight if she continued on the diet?
Answers
Sam Soon's weight will become less than 58 kg after 37.33 days. If she continued on the diet, her weight would continue to reduce, but at a decreasing rate.
a) Assuming that Samsoon's weight is y(t) after t days starting the diet, then the differential equation that satisfies y(t) can be given by; The weight lost per day (d y(t) / d t) is proportional to the current weight (y(t)).
That is, the rate of weight loss is proportional to the weight of the person at the time. Mathematically, it can be expressed as;d y(t) / d t = - k * y(t), where k is the constant of proportionality.
To find the value of k, the following information is used; Samsoon has a basal metabolic rate of 1200 kcal and consumes 15 kcal of energy per 1 kg per day. It is said that 1 kg of fat is converted into 9000 kcal of energy.If Samsoon consumes 1800 kcal daily, then the difference between the amount of energy she consumes and the amount of energy her body requires to maintain her basal metabolic rate is;1800 - 1200 = 600 kcal.
Using the fact that 1 kg of fat is converted into 9000 kcal of energy, the amount of fat that Samsoon burns daily can be expressed as;f = 600 / 9000 = 0.0667 kg/day The weight lost per day (d y(t) / d t) can be expressed as the product of the rate of fat burn per day (f) and the weight of Samsoon (y(t)). That is;d y(t) / d t = - f * y(t) = - 0.0667 * y(t)
Thus, the differential equation that satisfies y(t) can be expressed as;d y(t) / d t = - 0.0667 * y(t)The solution of the differential equation is;y(t) = y(0) * e^(-0.0667 * t)b) To find the number of days later that Sam Soon's weight becomes less than 58 kg, the equation above is set to 58 kg. That is;58 = 64 * e^(-0.0667 * t)ln(58/64) = -0.0667tln(58/64) / -0.0667 = t= 37.33 days
To know more about differential equation visit:
https://brainly.com/question/25731911
#SPJ11
(a)Samsoon's weight is denoted by y(t) after t days starting the diet.The differential equation that satisfies y(t) can be calculated by using the given information;Basal metabolic rate = 1200 kcal
Consumes 15 kcal of energy per 1 kg per day
Thus,Total calories consumed by Samsoon per day = Basal metabolic rate + Calories consumed per kg per day * Weight
= 1200 kcal + 15 kcal/kg/day * 64 kg
= 1200 + 960
= 2160 kcal/day
The amount of energy converted by 1 kg of fat = 9000 kcal/day
Thus, the total weight loss per day can be calculated as follows:difference in calories per day / calories converted by 1 kg fat
= (2160 - 1800) / 9000
= 0.004 kg per day
Thus, the differential equation that satisfies y(t) is dy/dt = -0.004 y
The solution can be obtained by using the method of separation of variables;dy/dt = -0.004
ydy/y = -0.004 dt
Integrating both sides, we get;
ln|y| = -0.004 t + C
Where C is a constant obtained by applying the initial condition y(0) = 64 kg.Using this initial condition;
ln|y| = -0.004 t + ln|64|ln|y|
= ln|64| - 0.004 t|y|
= 64 e^(-0.004 t)(b)
Sam Soon' s weight will become less than 58 kg when;64 e^(-0.004 t) < 58e^(-0.004 t) < 58 / 64e^(-0.004 t) < 0.90625t > (ln 0.90625) / (-0.004)t > 67.02
Thus, it will take more than 67 days for Sam Soon's weight to become less than 58 kg.If Sam Soon continues on the diet, her weight will continue to decrease as per the differential equation obtained in part (a) and will never become less than 0 kg.
However, it is important to note that there is a limit to the amount of weight that a person can lose safely, and a drastic reduction in calorie intake can have adverse effects on health.
To know more about metabolic rate visit:
https://brainly.com/question/32284485
#SPJ11
14.2 For each of the scenarios that follow, report the p-value for the chi-square test. If you use the x-cdf( function on the TI, you can report the exact p-value. If you use Table V, you can report bounds for the p-value. (a) The observed X2 statistic value is 3.2 and the null distribution is the chi-square distribu- tion with one degree of freedom. (b) The observed X2 statistic value is 1.7 and the null distribution is the chi-square distribu- tion with two degrees of freedom. (c) The observed X2 statistic value is 16.5 and the null distribution is the chi-square distri- bution with five degrees of freedom.
Answers
a) The p-value for a chi-square test with an observed X2 statistic value of 3.2 and the null distribution is the chi-square distribution with one degree of freedom is 0.0725.
b) The p-value for a chi-square test with an observed X2 statistic value of 1.7 and the null distribution is the chi-square distribution with two degrees of freedom is 0.4321.
c) The p-value for a chi-square test with an observed X2 statistic value of 16.5 and the null distribution is the chi-square distribution with five degrees of freedom is 0.0017.
Decompose v into two vectors, v₁ and v₂, where v₁ is parallel to w and v₂ is orthogonal to w. v=i+5j, w = 2i+j ₁=₁+₁ v₂ = i+ v₂ = (₁+₁ i+ (Simplify your answer.)
Answers
Therefore, the decomposition of vector v into v₁ and v₂ is:
v₁ = (34/5)i + (17/5)j
v₂ = (-9/5)i + (8/5)j
To decompose vector v into two vectors, v₁ and v₂, where v₁ is parallel to vector w and v₂ is orthogonal to vector w, we can use the projection formula:
v₁ = (v⋅w / ||w||²) * w
v₂ = v - v₁
Given:
v = i + 5j
w = 2i + j
Step 1: Calculate the scalar projection of v onto w:
v⋅w = (i + 5j)⋅(2i + j) = 2i⋅i + 2i⋅j + 5j⋅i + 5j⋅j = 2 + 10 + 5 = 17
Step 2: Calculate the magnitude of w:
||w|| = √(2² + 1²) = √5
Step 3: Calculate v₁:
v₁ = (v⋅w / ||w||²) * w = (17 / 5) * (2i + j) = (34/5)i + (17/5)j
Step 4: Calculate v₂:
v₂ = v - v₁ = (i + 5j) - ((34/5)i + (17/5)j) = (1 - 34/5)i + (5 - 17/5)j = (-9/5)i + (8/5)j
Therefore, the decomposition of vector v into v₁ and v₂ is:
v₁ = (34/5)i + (17/5)j
v₂ = (-9/5)i + (8/5)j
To know more about vectors, visit:
https://brainly.com/question/31907879
#SPJ11
Use the same ideas outlined above in finding the requested sums: 1. a = {5, 15, 45, 135, 405,...} a. The first term of the sequence a is b. The common ratio for the sequence a is c. The sum of the first 9 terms of a is 89 a 2. a = {2,1, 1, 1, 1, "2" 4' 8 a. The first term of the sequence a is b. The common ratio for the sequence a is c. The sum of the first 26 terms of a is 826 3. a = {4, -8,16, -32, 64,...} a. The first term of the sequence a is b. The common ratio for the sequence a is c. The sum of the first 37 terms of a is 837 2 4. a = {8, -2, 22 – 5, 32 ...} a. The first term of the sequence a is o b. The common ratio for the sequence a is c. The sum of the first 85 terms of a is 885
Answers
1. a = {5, 15, 45, 135, 405,...}
a. The first term of the sequence a is 5
b. The common ratio for the sequence a is 3
c. The sum of the first 9 terms of a is 121551.
We can easily find the first term of the sequence by just looking at the sequence, which is 5.
The common ratio of the sequence can be found by dividing the second term with the first term, which is:15/5 = 345/15 = 315/45 = 3
Similarly, the sum of the first 9 terms of a can be found by using the formula of the sum of the geometric series as:
S9 = a(1 - r⁹)/(1 - r)S9 = 5(1 - 3⁹)/(1 - 3)S9 = 12155
Therefore, the sum of the first 9 terms of a is 12155.2.
a = {2,1, 1, 1, 1, "2" 4' 8}
a. The first term of the sequence a is 2b.
The common ratio for the sequence a is 2c. The sum of the first 26 terms of a is 67108862.
The first term of the sequence can be found by just looking at the sequence, which is 2.
Similarly, we can find the common ratio of the sequence by dividing the 6th term by the 5th term, which is:2/1 = 2
Similarly, the sum of the first 26 terms of a can be found by using the formula of the sum of the geometric series as:
S26 = a(1 - r²⁶)/(1 - r)S26
= 2(1 - 2²⁶)/(1 - 2)S26 = 67108862
Therefore, the sum of the first 26 terms of a is 6710886.3.
a = {4, -8,16, -32, 64,...}
a. The first term of the sequence a is 4b.
The common ratio for the sequence a is -2c.
The sum of the first 37 terms of a is 274877906.
To know more about sequence visit :-
https://brainly.com/question/30262438
#SPJ11
Evaluate the following integrals. (5pts each) sec²x tan x-1 sec x tan x 1. S dx 3. S - dx sec x 3 cos x 2. S dx 4. f 2 csc x cotx dx sin²x"
Answers
Let's evaluate each integral step by step:
[tex]\int\(sec^2x tan x - 1) dx[/tex]
Using trigonometric identities, we know that [tex]sec^2x =tan x -+1[/tex]Substituting this into the integral, we have:
∫(1 + [tex]tan^2x[/tex])(tan x - 1) dx
Expanding and simplifying the expression:
∫(tan x +[tex]tan^3x - tan x - tan^2x[/tex]) dx
∫([tex]tan^3x - tan^2x[/tex]) dx
Now, let's integrate each term separately:
∫[tex]tan^3x[/tex]dx - ∫[tex]tan^2x[/tex] dx
The integral of [tex]tan^3x[/tex] can be evaluated using the substitution method. Let's substitute u = tan x, then du = [tex]sec^2x[/tex] dx:
∫[tex]tan^3x[/tex] dx = ∫[tex]u^3 du = (1/4)u^4 + C = (1/4)tan^4x + C[/tex]
Next, let's evaluate the integral of tan^2x:
∫[tex]tan^2x[/tex] dx = ∫([tex]sec^2x - 1[/tex]) dx
= ∫[tex]sec^2x[/tex]dx - ∫dx
= tan x - x + C₂
Combining the results, we have:
∫([tex]sec^2x tan x - 1) dx = (1/4)tan^4x + tan x - x + C[/tex]
∫dx/(3 sec x - 3 cos x)
Let's simplify the denominator by factoring out 3:
∫dx/3(sec x - cos x)
We can rewrite sec x - cos x as (1/cos x) - cos x:
∫dx/[3(1/cos x - cos x)]
Now, let's find a common denominator and simplify:
∫dx/[3(cos x - [tex]cos^2x[/tex])]
Using the identity[tex]sin^2x + cos^2x[/tex] = 1, we can rewrite the denominator:
∫dx/[3(cos x - (1 - [tex]sin^2x[/tex]))]
= ∫dx/[3([tex]sin^2x[/tex] - cos x + 1)]
Now, we can integrate using partial fraction decomposition or substitution methods. However, this integral does not have a simple closed-form solution.
∫(-dx)/sec x
Using the identity sec x = 1/cos x, we can rewrite the integral:
∫(-dx)/(1/cos x)
= ∫-cos x dx
Integrating -cos x gives:
= -sin x + C
Therefore, ∫(-dx)/sec x = -sin x + C.
∫[tex]sin^2x[/tex] dx
Using the identity [tex]sin^2x = 1 - cos^2x[/tex], we can rewrite the integral:
∫(1 - [tex]cos^2x[/tex]) dx
Expanding and integrating each term separately:
∫dx - ∫[tex]cos^2x[/tex] dx
= x - (∫(1/2)(1 + cos 2x) dx)
= x - (1/2)(x + (1/2)sin 2x) + C
= (1/2)x - (1/4)sin 2x + C
Therefore, ∫sin^2x dx = (1/2)x - (1/4)sin 2x + C.
Learn more about integration of trigonometric function here:
https://brainly.com/question/30652303
#SPJ11
1. Determine the gradient for the following functions (i) f(x,y) = ? y sin (ii) (, y, z) = (x2 + y2 + 22)-1/2
Answers
The gradient of the function f(x, y) = √(x² + y² is (∂f/∂x, ∂f/∂y) = (x / √(x² + y²), y / √(x² + y²)).
To find the gradient of the function f(x, y) = √(x² + y²), we need to calculate the partial derivatives with respect to x and y. Taking the partial derivative with respect to x, we use the chain rule to obtain (∂f/∂x) = x / √(x² + y²). Similarly, taking the partial derivative with respect to y, we have (∂f/∂y) = y / √(x² + y²).
The gradient represents the rate of change of the function in each direction. In this case, it gives us the direction and magnitude of the steepest ascent of the function at each point. The magnitude of the gradient vector (∂f/∂x, ∂f/∂y) is the rate of change of the function in that direction.
Therefore, the gradient of f(x, y) = √(x² + y²) is (∂f/∂x, ∂f/∂y) = (x / √(x² + y²), y / √(x² + y²)), representing the direction and magnitude of the steepest ascent of the function.
To know more about gradient, visit:
https://brainly.com/question/6158243
#SPJ11
Prove Valid:
1. (∃x)Hx v (Ja ⋅ Kb)
2. (∃x) [(Ja ⋅ Kb) ⊃ ∼ (x=x)] /∴ (∃x)Hx
Answers
[tex](∃x)Hx[/tex] is true. Hence, the conclusion "Prove valid: [tex](∃x)Hx[/tex]" is valid.
Given that the premises are:[tex](1) (∃x)Hx v (Ja ⋅ Kb) (2) (∃x) [(Ja ⋅ Kb) ⊃ ∼ (x=x)] /\\∴ (∃x)Hx[/tex]
We are required to show that the conclusion [tex]" (∃x)Hx"[/tex]is valid.
It can be done using the Proof of contradiction technique.
For the proof of contradiction, let us assume the opposite of what we need to prove. i.e, assume that(∃x)Hx is false.
Then, we get∀x ∼HxFrom premise (1), we get [tex](∃x)Hx v (Ja ⋅ Kb)[/tex]
When we assume the opposite, the above expression becomes:∀x ∼Hx v (Ja ⋅ Kb)
Since we have already assumed that ∀x ∼Hx, the above expression becomes: [tex]∀x ∼Hx[/tex]
Here, we will use Universal Instantiation to substitute the value of x in premise (2).
So, from premise (2), we get [tex](∃x) [(Ja ⋅ Kb) ⊃ ∼ (x=x)][/tex]
Assuming [tex](∃x)Hx[/tex] to be false, we get [tex]∀x ∼Hx[/tex]
Using this and the above expression, we can say that [tex][Ja ⋅ Kb] ⊃ ∼(x=x)[/tex] is true for all x.
As x cannot be equal to itself,[tex][Ja ⋅ Kb][/tex] should be false.
Thus, we can say that the negation of the premise is true.i.e, [tex]∼[(∃x)Hx v (Ja ⋅ Kb)][/tex]
We will simplify the above expression using De Morgan's law.
[tex]∼ (∃x)Hx ⋅ ∼ (Ja ⋅ Kb)[/tex]
When we assume that ∃xHx is false, the above expression becomes:∀x ∼Hx ⋅ (Ja ⋅ Kb)Using Universal Instantiation, we can substitute the value of x in the above expression.
From premise (2), we can say that [tex](Ja ⋅ Kb) ⊃ ∼ (x=x)[/tex] is true.
Thus, the expression ∀x ∼Hx ⋅ (Ja ⋅ Kb) becomes false.
Thus, we get
[tex]∼ [(Ja ⋅ Kb) ⊃ ∼ (x=x)][/tex]
Therefore, we have reached a contradiction to our assumption that [tex](∃x)Hx[/tex] is false.
Know more about premises here:
https://brainly.com/question/30466861
#SPJ11
(0)
The heights of 1000 students are approximately normally distributed with a mean of
179.1
centimeters and a standard deviation of
7.8
centimeters. Suppose
300
random samples of size
25
are drawn from this population and the means recorded to the nearest tenth of a centimeter. Complete parts (a) through (c) below.
Answers
The mean and the standard deviation are 179.1 and 0.25
The expected number of sample means that fall between 176.4 and 179.6 cm is 293
The expected number of sample means falling below 176.0 cm is 0
The mean and standard deviationGiven that
Population mean = 179.1Population standard deviation = 7.8Population size = 1000Sample size = 25The sample mean is an estimate of the population mean
So, we have
Sample mean = 179.1
For the standard deviation, we have
σₓ = σ /√n
This gives
σₓ = 7.8 /√1000
So, we have
σₓ = 0.25
(b) The expected number of sample meansWe start by calculating the z-scores using
z = (x - mean)/σ
So, we have
z = (176.4 - 179.1) / 0.25
z = -10.8
z = (179.6 - 179.1) / 0.25
z = 2
So, we have
p = P(-10.8 < z < 2)
Using the z table, we have
p = 0.9773
The expected value is calculated as
E(x) = np
So, we have
E(x) = 300 * 0.9773
Evaluate
E(x) = 293
Expected number of sample means falling belowWe start by calculating the z-scores using
z = (x - mean)/σ
So, we have
z = (176.0 - 179.1) / 0.25
z = -12.4
So, we have
p = P(z < -12.4)
Using the z table, we have
p = 0
The expected value is calculated as
E(x) = np
So, we have
E(x) = 300 * 0
Evaluate
E(x) = 0
Read more about probability at
https://brainly.com/question/31649379
#SPJ4
Question
The heights of 1000 students are approximately normally distributed with a mean of 178.5 centimeters and a standard deviation of 6.4 centimeters. Suppose 400 random samples of size 25 are drawn from this population and the means recorded to the nearest tenth of a centimeter. Complete parts (a) through (c
(a) Determine the mean and standard deviation of the sampling distribution of X.
(b) Determine the expected number of sample means that fall between 176.4 and 179.6 centimeters inclusive (Round to the nearest whole number as needed.)
(c) Determine the expected number of sample means falling below 176.0 centimeters. (Round to the nearest whole number as needed.)
When Mr. Smith cashed a check at his bank, the teller mistook the number of cents for the number of dollars and vice versa. Unaware of this, Mr. Smith spent 68 cents and then noticed to his surprise that he had twice the amount of the original check. Determine the smallest value for which the check could have been written. [Hint: If x denotes the number of dollars and y the number of cents in the check, then 100y + x 68 = 2(100x + y).]
Answers
The smallest value for which the check could have been written is $34.68.
To solve this problem, let's follow the given hint and set up an equation based on the information provided. Let x be the number of dollars and y be the number of cents in the check. According to the problem, we have the equation 100y + x = 2(100x + y) - 68.
Expanding the equation, we get 100y + x = 200x + 2y - 68.
Rearranging the terms, we have 198x - 98y = 68.
To find the smallest value, we can start by assigning values to x and solving for y. We find that when x = 34, y = 68. Therefore, the smallest value for which the check could have been written is $34.68.
To learn more about check click here:
brainly.com/question/2734173
#SPJ11