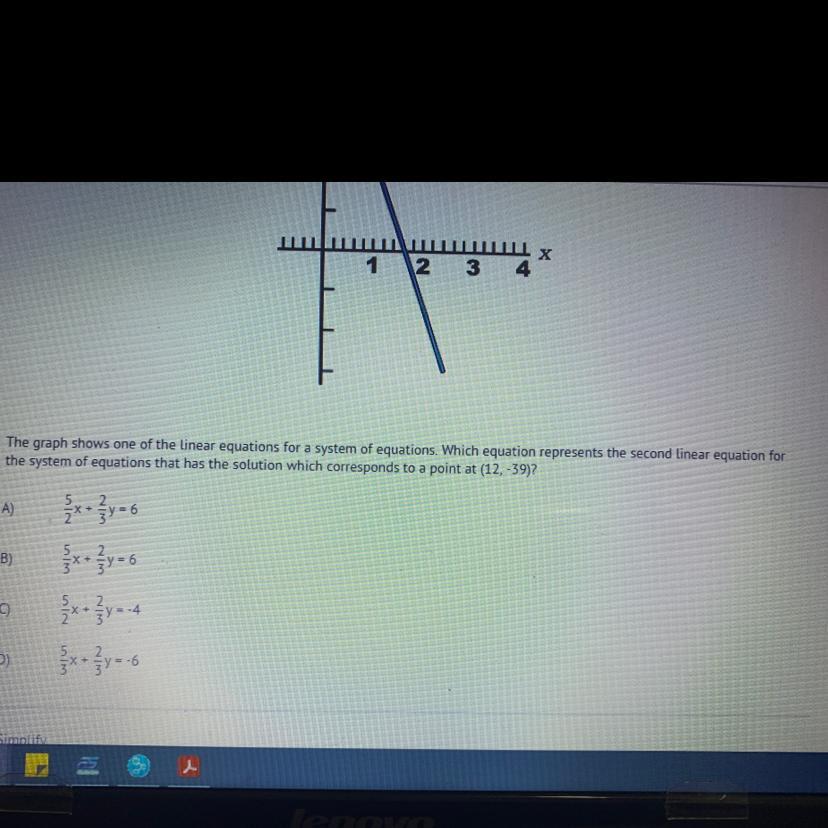
The graph shows one of the linear equations for a system of equations. Which equation represents the second linear equation for
the system of equations that has the solution which corresponds to a point at (12, -39)?

Answer:

Sine functions show repeated and periodic behavior. They are used to model wave-like behavior. They can be used to make predictions based on the model.

Step-by-step explanation:

I calculated it logically

Answer:

12

Step-by-step explanation:

Answer:

7

Step-by-step explanation:

Sub -1 in for each x:

-3x³-4x

-3(-1)³-4(-1)

-3(-1)+4

3+4

7

Answer:

1. 142 in.²

2. 190 cm²

Step-by-step explanation:

Both solids are rectangular prisms.

Surface area of a rectangular prism = 2(LW + LH + HW)

1. L = 7 in.

W = 3 in.

H = 5 in.

Plug ok the values into the formula

Surface area = 2(7*3 + 7*5 + 5*3)

= 142 in.²

2. L = 10 cm

W = 3 cm

H = 5 cm

Plug ok the values into the formula

Surface area = 2(10*3 + 10*5 + 5*3)

= 190 cm²

Answer:

The null hypothesis is [tex]H_0: p_1 - p_2 = 0[/tex]

The alternate hypothesis is [tex]H_a: p_1 - p_2 \neq 0[/tex]

The pvalue of the test is 0.03 < 0.05, which means that we have enough evidence to accept the alternative hypothesis that he proportion of people who wear life vests while riding a jet ski is not the same as the proportion of people who wear life vests while riding in a boat.

Step-by-step explanation:

Before testing the null hypothesis, we need to understand the Central Limit Theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean [tex]\mu[/tex] and standard deviation [tex]s = \frac{\sigma}{\sqrt{n}}[/tex].

For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean [tex]\mu = p[/tex] and standard deviation [tex]s = \sqrt{\frac{p(1-p)}{n}}[/tex]

Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

Out of 500 randomly selected people who rode a jet ski, 85% wore life vests.

This means that [tex]p_1 = 0.85, s_1 = \sqrt{\frac{0.85*0.15}{500}} = 0.016[/tex]

Out of 250 randomly selected boaters, 90.4% wore life vests.

This means that [tex]p_2 = 0.904, s_2 = \sqrt{\frac{{0.904*0.096}{250}} = 0.019[/tex]

Test the claim that the proportion of people who wear life vests while riding a jet ski is not the same as the proportion of people who wear life vests while riding in a boat.

At the null hypothesis, we test that the proportions are the same, that is, the subtraction between them is zero. So

[tex]H_0: p_1 - p_2 = 0[/tex]

At the alternate hypothesis, we test that the proportions are different, that is, the subtraction between them is different of zero. So

[tex]H_a: p_1 - p_2 \neq 0[/tex]

The test statistic is:

[tex]z = \frac{X - \mu}{s}[/tex]

In which X is the sample mean, [tex]\mu[/tex] is the value tested at the null hypothesis and s is the standard error.

0 is tested at the null hypothesis:

This means that [tex]\mu = 0[/tex]

From the two samples, we have that:

[tex]X = p_1 - p_2 = 0.85 - 0.904 = -0.054[/tex]

[tex]s = \sqrt{s_1^2+s_2^2} = \sqrt{0.016^2 + 0.019^2} = 0.0248[/tex]

Test statistic:

[tex]z = \frac{X - \mu}{s}[/tex]

[tex]z = \frac{-0.054 - 0}{0.0248}[/tex]

[tex]z = -2.17[/tex]

Pvalue of the test and decision:

The pvalue of the test is the probability that the difference differs from 0 by at least 0.054, which is P(|Z| > 2.17), which is 2 multiplied by the pvalue of z = -2.17

Looking at the z-table, z = -2.17 has a pvalue of 0.015

2*0.015 = 0.03

The pvalue of the test is 0.03 < 0.05, which means that we have enough evidence to accept the alternative hypothesis that he proportion of people who wear life vests while riding a jet ski is not the same as the proportion of people who wear life vests while riding in a boat.

Answer:

58 students

Step-by-step explanation:

Given

[tex]Total = 85[/tex]

[tex]French = 27[/tex]

[tex]Geometry = 51[/tex]

[tex]History = 38[/tex]

[tex]None = 5[/tex]

[tex]All = 2[/tex]

Required

Students that take only 1 subjects

The attached image illustrates the question.

For French only (x), we have:

[tex]x + 7 -2+10-2+2=27[/tex]

[tex]x + 15=27[/tex]

Collect like terms

[tex]x =- 15+27[/tex]

[tex]x =12[/tex]

For Geometry only (y), we have:

[tex]y+10-2+15-2+2=51[/tex]

[tex]y+23=51[/tex]

Collect like terms

[tex]y=-23+51[/tex]

[tex]y=28[/tex]

For History only (z), we have:

[tex]z +15-2+7-2+2=38[/tex]

[tex]z +20=38[/tex]

Collect like terms

[tex]z =-20+38[/tex]

[tex]z =18[/tex]

Students with one subject is then calculated as:

[tex]1\ subject = x+y+z[/tex]

[tex]1\ subject = 12 + 28 + 18[/tex]

[tex]1\ subject = 58[/tex]

Answer:

Give me a sec and ill answer in this comments k

Step-by-step explanation:

Answer:

the answer should be V = a³=2³=8cm³

Answer:

8cm

Step-by-step explanation:

The volume of a cube is length x width x height. If it a equal cube, all sides should be the same. Meaning that 2 x 2 x 2, equaling 8 would be the answer.

Answer:

a) The mean is 0.8.

b) The standard deviation is 0.0365.

c) Normal

Step-by-step explanation:

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean [tex]\mu[/tex] and standard deviation [tex]s = \frac{\sigma}{\sqrt{n}}[/tex].

For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean [tex]\mu = p[/tex] and standard deviation [tex]s = \sqrt{\frac{p(1-p)}{n}}[/tex]

80% of Americans over the age of 25 have earned a high school diploma.

This means that [tex]p = 0.8[/tex]

Suppose we take a random sample of 120 Americans

This means that [tex]n = 120[/tex].

Question a:

The mean is:

[tex]\mu = p = 0.8[/tex]

The mean is 0.8.

Question b:

The standard deviation is:

[tex]s = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0.8*0.2}{120}} = 0.0365[/tex]

The standard deviation is 0.0365.

Question c:

By the Central Limit Theorem, approximately normal.

a) The mean is 0.8.

b) The standard deviation is 0.0365.

c) Normal

Here, we have,

we know that,

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean x and standard deviation σ, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean x and standard deviation s = σ/√n .

For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean x=p and standard deviation s=√p(1-p)/n

80% of Americans over the age of 25 have earned a high school diploma.

This means that p=0.8

Suppose we take a random sample of 120 Americans

This means that n=120.

Question a:

The mean is:

x=p=0.8

The mean is 0.8.

Question b:

The standard deviation is:

s=0.0365

The standard deviation is 0.0365.

Question c:

By the Central Limit Theorem, approximately normal.

Learn more about standard deviation here:

brainly.com/question/23907081

#SPJ6

Answer:

x = 30°

x = 80°

Step-by-step explanation:

Recall: an inscribed angle is half the measure of the intercepted arc

Thus:

x = ½(arc cb)

Substitute

x = ½(60)

x = 30°

x = ½(arc ab)

Substitute

x = ½(160)

x = 80°

Answer:

Since the calculated value z= -1.956 does not lie in the critical region z= ± 1.96  we conclude that  true average hourly wage of a server is not different than the claim of $12.

Step-by-step explanation:

The null and alternate hypotheses are

H0: u= 12 against the claim Ha: u≠ 12

Taking significance level alpha = 0.05

The critical region is z= ± 1.96 for two tailed test

The sample size = n= 30

The sample mean = 11

Sample standard deviation= 2.80

Applying z- test

Z= x-u/s/√n

z= 11-12/2.8/√30

z= -1/0.5112

z= -1.956

Since the calculated value z= -1.956 does not lie in the critical region z= ± 1.96  we conclude that  true average hourly wage of a server is not different than the claim of $12.

Answer:

B

Step-by-step explanation:

9+9+6+6=18+12=30

hope it helps :)

Answer:

-3/4

Step-by-step explanation:

In slope-intercept form, the slope is the coefficient of x.

Answer:

90 degrees

Step-by-step explanation:

Answer:

Solution given.

f = 5, g = 6, h = 7

<F=?

we have;

f² = g² + h² – 2gh cos F

5²-6²-7²=-2×6×7 cos F

-60/-84=cos F

F=cos-¹(5/7)=44.41°

<F=44.4° is a required answer

Answer:

24

Step-by-step explanation:

I just did it in class. it was hard but you just have to think about the question

Answer:

G. 25%

Step-by-step explanation:

given : The price of a video game was reduced from $60 to $45 .

$60 - $45 = $15

then, the percentage was the price of the video game reduced :-

reduction in price/previous price x 100 = 15/60 x 100 = 25%

the percentage was the price of the video game reduced = 25%

Answer:

13 miles in feet = 68640 feet

we now need to get the number of cars, we use division to get groups

68640 / 15 = 4576.

we now see there are 4576 cars in the traffic jam.

Less, they are longer cars so the divosor would no longer be 15, it would be a higher number. 4576 cars would  not be able to fit in a 13 mile stretch if those cars were any longer.

Answer:

1/4

Step-by-step explanation:

1/2 x 1/2 = 1/4

Answer:

y=11/5x+1

Step-by-step explanation:

I am probably wrong :/

Answer:

y= -2/5x+1

Step-by-step explanation:

The slope of the line is -2/5 and the y intercept is 1.

Answer:

−60x + 135

Step-by-step explanation:

Answer:

150 - (0.4×150+15)

= 150-75

= 75

9514 1404 393

Answer:

  A.  7√3

Step-by-step explanation:

The side length ratios in a 30°-60°-90° triangle are 1 : √3 : 2. Here, the shortest side is 7, and x is the next-longer side.

  x = 7√3

Answer:

both outputs are x so f(x) and g(x) are inverses of each other

Step-by-step explanation:

Answer:

what are the options of answers?

Step-by-step explanation:

Answer:

All sides are the same length (congruent) and all interior angles are the same size (congruent). if Sqr refers to square

Answer:

91in^2

Step-by-step explanation:

SA of base =  7x7 = 49in^2

SA of each triangle = 1/2 x 7 x 3 = 10.5in^2

SA of all 4 triangles = 10.5 x 4 = 42in^2

SA Total = 49 + 42.= 91inch^2

Answer:

[tex]\sigma (y_1-y_2)=39[/tex]

Step-by-step explanation:

From the question we are told that:

Urn 1 :2 Red, 3 Yellow

Urn 2:3 Red, 7 Yellow

Sample 1 [tex]n_1=75\ balls[/tex]

Sample 2 [tex]n_2=100\ balls[/tex]

Generally the Probability of Red ball drawn is mathematically given by

For Urn 1

[tex]P(R)_1=\frac{2}{5}[/tex]

[tex]P(R)_1=0.4[/tex]

For Urn 2

[tex]P(R)_1=\frac{3}{10}[/tex]

[tex]P(R)_1=0.3[/tex]

Generally the equation for Variance of two independent variables [tex]\sigma (y_1-y_2)[/tex] is mathematically given by

 [tex]\sigma (y_1-y_2)=\sigma y_2 +(-1)^2 \sigma(x_1)[/tex]

    Where red balls drawn from both Urn is Modeled

    [tex]Urn_1\ is\ Modeled\ as (n_1=75,p_1=0.4)[/tex]

   [tex]Urn_2\ is\ Modeled\ as\ (n_2=100,p_2=0.3)[/tex]

 [tex]\sigma (y_1-y_2)=n_2 p_2(1_p_2)+n_1*p_1(1-p_1)[/tex]

 [tex]\sigma (y_1-y_2)=100*0.3(1-0.3)+75*0.4(1-0.4)[/tex]

 [tex]\sigma (y_1-y_2)=39[/tex]

Therefore the variance of the random variable defined as the number of red balls is

 [tex]\sigma (y_1-y_2)=39[/tex]

Answer:

32768

Step-by-step explanation:

Each question has 2 options.

On a true/false test with one question, there are 2¹, or 2 possible answers

On a test with 2 questions, there are 2², or 4 possible answers.

On a test with 3 questions, there are 2³, or 8 possible answers.

So, 2¹⁵ = 32768 possible ways.