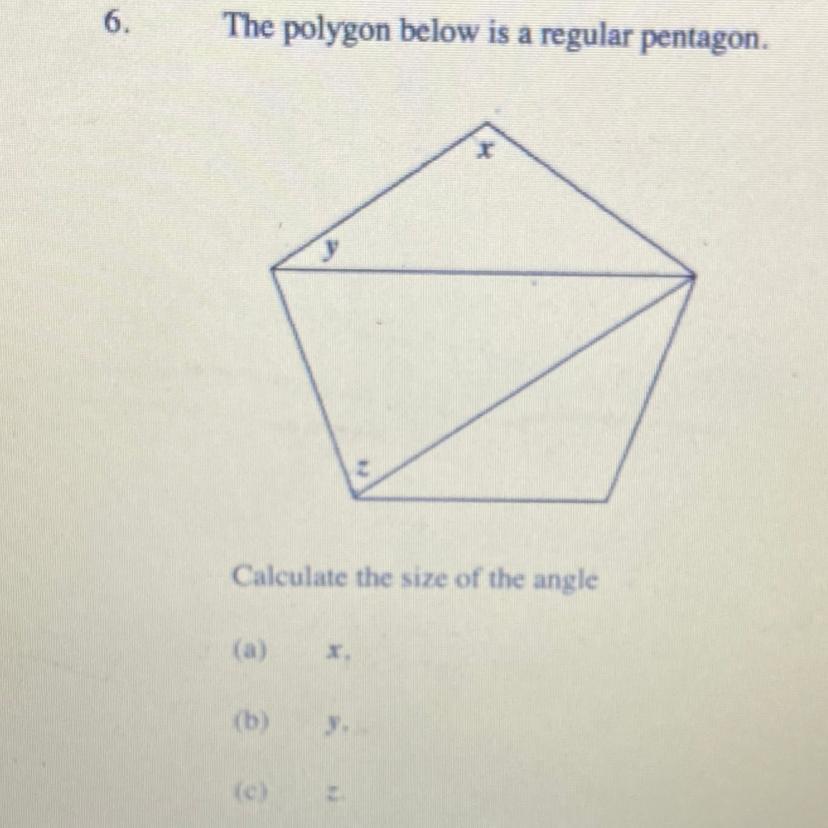
The polygon below is a regular pentagon.
Calculate the size of the angle
X
Y
Z
Answers
x = 108
y = 36
z = 72
=============================================================
Explanation:
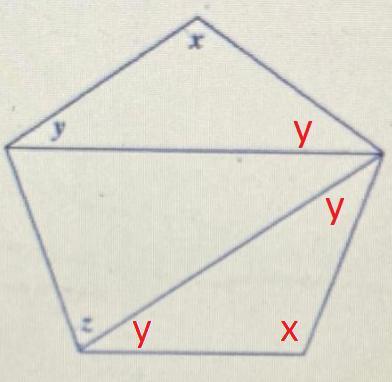
Check out the diagram below. I have added letters of x, y and z in places to help find the values of y and z. Note the triangle on top is isosceles (since a regular polygon has all sides equal; therefore the triangle on top has the top diagonal sides equal).
Before we find either y or z, let's find x.
For any regular polygon, the interior angles are all the same measure. They sum to 180(n-2). In this case, n = 5, so the angles sum to 180(5-2) = 540. Each individual interior angle is 540/n = 540/5 = 108 degrees
x = 108
Another way to find this interior angle is to first find the exterior angle. For any convex polygon (regular or not), the exterior angles always add to 360. When we talk about regular polygons, each individual exterior angle is 360/n. So in this case, we have 360/5 = 72 as one exterior angle. The adjacent interior angle is therefore x = 180-72 = 108. So there are two ways to find the measure of an interior angle.
--------
Referring to the diagram, specifically the isosceles triangle on top, we can see that it has angles of x, y and y. They add to x+y+y = x+2y. Set this equal to 180, plug in x = 108 and solve for y
x+2y = 180
108+2y = 180
2y = 180-108
2y = 72
y = 72/2
y = 36
--------
The bottom most triangle is a congruent copy of the triangle on top. We have another isosceles triangle with the same side lengths as before. This triangle also has x, y and y as mentioned above.
Notice the adjacent angles of y and z in the bottom left corner. They must add to 108 as this was the measure of the interior angle of a regular pentagon. So,
y+z = x
36+z = 108
z = 108-36
z = 72
Related Questions
Simplify the expression.
–6.5(–4.9)
Answers
Answer:
31.85
Step-by-step explanation:
Hey there!
Well to simplify the given expression we do,
-6.5 * -4.9
= 31.85
Hope this helps :)
Which is the simplified form of the expression ((2sqrt-2)(3sqrt4))sqrt-3 * ((2sqrt-3)(3sqrt2))sqrt2
Answers
Answer:
[tex]\boxed{-432\sqrt{2} i}[/tex]
Step-by-step explanation:
[tex]( 2 \sqrt{-2} )( 3 \sqrt{4} ) \sqrt{-3} \times ( 2 \sqrt{-3} )( 3 \sqrt{2} ) \sqrt{2}[/tex]
[tex]2 \times \sqrt{-2} \times 3 \times \sqrt{4} \times \sqrt{-3} \times 2 \times \sqrt{-3} \times 3 \times \sqrt{2} \times \sqrt{2}[/tex]
[tex]2 \times \sqrt{-2} \times 3 \times 2 \times \sqrt{-3} \times 2 \times \sqrt{-3} \times 3 \times 2[/tex]
[tex]2 \times \sqrt{-2} \times 3 \times 2 \times -3 \times 2 \times 3 \times 2[/tex]
[tex]-432\sqrt{2}\sqrt{-1}[/tex]
[tex]-432\sqrt{2} i[/tex]
Answer: it’s d!
Step-by-step explanation:
A right-angled triangle has shorter side lengths exactly c^2-b^2 and 2bc units respectively, where b and c are positive real numbers such that cc is greater than b. Find an exact expression for the length of the hypotenuse (in appropriate units).
Answers
Answer: hypotenuse = [tex]c^{2} + b^{2}[/tex]
Step-by-step explanation: Pythagorean theorem states that square of hypotenuse (h) equals the sum of squares of each side ([tex]s_{1},s_{2}[/tex]) of the right triangle, .i.e.:
[tex]h^{2} = s_{1}^{2} + s_{2}^{2}[/tex]
In this question:
[tex]s_{1}[/tex] = [tex]c^{2}-b^{2}[/tex]
[tex]s_{2} =[/tex] 2bc
Substituing and taking square root to find hypotenuse:
[tex]h=\sqrt{(c^{2}-b^{2})^{2}+(2bc)^{2}}[/tex]
Calculating:
[tex]h=\sqrt{c^{4}+b^{4}-2b^{2}c^{2}+(4b^{2}c^{2})}[/tex]
[tex]h=\sqrt{c^{4}+b^{4}+2b^{2}c^{2}}[/tex]
[tex]c^{4}+b^{4}+2b^{2}c^{2}[/tex] = [tex](c^{2}+b^{2})^{2}[/tex], then:
[tex]h=\sqrt{(c^{2}+b^{2})^{2}}[/tex]
[tex]h=(c^{2}+b^{2})[/tex]
Hypotenuse for the right-angled triangle is [tex]h=(c^{2}+b^{2})[/tex] units
The expression for the length of the hypotenuse is [tex]c^2+ b^2 \ units[/tex].
Given that,
A right-angled triangle has shorter side lengths exactly [tex]c^{2} - b^{2}[/tex] and 2bc units respectively,
Where b and c are positive real numbers such that c is greater than b.
We have to determine,
An exact expression for the length of the hypotenuse?
According to the question,
The Pythagoras theorem states that the sum of the hypotenuse in the right-angled triangle is equal to the sum of the square of the other two sides.
A right-angled triangle has shorter side lengths exactly [tex]c^{2} - b^{2}[/tex] and 2bc units respectively,
Where b and c are positive real numbers such that c is greater than b.
Therefore,
The expression for the length of the hypotenuse is,
[tex]\rm (Hypotenuse)^2 = (c^2-b^2)^2+ (2bc)^2\\\\(Hypotenuse)^2 = c^4+ b^4 - 2c^2b^2 + 4c^2b^2\\\\(Hypotenuse)^2 = c^4+ b^4 +2c^2b^2 \\\\Hypotenuse = \sqrt{c^4+ b^4 +2c^2b^2}\\\\\ Hypotenuse = \sqrt{(c^2+ b^2)^2}\\\\ Hypotenuse = c^2+b^2 \ units[/tex]
Hence, The required expression for the length of the hypotenuse is [tex]c^2+ b^2 \ units[/tex].
For more details refer to the link.
https://brainly.com/question/9214495
HELPP PLEASE
2. At Math Camp, students can either pack their own lunch every day or buy lunch at camp. If they want to buy lunch there are 3 options: Option A: they pay an initial fee of $30 and lunches cost $2 each Option B: shown on the graph Option C: they pay a flat fee of $70 which includes all lunches Write an equation for each option. (3 marks) Option A: Option B: Option C: b) Describe under what conditions, a student should choose each option. (Hint: you may want to graph all 3 lines on the same axes) (4 marks) Choose Option A if: Choose Option B if: Choose Option C if: 3. 4. A Campbell’s Soup can is 15cm tall and has a radius of 5 cm. How much paper is needed to make the label (think about what the label covers)? (3 marks) How much soup can this hold? (1 cm3 = 1 mL) (3 marks)
Answers
Answer:
3.
A. Y = 2x + 30 (red line)
B. Y=5x (blue line)
C. Y=70 (green line)
From 0 to 10 days, choose option B (shown on graph)
From 10 to 20 days, choose option A (first option)
From 20 days and more, choose option C.
4.
surface area of label = 471.2 cm^2
Step-by-step explanation:
Q1718436 Math Camp
2. At Math Camp, students can either pack their own lunch every day or buy lunch at camp. If they want to buy lunch there are 3 options:
Option A: they pay an initial fee of $30 and lunches cost $2 each
Option B: shown on the graph
Option C: they pay a flat fee of $70 which includes all lunches
Write an equation for each option. (3 marks) Option A: Option B: Option C:
A. Y = 2x + 30 (red line)
B. Y=5x (blue line)
C. Y=70 (green line)
b) Describe under what conditions, a student should choose each option. (Hint: you may want to graph all 3 lines on the same axes) (4 marks)
Choose Option A if: Choose Option B if: Choose Option C if:
Least cost is what is below the lowest possible line for the number of days stayed.
From 0 to 10 days, choose option B (shown on graph)
From 10 to 20 days, choose option A (first option)
From 20 days and more, choose option C.
Note that for days 10 and 20, there are two choices each.
3.
4. A Campbell’s Soup can is 15cm tall and has a radius of 5 cm. How much paper is needed to make the label (think about what the label covers)? (3 marks) How much soup can this hold? (1 cm3 = 1 mL) (3 marks)
The label only covers the curved surface.
Curved surface area
= 2 pi * r * h
= 2 pi (5) * 15
= 150 pi
= 471.2 cm^2
Rearrange the following formula to solve for p: wa+3p=q
Answers
Answer:
wa + 3p = q
3p = q - wa -- Subtract wa
p = (q - wa) / 3 -- Divide by 3
Answer:
[tex] \boxed{\sf p = \frac{1}{3} (p - wa)} [/tex]
Step-by-step explanation:
[tex] \sf Solve \: for \: p: \\ \sf \implies wa + 3p = q \\ \\ \sf Subtract \: wa \: from \: both \: sides: \\ \sf 3p = q - wa \\ \\ \sf Divide \: both \: sides \: by \: 3: \\ \sf \implies p = \frac{1}{3} (q- wa)[/tex]
What is the quotient (2x^3 + 3x - 22) / (x-2)
Answers
Answer:
The quotient is 2x^2+4x+11
Step-by-step explanation:
please help me answer this question Solve: y − x = 12 y + x = -26 (19, -7). (-7, 1). (7, 19). (-19, -7).
Answers
Answer:
(-19 , -7)
Step-by-step explanation:
y - x = 12
y + x = -25 we sum them to get
2y = -14 , y = -7
then we put -7 instead of y in any of the equations:
-7 - x = 12
-x = 19
x = -19,
finally (x , y) is (-19 , -7)
a map is drawn to a scale of 1 cm to 250 cm.
(a) an airport has an area of 240 cm² on the map. find its actual area in km².
Answers
Answer:
0.0015 km².
Step-by-step explanation:
It is given that a map is drawn to a scale of 1 cm to 250 cm.
[tex]1\ cm\times 1\ cm=250\ cm\times 250\ cm[/tex]
[tex]1\ cm^2=62500\ cm^2[/tex]
It is given that an airport has an area of 240 cm² on the map. So, its actual area is
[tex]Area=240\times 62500\ cm^2[/tex]
[tex]Area=15000000\ cm^2[/tex]
[tex]Area=\dfrac{15000000}{10000000000}\ km^2[/tex]
[tex]Area=0.0015\ cm^2[/tex] [tex][\because 1\ km^2=10000000000\ cm^2][/tex]
Therefore, the area of airport is 0.0015 km².
The third, fifth and eighth terms of an AP are the first 3 consecutive terms of a GP. Given that the first term of the AP is 8, calculate the common difference
Answers
Answer:
The common difference = 2.
Step-by-step explanation:
An AP can be written as a1, a1 + d, a1 + 2d, a1 + 3d, a1 + 4d, a1 + 5d, a1 + 6d , a1 + 7d.
where a1 = first term and d is the common difference.
Here first term = a1 = 8
3rd term = a1 + 2d = 8 + 2d
5th term = a1 + 4d = 8 + 4d
8th term = 8 + 7d
First 3 terms of a GP are a , ar and ar^2
So from the given information:
a = 8 + 2d
ar = 8 + 4d
ar^2= 8 + 7d
Dividing the second equation by the first we have
r = (8 + 4d)/(8 + 2d)
Dividing the third by the second:
r = (8 + 7d) / (8 + 4d)
Therefore, eliminating r we have:
(8 + 4d)/(8 + 2d) = (8 + 7d)/(8 + 4d)
(8 + 4d)^2 = (8 + 2d)(8 + 7d)
64 + 64d + 16d^2 = 64 + 72d^ + 14d^2
2d^2 - 8d = 0
2d(d^2 - 4) = 0
2d = 0 or d^2 = 4, so
d = 0, 2.
The common difference can't be zero so it must be 2.
Trigonometry.... plzzz helllppp
Answers
Answer:
Hey there!
We can write this equation:
cosine xyz=6/15, or 0.4
arc cosine 0.4= 66.4
Thus, angle xyz is 66.4 degrees
Hope this helps :)
Please help. I will give out brainliest
Answers
Answer:
the table is correct
the graph will look like:
Martin will earn $25 per hour at a new job. During training, he will earn $20 per hour. What percent of Martin's regular hourly rate will he earn during training?
Answers
Answer:
He will earn 80% during training
Step-by-step explanation:
Lets take $25 as 100%
And take $20 as x
Using equivalent ratios, the equation would look like: $25:100% = $20:x
Next, turn them into fractions: $25 = $20
100% x
Cross multiply to get:
(25)x = $20×100%
The next step:
25x = $20×100%
25 25
25 and 25 will cancel each other out leaving x, and 25 will divide 100% which will give you 4
Leaving it as:
x= 20×4%
x= 80%
Which is the graph of f(x) = /x?
Answers
Answer:
neither on of those. I can't see the the other answers so your best bet is to look on m-a-t-h-w-a-y. (had to spell out with hyphens but remove them and go to that)
Step-by-step explanation:
Find the vertex form
Answers
Hi,
[tex]y=5x^{2} +12x-2\\y=x(5x+12)-\frac{46}{5} \\y=5(x+\frac{6}{5} )^{2}-\frac{46}{5} \\[/tex]
Have a good day.
Samuel is solving the equation 3 (x minus 1) + 4 = 2 minus (x + 3). Which equivalent equations might Samuel use? Check all that apply.
3 x minus 3 + 4 = 2 minus x minus 3
3 x minus 1 + 4 = 2 minus x + 3
3 x minus 3 + 4 = 2 minus x + 3
3 x + 1 = negative x minus 1
3 x + 3 = negative x + 5
3 x + 1 = negative x + 5
Answers
Answer: 3 x minus 3 + 4 = 2 minus x minus 3
3 x + 1 = negative x minus 1
Step-by-step explanation:
A and D. Edge 2020
The required equation that Samuel used is 3x -3 + 4 =2- x -3. option A is correct.
Samuel is solving the equation 3 (x minus 1) + 4 = 2 minus (x + 3). Which equivalent equations might Samuel use, is to be determined.
The equation is the relationship between variables and represented as[tex]y = ax +b[/tex] is an example of a polynomial equation.
Given equation is [tex]3(x-1) +4 =2 -(x+3)[/tex]
Simplification of the above equation,
opening the parenthesis on both sides
step 1⇒ 3x - 3 + 4 = 2 - x - 3
step 2⇒ 3x + 1 = -x - 1
Transposition of -x to the left side and +1 to the right side
step 4 ⇒ 3x +x = -1 -1
4x = -2
Transposition of 4 to the denominator of -2.
step 5⇒ x = -2/4
x = -1/2
Thus , Step 1 3x -3 + 4 =2- x -3 is the equivalent equation used by the samuel.
Learn more about the equation here:
brainly.com/question/10413253
#SPJ5
need HELP ON THIS A S AP !!!!!
Answers
Answer:
803.84yd²
Step-by-step explanation:
Surface Area of A Sphere: [tex]A=4\pi r^2[/tex]
We are given the radius of 8 yards.
Using 3.14 for pi:
[tex]A=4*3.14*8^2\\\\A=4*3.14*64\\\\A=12.56*64\\\\\boxed{A=803.84}[/tex]
The correct answer should be 803.84yd².
Brainilest Appreciated.
Answer:
803.84 yd^2
Step-by-step explanation:
4*3.14*8^2
12.56*64
803.84
brainliest pls
hope i helped
-ZYLYNN
in how many ways can you select a committee of 3 students out of 10 students ?
Answers
The registrar keeps an alphabetical list of all undergraduates, with their current addresses. Suppose there are 10,000 undergraduates in the current term. Someone proposes to choose a number at random from 1 to 100, count that far down the list, taking that name and every 100th name after it for the sample.
a) Is this a probability method?
b) Is it the same as simple random sampling?
c) Is there selection bias in this method of drawing a sample?
Answers
Answer:
The answer to this question can be defined as follows:
Step-by-step explanation:
Following are the description of the given points:
(a) This is a system of probability, which possibility occurs inside an intended manner whenever they choose this specific point of origin from 1 to 100 with no one reserve the possibility about who gets throughout the survey.
(b) Its method is different from the random sampling technique with the base available. For example, two individuals whose names identical to both the list have no chance to join within the survey.
(c) its sample is objective to its everyone can enter the test in equal measure.
Miguel is playing a game in which a box contains four chips with numbers written on them. Two of the chips have the number 1, one chip has the number 3, and the other chip has the number 5. Miguel must choose two chips, and if both chips have the same number, he wins $2. If the two chips he chooses have different numbers, he loses $1 (–$1).
Let X = the amount of money Miguel will receive or owe. Fill out the missing values in the table. (Hint: The total possible outcomes are six because there are four chips and you are choosing two of them.)
Answers
Answer:
[tex]P(X_i=2) =\dfrac{1}{6}[/tex]
[tex]P(X_i=-1) =\dfrac{5}{6}[/tex]
Step-by-step explanation:
Given the numbers on the chips = 1, 1, 3 and 5
Miguel chooses two chips.
Condition of winning: Both the chips are same i.e. 1 and 1 are chosen.
Miguel gets $2 on winning and loses $1 on getting different numbers.
To find:
Probability of winning $2 and losing $1 respectively.
Solution:
Here, we are given 4 numbers 1, 1, 3 and 5 out of which 2 numbers are to be chosen.
This is a simple selection problem.
The total number of ways of selecting r numbers from n is given as:
[tex]_nC_r = \frac{n!}{r!(n-r)!}[/tex]
Here, n = 4 and r = 2.
So, total number of ways = [tex]_4C_2 = \frac{4!}{2!\times 2!} = 6[/tex]
Total number of favorable cases in winning = choosing two 1's from two 1's i.e. [tex]_2C_2 = \frac{2!}{2! 0! } = 1[/tex]
Now, let us have a look at the formula of probability of an event E:
[tex]P(E) = \dfrac{\text{Number of favorable ways}}{\text{Total number of ways}}[/tex]
So, the probability of winning.
[tex]P(X_i=2) =\dfrac{1}{6}[/tex]
Total number of favorable cases for -1: (6-1) = 5
So, probability of getting -1:
[tex]P(X_i=-1) =\dfrac{5}{6}[/tex]
Please refer to the attached image for answer table.
Answer:
two = 1/6
and -1 = 5/6
Step-by-step explanation:
Can y’all solve this for me???
Answers
Answer:
1/4PI I GOT IT RIGHT ON KHAN ACADEMY
Step-by-step explanation:
HOPE I HELPED
PLS MARK BRAINLIEST
DESPERATELY TRYING TO LEVEL UP
✌ -ZYLYNN JADE ARDENNE
Answer:
[tex]\boxed{\frac{1}{2}\pi}[/tex]
Step-by-step explanation:
Use length of arc formula.
[tex]\frac{\theta }{360} \times2 \pi r[/tex]
The radius is 1 unit.
θ = 90°
[tex]\frac{90}{360} \times 2\pi (1)[/tex]
[tex]\frac{1}{4} \times 2\pi[/tex]
[tex]\frac{1}{2} \times\pi[/tex]
Which of the following are identities? Check all that apply.
Answers
Answer:
The true answers:
A
B
C
Step-by-step explanation:
A P E X
Please help ASAP! If correct will mark brainliest
Answers
Answer:
5
Step-by-step explanation:
We need to find the value of AP
First, lets compare the perimeters:
P_ABC= AB+BC+AC= 45P_ABP= AB+BP+AP = 25P_APC= AP+AC+PC= 30Sum of the perimeters of smaller triangles:
P_ABP+P_APC= AB+BP+AP+ AP+AC+PCAs BP+PC= BC we can put it as:
AB + BC +AC + 2APand
P_ABC+2APPlug in values of perimeters:
25+30= 45+ 2AP2AP= 10AP= 10/2AP= 5Answer is: 5
HELP ASAP WILL MARK BRAINLIEST
Answers
Answer:
4 hours
Step-by-step explanation:
Formula for volume of a cylinder is πr² · h
1. Find the volume of the pool
π(3.5²) · 1.9 = 73.1 m³
2. Divide by the amount of water pumped out per hour (17 m³)
73.1 ÷ 17 = 4.3
It would take 5 hours to completely empty the pool but 4.3 rounded to the nearest whole hour is 4 hours.
Answer:
The hours does it take to empty the pool is 4.299
Step-by-step explanation:
In order to calculate how many hours does it take to empty the pool, we would have to make the following calculation:
hours does it take to empty the pool=Volume of cylinder/rate water is pumped out of the pool
rate water is pumped out of the pool=17m∧3
Volume of cylinder=pi*r∧2*l
According to the given data:
r=3.5
l=1.9
Therefore, Volume of cylinder=3.14*3.5∧2*1.9
Volume of cylinder=73.0835 m∧3
hours does it take to empty the pool=73.0835/17
hours does it take to empty the pool=4.299
The hours does it take to empty the pool is 4.299
Se tiene una pirámide regular cuadrangular cuyas caras laterales forman con la base un angulo que mide 53º y el area de la superficie lateral es 60 ¿cuanto mide la altura?
Answers
Answer:
La altura de la pirámide es de 8.14 unidades.
Step-by-step explanation:
Hay una pirámide cuadrangular regular cuyas caras laterales forman un ángulo que mide 53º con la base y el área de la superficie lateral es 60. ¿Qué altura tiene?
Dado que el área de superficie lateral = 60
Tenemos
Área del triángulo equilátero = (√3 / 4) × a²
(√3 / 4) × a² = 60
a² = 60 / (√3 / 4) = 80 · √3
a = √ (80 · √3) = 11.77 unidades
La altura inclinada = Altura de la superficie inclinada = a × sin (60) = 11.77 × sin (60)
La altura inclinada = 11.77 × sin (60) = 10.194 unidades
La altura de la pirámide = Altura inclinada × sin (ángulo de caras laterales con la base)
La altura de la pirámide = 10.194 × sin (53) = 8.14 unidades.
La altura de la pirámide = 8.14 unidades.
Evaluate m²p - p (m - p ) if m= 3 and p = 5
Answers
Answer:
55
Step-by-step explanation:
m^2p - p(m - p), if m=3 and p=5.
So we plug those value into the correct space...
(3)^2 (5) - (5) (3 - 5)
9x5 - 5 x (-2)
45 - (-10)
45 + 10
55
An icicle is in the shape of an inverted cone with a diameter of 14 mm and a height of 60 mm. How much frozen water
is in the icicle? Use 3.14 for Round the answer to the nearest tenth
A 188.4 mm
B 980.0 mm
C 3,077.2 mm
D 9,231.6 mm
Answers
Answer:
Option C. 3077.2 mm³
Step-by-step explanation:
Data obtained from the question include the following:
Diameter (d) = 17 mm
Height (h) = 60 mm
Pi (π) = 3.14
Volume =?
Next, we shall determine the radius of the cone. This is illustrated below:
Diameter (d) = 17 mm
Radius (r) =.?
Radius (r) = diameter (d)/2
r = d/2
r = 14/2
r = 7 mm.
The radius therefore, is 7 mm.
To know how much frozen water
is in the icicle, we shall calculate the volume of the icicle using the formula for calculating the volume of a cone. This is illustrated below:
Height (h) = 60 mm
Pi (π) = 3.14
Radius (r) = 7 mm
Volume =..?
V = ⅓πr²h
V = ⅓ × 3.14 × 7² × 60
V = 3.14 × 49 × 20
V = 3077.2 mm³
Therefore, the amount of frozen water in the icicle is 3077.2 mm³
Answer:
C 3,077.2 mm
Step-by-step explanation:
Add the polynomial
(6s3+9s+10)and(3s3+4s-10)
PLEASE HELP!!! ASAP!!!
Answers
Answer:
9s³ ⁺ 13sStep-by-step explanation:
6s³ + 9s + 10 + 3s³ + 4s - 10
Collect like terms
6s³ + 3s³ + 9s + 4s + 10 - 10
Since, two opposites add up to zero, remove them from the expression
6s³ + 3s³ + 9s + 4s
add the like terms
9s³ + 13s
hope this helps..
best regards!!
Answer:
9s^3+13s
Step-by-step explanation:
Add each term:
9s^3+13s
I hope this helps...
And plz mark me brainliest!!
Pam works as an office administrator. She spends $7500 of her income on personal expenses each year. If this represents 18% of her salary, how much money does Pam earn in one year? Round your answer to the nearest whole dollar.
Answers
Answer:
Her annual salary is approximately $41,667
Step-by-step explanation:
Hello,
This question deals with percentage of a number and it's very easy :)
First of all, get the data and understand what's required of us.
Pam spends $7500 yearly on expenses
But this amount represents 18% of her annual income.
Let her annual income be represented by x
18% = 7500 / x
18÷100 = 7500÷x
cross multiply and solve for x
18 × x = 7500 × 100
18x = 750,000
divide both sides by 18
18x / 18 = 750,000 / 18
x = $41,666.67
x = $41,667
Her annual salary is approximately $41,667
after allowing 20%discount on the m.p of a mobile,15% vat was levied and sold it.If the differences between selling price with vat and selling price after discount is rs.1800,find the marked price of the mobile
Answers
Answer:
Market price = Rs. 15,000
Step-by-step explanation:
Let Market price = x
discount = 20% of x
= 0.20 *x = 0.2x
Selling price after discount = x - 0.2x = 0.8x
Value added tax = 15% of 0.8x
= 0.15 * 0.8x
= 0.12x
Selling price with VAT = 0.8x + 0.12x = 0.92x
Differences between SP with vat and SP after discount = rs.1800
0.92x - 0.8x = 1800
0.12 x = 1800
x = 1800/0.12
x = Rs. 15,000
V2=u2+2as v 2 = u 2 + 2 a s Where v v is the final velocity (in m/s), u u is the initial velocity (in m/s), a a is the acceleration (in m/s²) and s s is the distance (in meters). Find v v when u u is 9 m/s, a a is 7 m/s², and s s is 28 meters.
Answers
Answer:
Final velocity, v = 21.75 m/s
Step-by-step explanation:
Given that the relation between final velocity, initial velocity, acceleration and distance traveled is expressed as:
[tex]v^2=u^2+2as[/tex]
Also, given that:
Initial velocity, u = 9 m/s
Acceleration, a = 7 m/[tex]s^2[/tex]
Distance, s = 28 m
To find:
Final velocity, v = ?
Solution:
The given relation between v, u, a and s is:
[tex]v^2=u^2+2as[/tex]
We have the values of initial velocity, acceleration and distance traveled in the question statement. We just need to put all these values to find the value of final velocity.
Let us put all the values in the given equation and try to find final velocity, v:
[tex]v^2=9^2+2\times 7 \times 28\\\Rightarrow v^2=81+14 \times 28\\\Rightarrow v^2=81+392\\\Rightarrow v^2=473\\\Rightarrow v=\sqrt{473}\\\Rightarrow v=21.75\ m/s[/tex]
So, the answer is:
final velocity, v = 21.75 m/s