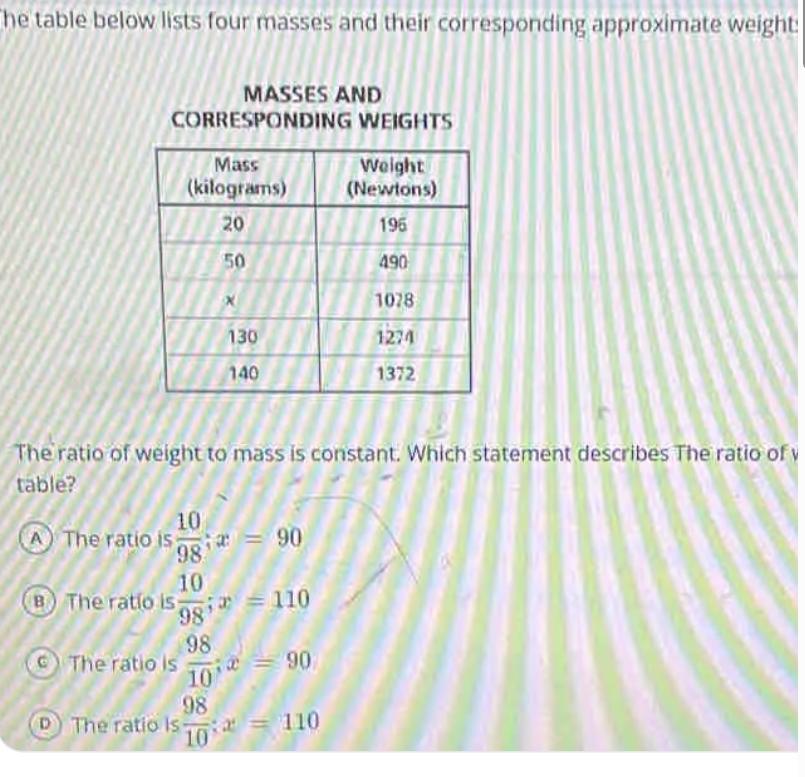
The ratio of the weight to the mass is constant. Which statement describes the ratio of the weight to the mass and the value of x in the table?

Answer: Yes

Step-by-step explanation: SSS criteria

Answer:

  A (top)

Step-by-step explanation:

You want to know which box plot represents the data in the given list.

The difference between the box plots is the location of the median.

When the data is sorted into order, it is ...

  {2500, 2712, 3500, 3876, 4247, 4753, 4983, 5000, 6214, 7500}

There are an even number of elements in this list, so the median is the average of the middle two:

  median = (4247 +4753)/2 = 9000/2 = 4500

The median is represented by the line inside the box of the box plot. The plot with its median at 4500 is the top one (shown in the attachment).

The top box plot represents the data.

<95141404393>

Answer:

Step-by-step explanation:

You want to identify the lines among those listed that will intersect the line y = 4.

The line y = 4 is a horizontal line. Any line of the form y = c, for some constant c (not 4), will be parallel and will not intersect y = 4.

All of the other lines listed will intersect y = 4.

The intersecting lines are ...

<95141404393>

we use linear equation in one variable to solve the problem. Kiran swam 10 laps in the pool.

Let's represent the number of laps Kiran swam as "z".

We know that Clare swam 18 laps, which is 9/5 times as many laps as Kiran. We can represent this relationship with the following equation:

18 = (9/5)z

To solve for z, we can isolate it by multiplying both sides of the equation by the reciprocal of 9/5, which is 5/9:

18 * (5/9) = (9/5)z * (5/9)

10 = z

Therefore, Kiran swam 10 laps in the pool.

To know more about linear equation in one variable Visit:

https://brainly.com/question/31529190

#SPJ1

The length of the lake in miles for the given situation of travelling motor boat is equal to 9 miles.

Let us consider the length of the lake be d in miles.

Number of miles motor boat travelled per hour = 18 miles

When the motor boat travels at 18 miles per hour,

The time it takes to travel the length of the lake is,

t₁ = d/18

When the motor boat travels at 12 miles per hour,

The time it takes to travel the length of the lake is,

t₂ = d/12

Time it takes to travel the length of the lake at 18 miles per hour

=  one-quarter of an hour less than the time it takes at 12 miles per hour,

⇒ t₁ = t₂ - 1/4

Substituting the expressions for t₁ and t₂ from above, we get,

⇒ d/18 = d/12 - 1/4

Simplify this equation by multiplying both sides by the least common multiple of the denominators,

least common multiple = 36

⇒ 2d = 3d - 9

Solving for d, we get,

⇒ d = 9

Therefore, the length in miles of the lake is 9 miles.

learn more about miles here

brainly.com/question/29173795

#SPJ4

As per the data mentioned in the table, Jade's mom is 0.7 ft or 1 ft taller than jade.

Mixed numbers represent whole numbers and proper fractions together. Usually represents a number between any two integers. Hybrid numbers are made by combining three parts:

An integer, a numerator, and a denominator. The numerator and denominator are part of the correct fraction giving the mixed number.

Height of jade's mom = 5⁵/₈ ft

Jade's height = 4⁵/₆

The difference in their heights is:

= (45/8) - (29/6)

= (270 - 232)/48

= 38/48

= 0.7 ft

0.7 ft ≈ 1 ft

To know more about mixed fractions, visit:

https://brainly.com/question/28999351

#SPJ1

List orders the times from shortest to longest

5 1/3 seconds

5 1/2 seconds

5 5/9 seconds

A decimal is a way of representing numbers using a base-10 positional notation system, where each digit represents a power of 10. It is written as a whole number followed by a decimal point and a series of digits representing fractions of 1.

According to the given information:

To order the times from shortest to longest, we need to convert them into a common format, such as a decimal or a common denominator.

First, let's convert the times to a common denominator of 9:

5 1/3 seconds = 16/3 seconds = 48/9 seconds

5 5/9 seconds = 50/9 seconds

5 1/2 seconds = 9/2 seconds = 45/9 seconds

Now we can order the times from shortest to longest:

48/9 seconds = 5 1/3 seconds

45/9 seconds = 5 1/2 seconds

50/9 seconds = 5 5/9 seconds

Therefore, the correct list in order from shortest to longest is:

5 1/3 seconds

5 1/2 seconds

5 5/9 seconds

So Bernard's first attempt was the shortest, his third attempt was the second longest, and his second attempt was the longest.

To know more about Decimal visit :

https://brainly.com/question/30958821

#SPJ1

Answer:

c.

Step-by-step explanation:

The original triangle has two sides with length 4x each, and the hypotenuse has length 3y.

After the enlargement, each of the sides with length 4x becomes 3y × 4x = 12xy, and the hypotenuse becomes 3y × 3y = 9y^2.

Therefore, the perimeter of the enlarged triangle is the sum of the lengths of its three sides:

12xy + 12xy + 9y^2 = 24xy + 9y^2 = 9y^2 + 24xy

So the answer is (C) 9y^2 + 24xy.

Hence, it is expected that 14 flights will arrive on time out of the 100 trials of this experiment.

The probability of an occurrence is a number used in mathematics to describe how likely it is that the event will take place. In terms of percentage notation, between 0% and 100% it is expressed as a number between 0 and 1, or . The higher the likelihood, the more likely it is that the event will take place.

 when we refer to an experiment or trial, we mean a random experiment. When difference  between a trial and an experiment, think of the experiment as a larger entity created by the fusion of several trials.

Unless otherwise stated,A trial is any specific outcome of a random experiment. In other words, a trial of the experiment is what we call when we conduct an experiment.

according to question, the number of on-time flights in 100 trials as a binomial random variable with parameters n = 100 (the number of trials) and p (the chance of success, i.e., a flight being on time), presuming that the probability of a flight being on time is the same in all trials.

The expected number of on-time flights in 100 trials is E(X) = np if the same of a flight being on time is p. Given that E(X) = 15, we determine p ,

E(X) = n p = 15 n = 100

p = [tex]\frac{E(X)}{n} = \frac{15}{100}[/tex] = 0.15

Therefore, it is probability that 0.15 %of flights will arrive on time.

To determine the expected  number of trials from a total of 100

Using the probability mass function of the binomial distribution, we can get the expected probability of trials out of 100 that result in precisely 15 flights departing on time:

[tex]P(X = 15)=(100 choose 15) * 0.15^{15} * 0.85^{85}[/tex]

We can calculate this 0.144 get  using a calculator.

therefore it is expected that 14 flights will arrive on time out of the 100 trials of this experiment. It should be noted that while this is an expected value, random fluctuation may cause the actual number of on-time flights in each trial to deviate somewhat from this figure.

Learn more about Probability here:

https://brainly.com/question/13604758

#SPJ1

Step-by-step explanation:

the equation for the following graph os (-3,-5) & (1,1)

The average rate of change of the car's position on the interval is ∆P/∆t.

To find the average rate of change of the car's position on the interval, follow these steps:

Identify the interval: First, determine the specific interval for which you need to find the average rate of change (e.g.,

between times t1 and t2).

Calculate the change in position:

Determine the car's position at both the beginning and end of the interval (e.g., positions P1 and P2).

Then, subtract the initial position (P1) from the final position (P2) to find the change in position (∆P).

Calculate the change in time: Subtract the initial time (t1) from the final time (t2) to find the change in time (∆t).

Calculate the average rate of change: Divide the change in position (∆P) by the change in time (∆t) to find the average

rate of change.

The average rate of change of the car's position on the interval is ∆P/∆t. Include units in your answer (e.g., meters per

second or miles per hour) to indicate the car's rate of change in position.

for such more question on average

https://brainly.com/question/20118982

#SPJ11

The choice of measures of center and variability depends on the shape and characteristics of the distribution. If the distribution is skewed or has outliers, then the median and IQR would be more appropriate measures of center and variability, respectively.

The median is a measure of central tendency that represents the middle value in a dataset when the data is arranged in order of magnitude. Specifically, it is the value that separates the data set into two equal halves. In other words, half of the values in the dataset are greater than the median, and the other half are less than the median.

To calculate the median, you first need to arrange the data in order from lowest to highest (or highest to lowest).

The value that divides the data set into two equal portions is called the median. It is a robust measure of center, meaning that it is not affected by extreme values or outliers. The IQR is the range of values that contains the middle 50% of the data, and it is also a robust measure of variability.

To know more about median, visit:

https://brainly.com/question/28060453

#SPJ1

as you already know, to get the inverse of any expression we start off by doing a quick switcheroo on the variables and then solving for "y", let's do so for this inverse, since finding the inverse of the inverse, will give us the original function :)

[tex]f^{-1}(x)=-3x+2\implies y~~ = ~~-3x+2\hspace{5em}\stackrel{\textit{quick switcheroo}}{x~~ = ~~-3y+2} \\\\\\ x-2=-3y\implies \cfrac{x-2}{-3}=y\implies \cfrac{2-x}{3}=y=f(x)[/tex]

The probability that you rolled a 5, given that the number rolled was greater than 3, is 1/3 or approximately 0.333.

We need to find the probability that you rolled a 5, given that the number rolled was greater than 3. Let's break this down step by step:

1. Identify the total number of outcomes: Since it is a 6-sided dice, there are 6 possible outcomes (1, 2, 3, 4, 5, and 6).

2. Determine the number of outcomes greater than 3: The outcomes greater than 3 are 4, 5, and 6. There are 3 possible outcomes that satisfy this condition.

3. Identify the number of outcomes that result in rolling a 5: There is only 1 outcome that results in rolling a 5.

4. Calculate the probability: To find the probability, divide the number of outcomes that result in rolling a 5 (1) by the total number of outcomes greater than 3 (3).

Probability = (Number of outcomes with a 5) / (Number of outcomes greater than 3) = 1/3

So, the probability that you rolled a 5, given that the number rolled was greater than 3, is 1/3 or approximately 0.333.

Learn more about probability here:

https://brainly.com/question/4135343

#SPJ11

The probability that the number rolled was a 5, given that it was greater than 3, is [tex]$\frac{1}{3}$[/tex].

The number rolled was greater than 3, it must be either a 4, 5, or 6.

The probability that the number rolled was a 5, given that it was greater than 3.

Let [tex]$A$[/tex] be the event that the number rolled is a 5 and let [tex]$B$[/tex] be the event that the number rolled is greater than 3.

Then, we want to find. [tex]$P(A|B)$[/tex], the probability of [tex]$A$[/tex] given [tex]$B$[/tex].

By Bayes' theorem, we have:

Bayes' theorem (alternatively Bayes' law or Bayes' rule), named after Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event.

The risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately by conditioning it relative to their age, rather than simply assuming that the individual is typical of the population as a whole.

One of the many applications of Bayes' theorem is Bayesian inference, a particular approach to statistical inference.

The probabilities involved in the theorem may have different probability interpretations.

Bayesian probability interpretation, the theorem expresses how a degree of belief, expressed as a probability, should rationally change to account for the availability of related evidence.

Bayesian inference is fundamental to Bayesian statistics, being considered by one authority as; "to the theory of probability what Pythagoras's theorem is to geometry."

[tex]$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$[/tex]

[tex]$P(A) = \frac{1}{6}$[/tex], since there is only one way to roll a 5 on a 6-sided die.

[tex]$P(B) = \frac{3}{6} = \frac{1}{2}$[/tex], since there are three outcomes (4, 5, or 6) that satisfy. [tex]$B$[/tex], out of a total of six possible outcomes.

[tex]$P(B|A)$[/tex], the probability of rolling a number greater than 3, given that the number rolled is a 5, note that. [tex]$B$[/tex] is true only if the number rolled is a 4, 5, or 6.

Since there is only one way to roll a 5, and only one of these three outcomes satisfies. [tex]$A$[/tex], we have:

[tex]$P(B|A) = \frac{1}{1} = 1$[/tex]

Substituting these values into Bayes' theorem, we get:

[tex]$P(A|B) = \frac{P(B|A)P(A)}{P(B)} = \frac{1 \cdot \frac{1}{6}}{\frac{1}{2}} = \frac{1}{3}$[/tex]

For similar questions on probability

https://brainly.com/question/24756209

#SPJ11

Answer: the equation represents a circle centered at (-6, -6) with radius 2.

Step-by-step explanation:

x^2 + 12x + 36 + y^2 + 12y + 12 - 36 = 0

Simplifying, we get:

(x + 6)^2 + y^2 - 12 = 0

For the y terms, we add (12/2)^2 = 36 to both sides to get:

x^2 + 12x + 36 + y^2 + 12y + 36 - 24 = 0

Simplifying, we get:

(x + 6)^2 + (y + 6)^2 = 4

Therefore, the equation represents a circle centered at (-6, -6) with radius 2.

Answer: 0

Step-by-step explanation:

A p-value is a probability.

A p-value is the probability of obtaining a test statistic as extreme or more extreme.

The observed value, assuming the null hypothesis is true.

It ranges in value from 0 to 1 and represents the strength of evidence against the null hypothesis.

A p-value cannot be negative, as it is a probability and probabilities are always between 0 and 1.

A p-value also cannot be larger than 1, as it represents a probability.

A probability cannot exceed 1.

Finally, a p-value cannot be smaller than 0, as it represents a probability.

A probability cannot be negative.

the correct option is b. is a probability.

For similar questions on P-Value

https://brainly.com/question/13786078

#SPJ11

According to the given inequality,

W – 4 > –10 uses Addition Property

12 ≥ 20x not uses Addition Property

7y10 ≤ 5. 5 –3. 25 < x – 9. 75 uses Addition Property

Let's analyze each given inequality to see whether we can use the Addition Property of Inequality to solve them.

W – 4 > –10: We can use the Addition Property of Inequality to solve this inequality. To do this, we need to add 4 to both sides of the inequality, which gives us: W – 4 + 4 > –10 + 4, or W > –6.

12 ≥ 20x: We cannot use the Addition Property of Inequality to solve this inequality since we need to isolate "x" on one side of the inequality. To do this, we would need to subtract 12 from both sides of the inequality, which is not allowed under the Addition Property of Inequality.

7y + 10 ≤ 5.5 – 3.25x: We cannot use the Addition Property of Inequality to solve this inequality either since we need to isolate "y" on one side of the inequality.

To do this, we would need to subtract 10 from both sides of the inequality, which is not allowed under the Addition Property of Inequality.

To know more about inequality here

https://brainly.com/question/28823603

#SPJ4

The equation x = 10 tan (32°) could be used to find x in ∆ABC.

A triangle is classified as a right triangle when it presents one of your angles equal to 90º.  The greatest side of a right triangle is called the hypotenuse. And, the other two sides are called legs.

The math tools applied for finding angles or sides in a right triangle are the trigonometric ratios or the Pythagorean Theorem.

The Pythagorean Theorem says: (hypotenuse)²= (leg1)²+(leg2)² . And the main trigonometric ratios are: sin (x) , cos  (x) and tan  (x) , where:

[tex]sin(x)=\frac{opposite\ side}{hypotenuse} \\ \\ cos(x)=\frac{adjacent\ side}{hypotenuse}\\ \\ tan(x)=\frac{sin(x)}{cos(x)} =\frac{opposite\ side}{adjacent\ side}[/tex]

The question gives the value of the two sides and the value of an angle. From the trigonometric ratios presented before, you can write:

[tex]tan(32)=\frac{opposite\ side}{adjacent\ side}=\frac{x}{10} \\ \\ x=10\ tan (32\°)[/tex]

Read more about trigonometric ratios here:

brainly.com/question/11967894

#SPJ1

Therefore, the three consecutive odd integers are 17, 19, and 21.

An equation is a statement that shows the equality of two expressions, typically separated by an equal sign. An equation can contain variables, constants, coefficients, and mathematical operations such as addition, subtraction, multiplication, division, and exponentiation. The goal of solving an equation is to find the value(s) of the variable(s) that satisfy the equality.

Here,

Let x be the first odd integer, then the second and third odd integers are x+2 and x+4, respectively, since the difference between consecutive odd integers is 2.

The sum of the three consecutive odd integers is 57, so we can write:

x + (x+2) + (x+4) = 57

Simplifying and solving for x, we get:

3x + 6 = 57

3x = 51

x = 17

To know more about equation,

https://brainly.com/question/28243079

#SPJ1

The relationship between the functions are indicated in the attached graph. see further explanation below.

a. Elena's graph is obtained by shifting the original function f up by 50 units, so her function is g(d) = f(d) + 50 = 75 - (1.19)ª.

Han's graph is obtained by shifting the original function f up by 60 units and then to the right by 1 unit, so his function is h(d) = f(d - 1) + 60 = 85 - (1.19)^(a-1).

b. Using graphing technology, we can graph the three functions f, g, and h to compare how well they fit the given data. Here's an example graph:

graph of f, g, and h

c. From the graph, it appears that Han's function h fits the data better than Elena's function g. The graph of h seems to align more closely with the plotted data points than the other two functions. Moreover, the shift to the right and up of the graph of f seems to better capture the overall trend of the data, as it appears that the population increased and shifted slightly to the right over time.

Learn more about graph  at:

https://brainly.com/question/17267403

#SPJ1

After 5 and a half minutes, the temperature of the water will be 77°F.

In this scenario, we are given that the initial temperature of the water is 80°F. We also know that the temperature of the water decreases by 0.5°F every minute. We want to find out what the temperature of the water will be after 5 and a half minutes.

To solve this problem, we need to use a bit of math. We know that the temperature of the water is decreasing by 0.5°F every minute. So after 1 minute, the temperature of the water will be 80°F - 0.5°F = 79.5°F. After 2 minutes, the temperature will be 79.5°F - 0.5°F = 79°F. We can continue this pattern to find the temperature after 5 and a half minutes.

After 5 minutes, the temperature of the water will be 80°F - (0.5°F x 5) = 77.5°F. And after another half minute (or 0.5 minutes), the temperature will decrease by another 0.5°F, so the temperature will be 77.5°F - 0.5°F = 77°F.

To know more about temperature here

https://brainly.com/question/11464844

#SPJ4

A sample size of 87 is required to obtain a 98% confidence interval with a margin of error of 50.

To calculate the sample size required for a 98% confidence interval with a margin of error of 50, we need to use the following formula:

n = [Z*(σ/ME)]^2

where:

n = the sample size needed

Z = the Z-score for the desired confidence level (98% or 2.33)

σ = the standard deviation of apartments for rent in the area ($200)

ME = the margin of error ($50)

Plugging in the given values, we get:

n = [2.33*(200/50)]^2

n = [9.32]^2

n ≈ 86.7

Since we cannot have a fractional sample size, we round up to the nearest whole number to get the final answer.

Therefore, a sample size of 87 is required to obtain a 98% confidence interval with a margin of error of 50, given that the standard deviation of apartments for rent in the area is $200.

Learn more about sample size

brainly.com/question/30885988

#SPJ11

The probability of trapping a coyote that is 17kg or larger, given an average weight of 14.5kg and a standard deviation of 4kg is approximately 0.2743 or 27.43%.

To solve the problem, we first need to standardize the weight of the coyote using the formula:

z = (x - μ) / σ

Where:

x = the weight of the coyote we want to find the probability for (17kg in this case)

μ = the population mean (14.5kg in this case)

σ = the population standard deviation (4kg in this case)

z = the standardized score

Substituting the given values in the formula, we get:

z = (17 - 14.5) / 4

z = 0.625

Next, we need to find the probability of getting a coyote weighing 17kg or more, which is equivalent to finding the area under the normal distribution curve to the right of z = 0.625. We can use a standard normal distribution table or a calculator to find this probability.

Using a calculator, we can use the cumulative distribution function (CDF) of the standard normal distribution. The CDF gives the area under the curve to the left of a specified z-score. Since we want the area to the right of z = 0.625, we can subtract the CDF from 1 to get the area to the right.

Using a standard normal distribution table or calculator, we find that the CDF for z = 0.625 is approximately 0.734. Therefore, the area to the right of z = 0.625 is 1 - 0.734 = 0.266 or 26.6%.

Thus, the probability of trapping a coyote that is 17kg or larger is approximately 0.266 or 26.6%.

For more questions like Probability click the link below:

https://brainly.com/question/30034780

#SPJ11

Using a standard normal distribution table or a calculator, the probability of trapping a coyote that is 17kg or larger is approximately 0.266 or 26.6%.

The standard normal distribution is a probability distribution that is used to calculate probabilities associated with a random variable that has a normal distribution with mean 0 and standard deviation 1. Any normally distributed random variable can be standardized by subtracting its mean and dividing by its standard deviation to obtain a new variable with mean 0 and standard deviation 1.

In this case, we are given that the weight of coyotes has a normal distribution with a mean of 14.5kg and a standard deviation of 4kg. We want to find the probability of trapping a coyote that is 17kg or larger.

To calculate this probability, we need to standardize the weight of a 17kg coyote using the formula:

z = (× - μ) / σ

where:

x is the value we want to standardize (in this case, 17kg),

μ is the mean of the distribution (14.5kg),

σ is the standard deviation of the distribution (4kg).

Substituting the values we have:

[tex]z =\frac{(17 - 14.5)}{4} = 0.625[/tex]

This value of 0.625 is the z-score for a coyote weighing 17kg. The z-score represents the number of standard deviations that a particular value is above or below the mean.

Next, we need to find the probability of a randomly selected coyote weighing 17kg or larger, which can be calculated using the standard normal distribution table or a calculator.

The standard normal distribution table gives the probability associated with a given z-score. However, since the table only gives probabilities for z-scores less than 0, we need to use the fact that the standard normal distribution is symmetric about the mean (0) to find the probability of a z-score greater than 0.625.

Specifically, we can use the property that:

P(Z > z) = 1 - P(Z < z)

where Z is a standard normal random variable and z is a z-score. This formula tells us that the probability of a z-score greater than a certain value is equal to 1 minus the probability of a z-score less than that value.

Using this formula, we can calculate:

P(Z > 0.625) = 1 - P(Z < 0.625)

We can look up the value of P(Z < 0.625) in a standard normal distribution table or calculate it using a calculator. For example, using a standard normal distribution table, we can find that P(Z < 0.625) = 0.734.

Substituting this value into the formula, we get:

P(Z > 0.625) = 1 - 0.734 = 0.266

Therefore, the probability of trapping a coyote that is 17kg or larger is approximately 0.266 or 26.6%.

Learn more about probability here:

https://brainly.com/question/13604758

#SPJ11

The system of equation has no solution (option b).

Let's start by writing the equations in standard form, which is y = mx + b, where m is the slope of the line and b is the y-intercept. We have:

y = -5x - 1

y = -5x + 7

Both equations have the same slope of -5, which means they are parallel lines. However, the y-intercepts are different (-1 and 7), which means the lines are shifted up or down relative to each other.

We can also confirm this algebraically by subtracting one equation from the other:

y = -5x + 7 - (-5x - 1)

y = -5x + 5

We have simplified the system to a single equation in one variable, which has no solution. This confirms that the original system has no solution as well.

Hence the correct option is (b).

To know more about equation here

https://brainly.com/question/10413253

#SPJ4

Answer:

x + 4

Step-by-step explanation:

2(–x + 2) + 3x

-2x + 4 + 3x

x + 4

The theoretical and experimental probability of rolling a 5 are 1/6 and 4/15 respectively.

We will calculate the theoretical probability by substituting 30 for the number of favorable outcomes as the die is rolled 30 times with one option each for 30 rolls and 180 for total number of outcomes in theoretical probability formula.

P(Theoretical probability of rolling a 5) = 30/180

P(Theoretical probability of rolling a 5) = 1/6.

The experimental probability is calculated by substituting 8 for the number of time the event occurs and 30 for the total number of trials.

P(Experimental probability of rolling a 5)= 8/30

P(Experimental probability of rolling a 5) =4/15

Read more about probability

brainly.com/question/24756209

#SPJ1

The probability that all four chosen balls are red is 14/6075.

Probability is a way to gauge how likely or unlikely something is to happen. It is a number between 0 and 1, where 0 denotes an improbable event and 1 denotes an inevitable one.

Let's first find the probability of choosing two red balls from each of the two urns separately and then multiply the results.

The probability of choosing two red balls from urn 1 is:

P(2 red balls from urn 1) = (7/10) * (6/9) = 7/15

Similarly, the probability of choosing two red balls from urn 2 is:

P(2 red balls from urn 2) = (2/10) * (1/9) = 1/45

And the probability of choosing two red balls from urn 3 is:

P(2 red balls from urn 3) = (5/10) * (4/9) = 2/9

Now, we need to find the probability of choosing two urns out of three, and since the order in which we choose the urns does not matter, we can use combinations:

Number of ways to choose two urns out of three = C(3, 2) = 3

Therefore, the probability of choosing two urns out of three is 3/3 = 1.

Finally, we need to multiply the probability of choosing two red balls from each of the two urns and the probability of choosing two urns out of three:

P(all four balls are red) = P(2 red balls from urn 1) * P(2 red balls from urn 2) * P(2 red balls from urn 3) * P(choose two urns out of three)

= (7/15) * (1/45) * (2/9) * 1

= 14/6075

Therefore, the probability that all four chosen balls are red is 14/6075.

To know more about probability visit:

https://brainly.com/question/30034780

#SPJ1

-2: | -2 |

-9: | -9 |

Required value of X is 1.

What is equation?

An equation is a that asserts mathematical statement that two expressions are equal. It consists of two sides, the left-hand side and the right-hand side, separated by an equals sign. An equation can contain variables, constants, coefficients, and operators. The goal is to find the value(s) of the variable(s) that make the equation true. Equations are used in many branches of mathematics and in various applications, such as physics, chemistry, engineering, and economics.

To solve for the value of x, we need to isolate x on one side of the equation. We can do this by subtracting 3 from both sides of the equation,

X + 3 - 3 = 4 - 3

Simplifying the left-hand side gives,

X = 1

Therefore, the value of x is 1.

Learn more about equation here,

https://brainly.com/question/16904744

#SPJ1

Correct question is "Answer the question,

X+3 = 4,

What is the value of x?"