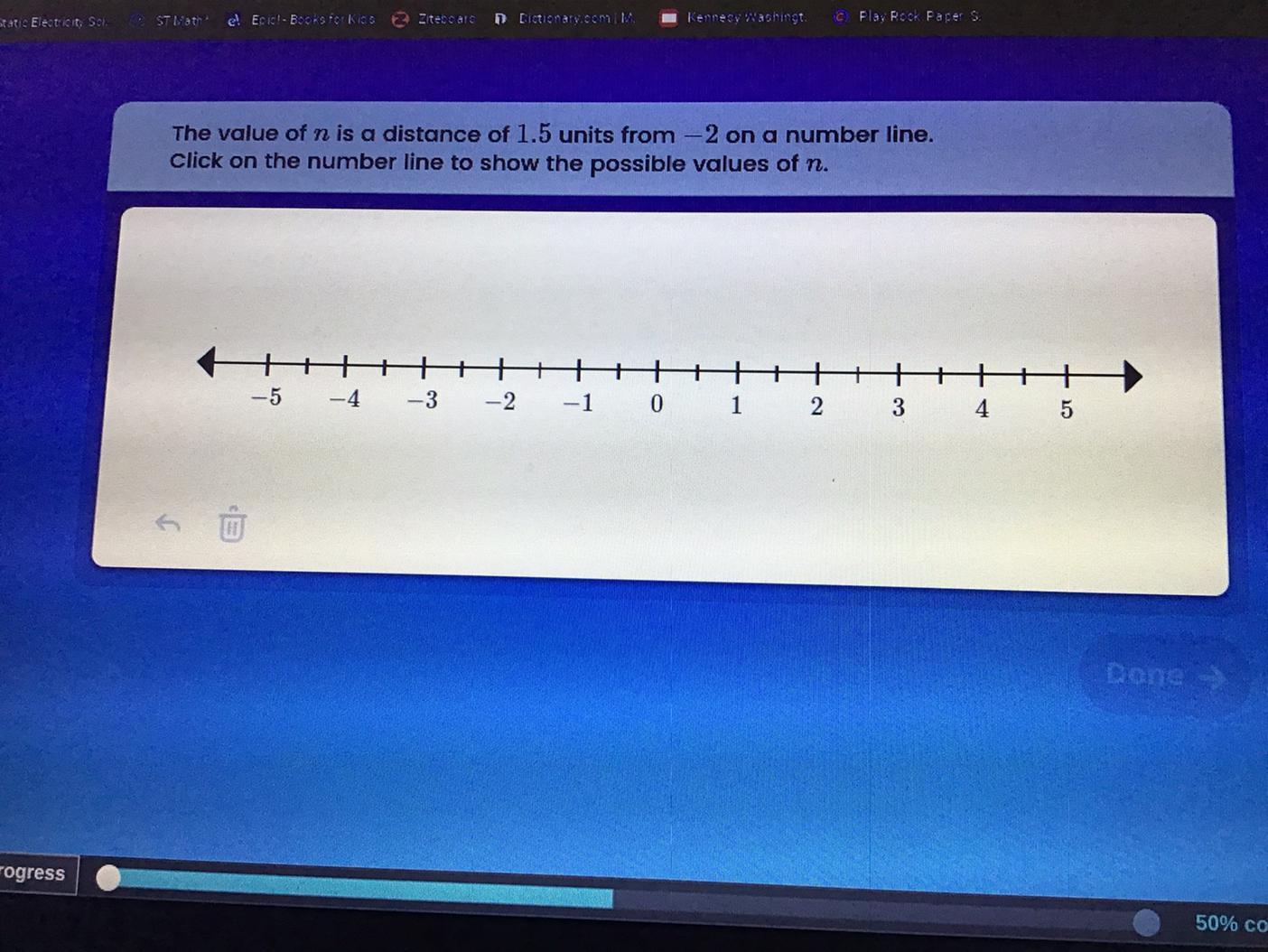
The value of n is a distance of 1.5 units from -2 on a number line.Click on the number line to show the possible values of n
Answers
Answer:
-3.5 and -0.5
Step-by-step explanation:
Related Questions
Amy is driving a racecar. The table below gives the distance Din metersshe has driven at a few times f in secondsafter she starts Distance D) (seconds) (meters) 0 3 78.3 4 147.6 6 185.4 9 287.1 (a)Find the average rate of change for the distance driven from 0 seconds to 4 seconds. meters per second b)Find the average rate of change for the distance driven from 6 seconds to 9 seconds. meters per second 5
Answers
The average rate of change for the distance driven from 6 seconds to 9 seconds is 33.9 meters per second.
To find the average rate of change for the distance driven, we need to calculate the change in distance divided by the change in time. (a) From 0 seconds to 4 seconds: The distance driven at 0 seconds is 0 meters. The distance driven at 4 seconds is 147.6 meters. The change in distance is 147.6 - 0 = 147.6 meters. The change in time is 4 - 0 = 4 seconds.
The average rate of change for the distance driven from 0 seconds to 4 seconds is: Average rate of change = Change in distance / Change in time. Average rate of change = 147.6 meters / 4 seconds = 36.9 meters per second. Therefore, the average rate of change for the distance driven from 0 seconds to 4 seconds is 36.9 meters per second.
(b) From 6 seconds to 9 seconds: The distance driven at 6 seconds is 185.4 meters. The distance driven at 9 seconds is 287.1 meters. The change in distance is 287.1 - 185.4 = 101.7 meters. The change in time is 9 - 6 = 3 seconds. The average rate of change for the distance driven from 6 seconds to 9 seconds is: Average rate of change = Change in distance / Change in time. Average rate of change = 101.7 meters / 3 seconds = 33.9 meters per second. Therefore, the average rate of change for the distance driven from 6 seconds to 9 seconds is 33.9 meters per second.
To learn more about rate, click here: brainly.com/question/29204803
#SPJ11
You build a linear regression model that predicts the price of a house using two features: number of bedrooms (a), and size of the house (b). The final formula is: price = 100 + 10 * a - 1 * b. Which statement is correct:
(15 Points)
Increasing the number of bedrooms (a) will increase the price of a house
increasing size of the house (b) will decrease the price of a house
both above
When it comes to such interpretations, the safest answer is: I don't know
Answers
The linear regression model means (c) both statements are true
Increasing the number of bedrooms (a) will increase the price of a house. Increasing the size of the house (b) will decrease the price of a house.How to interpret the linear regression modelFrom the question, we have the following parameters that can be used in our computation:
y = 100 + 10 * a - 1 * b
From the above, we can see the coefficients of a and b to be
a = positive
b = negative
This means that
Certain factors will increase the price of house aCertain factors will decrease the price of house bThis in other words means that
The options a and b are true, and such the true statement is (c) both above
Read more about linear regression at
https://brainly.com/question/26755306
#SPJ4
In a gambling game, a player wins the game if they roll 10 fair, six-sided dice, and get a sum of at least 40.
Approximate the probability of winning by simulating the game 104 times.
1. Complete the following R code. Do not use any space.
set.seed (200)
rolls
=
replace=
)
result =
rollsums
)
sample(x=1:6, size=
matrix(rolls, nrow-10^4, ncol=10)
apply(result, 1,
2. In the setting of Question 1, what is the expected value of the random variable Y="sum of 10 dice"? Write an integer.
3. In the setting of Question 1, what is the variance of the random variable Y= "sum of 10 dice"? Use a number with three decimal places.
4. Using the code from Question 1, what is the probability of winning? Write a number with three decimal places.
5. In the setting of Question 1, using the Central Limit Theorem, approximate P (Y>=40). What is the absolute error between this value and the Monte Carlo error computed before? Write a number with three decimal places.
Answers
1. Here is the completed R code:
```R
set.seed(200)
rolls <- sample(x = 1:6, size = 10^4 * 10, replace = TRUE)
result <- matrix(rolls, nrow = 10^4, ncol = 10)
win_prob <- mean(apply(result, 1, function(x) sum(x) >= 40))
win_prob
```
2. The expected value of the random variable Y, which represents the sum of 10 dice, can be calculated as the sum of the expected values of each die. Since each die has an equal probability of landing on any face from 1 to 6, the expected value of a single die is (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5. Therefore, the expected value of the sum of 10 dice is 10 * 3.5 = 35.
3. The variance of the random variable Y, which represents the sum of 10 dice, can be calculated as the sum of the variances of each die. Since each die has a variance of [(1 - 3.5)^2 + (2 - 3.5)^2 + (3 - 3.5)^2 + (4 - 3.5)^2 + (5 - 3.5)^2 + (6 - 3.5)^2] / 6 = 35 / 12 ≈ 2.917.
4. Using the code from Question 1, the probability of winning is the estimated win_prob. The result from the code will provide this probability, which should be rounded to three decimal places.
5. To approximate P(Y >= 40) using the Central Limit Theorem (CLT), we need to calculate the mean and standard deviation of the sum of 10 dice. The mean of the sum of 10 dice is 35 (as calculated in Question 2), and the standard deviation is √(10 * (35 / 12)) ≈ 9.128. We can then use the CLT to approximate P(Y >= 40) by finding the probability of a standard normal distribution with a z-score of (40 - 35) / 9.128 ≈ 0.547. This value can be looked up in a standard normal distribution table or calculated using software. The absolute error between this approximation and the Monte Carlo error can be obtained by subtracting the Monte Carlo win probability from the CLT approximation and taking the absolute value.
Learn more about Central Limit Theorem here: brainly.com/question/23995384
#SPJ11
In this problem we'd like to solve the boundary value problem Ə x = 4 Ə 2u
Ə t Ə x2
on the interval [0, 4] with the boundary conditions u(0, t) = u(4, t) = 0 for all t.
(a) Suppose h(x) is the function on the interval [0, 4] whose graph is is the piecewise linear function connecting the points (0, 0), (2, 2), and (4,0). Find the Fourier sine series of h(z): h(x) = - Σ bx (t) sin (nkx/4).
Please choose the correct option: does your answer only include odd values of k, even values k, or all values of k? bk(t) (16/(k^2pi^2)){(-1)^{(k-1)/2))
Which values of k should be included in this summation? A. Only the even values B. Only the odd values C. All values (b) Write down the solution to the boundary value problem Ə x = 4 Ə 2u
Ə t Ə x2
on the interval [0, 4] with the boundary conditions u(0, t) = u(4, t) = 0 for all t subject to the initial conditions u(a,0) = h(a). As before, please choose the correct option: does your answer only include odd values of k, even values of k, or all values of ? [infinity]
u(x, t) = Σ
k-1 Which values of k should be included in this summation? A. Only the even values B. Only the odd values C. All values 4 br(t) sin
Previous question
Answers
a) Since all the coefficients bx(t) are equal to 0, the Fourier sine series of h(x) does not contain any terms. Hence, the answer is option C: All values of k.
(a) To find the Fourier sine series of the function h(x), we need to determine the coefficients bx(t). The function h(x) is a piecewise linear function that connects the points (0, 0), (2, 2), and (4, 0).
The Fourier sine series representation of h(x) is given by:
h(x) = - Σ bx(t) sin(nkx/4)
To find the coefficients bx(t), we can use the formula:
bx(t) = (2/L) ∫[0,L] h(x) sin(nkx/4) dx
In this case, L = 4 (interval length).
Calculating bx(t) for the given values of h(x), we have:
b₀(t) = (2/4) ∫[0,4] h(x) sin(0) dx = 0
or n > 0:
bn(t) = (2/4) ∫[0,4] h(x) sin(nkx/4) dx
Let's consider the three intervals separately:
For 0 ≤ x ≤ 2:
bn(t) = (2/4) ∫[0,2] 2 sin(nkx/4) dx = (1/2) ∫[0,2] sin(nkx/4) dx
Using the trigonometric identity ∫ sin(ax) dx = -1/a cos(ax) + C, we have:
bn(t) = (1/2) [-4/(nkπ) cos(nkx/4)] [0,2]
bn(t) = (-2π/nk) [cos(nk) - cos(0)]
bn(t) = (-2π/nk) (1 - cos(0))
bn(t) = (-2π/nk) (1 - 1)
bn(t) = 0
For 2 ≤ x ≤ 4:
bn(t) = (2/4) ∫[2,4] 0 sin(nkx/4) dx = 0
Therefore, the Fourier sine series of h(x) is:
h(x) = - Σ bx(t) sin(nkx/4)
= 0
(b) The solution to the boundary value problem with the given boundary conditions and initial conditions is not provided in the given information. Please provide the specific initial condition, and I can help you with the solution.
To know more about trigonometric visit;
brainly.com/question/29156330
#SPJ11
4. (2 points) Suppose A € Mnn (R) and A³ = A. Show that the the only possible eigenvalues of A are λ = 0, λ = 1, and λ = -1.
Answers
Values of λ are eigenvalues is 0, 1 or -1.
Given a matrix A ∈ M_n×n(R) such that A³ = A.
We are to prove that only possible eigenvalues of A are λ = 0, λ = 1, and λ = -1.
If λ is an eigenvalue of A, then there is a nonzero vector x ∈ R^n such that Ax = λx.
So, A³x = A(A²x) = A(A(Ax)) = A(A(λx)) = A(λAx) = λ²(Ax) = λ³x.
Hence, we can say that A³x = λ³x.
Since A³ = A, it follows that λ³x = Ax = λx which implies (λ³ - λ)x = 0.
Since x ≠ 0, it follows that λ³ - λ = 0 i.e. λ(λ² - 1) = 0.
Hence, λ is 0, 1 or -1.
Learn more about eigenvalues
brainly.com/question/29861415
#SPJ11
Let (G₁,+) and (G2, +) be two subgroups of (R, +) so that Z+G₁ G₂. If o: G₁ G₂ is a group isomorphism with o(1) = 1, show that o(n): = n for all n € Z+. Hint: consider using mathematical induction.
Answers
To prove that o(n) = n for all n ∈ Z+, we can use mathematical induction.
Step 1: Base Case
Let's start with the base case when n = 1.
Since o is a group isomorphism with o(1) = 1, we have o(1) = 1.
Therefore, the base case holds.
Step 2: Inductive Hypothesis
Assume that o(k) = k for some arbitrary positive integer k, where k ≥ 1.
Step 3: Inductive Step
We need to show that o(k + 1) = k + 1 using the assumption from the inductive hypothesis.
Using the properties of a group isomorphism, we have:
o(k + 1) = o(k) + o(1).
From the inductive hypothesis, o(k) = k, and since o(1) = 1, we can substitute these values into the equation:
o(k + 1) = k + 1.
Therefore, the statement holds for k + 1.
By the principle of mathematical induction, we can conclude that o(n) = n for all n ∈ Z+.
learn more about isomorphism here: brainly.com/question/31963964
#SPJ11
of Let f(x,y)=tanh=¹(x−y) with x=e" and y= usinh (1). Then the value of (u,1)=(4,In 2) is equal to (Correct to THREE decimal places) evaluated at the point
Answers
The value of f(x,y) = tanh^(-1)(x-y) at the point (x=e^(-1), y=usinh(1)) with (u,1)=(4,ln(2)) is approximately 0.649. The expressions are based on hyperbolic tangent function.To evaluate the expression f(x,y) = tanh^(-1)(x-y), we substitute the given values of x and y.
x = e^(-1)
y = usinh(1) = 4sinh(1) = 4 * (e - e^(-1))/2
Substituting these values into the expression, we have:
f(x,y) = tanh^(-1)(e^(-1) - 4 * (e - e^(-1))/2)
Simplifying further:
f(x,y) = tanh^(-1)(e^(-1) - 2(e - e^(-1)))
Now we substitute the value of e = 2.71828 and evaluate the expression:
f(x,y) = tanh^(-1)(2.71828^(-1) - 2(2.71828 - 2.71828^(-1)))
= tanh^(-1)(0.36788 - 2(0.71828 - 0.36788))
= tanh^(-1)(0.36788 - 2(0.3504))
= tanh^(-1)(0.36788 - 0.7008)
= tanh^(-1)(-0.33292)
≈ 0.649
Therefore, the value of f(x,y) = tanh^(-1)(x-y) at the point (u,1)=(4,ln(2)) is approximately 0.649.
To know more about the hyperbolic tangent function refer here:
https://brainly.com/question/22161213#
#SPJ11
(a) What is meant by the determinant of a matrix? What is the significance to the matrix if its determinant is zero?
(b) For a matrix A write down an equation for the inverse matrix in terms of its determinant, det A. Explain in detail the meaning of any other terms employed.
(c) Calculate the inverse of the matrix for the system of equations below. Show all steps including calculation of the determinant and present complete matrices of minors and co-factors. Use the inverse matrix to solve for x, y and z.
2x + 4y + 2z = 8
6x-8y-4z = 4
10x + 6y + 10z = -2
Answers
(a) The determinant of a matrix is a scalar value that is calculated from the elements of the matrix. It is defined only for square matrices, meaning the number of rows is equal to the number of columns. The determinant provides important information about the matrix, such as whether it is invertible and the properties of its solutions.
If the determinant of a matrix is zero, it means that the matrix is singular or non-invertible. This implies that the matrix does not have an inverse. In practical terms, a determinant of zero indicates that the system of equations represented by the matrix either has no solution or infinitely many solutions. It also signifies that the matrix's rows or columns are linearly dependent, leading to a loss of information and a lack of unique solutions.
(b) For a square matrix A, the equation for its inverse matrix can be expressed as A^(-1) = (1/det A) * adj A, where det A represents the determinant of matrix A, and adj A represents the adjugate of matrix A. The adjugate of matrix A is obtained by transposing the matrix of cofactors, where each element in the matrix of cofactors is the signed determinant of the minor matrix obtained by removing the corresponding row and column from matrix A.
In this equation, the determinant (det A) is used to scale the adjugate matrix to obtain the inverse matrix. The determinant is also crucial because it determines whether the matrix is invertible or singular, as mentioned earlier.
(c) To calculate the inverse of the matrix for the given system of equations, we need to follow these steps:
1. Set up the coefficient matrix A using the coefficients of the variables x, y, and z.
A = | 2 4 2 |
| 6 -8 -4 |
|10 6 10 |
2. Calculate the determinant of matrix A: det A.
det A = 2(-8*10 - (-4)*6) - 4(6*10 - (-4)*10) + 2(6*6 - (-8)*10)
= 2(-80 + 24) - 4(-60 + 40) + 2(36 + 80)
= 2(-56) - 4(-20) + 2(116)
= -112 + 80 + 232
= 200
3. Find the matrix of minors by calculating the determinants of the minor matrices obtained by removing each element of matrix A.
Minors of A:
| -32 -12 24 |
| -44 -16 16 |
| 84 12 24 |
4. Create the matrix of cofactors by multiplying each element of the matrix of minors by its corresponding sign.
Cofactors of A:
| -32 12 24 |
| 44 -16 -16 |
| 84 12 24 |
5. Transpose the matrix of cofactors to obtain the adjugate matrix.
Adj A:
| -32 44 84 |
| 12 -16 12 |
| 24 -16 24 |
6. Finally, calculate the inverse matrix using the formula A^(-1) = (1/det A) * adj A.
A^(-1) = (1/200) * | -32 44 84 |
| 12 -16 12 |
| 24 -16 24 |
To solve for x, y, and z, we can multiply the inverse matrix by the
To learn more about Matrix - brainly.com/question/28180105
#SPJ11
Write the given system of differential equations using matrices and solve. Show work to receive full credit.
x'=x+2y-z
y’ = x + z
z’ = 4x - 4y + 5z
Answers
The general solution of the given system of differential equations is: x = c1 ( e^(-t) )+ c2 ( e^(4t) )+ 4t - 2y = c1 ( e^(-t) )- c2 ( e^(4t) )- 2t + 1z = -c1 ( e^(-t) )+ c2 ( e^(4t) )+ t
Given system of differential equations using matrices :y’ = x + zz’ = 4x - 4y + 5z. To solve the above given system of differential equations using matrices, we need to write the above system of differential equations in matrix form. Matrix form of the given system of differential equations :y' = [ 1 0 1 ] [ x y z ]'z' = [ 4 -4 5 ] [ x y z ]'Using the above matrix equation, we can find the solution as follows:∣ [ 1-λ 0 1 0 ] [ 4 4-λ 5 ] ∣= (1-λ)(-4+λ)-4*4= λ² -3 λ - 16 =0Solving this quadratic equation for λ, we get, λ= -1, 4. Using these eigenvalues, we can find the corresponding eigenvectors for each of the eigenvalues λ = -1, 4.
Know more about differential equations here:
https://brainly.com/question/31492438
#SPJ11
You arrive in a condo building and are about to take the elevator to the 3rd floor where you live. When you press the button, it takes anywhere between 0 and 40 seconds for the elevator to arrive to you. Assume that the elevator arrives uniformly between 0 and 40 seconds after you press the button. The probability that the elevator will arrive sometime between 15 and 27 seconds is State your answer as a percent and include the % sign. Fill in the blank 0.68
Answers
The probability that the elevator will arrive sometime between 15 and 27 seconds after pressing the button can be calculated by finding the proportion of the total time range (0 to 40 seconds) that falls within the given interval. Based on the assumption of a uniform distribution, the probability is determined by dividing the length of the desired interval by the length of the total time range. The result is then multiplied by 100 to express the probability as a percentage.
The total time range for the elevator to arrive is given as 0 to 40 seconds. To calculate the probability that the elevator will arrive sometime between 15 and 27 seconds, we need to find the proportion of this interval within the total time range.
The length of the desired interval is 27 - 15 = 12 seconds. The length of the total time range is 40 - 0 = 40 seconds.
To find the probability, we divide the length of the desired interval by the length of the total time range:
Probability = (length of desired interval) / (length of total time range) = 12 / 40 = 0.3
Finally, to express the probability as a percentage, we multiply by 100:
Probability as a percentage = 0.3 * 100 = 30%
Therefore, the probability that the elevator will arrive sometime between 15 and 27 seconds is 30%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
3. The decimal expansion of 13/625 will terminate
after how many places of decimal?
(a) 1
(b) 2
(c) 3
(d) 4
Answers
The decimal expansion of the given fraction is 0.0208. Therefore, the correct answer is option D.
The given fraction is 13/625.
Decimals are one of the types of numbers, which has a whole number and the fractional part separated by a decimal point.
Here, the decimal expansion is 13/625 = 0.0208
So, the number of places of decimal are 4.
Therefore, the correct answer is option D.
To learn more about the decimal numbers visit:
https://brainly.com/question/1578006.
#SPJ1
find f · dr c for the given f and c. f = x2 i y2 j and c is the top half of a circle of radius 2 starting at the point (2, 0) traversed counterclockwise.
Answers
Let f be a continuous vector field defined on a smooth curve C that has a parametrization r(t), a ≤ t ≤ b, given by r(t) = (x(t), y(t)). Then, the line integral of f along C is given by ∫CF·dr = ∫ba F(x(t), y(t)) · r'(t) dt.where F = f · T and T is the unit tangent vector to C, that is T = r'(t) / ||r'(t)||.
To apply this formula, we need to find a parametrization r(t) for the top half of a circle of radius 2 starting at the point (2, 0) traversed counterclockwise. One way to do this is to use the polar coordinates r = 2 and θ ranging from π to 2π, which correspond to the x-coordinates ranging from 0 to −2 along the top half of the circle. Thus, we can setx(t) = 2 − 2 cos t, y(t) = 2 sin t, π ≤ t ≤ 2πThen, we have r'(t) = (2 sin t, 2 cos t) and ||r'(t)|| = 2, so T(t) = r'(t) / ||r'(t)|| = (sin t, cos t).Next, we need to compute F(x, y) = f · T for the given f = x^2 i + y^2 j. We have T(t) = (sin t, cos t), so F(x(t), y(t)) = (x(t))^2 sin t + (y(t))^2 cos t= (2 − 2 cos t)^2 sin t + (2 sin t)^2 cos t= 4 (1 − cos t)^2 sin t + 4 sin^3 t= 4 (sin^3 t − 3 sin^2 t cos t + 3 sin t cos^2 t − cos^3 t) + 4 sin^3 t= 8 sin^3 t − 12 sin^2 t cos t + 12 sin t cos^2 t − 4 cos^3 tThus, the line integral of f along C is∫CF·dr = ∫2ππ F(x(t), y(t)) · r'(t) dt= ∫2ππ [8 sin^3 t − 12 sin^2 t cos t + 12 sin t cos^2 t − 4 cos^3 t] [2 sin t, 2 cos t] dt= 4 ∫2ππ [4 sin^4 t − 6 sin^2 t cos^2 t + 6 sin^2 t cos^2 t − 2 cos^2 t] [sin t, cos t] dt= 4 ∫2ππ [4 sin^4 t − 2 cos^2 t] sin t dt= 4 ∫2ππ [2 sin^2 t − cos^2 t] [2 sin t cos t] dt= 16 ∫2ππ sin^3 t cos t dtTo evaluate this integral, we can use the substitution u = sin t, du = cos t dt and get∫2ππ sin^3 t cos t dt = ∫01 u^3 du = 1/4Thus, the line integral of f along C is ∫CF·dr = 16(1/4) = 4Therefore, the answer is 4.
The line integral of f along the top half of a circle of radius 2 starting at the point (2, 0) traversed counterclockwise, where f = x^2 i + y^2 j, is 4.
To learn more about vector visit:
brainly.com/question/31265178
#SPJ11
At least one of the answers above is NOT correct. (1 point) The composition of the earth's atmosphere may have changed over time. To try to discover the nature of the atmosphere long ago, we can examine the gas in bubbles inside ancient amber. Amber is tree resin that has hardened and been trapped in rocks. The gas in bubbles within amber should be a sample of the atmosphere at the time the amber was formed. Measurements on specimens of amber from the late Cretaceous era (75 to 95 million years ago) give these percents of nitrogen: 63.4 65.0 64.4 63.3 54.8 64.5 60.8 49.1 51.0 Assume (this is not yet agreed on by experts) that these observations are an SRS from the late Cretaceous atmosphere. Use a 99% confidence interval to estimate the mean percent of nitrogen in ancient air. % to %
Answers
The 99% confidence interval for the mean percent of nitrogen in ancient air is (50.49, 71.47)$ Therefore, option D is the correct answer.
The formula for a confidence interval is given by:
[tex]\large\overline{x} \pm z_{\alpha / 2} \cdot \frac{s}{\sqrt{n}}[/tex]
Here,
[tex]\overline{x} = \frac{63.4+65.0+64.4+63.3+54.8+64.5+60.8+49.1+51.0}{9} \\= 60.98[/tex]
[tex]s = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i - \overline{x})^2} = 6.6161[/tex]
We have a sample of size n = 9.
Using the t-distribution table with 8 degrees of freedom, we get:
[tex]t_{\alpha/2, n-1} = t_{0.005, 8} \\= 3.355[/tex]
Now, substituting the values in the formula we get,
[tex]\large 60.98 \pm 3.355 \cdot \frac{6.6161}{\sqrt{9}}[/tex]
The 99% confidence interval for the mean percent of nitrogen in ancient air is (50.49, 71.47). Therefore, option D is the correct answer.
Know more about 99% confidence interval here:
https://brainly.com/question/17097944
#SPJ11
1. Given |äl=6, |b|=5 and the angle between the 2 vectors is 95° calculate a . b
Answers
The dot product is approximately -2.6136.
What is the dot product approximately?To calculate the dot product of vectors a and b, we can use the formula:
a . b = |a| |b| cos(θ)
Given that |a| = 6, |b| = 5, and the angle between the two vectors is 95°, we can substitute these values into the formula:
a . b = 6 * 5 * cos(95°)
Using a calculator, we can find the cosine of 95°, which is approximately -0.08716. Plugging this value into the equation:
a . b = 6 * 5 * (-0.08716) = -2.6136
Therefore, the dot product of vectors a and b is approximately -2.6136.
Learn more about dot product
brainly.com/question/23477017
#SPJ11
.Find the vertices and the foci of the ellipse with the given equation. Then draw its graph.
5x² +2y² =10
Answers
To find the vertices and the foci of the ellipse with the given equation 5x² +2y² =10, we will use the standard form of the equation of an ellipse, x²/a²+y²/b²=1.
In this equation, a represents the horizontal distance from the center to the vertex or the foci and b represents the vertical distance from the center to the vertex or the foci.
For this problem, we can see that the major axis is along the x-axis since the coefficient of x² is larger than the coefficient of y². Therefore, a²=10/5=2 and b²=10/2=5.
This means that a=√2 and b=√5. The center of the ellipse is (0,0). Therefore, the vertices of the ellipse are (±√2,0), and the foci of the ellipse are (±√3,0).To draw the graph, we can first plot the center of the ellipse at (0,0). Then, we can draw the major axis, which is a horizontal line passing through the center and has a length of 2√2. This line passes through the vertices (±√2,0).
Then, we can draw the minor axis, which is a vertical line passing through the center and has a length of 2√5. This line passes through the points (0,±√5). Finally, we can draw the ellipse by sketching a curve that smoothly connects the vertices and the ends of the minor axis.To find the vertices and the foci of an ellipse from its given equation, we first need to check its standard form.
An ellipse is the set of all points in a plane such that the sum of their distances from two fixed points (called foci) is constant. Therefore, the equation of an ellipse must have the form x²/a²+y²/b²=1 or y²/a²+x²/b²=1, where a represents the horizontal distance from the center to the vertex or the foci and b represents the vertical distance from the center to the vertex or the foci.
In this case, the given equation is 5x²+2y²=10, which can be rewritten as x²/2+y²/5=1 by dividing both sides by 10. Therefore, we can see that a²=2 and b²=5. This means that a=√2 and b=√5.
The center of the ellipse is (0,0). Therefore, the vertices of the ellipse are (±√2,0), and the foci of the ellipse are (±√3,0).To draw the graph of the ellipse, we can first plot the center of the ellipse at (0,0).
Then, we can draw the major axis, which is a horizontal line passing through the center and has a length of 2√2. This line passes through the vertices (±√2,0). Then, we can draw the minor axis, which is a vertical line passing through the center and has a length of 2√5. This line passes through the points (0,±√5). Finally, we can draw the ellipse by sketching a curve that smoothly connects the vertices and the ends of the minor axis. This curve should have a shape that is somewhat similar to a stretched-out circle.
Therefore, the vertices of the given ellipse are (±√2,0), and the foci of the given ellipse are (±√3,0). The graph of the ellipse can be drawn by plotting the center at (0,0), drawing the major and minor axes passing through the center and having lengths of 2√2 and 2√5, respectively, and then sketching a curve that connects the vertices and the ends of the minor axis.
To know more about foci visit:
brainly.com/question/31881782
#SPJ11
Write a system of equations that is equivalent to the vector equation:
3 -5 -16
x1= 16 = x2=0 = -10
-8 10 5
a. 3x1 - 5x2 = 5
16x1 = -15
-8x1 + 13x2 = -16
b. 3x1 - 5x2 = -16
16x1 = -15
-8x1 + 13x2 = 5
c. 3x1 - 5x2 = -16
16x1 + 5x2 = -10
-8x1 + 13x2 = -5
d. 3x1 - 5x2 = -10
16x1 = -16
-8x1 + 13x2 = 5
Answers
The correct system of equations that is equivalent to the vector equation is: c. 3x₁ - 5x₂ = -16
16x₁ + 5x₂ = -10
-8x₁ + 13x₂ = -5
We can convert the vector equation into a system of equations by equating the corresponding components of the vectors.
The vector equation is:
(3, -5, -16) = (16, 0, -10) + x₁(0, 1, 0) + x₂(-8, 10, 5)
Expanding the equation component-wise, we have:
3 = 16 + 0x₁ - 8x₂
-5 = 0 + x₁ + 10x₂
-16 = -10 + 0x₁ + 5x₂
Simplifying these equations, we get:
3 - 16 = 16 - 8x₂
-5 = x₁ + 10x₂
-16 + 10 = -10 + 5x₂
Simplifying further:
-13 = -8x₂
-5 = x₁ + 10x₂
-6 = 5x₂
Dividing the second equation by 10:
-1/2 = x₁ + x₂
So, the system of equations that is equivalent to the vector equation is:
3x₁ - 5x₂ = -16
16x₁ + 5x₂ = -10
-8x₁ + 13x₂ = -5
To know more about vector visit:
brainly.com/question/24256726
#SPJ11
Find the determinant of
1 7 -1 0 -1
2 4 7 0 0
3 0 0 -3 0
0 6 0 0 0 0 0 4 0 0
by cofactor expansion.
Answers
1 7 -1 0 -1| = 1(0) - 7(7) - (-1)(0) + 0(0) - (-1)(0) = -48The determinant of the given matrix by cofactor expansion is -48.
To find the determinant of the given matrix using the cofactor expansion, we need to expand it along the first row. Therefore, the determinant is given by:
|1 7 -1 0 -1|
= 1|4 7 0 0| - 7|0 0 -3 0| + (-1)|6 0 0 0|
|0 0 0 0 4| 0
The first cofactor, C11, is determined by deleting the first row and first column of the given matrix and taking the determinant of the resulting matrix. C11 is given by:
C11 = 4|0 -1 0 0| - 0|7 0 0 0| + 0|0 0 0 4| |0 0 0 0|
= 4(0) - 0(0) + 0(0) - 0(0) = 0
The second cofactor, C12, is determined by deleting the first row and second column of the given matrix and taking the determinant of the resulting matrix. C12 is given by:
C12 = 7|-1 0 0 -1| - 0|7 0 0 0| + (-3)|0 0 0 4| |0 0 0 0|
= 7(-1)(-1) - 0(0) - 3(0) + 0(0) = 7
The third cofactor, C13, is determined by deleting the first row and third column of the given matrix and taking the determinant of the resulting matrix. C13 is given by:
C13 = 0|7 0 0 0| - 4|0 0 0 4| + 0|0 0 0 0| |0 0 0 0|
= 0(0) - 4(0) + 0(0) - 0(0) = 0
The fourth cofactor, C14, is determined by deleting the first row and fourth column of the given matrix and taking the determinant of the resulting matrix.
C14 is given by:C14 = 0|7 -1 0| - 0|0 0 4| + 0|0 0 0| |0 0 0|
= 0(0) - 0(0) + 0(0) - 0(0) = 0
The fifth cofactor, C15, is determined by deleting the first row and fifth column of the given matrix and taking the determinant of the resulting matrix. C15 is given by:
C15 = -1|4 7 0| - 0|0 0 -3| + 0|0 0 0| |0 0 0|
= -1(0) - 0(0) + 0(0) - 0(0) = 0
Therefore, we have:|1 7 -1 0 -1| = 1(0) - 7(7) - (-1)(0) + 0(0) - (-1)(0) = -48The determinant of the given matrix by cofactor expansion is -48.
To know more about determinant visit:-
https://brainly.com/question/30970747
#SPJ11
Show that if G is a connected graph, r-regular, is not Eulerian, and GC is connected, then Gº is Eulerian.
Answers
There exists an Eulerian circuit in Gº, and this circuit, together with the paths P(v), forms an Eulerian circuit in G.
Let G be a connected r-regular graph that is not Eulerian, and let GC be a connected subgraph of G.
The graph G – GC has an odd number of connected components since it has an odd number of vertices, and every connected component of G – GC is an irregular graph.
Let v1 be an arbitrary vertex of GC.
For each neighbor v of v1 in G, let P(v) be a path in GC from v1 to v.
The paths P(v) are edge-disjoint since GC is a subgraph of G. Each vertex of G is in exactly one path P(v), since G is connected.
Therefore, the collection of paths P(v) covers all the vertices of G – GC.
Since each path P(v) has an odd number of edges (since G is not Eulerian), the union of the paths P(v) has an odd number of edges.
Thus, the number of edges in GC is even, since G is r-regular.
It follows that Gº (the graph obtained by deleting all edges from G that belong to GC) is Eulerian since it is a connected graph with all vertices of even degree.
Therefore, there exists an Eulerian circuit in Gº, and this circuit, together with the paths P(v), forms an Eulerian circuit in G.
Know more about Eulerian circuit here:
https://brainly.com/question/96508
#SPJ11
Find the average rate of change of the function over the given interval. y=√3x-2; between x= 1 and x=2 What expression can be used to find the average rate of change? OA. lim h→0 f(2+h)-1(2)/h b) lim h→0 f(b) -f(1)/b-1 c) f(2) +f(1)/2+1 d) f(2)-f(1)/2-1
Answers
The correct choice is (c) f(2) + f(1) / (2 + 1). To find the average rate of change of the function y = √(3x - 2) over the interval [1, 2], we can use the expression:
(b) lim h→0 [f(b) - f(a)] / (b - a),
where a and b are the endpoints of the interval. In this case, a = 1 and b = 2.
So the expression to find the average rate of change is:
lim h→0 [f(2) - f(1)] / (2 - 1).
Now, let's substitute the function y = √(3x - 2) into the expression:
lim h→0 [√(3(2) - 2) - √(3(1) - 2)] / (2 - 1).
Simplifying further:
lim h→0 [√(6 - 2) - √(3 - 2)] / (2 - 1),
lim h→0 [√4 - √1] / 1,
lim h→0 [2 - 1] / 1,
lim h→0 1.
Therefore, the average rate of change of the function over the interval [1, 2] is 1.
The correct choice is (c) f(2) + f(1) / (2 + 1).
Learn more about average rate here:
brainly.com/question/13652226
#SPJ11
14. The easiest way to evaluate the integral ∫ tan x dr is by the substitution u-tan x
a. U = cos x.
b. u = sin x
c. u= tan x
Answers
The easiest way to evaluate the integral ∫ tan(x) dx is by the substitution u = tan(x). which is option C.
What is the easiest way to evaluate the integral using substitution method?Let's perform the substitution:
u = tan(x)
Differentiating both sides with respect to x:
du = sec²(x) dx
Rearranging the equation, we have:
dx = du / sec²(x)
Now substitute these values into the integral:
∫ tan(x) dx = ∫ u * (du / sec²(x))
Since sec²(x) = 1 + tan²(x), we can substitute this back into the integral:
∫ u * (du / sec²(x)) = ∫ u * (du / (1 + tan²(x)))
Now, substitute u = tan(x) and du = sec²(x) dx:
∫ u * (du / (1 + tan²(x))) = ∫ u * (du / (1 + u²))
This integral is much simpler to evaluate compared to the original integral, as it reduces to a rational function.
Learn more on integration by substitution here;
https://brainly.com/question/29979533
#SPJ4
"
#16
Question 16 Solve the equation. 45 - 3x = 1 256 O 1) 764 O {3} O {128) (-3) (
Answers
The value of x that satisfies the equation 45 - 3x = 1256 is approximately -403.6666667.
To solve the equation 45 - 3x = 1256, we want to isolate the variable x on one side of the equation. This can be done by performing a series of mathematical operations that maintain the equality of the equation.
Start by combining like terms on the left side of the equation. The constant term, 45, remains as it is, and we have -3x on the left side. The equation becomes:
-3x + 45 = 1256
To isolate the variable x, we need to move the constant term to the right side of the equation. Since the constant term is positive, we'll subtract 45 from both sides of the equation to eliminate it from the left side:
-3x + 45 - 45 = 1256 - 45
Simplifying, we have:
-3x = 1211
To solve for x, we want to isolate the variable on one side of the equation. Since the variable x is currently being multiplied by -3, we can isolate it by dividing both sides of the equation by -3:
(-3x) / -3 = 1211 / -3
The -3 on the left side cancels out, leaving us with:
x = -403.6666667
To know more about equation here
https://brainly.com/question/21835898
#SPJ4
for a one-tailed (upper tail) hypothesis test with a sample size of 18 and a .05 level of significance, the critical value of the test statistic t is
Answers
The critical-value of test statistic "t" for the given one-tailed hypothesis test with a sample size of 18 and a significance level of α = 0.05 is (c) 1.740.
To find the critical-value of the test-statistic "t" for a one-tailed (upper tail) hypothesis-test with a sample-size of 18 and a significance-level of α = 0.05, we use the given information :
Sample-Size (n) = 18
Significance level (α) = 0.05
Since it is a one-tailed (upper tail) test, we find the critical-value corresponding to a cumulative probability of 1 - α = 1 - 0.05 = 0.95.
The degrees of freedom (df) for a one-sample t-test with a sample size of 18 is calculated as (n - 1) = (18 - 1) = 17.
We know that, a 17 degrees-of-freedom and a cumulative probability of 0.95, the critical value of the test statistic "t" is approximately 1.740.
Therefore, the correct option is (c).
Learn more about Critical Value here
https://brainly.com/question/32450122
#SPJ4
The given question is incomplete, the complete question is
For a one-tailed (upper tail) hypothesis test with a sample size of 18 and α = 0.05 level of significance, the critical-value of the test statistic "t" is
(a) 2.110
(b) 1.645
(c) 1.740
(d) 1.734.
:
In a recent year, a research organization found that 241 of the 340 respondents who reported earning less than $30,000 per year said they were social networking users At the other end of the income scale, 256 of the 406 respondents reporting earnings of $75,000 or more were social networking users Let any difference refer to subtracting high-income values from low-income values. Complete parts a through d below Assume that any necessary assumptions and conditions are satisfied a) Find the proportions of each income group who are social networking users. The proportion of the low-income group who are social networking users is The proportion of the high-income group who are social networking usem is (Round to four decimal places as needed) b) What is the difference in proportions? (Round to four decimal places as needed) c) What is the standard error of the difference? (Round to four decimal places as needed) d) Find a 90% confidence interval for the difference between these proportions (Round to three decimal places as needed)
Answers
Proportions of each income group who are social networking users are as follows:The proportion of the low-income group who are social networking users = Number of respondents reporting earnings less than $30,000 per year who are social networking users / Total number of respondents reporting earnings less than $30,000 per year= 241 / 340
= 0.708
The proportion of the high-income group who are social networking users = Number of respondents reporting earnings of $75,000 or more who are social networking users / Total number of respondents reporting earnings of $75,000 or more= 256 / 406
= 0.631
b) The difference in proportions = Proportion of the low-income group who are social networking users - Proportion of the high-income group who are social networking users= 0.708 - 0.631
= 0.077
c) The standard error of the difference = √((p₁(1 - p₁) / n₁) + (p₂(1 - p₂) / n₂))Where p₁ is the proportion of the low-income group who are social networking users, p₂ is the proportion of the high-income group who are social networking users, n₁ is the number of respondents reporting earnings less than $30,000 per year, and n₂ is the number of respondents reporting earnings of $75,000 or more.= √(((0.708)(0.292) / 340) + ((0.631)(0.369) / 406))≈ 0.0339d) The 90% confidence interval for the difference between these proportions is given by: (p₁ - p₂) ± (z* √((p₁(1 - p₁) / n₁) + (p₂(1 - p₂) / n₂)))Where p₁ is the proportion of the low-income group who are social networking users, p₂ is the proportion of the high-income group who are social networking users, n₁ is the number of respondents reporting earnings less than $30,000 per year, n₂ is the number of respondents reporting earnings of $75,000 or more, and z is the value of z-score for 90% confidence interval which is approximately 1.645.= (0.708 - 0.631) ± (1.645 * 0.0339)≈ 0.077 ± 0.056
= (0.021, 0.133)
Therefore, the 90% confidence interval for the difference between these proportions is (0.021, 0.133).
To know more about Proportions visit-
https://brainly.com/question/31548894
#SPJ11
I got P2(x) = 1/2x^2-x+x/2 but I have no idea how to find the error. Could you help me out and describe it in detail?
K1. (0.5 pt.) Let f (x) = |x − 1. Using the scheme of divided differences find the interpolating polynomial p2(x) in the Newton form based on the nodes to = −1, 1, x2 = 3.
x1 =
Find the largest value of the error of the interpolation in the interval [−1; 3].
Answers
The maximum value of the error is 0, and the polynomial P2(x) is an exact interpolating polynomial for f(x) over the interval [-1,3].
To find the error of the interpolation, you can use the formula for the remainder term in the Taylor series of a polynomial.
The formula is:
Rn(x) =[tex]f(n+1)(z) / (n+1)! * (x-x0)(x-x1)...(x-xn)[/tex]
where f(n+1)(z) is the (n+1)th derivative of the function f evaluated at some point z between x and x0, x1, ..., xn.
To apply this formula to your problem, first note that your polynomial is: P2(x) = [tex]1/2x^2 - x + x/2 = 1/2x^2 - x/2.[/tex]
To find the error, we need to find the (n+1)th derivative of f(x) = |x - 1|. Since f(x) has an absolute value, we will consider it piecewise:
For x < 1, we have f(x) = -(x-1).
For x > 1, we have f(x) = x-1.The first derivative is:
f'(x) = {-1 if x < 1, 1 if x > 1}.The second derivative is:
f''(x) = {0 if x < 1 or x > 1}.
Since all higher derivatives are 0, we have:
[tex]f^_(n+1)(x) = 0[/tex] for all n >= 1.
To find the largest value of the error of the interpolation in the interval [-1,3], we need to find the maximum value of the absolute value of the remainder term over that interval.
Since all the derivatives of f are 0, the remainder term is 0.
To know more about polynomial visit:
https://brainly.in/question/9172871
#SPJ11
true or false
dy 6. Determine each of the following differential equations is linear or not. (a) +504 + 6y? = dy 0 d.x2 dc (b) dy +50 + 6y = 0 d.c2 dc (c) dy + 6y = 0 dx2 dc (d) dy C dy + 5y dy d.x2 + 5x2dy + 6y = 0
Answers
The fourth differential equation is nonlinear. In conclusion, the third differential equation, dy/dx + 6y = 0, is linear. The answer is True.
The differential equation, [tex]dy + 6y = 0[/tex], is linear.
Linear differential equation is an equation where the dependent variable and its derivatives occur linearly but the function itself and the derivatives do not occur non-linearly in any term.
The given differential equations can be categorized as linear or nonlinear based on their characteristics.
The first differential equation (a) can be rearranged as dy/dx + 6y = 504.
This equation is not linear since there is a constant term, 504, present. Therefore, the first differential equation is nonlinear.
The second differential equation (b) can be rearranged as
dy/dx + 6y = -50.
This equation is not linear since there is a constant term, -50, present.
Therefore, the second differential equation is nonlinear.
The third differential equation (c) is already in the form of a linear equation, dy/dx + 6y = 0.
Therefore, the third differential equation is linear.
The fourth differential equation (d) can be rearranged as
x²dy/dx² + 5xy' + 6y + dy/dx = 0.
This equation is not linear since the terms x²dy/dx² and 5xy' are nonlinear.
Therefore, the fourth differential equation is non linear.
In conclusion, the third differential equation, dy/dx + 6y = 0, is linear. The answer is True.
To learn more about nonlinear visit;
https://brainly.com/question/25696090
#SPJ11
You are given that cos(A)=−33/65, with A in Quadrant III, and cos(B)=3/5, with B in Quadrant I. Find cos(A+B). Give your answer as a fraction.
Answers
To find cos (A+B), we will use the formula of cos (A+B). Cos (A + B) = cos A * cos B - sin A * sin B
We are given the following information about angles: cos A = -33/65 (in Q3)cos B = 3/5 (in Q1)
As we know that the cosine function is negative in the third quadrant and positive in the first quadrant, thus the sine function will be positive in the third quadrant and negative in the first quadrant.
Thus, we can find the value of sin A and sin B using the Pythagorean theorem:
cos²A + sin²A = 1, sin²A = 1 - cos²Acos²B + sin²B = 1, sin²B = 1 - cos²Bsin A = √(1-cos²A) = √(1-(-33/65)²) = √(1-1089/4225) = √3136/4225 = 56/65sin B = √(1-cos²B) = √(1-(3/5)²) = √(1-9/25) = √16/25 = 4/5
We can now substitute the values of cos A, cos B, sin A, and sin B into the formula of cos (A+B): cos(A+B) = cosA * cosB - sinA * sinB= (-33/65) * (3/5) - (56/65) * (4/5)= (-99/325) - (224/325) = -323/325
Therefore, cos(A+B) = -323/325.
Know more about angles here:
https://brainly.com/question/25716982
#SPJ11
Solve the below equation to find x. 0 x = 6, x=-12 O 0 x = 3 x = 3, x = -6 0 x = 3, x=-12 Clear my choice |2x + 9 = 15 .X
Answers
The solution to the equation 2x + 9 = 15 is x = 3.
What is the value of x in the equation 2x + 9 = 15?In the given linear equation, 2x + 9 = 15, we are tasked with finding the value of x that satisfies the equation. To solve it, we need to isolate the variable x on one side of the equation.
To begin, we subtract 9 from both sides of the equation, which gives us 2x = 15 - 9. Simplifying further, we have 2x = 6.
Next, to solve for x, we divide both sides of the equation by 2. This yields x = 6/2, which simplifies to x = 3.
Learn more about linear equation
brainly.com/question/12974594
#SPJ11
2) Draw contour maps for the functions f(x, y) = 4x² +9y², and g(x, y) = 9x² + 4y². What shape are these surfaces?
Answers
The functions f(x, y) = 4x² + 9y² and g(x, y) = 9x² + 4y² represent ellipsoids in three-dimensional space. Drawing their contour maps allows us to visualize the shape of these surfaces and understand their characteristics.
To draw the contour maps for f(x, y) = 4x² + 9y² and g(x, y) = 9x² + 4y², we consider different levels or values of the functions. Choosing specific values for the contours, we can plot the curves where the functions are equal to those values.
For f(x, y) = 4x² + 9y², the contour curves will be concentric ellipses with the major axis along the y-axis. As the contour values increase, the ellipses will expand outward, representing an elongated elliptical shape.
Similarly, for g(x, y) = 9x² + 4y², the contour curves will also be concentric ellipses, but this time with the major axis along the x-axis. As the contour values increase, the ellipses will expand outward, creating a different elongated elliptical shape compared to f(x, y).
In summary, both f(x, y) = 4x² + 9y² and g(x, y) = 9x² + 4y² represent ellipsoids in three-dimensional space. The contour maps visually illustrate the shape and reveal the elongated elliptical nature of these surfaces.
to learn more about ellipsoids click here:
brainly.com/question/13264495
#SPJ11
Be A^2 = 1
and suppose A=I and
A =-1. (a) Show that the only eigenvalues of A are A = -I
(b) Show that A is diagonalizable.
A(A+1) = A +1, and that A(A – I) = -(A – I) and then look at the nonzero columns of A+1
and of A-I.
Answers
A has two linearly independent eigenvectors and is therefore diagonalizable.
(a)Eigenvalues of A are values λ such that the equation (A − λI) x = 0 has a nonzero solution x. If we use A = I,
then A − λ
I = I − λI
= (1 − λ)I and the equation (A − λI)
x = 0 is equivalent to (1 − λ)x = 0.
Thus λ = 1 is the only eigenvalue of A = I.
If we use A = −1, then A − λI = −1 − λI = (−1 − λ)I and
the equation (A − λI) x = 0 is equivalent to
(−1 − λ)x = 0.
Thus λ = −1 is the only eigenvalue of A = −1.
In both cases the only eigenvalue is A = −I.
(b)To show that A is diagonalizable, we need to show that A has a basis of eigenvectors.
For λ = −1, the equation (A + I) x = 0 is equivalent to
x1 + x2 + x3 = 0, which has a nonzero solution such as
x = (1, −1, 0).
For λ = 1, the equation (A − I) x = 0 is equivalent to
x1 − x2 + x3 = 0, which has a nonzero solution such as x = (1, 1, −2).
Thus A has two linearly independent eigenvectors and is therefore diagonalizable.
To learn more about vectors visit;
https://brainly.com/question/30958460
#SPJ11
Please help!! This is a Sin Geometry question
Answers
In the given diagram, by using trigonometry, the value of sin θ is √5/5. The correct option is D) √5/5
Trigonometry: Calculating the value of sin θFrom the question, we are to determine the value of sin θ in the given diagram
First,
We will calculate the value of the unknown side length
Let the unknown side be x
By using the Pythagorean theorem, we can write that
(5√5)² = 10² + x²
125 = 100 + x²
125 - 100 = x²
25 = x²
x = √25
x = 5
Now,
Using SOH CAH TOA
sin θ = Opposite / Hypotenuse
sin θ = 5 / 5√5
sin θ = 1 / √5
sin θ = √5/5
Hence, the value of sin θ is √5/5
Learn more on Trigonometry here: https://brainly.com/question/20367642
#SPJ1