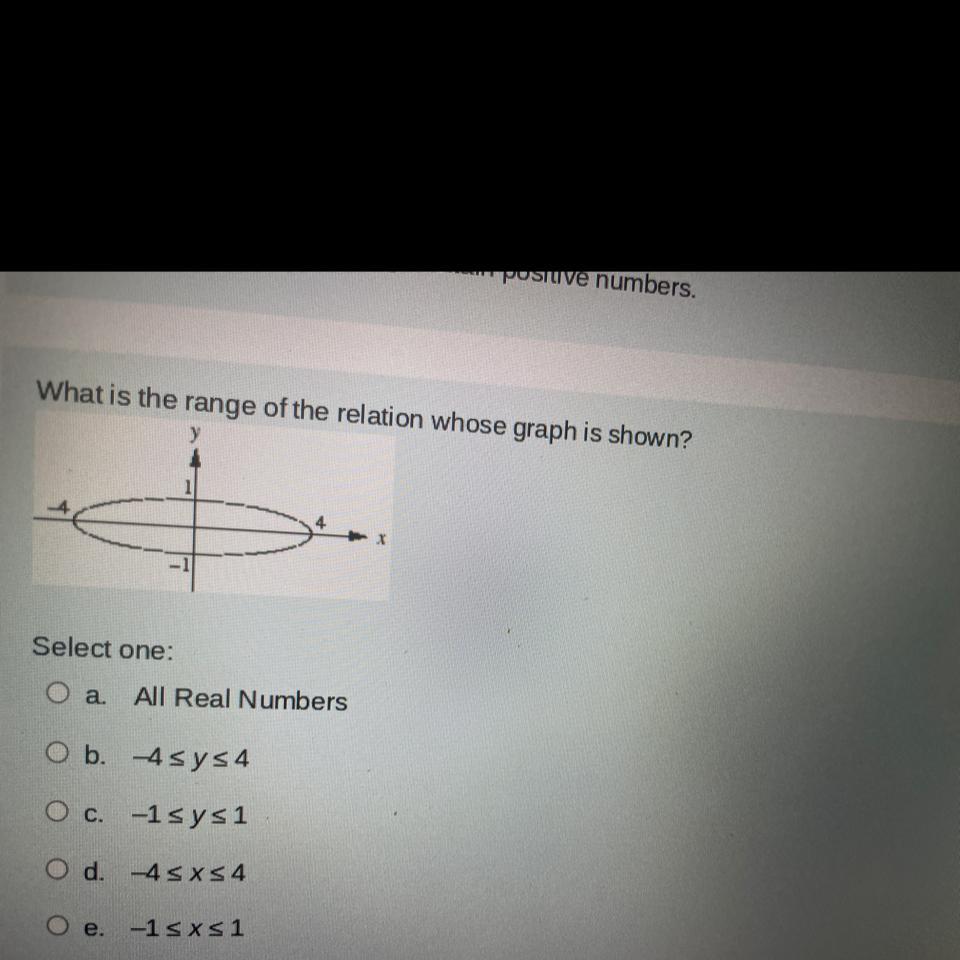
What is the range of the relation whose graph is shown?

Answer: Spheres aren’t three-dimensional—they are two-dimensional. This is evident from the fact that in order to specify a point on a sphere, you only need two pieces of information, such as latitude and longitude.

If you include the interior of the sphere, this is instead called a closed ball, and that is three-dimensional. You can specify a point in the closed ball in all sorts of different ways; one of the most convenient would be latitude, longitude, and distance from the center. However, other than convenience, there is no reason to prefer one coordinate system over any other.

(This fact has nothing to do with spheres or closed balls—that is just a statement that is generally true. People who insist that “the three dimensions” are length, width, and height don’t know what they are talking about.)

Step-by-step explanation:

The probability that a person phones the cable company and waits between 10 to 20 minutes for service is approximately 0.0729, or about 7.29%.

What is the mean and standard deviation?

The standard deviation is a summary measure of the differences of each observation from the mean. If the differences themselves were added up, the positive would exactly balance the negative and so their sum would be zero. Consequently, the squares of the differences are added.

We can start by standardizing the values using the z-score formula:

z = (x - μ) / σ

where:

x = the wait time in minutes

μ = the population mean (average wait time of 28 minutes)

σ = the population standard deviation (5.5 minutes)

For x = 10 minutes:

z = (10 - 28) / 5.5 = -3.27

For x = 20 minutes:

z = (20 - 28) / 5.5 = -1.45

Next, we can use a standard normal distribution table (or a calculator or software) to find the area under the standard normal curve between these two z-scores.

Using a standard normal distribution table, we can find that the area to the left of z = -1.45 is 0.0735, and the area to the left of z = -3.27 is 0.0006. Therefore, the area between z = -3.27 and z = -1.45 is:

0.0735 - 0.0006 = 0.0729

Hence, the probability that a person phones the cable company and waits between 10 to 20 minutes for service is approximately 0.0729, or about 7.29%.

To learn more about the mean and standard deviation visit:

brainly.com/question/475676

#SPJ1

The true statements are:

1. The radius of the circle is 3 units

2. The standard form of the equation is (x-1)^2+y^2=3

3. The center of the circle lies on X-axis

4. The radius of this circle is the same as the radius of the circle whose equation is x^2+y^2=9

The given equation is: x^2+y^2-2x-8=0

The equation in the standard form of the circle can be written as (x-h)^2+(y-k)^2=r^2, where h= center of the circle and r= radius of the circle

The given equation in standard form can be written as

(x^2-2x+1)+y^2-9=0

(x-1)^2+y^2=3^2

Hence from the above equation, the center of the circle is at (1,0) and the radius is 3 units.

To learn more about problems on the equation of a circle refer to:

https://brainly.com/question/23799314?referrer=searchResults

Answer: x = -1 and x = 9

Step-by-step explanation:

Lets solve this equation step by step

1. Simplify both sides of the equation

x^2 - 8x + 16 = 25

2. Subtract 25 from both sides

x^2 - 8x + 16 - 25 = 25 - 25

3. Factor the left side of the equation

(x + 1) (x - 9) = 0

4. Set the factors equal to zero

x + 1 = 0 or x - 9 = 0

Thus your answers are x = -1 and x = 9

You can check by inputting the values into the original equation

(-1 - 4)^2 = 25 and (9 - 4)^2 = 25

Answer: 205.031(nearest thousandth)

or 205.03125

Step-by-step explanation:

Answer:

164 Cakes

Step-by-step explanation:

382 Cakes are made in Week A. This was twice the amount of Week B. 328 divided by two equals 164.

The absolute value equation is:

|x - 15| = 0

We want an absolute value equation that only has the solution x = 15.

So we must have something equal to zero (so we avoid the problem with the signs that we can have with other numbers)

So the equation will be something like:

|x - a| = 0

And the solution is 15, so:

|15 - a | = 0

then a = 15

The equation is:

|x - 15| = 0

Learn more about absolute value:

https://brainly.com/question/1782403

#SPJ1

(1) The value of X is equal to 4  (2) The mean age is 3. (3) The probability of randomly selecting  a child under the age of 9  is approximately 0.83.  

The formula for calculating the average of given numbers is equal to the sum of all values ​​divided by the total number of values. There are three main types of averages: mean, median, and mode. All of these techniques work slightly differently and often give slightly different typical values.

(i). Given that there are a total of 42 children on the birthday, finding the value of x:

2x + 3x (4x-1) + x + (x-2) + (x-3) = 42

11x - 6 = 42

11x = 48

x = 4

Therefore, the value of x is equal to 4.

(ii). To find the average age, we need to calculate the sum of all the ages and divide by the total number of children:

Average age = (7 x 2 + 8 x 3 + 9 x (4-1) +10 x 4 +11 x (4-2) 12 x (4-3)) / 42

 = (14 + 24 + 27 + 40 + 22 +12) / 42

 = 139/42

 = 3.31

Rounded to the nearest whole number, the average age is 3.  

(iii). The probability of randomly selecting  a child under 9 is obtained by adding  the number of children aged 7, 8 or 9 (because we want children under 9) and  dividing by the total number of children:

Number of children under 9 years  = 2x + 3x + (4x-1)

Number of children under 9 years  = 9x - 1

Number of children under 9  = 9(4)–1

Number of children under 9 years  = 35

Probability of choosing a child under 9  = number of children under 9  / total number of children

Probability of choosing a child under 9 = 35/42

The probability of choosing a child under 9 years old is ≈ 0.83

Thus, the probability of randomly selecting  a child under the age of 9  is approximately 0.83.

Learn more about mean, median, and mode here

https://brainly.com/question/30891252

#SPJ1

Since -4 is less than or equal to -2, we use the first part of the definition of f(x) which is f(x) = x + 4 if x ≤ -2. Therefore,

f(-4) = (-4) + 4 = 0.

So, the answer is D. 0.

In 1870, the French writer Jules Verne published his novel "Twenty Thousand Leagues Under the Sea", which tells the story of an underwater adventure aboard the submarine Nautilus.

The novel is considered one of Verne's most popular and well-known works, and it has been translated into many languages and adapted into numerous films, TV shows, and stage productions. "Twenty Thousand Leagues Under the Sea" is known for its imaginative portrayal of futuristic technology, such as the advanced submarine Nautilus, and its detailed descriptions of underwater life and exploration.

Therefore, The novel has also been praised for its themes of adventure, exploration, and the relationship between man and nature. It remains a classic in science fiction and adventure literature, and continues to be read and enjoyed by readers around the world.

To know more about French writer here:

https://brainly.com/question/17460800

#SPJ1

To solve the equation x^2 + 4x - 11 = 0 by completing the square, we can follow these steps:

Move the constant term to the right side of the equation:

x^2 + 4x = 11

Complete the square by adding the square of half the coefficient of x to both sides of the equation:

x^2 + 4x + (4/2)^2 = 11 + (4/2)^2

Simplifying the left side:

x^2 + 4x + 4 = 11 + 4

Factor the perfect square on the left side of the equation:

(x + 2)^2 = 15

Take the square root of both sides of the equation:

x + 2 = ±√15

Solve for x by subtracting 2 from both sides:

x = -2 ± √15

Therefore, the solutions to the equation x^2 + 4x - 11 = 0 by completing the square are x = -2 + √15 and x = -2 - √15.

The principal when making the first payment 51 months later on a private student loan with a principal of $10,000 and a rate of 12.59% would be $15,307.13.

To calculate the principal when making the first payment 51 months later on a private student loan with a principal of $10,000 and a rate of 12.59%, we first need to calculate the amount of interest that has accrued over the 51 months.

Using the formula:

Interest = Principal x Rate x Time

where Principal = $10,000,

Rate = 12.59% per year,

Time = 51/12 years (since the interest is compounded monthly):

Interest = $10,000 x 0.1259 x (51/12)

= $5,307.13

So the total amount owed after 51 months would be:

Total amount owed = Principal + Interest

= $10,000 + $5,307.13

= $15,307.13

Therefore, the principal when making the first payment 51 months later on a private student loan with a principal of $10,000 and a rate of 12.59% would be $15,307.13.

As for recent examples of community change that involves a clash between different cultures that helped disadvantaged communities and the populations, one example is the Black Lives Matter movement, which has brought attention to systemic racism and police brutality in the United States.  Another example is the #MeToo movement, which has raised awareness about sexual harassment and assault and has led to changes in workplace policies and cultural attitudes toward these issues.

Learn more about principal from

https://brainly.com/question/30163719

#SPJ1

The cost of a liter of milk is $2.50 and the cost of a loaf of bread is $2.50.

Cost is the value of goods or services measured in money or other forms of exchange. It is the amount that must be given up in exchange for something else. Costs are typically incurred in the production of goods and services, and can include both tangible and intangible elements, such as labor, materials, overhead, and financing.

The total cost for 3 liters of milk and 5 loaves of bread was $11. Therefore, the cost for 1 liter of milk was ($11 / 3) = $3.67. The cost for 1 loaf of bread was ($11 / 5)
= $2.20.
The total cost for 4 liters of milk and 4 loaves of bread was $10. Therefore, the cost for 1 liter of milk was ($10 / 4) = $2.50. The cost for 1 loaf of bread was ($10 / 4)
= $2.50.
Therefore, the cost of a liter of milk is $2.50 and the cost of a loaf of bread is $2.50.

To learn more about cost
https://brainly.com/question/2292799
#SPJ1

Statistics is a branch of mathematics that involves the collection, analysis, interpretation, presentation, and organization of data. It is used in a wide range of fields such as science, engineering, social sciences, business, economics, and more.

In statistics, data is collected through various methods such as surveys, experiments, and observations. This data is then analyzed using statistical methods to extract meaningful insights, identify patterns and relationships, and make informed decisions.

Some common statistical techniques include descriptive statistics, inferential statistics, hypothesis testing, regression analysis, and probability theory. These techniques are used to help researchers and analysts to understand and draw conclusions about data, and to test whether their conclusions are statistically significant.

Statistics has many practical applications, such as market research, medical research, quality control, risk assessment, and many others. It plays a critical role in modern society, helping individuals and organizations make informed decisions based on data-driven insights.

Learn more about statistic on;

https://brainly.com/question/15525560

#SPJ1

The statistical question that can result in numerical data is "How many hours this week did you spend on homework?"

The statistical question that can result in numerical data is "How many hours this week did you spend on homework?"

This is because the question is asking for a numerical response that can be measured and counted. The other options are not statistical questions that can result in numerical data.

Read more about statistical question at

https://brainly.com/question/22334957

#SPJ1

We find that P(Z > 2.46) is roughly 0.007 using a calculator or a basic normal distribution table. The probability that a bag will contain more than 20% blue jellybeans is therefore approximately 0.007 or 0.7%.

The probability of an event is the ratio of good outcomes to all other potential outcomes. The number of successful outcomes for an experiment with 'n' outcomes can be expressed using the symbol x.

Here in the question,

We can utilise the binomial distribution formula to resolve this issue. In a bag of 200 jelly beans, let X represent the proportion of blue jelly beans. Following that, X exhibits a binomial distribution with parameters of n = 200 and p = 0.15, where p is the likelihood of drawing a blue jellybean.

The formula for determining the likelihood of finding more than 20% blue jellybeans in a bag is:

P (X > 0.2 × 200) = P (X > 40)

Since n is large (200) and p is not too near to 0 or 1, we can utilise the usual approximation to the binomial distribution. We may determine the equivalent mean and standard deviation of the normal distribution by using the mean and variance of the binomial distribution:

μ = np = 200 × 0.15 = 30

σ = √ (np(1-p)) = √ (200 × 0.15 × (1-0.15)) = 4.07

Then, we can standardize the random variable X as:

Z = (X - μ) / σ

So, we have:

P(X > 40) = P((X - μ) / σ > (40 - μ) / σ)

= P(Z > (40 - 30) / 4.07)

= P(Z > 2.46)

We find that P(Z > 2.46) is roughly 0.007 using a calculator or a basic normal distribution table. The likelihood that a bag will contain more than 20% blue jellybeans is therefore approximately 0.007 or 0.7%.

To know more about probability, visit:

https://brainly.com/question/16484393

#SPJ1

The truth table is given above for (A ⋀ B) → C.

What is the logical statement?

A logical statement, also known as a proposition or a statement of fact, is a declarative sentence that is either true or false, but not both. It is a statement that can be evaluated based on the available information or evidence to determine its truth value. In other words, a logical statement is a statement that can be either true or false, but not both.

To create a truth table for the logical statement (A ⋀ B) → C, we need to consider all possible combinations of truth values for propositions A, B, and C.

There are 2 possible truth values (true or false) for each proposition, so there are 2³ = 8 possible combinations.

We can organize these combinations into a table as follows:

| A | B | C | (A ⋀ B) | (A ⋀ B) → C |

|---|---|---|---------|-------------|

| T | T | T |    T    |      T      |

| T | T | F |    T    |      F      |

| T | F | T |    F    |      T      |

| T | F | F |    F    |      T      |

| F | T | T |    F    |      T      |

| F | T | F |    F    |      T      |

| F | F | T |    F    |      T      |

| F | F | F |    F    |      T      |

In this table, the column labeled (A ⋀ B) represents the truth value of the conjunction of A and B (i.e., A AND B), and the column labeled (A ⋀ B) → C represents the truth value of the conditional statement (A ⋀ B) → C.

The symbol "T" represents "true" and the symbol "F" represents "false".

Hence, The truth table is given above for (A ⋀ B) → C.

To learn more about the logical statement visit:

https://brainly.com/question/29021787

#SPJ1

Answer: The altitude of the triangle is [tex]h = 7 \sqrt{3}.[/tex]

Step-by-step explanation:

Suppose that we separate the equilateral triangle with the altitude of the triangle, as shown in the diagram I attached.

Then the length of the altitude [tex]h[/tex] can be found through the Pythagorean theorem:

[tex]h = \sqrt{14^2-\left( \frac{14}{2} \right)^2} = \sqrt{147} = \boxed{7 \sqrt{3}}.[/tex]

Therefore, the altitude of the equilateral triangle is [tex]h = 7 \sqrt{3}.[/tex]

Answer:

(x - 5)² + (y + 6)² = 16

Step-by-step explanation:

assuming you require the equation of the circle

the equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k ) are the coordinates of the centre and r is the radius

here (h, k ) = (5, - 6 ) and r = 4 , then

(x - 5)² + (y - (- 6) )² = 4² , that is

(x - 5)² + (y + 6)² = 16

The number of cups of vegetable oil used by Colin to make 8 cakes is given by A = 5 1/3 cups

Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.

It demonstrates the equality of the relationship between the expressions printed on the left and right sides.

Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.

Given data,

Let the equation be represented as A

Now, the value of A is

Substituting the values in the equation, we get

Let the number of cups of vegetable oil used by Colin to make 8 cakes be represented as A

Now , the number of cups of vegetable oil used by Colin to make 1 cake is given by = ( 2/3 ) cups of oil

And , number of cups of vegetable oil used by Colin to make 8 cakes A =

A = 8 x number of cups of vegetable oil used by Colin to make 1 cake

On simplifying the equation, we get

[tex]\text{A} = 8 \times \huge \text{(} \dfrac{2}{3} \huge \text{)}= \dfrac{16}{3}[/tex]

[tex]\boxed{\bold{A = 5 \dfrac{1}{3} \ cups}}[/tex]

Therefore, the value of A is 5 1/3 cups

Hence, the number of cups of vegetable oil required is 5 1/3 cups

To learn more about equations click:

brainly.com/question/19297665

Complete question is-

Colin uses 2/3 cup of vegetable oil in each cake that he makes for his father's bakery.

If Colin made 8 cakes, how much oil did Colin use in all?

A. 5 1/3 cups

B. 7 1/3 cups

C. 8 2/3 cups

D. 16 1/3 cups​

From the data in the table, we can conclude that when x = 4, then the residual will equal -1.

To determine the residual, we can begin by obtaining the difference between the given and the predicted values of y.

So, Residual = Gven value - Predicted value.

When x = 4 in the table, Given value is 9 and predicted value is 10. So, 9 - 10 = -1. So, we can say that the residual value is -1.

Learn more about residual values here:

https://brainly.com/question/30243740

#SPJ1

Answer:

The residual is the difference between the actual y-value and the predicted y-value on a regression line. Since no table or equation is provided, we cannot calculate the exact residual. However, I can explain the concept to you.

Step-by-step explanation:

In general, to calculate the residual, we would need a regression equation or a line of best fit. This equation allows us to predict the y-values for different x-values. Then, we can compare the predicted values to the actual values given in the table to find the residuals.

If you have the regression equation or the line of best fit, I can help you calculate the residual for a specific x-value.

Answer: Using the formula i = prt, we have:

i = (104292.12 - 80040) = 24252.12

p = 80040

t = 3

Substituting these values, we get:

24252.12 = 80040 * r * 3

Solving for r, we get:

r = 0.101 or 10.1%

Therefore, the interest rate is 10.1%.

Step-by-step explanation:

Answer:

Step-by-step explanation:

2.1 so a

Answer:

the answer is 110-23i

The diameter of the semicircle is with an area of 76.97 square yards is 14 yards.

Semicircle is half that of a circle, hence the area will be half that of a circle. Area of semi circle = 1/2 × πr²

Where r radius and π is constant pi.

Since we are given the area of the semicircle as 76.97 square yards, we can set up the following equation:

76.97 = 1/2 × (πr²)

Multiplying both sides by 2, we get:

153.94 = πr²

Dividing both sides by π, we get:

r² = 49

Taking the square root of both sides, we get:

r = 7

Therefore, the diameter of the semicircle is: d = 2r  = 2(7) = 14 yards

Learn more about area of circles here: brainly.com/question/11952845

#SPJ1

The standard form equation of a circle whose diameter endpoints are  (-3,4) (2,1) is [tex](x - (-0.5))^2 + (y - 2.5)^2[/tex] = 6.5

The general form of the equation of a circle is (x - h)² + (y - k)² = r², where (h, k) represents the center of the circle and r represents the radius. This equation is derived using the Pythagorean theorem, which states that the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse. By setting (x - h)² and (y - k)² equal to r² and then combining the two equations, we get the standard form equation of a circle.

The center of the circle lies in the middle of the diameter, so we find the midpoint of the end points:

[tex](\frac{-3+2}{2} , \frac{4+1}{2} )[/tex] = (-0.5, 2.5)

And radius of the circle is half of the diameter, which is:

[tex]\frac{\sqrt{( 2-(-3))^2 + (1-4)^2 )}}{2}[/tex] = [tex]\frac{\sqrt{26}}{2}[/tex]

Therefore, the circle equation is:

[tex](x - (-0.5))^2 + (y - 2.5)^2[/tex] = [tex](\frac{\sqrt{26} }{2} )^2[/tex] = 26/4 = 6.5

[tex](x - (-0.5))^2 + (y - 2.5)^2[/tex] = 6.5

To know more about circle equation visit:

brainly.com/question/29288238

#SPJ1

We can show by the uniqueness theorem that the linear transformation, Y = aX + b, is also a normal random variable because the resultant probaility density fnction of Y equals: f(y) = (1/√(2πa^2σX^2)) * exp(-(y-aμX-b)^2/(2a^2σX^2)).

To show that the linear transformation, Y = aX + b is a normal random variable, we need to demonstrate that it satisfies the properties of a normal distribution. This means that it should have a bell-shaped probability density function, mean, and variance.

We can prove that it meets the mean condition this way:

E(Y) = E(aX + b) = aE(X) + b = aμX + b

Next, we can prove that it meets the variance condition thus:

Var(Y) = Var(aX + b) = a^2Var(X) = a^2σX^2

Lastly, the probability density function is given as f(y) = (1/√(2πa^2σX^2)) * exp(-(y-aμX-b)^2/(2a^2σX^2)). This proves that the conditions for a normal random variable is met.

Learn more about a normal random variable here:

https://brainly.com/question/29360240

#SPJ1

Jackson's total cost after the discount and before tax would be $24.67.

When a store offers a discount, it reduces the price of the item by a certain percentage. In this case, Jackson has a loyalty card that gives him a 10% discount on his purchase.

To calculate the price after the discount, we multiply the original price by 1 minus the discount percentage (in decimal form).

Here we have

Jackson has a 10% discount at his local hardware store.

Let 'x' be the cost before tax

After a 10% discount,

The amount that Jackson could pay 90% of the cost

Given that he wants to buy $ 27.40  

The cost of items after discount = 90% of 27.40

= [ 90/100 ] × 27.40

= [ 0.9 ] × 27.40

= 24.66

Therefore,

Jackson's total cost after the discount and before tax would be $24.67.

Learn more about Discounts at

https://brainly.com/question/30814332

#SPJ9