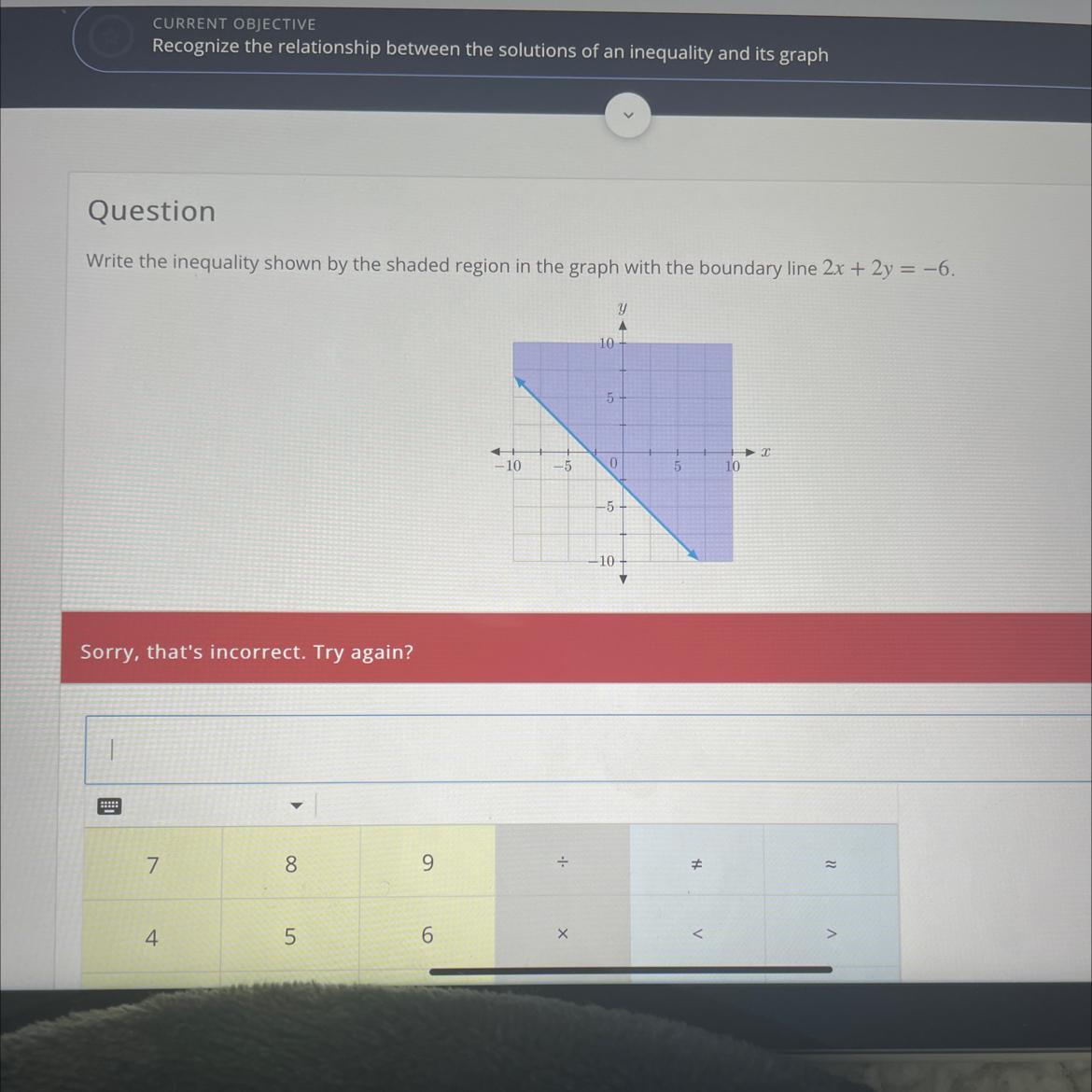
Write the inequality shown by the shaded region in the graph with the boundary line 2x + 2y = -6
Answers
The Solution:
Given the equation of a line below:
[tex]2x+2y=-6[/tex]Step 1:
We shall determine the x-intercept and y-intercept of the given line.
x-intercept: The value of x when y=0
[tex]\begin{gathered} \text{When y=0} \\ 2x+2(0)=-6 \\ 2x=-6 \end{gathered}[/tex]Dividing both sides by 2, we get
[tex]\begin{gathered} x=\frac{-6}{2}=-3 \\ \text{ So,} \\ \text{ The x-intercept = (-3,0)} \end{gathered}[/tex]Similarly,
y-intercept: the value of y when x=0
[tex]\begin{gathered} 2(0)+2y=-6 \\ \\ 2y=-6 \end{gathered}[/tex]Dividing both sides by 2, we get
[tex]\begin{gathered} y=\frac{-6}{2}=-3 \\ \text{ hence,} \\ \text{ The y-intercept = (0,-3)} \end{gathered}[/tex]Determine the inequality symbol that will be used to replace the equality sign.
If the straight line is unbroken, it means the points on the line are inclusive. So, the inequality symbol will not be a strict inequality. It will be one of these two inequalities:
[tex]\leq\text{ or }\ge[/tex]Determine the exact inequality symbol that will represent the shaded region.
If the shaded region is below the line, the correct inequality will be:
[tex]\leq[/tex]But where the shaded region is above the line, the correct inequality symbol will be:
[tex]\ge[/tex]From the given graph, it is clear that the shaded region is above the line. So, it follows that the correct inequality is:
[tex]\ge[/tex]Therefore, the correct answer is:
[tex]2x+2y\ge-6[/tex]Related Questions
In may 2020, there were 2,119,800 people in the available labor force in oregon. the unemployment rate in oregon for may 2020 was 14.2%. determine the number of people who were unemployed in oregon during may 2020. round your answer to the nearest whole number.
Answers
301,012
1) Considering the data, we can write out the following equivalence:
[tex]\begin{gathered} 2,119,800---100\% \\ x--------14.2\% \end{gathered}[/tex]2) Notice that we need to rewrite those figures as 100% =1, and 14.2% as 0.142.
Now we can calculate how many people are equivalent to that rate of unemployment:
[tex]\begin{gathered} \frac{2119800}{x}=\frac{1}{0.142} \\ x=2119800\cdot0.142 \\ x=301,011.6\approx301,012 \end{gathered}[/tex]Notice that we rounded off to the nearest whole number.
3) So, there were approximately 301,012 Oregonians unemployed at that time
help me pleaseeeeeeeee
Answers
The values of given functions f(-2), f(0) and f(7) when f(x) = 1-6x are 13, 1 and -41 respectively.
According to the question,
We have the following function:
f(x) = 1-6x
Now, we can find the values of each function by putting the numbers in place of x.
Now, in order to find the value of f(-2), we will put -2 in place of x in the given function.
f(-2) = 1-6*(-2)
f(-2) = 1+12
f(-2) = 13
Now, in order to find the value of f(0), we will put 0 in place of x in the given function.
f(0) = 1-6(0)
f(0) = 1-0
(We know that when a number is multiplied with 0 then the result is always 0.)
f(0) = 1
Now, in order to find the value of f(7), we will put 7 in place of x in the given function.
f(7) = 1-6*7
f(7) = 1-42
f(7) = -41
Hence, the values of f(-2), f(0) and f(7) are 13, 1 and -41 respectively.
To know more about values here
https://brainly.com/question/13581879
#SPJ1
The half-life of a radioactive kind of iodine is 21 hours. How much will be left after 42 hours,if you start with 19,296 grams of it?In grams
Answers
The half-life of a radioactive material is the time that it takes to reduce to half
In this case, the half-life is 21 hs, and since 42hs is twice the half-life, the material will reduce to half after 21 hours and then to half again.
one half of one half is:
[tex]\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}[/tex]Then we multiply by the initial amount:
[tex]19,296\cdot\frac{1}{4}=4824gr[/tex]The amount left after 42 hours is 4824 grams.
The diagram shows two similar polygonsN51P224048MR3016.5SFigures not drawn to scale.What is the length of CS?
Answers
Notice the correspondence between the vertices of the polygons:
[tex]VQRGX\approx CNPMS[/tex]Corresponding segments of similar polygons are proportional. Then:
[tex]\frac{CS}{VX}=\frac{PM}{RG}[/tex]Substitute VX=48, PM=22 and RG=16.5 and solve for CS:
[tex]\begin{gathered} \Rightarrow\frac{CS}{48}=\frac{22}{16.5} \\ \Rightarrow CS=\frac{22}{16.5}\times48 \\ \Rightarrow CS=64 \end{gathered}[/tex]Therefore, the length of CS is 64.
A right triangle is shown in the figure what is the value of x
Answers
So,
We could use the pythagorean theorem as follows:
[tex](3x)^2+x^2=(\sqrt[]{40})^2[/tex]And then solve for x:
[tex]\begin{gathered} 10x^2=40 \\ x^2=\frac{40}{10} \\ x^2=4 \\ x=2 \end{gathered}[/tex]Therefore, x=2.
I wonder what I’m doing wrong ?
P^2-10p+16=1+6p
Answer is (15,1)
But I can’t seem to figure it out.
Answers
Steps to Solve:
1. Collect like terms
2. Factor quadratic
3. solve for p
Factoring a Quadratic where a = 1
1. find two numbers that are the product of ac and the sum of b
2. set up the two linear terms with the variable associated with a
2. insert the values found in step 1 into parentheses
1. collect like terms
[tex]p^2-10p-6p+15-1=0[/tex]
[tex]p^2-16p+15 = 0[/tex]
2. Factor quadratic
ac = 15 and b =-16, two numbers that multply to ac and are the sum of b are -15 and 1[tex](p-15)(p-1)=0[/tex]
2 solutions can be found[tex]p-15=0[/tex] OR [tex]p-1=0[/tex]
[tex]p= 15[/tex] [tex]p=1[/tex]
have $100 to spend on Halloween candy. A pack of M&Ms cost $3.50. 15 Twix bars cost $7.00. 9 Hershey Bars cost $3.00. If I need 15 M&M packs, 17 Twix bars and 9 Hershey bars how much will it cost? How much money will I have left?
Answers
Answer:
Assuming this is rounding to the nearest cent, $36.51
Step-by-step explanation:
1 ) Find the cost of each individual candy.
M&Ms are given at $3.50 per pack.
To find the cost of one Twix bar, divide $7.00 by 15. This makes Twix equal $0.47 per bar.
You don't need to find the individual price of the Hershey's bars because 9 bars cost $3.00 and you need 9 bars in the equation.
2 ) Now that you have the prices you need, multiply.
For M&Ms 15 x $3.50 = $52.50
For Twix 17 x $0.47 = $7.99
For Hershey's, it is given that 9 bars are $3.00
3 ) Add all of these up to get the total spent on candy.
$52.50 + $7.99 + $3.00 = $63.49
4 ) Subtract this from the budget to get the total amount left over.
$100 - $63.49 = $36.51
can you explain this to me what you are supposed to do this
Answers
Solution
If we see the two tirangles given BAC and A'B'C' we can conclude that we have the following congruent angles
< CAB = < C'A'B'
< BCA = < B'C'A'
< ABC = < A'B'C'
Solving a Debra, Ravi, and Ahmad sent a total of 76 text messages during the weekend. Ahmad sent 2 times as many messages as Ravi. Debra sent 8 more messages than Ravi. How many messages did they each send?
Answers
Let the number of messages sent by Ravi be x.
Ahmad sent 2 times as many messages as Ravi. Therefore, Ahmad sent 2x messages.
Debra sent 8 more messages than Ravi. Therefore, Debra sent (x + 8) messages.
The sum of all the messages is 76:
[tex]x+2x+x+8=76[/tex]Solving for x, we have:
[tex]\begin{gathered} 4x+8=76 \\ 4x=76-8 \\ 4x=68 \\ x=\frac{68}{4} \\ x=17 \end{gathered}[/tex]The number of messages Ahmad sent will be:
[tex]2(17)=34[/tex]The number of messages Debra sent will be:
[tex]17+8=25[/tex]ANSWER
[tex]\begin{gathered} Debra\to25\text{ }messages \\ Ravi\to17\text{ }messages \\ Ahmad\to34\text{ }messages \end{gathered}[/tex]Not a timed or graded assignment. Need a quick answer tho. Thank you
Answers
ANSWER:
Difference of squares
[tex]8x-7[/tex]STEP-BY-STEP EXPLANATION:
We have the following quotient:
[tex]\frac{64x^2-49}{8x+7}[/tex]We factor, knowing that the numerator is a difference of squares, therefore:
[tex]\begin{gathered} a^2-b^2=(a+b)(a-b) \\ \text{ in this case} \\ a=8x \\ b=7 \\ 64x^2-49=(8x+7)(8x-7) \\ \text{ Replacing:} \\ \frac{(8x+7)(8x-7)}{8x+7}=8x-7 \end{gathered}[/tex]Jack scored 80 out of 85 points on a recent test. What is his score as a percent, rounded to the nearest whole percent?
Answers
jack scored = 80
total point = 85
so the percentage is,
[tex]=\frac{80}{85}\times100[/tex][tex]\begin{gathered} =\frac{8000}{85} \\ =94.11\text{ \%} \end{gathered}[/tex]thus, the nearest whole percentage is 94 %
You invent a game that is played on a perfect 12 foot by 12 foot square. What is the longest distance between any two points on the square? A. 12 feetB. 15 feetC. 17 feetD. None of the aboveI will really appreciate the help on this problem.
Answers
The given figure is a square that measures 12 foot by 12 foot. please see illustration below;
The square in the sketch above shows the longest distance between two opposite diagonals, and that is the hypotenuse, labelled as a.
In the triangle ADC, using Pythagoras' theorem;
[tex]\begin{gathered} AD^2+DC^2=AC^2 \\ 12^2+12^2=a^2 \\ 144+144=a^2 \\ 288=a^2 \\ \sqrt[]{288}=a \\ a=16.97 \end{gathered}[/tex]The longest distance which is a (that is AC) is approximately 17 ft as shown above (16.97 ft).
Solve for x: 3x + 2 = 11 A : 11/5 B: 3. C : 11/3. D : 13/3. E : 6
Answers
Explanation:
The equation is given as:
3x + 2 = 11
The first step is to collect like terms ( Note that if 2 crosses to the other side of the equality sign, it becomes -2)
3x = 11 - 2
3x = 9
The next step is to divide both sides by 3:
3x/3 = 9/3
x = 3
Hello I need help with this question as fast as possible please , I am on my last few questions and I have been studying all day for my final exam for math tomorrow. It is past my bed time and I am exhausted . Thank you so much for understanding:))
Answers
Notice that:
[tex]665.6=10.4\times64.[/tex]Therefore, if we divide the resulting equation of step 3 by 10.4 we get:
[tex]\begin{gathered} \frac{10.4x}{10.4}=\frac{665.6}{10.4}, \\ x=64. \end{gathered}[/tex]Then the missing step is:
Divide both sides of the equation by 10.4.
Answer: Last option.
Area of a sector A sector with a radius of \maroonD{8\,\text{cm}}8cmstart color #ca337c, 8, start text, c, m, end text, end color #ca337c has an area of \goldE{56\pi\,\text{cm}^2}56πcm
Answers
To find the angle of the sector, follow the steps below.
Step 01: Find the total area of the circle.
The area (A) of a circle with radius r is:
[tex]A=\pi r^2[/tex]Knowing that r = 8 cm, then the area is:
[tex]\begin{gathered} A=8^2\pi \\ A=64\pi\text{ cm}^2 \end{gathered}[/tex]Step 02: Find the central angle.
To find the angle, use proportions.
Knowing that:
When angle = 2π, A = 64π,
Then when angle is x, A = 56π
[tex]\begin{gathered} \frac{x}{2\pi}=\frac{56\pi}{64\pi} \\ \\ \text{ Multiplying both sides by 2}\pi: \\ \frac{x}{2\pi}*2\pi=\frac{56\pi}{64\pi}*2\pi \\ x=\frac{56*2}{64}\pi \\ x=\frac{112}{64}\pi \\ \\ \text{ Dividing both the numerator and the denominator by 16:} \\ x=\frac{\frac{112}{16}}{\frac{64}{16}}\pi \\ x=\frac{7\pi}{4} \end{gathered}[/tex]Answer: The central angle measure is:
[tex]\frac{7\pi}{4}[/tex]At a local school, 164 students play soccer and 112 students play baseball. What is the ratio of soccer players to baseball players?41:2828:4113:2828:13
Answers
Given
The number of students who play soccer is 164.
The number of students who play baseball is 112
Explanation
To find the ratio of soccer player to baseball players .
Divide the number of soccer player by the number of baseball player.
[tex]\frac{164}{112}=\frac{41}{28}[/tex]Answer
Hence the ratio of soccer players to baseball players is
[tex]41:28[/tex]Express y in terms of x. Then find the value of y when x= -1-3 (x + 2) = 5yY in terms of x:Y=
Answers
LEt's express y in term of x:
[tex]\begin{gathered} -3(x+2)=5y \\ y=\frac{-3(x+2)}{5} \end{gathered}[/tex]Therefore:
[tex]y=-\frac{3}{5}x-\frac{6}{5}[/tex]Now, if x=-1, then we have:
[tex]\begin{gathered} y=-\frac{3}{5}(-1)-\frac{6}{5} \\ =\frac{3}{5}-\frac{6}{5} \\ =-\frac{1}{5} \end{gathered}[/tex]Therefore, if x=-1 then y=-1/5
2. Graph the image of Parallelogram WXYZ under a translation 4 units to the left and 6 units up
Answers
Translation 4 units to the left transforms the point (x, y) into (x-4, y). Applying this rule to the parallelogram WXYZ, we get:
W(0, -2) → (0-4, -2) →W'(-4, -2)
X(2, -2) → (2-4, -2) → X'(-2, -2)
Y(2, -5) → (2-4, -5) → Y'(-2, -5)
Z(0, -5) → (0-4, -5) → Z'(-4, -5)
Translation 6 units up transforms the point (x, y) into (x, y+6). Applying this rule to the parallelogram W'X'Y'Z', we get:
W'(-4, -2) → (-4, -2+6) → W''(-4, 4)
X'(-2, -2) → (-2, -2+6) → X''(-2, 4)
Y'(-2, -5) → (-2, -5+6) → Y''(-2, 1)
Z'(-4, -5) → (-4, -5+6) → Z''(-4, 1)
Where the parallelogram W''X''Y''Z'' is the image of Parallelogram WXYZ translated 4 units to the left and 6 units up, as can be seen in the next graph:
Ms. Morgan is the cafeteria manager. She keeps track of how many students select each type of drink. Today during breakfast, 32 children picked milk while 44 children picked juice. What is the ratio of the numbe of children who picked juice to those who picked milk?
Answers
Answer:
ratio of those who picked juice to milk
it refers to division
To produce a textbook, suppose the publisher spent $110,000 for typesetting and $7.50 per book for printingand binding. The total cost to produce and print n books can be written asC = 110,000+ 7.51a. Suppose the number of books printed in the first printing is 10,000. What is the total cost?The total cost is $b. If the average cost is the total cost divided by the number of books printed, find the average cost of producing10,000 textbooks.The average cost of producing 10,000 textbooks is $c. Find the cost to produce one more textbook when you have already produced 10,000 textbooks.If you have already produced 10,000 textbooks, it'll cost you $ to produce one more.
Answers
The given equation is
[tex]C=110000+7.5n[/tex]a)
The number of books=10000
Substitute n=10000 in the given equation, we get
[tex]C=110000+7.5\times10000[/tex][tex]C=185000[/tex]The total cost is $185,000.
b)
[tex]\text{Average cost =}\frac{185000}{10000}=18.5[/tex]The average cost of producing 10,000 textbooks is $18.5.
c)
If we need to produce one more after producing 10000 books.
substitute n=10001 in the given equation, we get
[tex]C=110000+7.5(10001)=185007.5[/tex][tex]\text{One book cost after printed 10000 book=cost of 10000 books-cost of 10001 books}[/tex][tex]\text{One book cost after printed 10000 book=1}85000-185007.5=7.5[/tex]
If you have already produced 10,000 textbooks, it'll cost you $7.5 to produce one more.
how do i solve the equation?
Answers
Answer: 7x=63 and 12x+9= 117
Step-by-step explanation:
add those two equations and set it to 180 degree
7x+12x+9=180
19x=171
x= 9
7x = 7 (9) = 63
12x+9 = 12 (9)+9 = 117
Tell whether the triangle with the given side lengths is a right triangle. 18, 80, 82 Write the pythagorean theorem Substitute the values from the triangle in the equation then solve If both side of the equation is the same then yes the triangle is right triangle. Il both sides are different then no the triangle is not a right triangle
Answers
Pythagorean theorem :
c^2 = a^2 + b^2
Where:
c = hypotenuse (the longest side ) = 82
A & b = the other 2 sides (18 and 80)
Replacing:
82^2 = 80^2 + 18^2
Solve:
6,724 = 6,400+ 324
6,724 = 6,724
Both sides of the equations are equal. IT is a right triangle
Given that events A and B are independent with P(A) = 0.08 and P(B) = 0.25,determine the value of P(A and B), rounding to the nearest thousandth, ifnecessary.
Answers
To find: P(AandB)
P(AandB)=P(A)*P(B)
P(AandB)=0.08*0.25
P(AandB)=0.02
Thus the required answer is 0.02
heyy could you help me out with this problem I'm stuck
Answers
Since congruent angles are equal
Therefore the two figures are similar
we have
9 / 9 = 2x / x + 4
introduce cross multiplication
9 (2x) = 9(x + 4)
18x = 9*x + 9*4
18x = 9x + 36
collect the like terms
18x - 9x = 36
9x = 36
divide boths sides by 9
9x / 9 = 36/9
x = 4
The first missing variable is 2x
2 x 4
= 8
The second is x + 4
we have 4 + 4
= 8
m
plant A produced 3 times as many panels as plant b. two percent of the panels from plant A and 5% of the panels from plant b were defective. how many panels did plant b produce if the two plants together produced 990 defective panels
Answers
let x the number of panels that Plant A produced
y the number of panels that Plant B produced
then, we have
x = 3y
0.02x + 0.05y = 990
and solve the system:
[tex]\begin{gathered} 0.02(3y)+0.05y=990 \\ 0.06y+0.05y=990 \\ 0.11y=990 \\ \frac{0.11y}{0.11}=\frac{990}{0.11} \\ y=9000 \end{gathered}[/tex]answer: plant b produced 9000 panels
Solve by using a proportion. Round answers to the nearest hundredth if necessary. 1. You jog 3.6 miles in 30 minutes. At that rate, how long will it take you to jog 4.8 miles? 2. You earn $33 in 8 hours. At that rate, how much would you earn in 5 hours?
Answers
EXPLANATION
Let's see the facts:
rate ---> 3.6 miles / 30 minutes
The unit rate is:
Unit rate = 0.12 miles/minute
Now, dividing the needed 4.8 miles by the unit rate will give us our desired number:
Time= 4.8 miles/ 0.12miles/minute = 40 minutes
The answer is 40 minutes.
Write a relation consisting of five ordered pairs that satisfies the following conditions. The relation is a function. Switching the x- and y-coordinates of each ordered pair results in a relation that is not a function.
Answers
Answer:
Step-by-step explanation:
If each value of x only has one corresponding value of y, it is a function. You can test this just by eye or by graphing and doing the vertical line test by rolling a pencil or other straight object across to make sure only one point is on the line at a time
y = (x+3)^3 find the zeros of each function
Answers
Given,
[tex]y=(x+3)^3[/tex]We have,
[tex]y=0[/tex]when,
[tex]\begin{gathered} x+3=0 \\ \Rightarrow x=-3 \end{gathered}[/tex]The zeros of the function are x=-3,-3,-3
* The functions f(x) and g(x) are both linear. f(2) = 4 and f(3) = -1, while g(2) = 6 and g(-3) = 7. Are these lines parallel, perpendicular, or neither? Show your work algebraically.
Answers
Solution
f(2) = 4 and f(3) = -1
g(2) = 6 and g(-3) = 7
From the info given we can see this :
x = 2 f(2) = 4 , g(2)= 6
x= 3 f(3)= -1 , g(3)= 7
And we can calculate the slope with the following formula:
[tex]m=\frac{-1-4}{3-2}=-5[/tex][tex]m=\frac{7-6}{3-2}=1[/tex]And for this case we can conclude that the lines are neither
Since m1 is different from m2
And m1*m2 is not -1
A random number generator is used to select an integer from 1 to 100 (inclusively). What is the probability of selecting the integer 730?
Answers
If a random number generator is used to select an integer from 1 to 100, then the probability of selecting the integer 730 is zero.
Here a random number generator is used to select an integer from 1 to 100.
Therefore the range of the outcome = 1 to 100
Here we have to find the probability of selecting the integer 730
The probability = Number of favorable outcomes / Total number of outcomes.
Here a random number generator is used to select an integer from 1 to 100, but the given number is 730 which is out of range. Therefore the probability is zero
Hence, if a random number generator is used to select an integer from 1 to 100, then the probability of selecting the integer 730 is zero.
Learn more about probability here
brainly.com/question/11234923
#SPJ1