Answers
Answer:
1. 90
2. 468
Step-by-step explanation:
Answer:
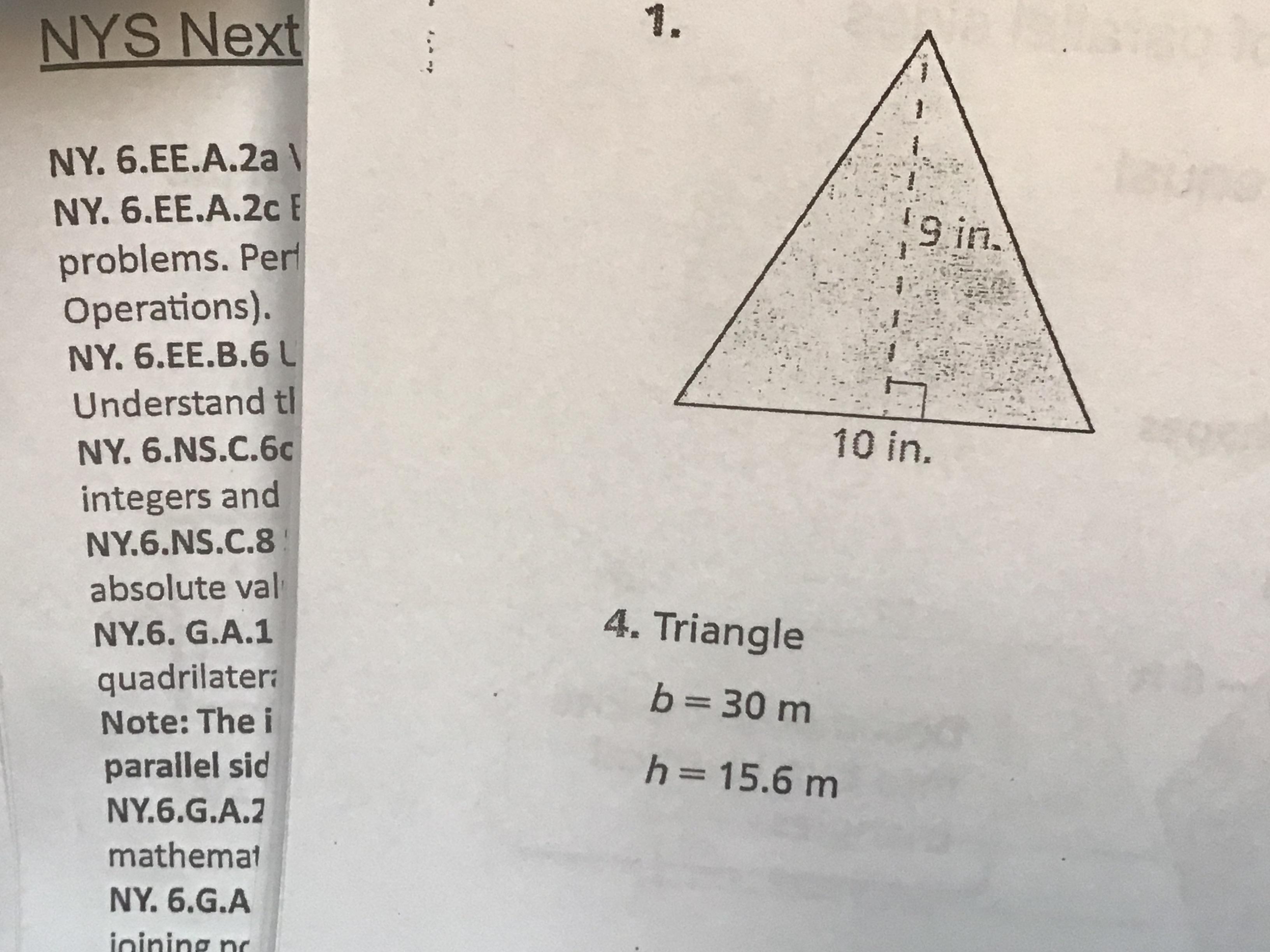
Question 1). 45 in
Question 2). 234 m
Step-by-step explanation:
Area = base x height x 1/2
10 x 9 = 90
90 x 1/2 = 45
Question 2)
30 x 15.6 = 468
468 x 1/2 = 234 m
Related Questions
Let's get this party started!
Warm Up Time!
Graph a relationship in which the value of y is 5 less than half the value of x.
Select two points on the coordinate grid. A line will connect the points.
2
3
Step 1: Write the equation (Translate from
words to a number sentence)
Step 2: Graph using Slope Intercept Form
What is the Y-intercept? Plot this point first!
What is the slope? Use the slope to plot a 2nd point
Answers
The slope of the equation is 1/2 and the y-intercept is -5.
What is the slope?
The slope of a line is a measure of its steepness. Mathematically, the slope is calculated as "rise over run" (change in y divided by change in x).
Step 1:
The relationship between x and y can be expressed as:
y = (1/2)x - 5
This equation says that y is equal to half of x, with 5 subtracted from that value.
Step 2:
To graph this equation using the slope-intercept form (y = mx + b), we can identify the slope and y-intercept.
The slope of the equation is 1/2, which means that for every increase of 1 unit in x, y increases by 1/2 unit.
The y-intercept is -5, which is the point where the line crosses the y-axis.
To graph the equation, we can start by plotting the y-intercept, which is the point (0, -5).
Next, we can use the slope to find another point on the line. Since the slope is 1/2, we can move up 1 unit and right 2 units (since the slope is rise over run, or change in y over change in x). This gives us the point (2, -4).
We can now draw a line that connects these two points, which represents the relationship between x and y.
The two points are:
(0, -5)
(2, -4)
The graph of the equation is in the attached image.
Hence, The slope of the equation is 1/2 and the y-intercept is -5.
To learn more about the slope visit:
https://brainly.com/question/3493733
#SPJ1
tigate
b) The construction of a tangent to a circle given a point outside the circle can be justified using the
second corollary to the inscribed angle theorem. An alternative proof of this construction is shown
below. Complete the proof. (5 points)
Given: Circle C is constructed so that CD = DE = AD; CA is a radius of circle C.
Prove: AE is tangent to circle C.
1.
2.
3.
4.
5.
C
A
Statements
CD=DE
D
Circle C is constructed so that CD = DE = AD;
CA is a radius of circle C.
CD DE LAD
AACD is an isosceles triangle;
AADE is an isosceles triangle.
m/CAD+mzDCA+mzADC = 180º;
mzDAE+mzAED+mZEDA=
180°
E
1.
2.
3.
4.
Given
Reasons
Definition of congruence
Isosceles triangle
Substitution property
5. Isosceles triangle theorem
Answers
The proof that AE is tangent to circle C is given below:
What is the angle addition postulate?The angle addition postulate is a fundamental concept in geometry that states that the measure of an angle formed by two adjacent angles can be obtained by adding the measures of the two angles.
More specifically, given two adjacent angles with measures A and B, the measure of the angle formed by the two adjacent angles (denoted as AOB) can be found by adding the measures of the two angles:
A + B = AOB
This postulate is often used in geometric proofs and can be applied to any adjacent angles, including those formed by intersecting lines, parallel lines, or polygons.
Read more about angle addition postulate here:
https://brainly.com/question/24746945
#SPJ1
Explain what the constant of proportionality means in the equation 1 over 2 x + y
Answers
In the equation 1 over 2 x + y=c, the constant proportionality is defined as c. It displays the line's y-intercept and slope.
What is constant of proportionality?If the ratio of one statistic to the other is constant, then there is a proportional relationship between the two variables.
The ratio of y to x is the constant of proportionality if x and y have a proportional connection. At times, we can also say that x is to y.
The proportionality constant, or c, in the equation 1 over 2 x + y = c serves as a gauge for how quickly two variables change. The proportionality constant's value doesn't change when the value of one of the variables does.
A linear equation with two variables, x and y, is 1 over 2x + y = c. In the x-y plane, it symbolises a straight line.
If x = 0
Then,
1/2(0) + y = c
y = c
The proportionality constant, c, can be seen in the equation
1 over 2 x + y = c.
This number, which is unrelated to the actual values of the variables, shows the relationship between the two variables x and y.
The slope of the line connecting the two variables is another name for the constant of proportionality.
Two variables, x and y, are included in the equation 1 over 2 x + y = c in addition to the proportionality constant. The two quantities that
are being compared are represented by these variables.
In the equation 1 over 2 x + y=c, the proportionality constant is defined as c. It displays the line's y-intercept and slope.
To know more about constant proportionality, visit:
https://brainly.com/question/27598477
#SPJ1
The Complete questions as follows-
Explain what the constant of proportionality means in the equation 1 over 2 x + y = c
the tables show the cost of bagels at four different bakeries. choose two bakeries with the same unit cost.
Answers
Answer:The diagram shows the market demand and supply curves for the bread market. You know that there are 250 identical bakeries operating in the market
Step-by-step explanation:
An actuarial study finds that in a sample of 2000 18-year-old drivers, 124 are involved in an accident.
cost of such an accident to the insurance company is $15 000. If the company wants to make a 20% profit on policies, what should they charge 18-year-old drivers?
Answers
Answer: Let's start by calculating the probability that an 18-year-old driver is involved in an accident:
P(accident) = 124/2000 = 0.062
Let's assume that the insurance company pays the full cost of the accident, which is $15,000. Then the expected cost of covering one 18-year-old driver is:
Expected cost = P(accident) x Cost of accident = 0.062 x $15,000 = $930
If the insurance company wants to make a 20% profit on policies, they need to charge a premium that covers their expected cost plus their desired profit. The premium, denoted by P, can be calculated as follows:
P = (Expected cost + Desired profit) / (1 - Profit margin)
where Profit margin is the percentage of the premium that represents the profit. In this case, Profit margin is 20%, or 0.20.
Substituting the values we have calculated, we get:
P = ($930 + 0.20 x $930) / (1 - 0.20)
= $1,236.00
Therefore, the insurance company should charge 18-year-old drivers a premium of $1,236.00 to make a 20% profit on policies.
Step-by-step explanation:
Please help I’m confused
Answers
The value of c in cubic and quadratic function is -6
What is the value of cWhen x = -1, the equation of the line becomes:
y = 3(-1) + 4 = 1
We can substitute this value of y into the equation of the curve:
1 = -2(-1)³ - 3(-1)² + 8(-1) + c
Simplifying and solving for c, we get:
1 = 2 - 3 + 8 + c
c = -6
Therefore, the value of c is -6.
Learn more on equation of the curve here;
https://brainly.com/question/31132469
#SPJ1
In a 30°-60°-90° triangle, what is the length of the hypotenuse when the shorter leg is 5 cm?
Answers
Can you help me please
The half-life of Radium-226 is 1590 years. If a sample contains 300 mg, how many mg will remain after 2000 years? ---------
Answers
A = A₀ (1/2)^(t/T)
where A₀ is the initial amount, A is the final amount, t is the time elapsed, and T is the half-life. Substituting the given values, we get:
A = 300 (1/2)^(2000/1590) = 117.2 mg (rounded to one decimal place)
Therefore, approximately 117.2 mg of Radium-226 will remain after 2000 years.
can anyone explain how to solve this
Mortgage (monthly)
Amount
$985.64
Cell phone (monthly)
$58.30
Groceries (twice a month
$154.00
Clothing (monthly with 25% job-related) $180.00
Water & electric (monthly)
S128.40
Weekly dinner & movie
$55.00
Property taxes (6 months)
$684.80
Car insurance (guarterly)
$330.00
Your realized income is $2.943.20/month. How much are your fixed expenses each month? How much could you save per month if you take 25% of your discretionary monies and put it in a savings account?
Answers
Answer:
To calculate the fixed expenses each month, we need to add up all the monthly expenses:
Mortgage: $985.64
Cell phone: $58.30
Groceries: $154.00 x 2 = $308.00
Clothing (with 25% job-related): $180.00
Water & electric: $128.40
Weekly dinner & movie: $55.00 x 4 = $220.00
Total monthly fixed expenses: $1,880.34
To calculate how much could be saved per month, we need to first calculate the discretionary income:
Realized income: $2,943.20
Fixed expenses: $1,880.34
Discretionary income: $2,943.20 - $1,880.34 = $1,062.86
25% of discretionary income: 0.25 x $1,062.86 = $265.72
Therefore, the amount that could be saved per month by putting 25% of the discretionary income in a savings account is $265.72.
The distribution of scores on a standardized test is approximately normal with
a standard deviation of 40. Suppose a sample of 100 students had a mean
score of 180.23.
Find the margin of error for a 90% confidence interval for the mean score of all
students on this test. Round your answer to two decimal places.
Answers
Answer: The margin of error (ME) for a 90% confidence interval using a normal distribution with a known population standard deviation is given by:
ME = z* (σ/√n)
where z* is the z-score corresponding to the desired confidence level (in this case, 90% confidence), σ is the population standard deviation, and n is the sample size.
Using a z-score table or calculator, we find that the z-score corresponding to a 90% confidence level is 1.645.
Substituting the given values, we have:
ME = 1.645 * (40 / √100) = 6.58
Therefore, the margin of error for a 90% confidence interval for the mean score of all students on this test is 6.58. We can report the 90% confidence interval as:
180.23 ± 6.58 or (173.65, 186.81)
Step-by-step explanation:
Determine whether the following statements are TRUE or FALSE (do not write down the statements
just state TRUE or FALSE). [7 marks]
a. () ≥ 1 for any event .
b. () = 1 where is the Sample space.
c. If {} is any finite or infinite sequence of disjoint events, then (⋃
=1 ) = ∑ ()
=1 .
d. If ⊆ where and are two events in a sample space, then () ≤ ().
e. If and are two events in a sample space, then ( ∪ ) = () − () + ( ∩ ).
f. If and are two independent events in a sample space, then ( ⁄ ) = (∩)
() .
g. Mutually exclusive events are not independent
Answers
a. TRUE, b. TRUE, c. TRUE, d. TRUE, e. TRUE, f. FALSE, g. TRUE
How to determine whether the following statements are TRUE or FALSEa. TRUE: The probability of an event can never be negative, and can at most be equal to 1, which represents certainty.
b. TRUE: The sample space is the set of all possible outcomes of an experiment, and the probability of the sample space is always equal to 1, since one of the outcomes must occur.
c. TRUE: If the events in a sequence are disjoint, then they have no outcomes in common, so the probability of the union of the events is the sum of the probabilities of the individual events.
d. TRUE: If one event is a subset of another event, then the probability of the subset is less than or equal to the probability of the superset. This follows from the fact that the subset contains fewer outcomes than the superset.
e. TRUE: The probability of the union of two events is the probability of the first event plus the probability of the second event, minus the probability of the intersection of the events, which is the probability of both events occurring together. This is known as the inclusion-exclusion principle.
f. FALSE: The formula (P(A ∩ B) = P(A)P(B)) only applies to independent events, but not all independent events are mutually exclusive. For example, if A is the event of rolling a 4 on a die, and B is the event of rolling an even number, then A and B are independent, but not mutually exclusive.
g. TRUE: If two events are mutually exclusive, then they have no outcomes in common, so the occurrence of one event tells us that the other event cannot occur. This dependence means that the events are not independent.
Learn more about set theory at https://brainly.com/question/28916593
#SPJ1
Need help asap!!
Find the value of X
Answers
The answer is X + 5 = 10
X = 5
Use the box plot showing the ages of those who watch the television show 'The Code" to answer the question that follows.
Which value is the best approximation for the range in ages for the middle 50% of viewers?
A) 10
B) 15
C) 20
D) 45
Answers
The range in ages for the middle 50% of viewers is the interquartile range (IQR), which is the height of the box in the box plot. The best approximation is C) 20.
What is interqurtile range?The interquartile range (IQR) is a measure of statistical dispersion that represents the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of a dataset. It is a useful measure of spread because it is not influenced by outliers.
What is Range?Range is a statistical measure that represents the difference between the highest and lowest values in a set of data. It provides a simple indication of the spread or variability of the data.
According to the given information:
A box plot is a graphical representation of the distribution of a dataset. The box in the plot represents the middle 50% of the data, with the lower end of the box representing the 25th percentile (Q1) and the upper end of the box representing the 75th percentile (Q3). The distance between Q1 and Q3, which is represented by the height of the box, is called the interquartile range (IQR).
To answer the question, we need to find the best approximation for the range in ages for the middle 50% of viewers. From the box plot, we can see that the height of the box is approximately 20 units, which is the IQR. Therefore, the best approximation for the range in ages for the middle 50% of viewers is option C) 20. This means that 50% of viewers are between Q1-10 to Q3+10, where Q1 is the 25th percentile and Q3 is the 75th percentile.
To know more about interquartile range and range visit:
https://brainly.com/question/29204101
#SPJ1
Please answer all the steps and what the question states for each question in the image I need this and you’ll get 55 points and mark Brainiest!
Answers
1. The new volume will be 60 cubic feet. 2. Molly will earn $31.25 if she sells all of the dog beds after subtracting the cost of the fabric.
Describe Volume?In general, volume refers to the amount of space occupied by an object or substance, measured in three dimensions: length, width, and height. It is a physical quantity that is typically expressed in cubic units, such as cubic meters (m³), cubic centimeters (cm³), or cubic feet (ft³).
1. The volume of the cuboid is calculated as follows:
Volume = length x width x height
Volume = 5 ft x 3 ft x 2 ft
Volume = 30 cubic feet
If we double the height, the new height will be 2 x 2 ft = 4 ft. The new volume can be calculated as:
New Volume = length x width x new height
New Volume = 5 ft x 3 ft x 4 ft
New Volume = 60 cubic feet
Therefore, the new volume will be 60 cubic feet.
2. Step 1: Determine how many dog beds Molly can make with the fabric she bought.
Molly bought 12.5 yards of fabric, and she uses 2.5 yards of fabric for each dog bed. We can use division to find how many dog beds she can make:
12.5 yards / 2.5 yards per dog bed = 5 dog beds
Therefore, Molly can make 5 dog beds with the fabric she bought.
Step 2: Calculate the cost of the fabric for each dog bed.
Molly bought the fabric for $4.50 per yard, and she uses 2.5 yards of fabric for each dog bed. Therefore, the cost of the fabric for each dog bed is:
$4.50 per yard x 2.5 yards per dog bed = $11.25 per dog bed
Step 3: Calculate the revenue from selling one dog bed.
Molly sells each dog bed for $17.50.
Step 4: Calculate the profit from selling one dog bed.
Profit = revenue - cost
Profit = $17.50 - $11.25
Profit = $6.25
Step 5: Calculate the total revenue from selling all of the dog beds.
Molly can make 5 dog beds, and each dog bed sells for $17.50. Therefore, the total revenue is:
5 dog beds x $17.50 per dog bed = $87.50
Step 6: Calculate the total cost of the fabric for all of the dog beds.
Molly uses 2.5 yards of fabric for each dog bed, and she can make 5 dog beds. Therefore, the total cost of the fabric is:
2.5 yards per dog bed x 5 dog beds = 12.5 yards
$4.50 per yard x 12.5 yards = $56.25
Step 7: Calculate the total profit from selling all of the dog beds.
Profit = revenue - cost
Profit = $87.50 - $56.25
Profit = $31.25
Therefore, Molly will earn $31.25 if she sells all of the dog beds after subtracting the cost of the fabric.
To know more about profit visit:
https://brainly.com/question/19338486
#SPJ1
Solve on the interval [0,2pi):
1 - cos theta = 2-√3/2
Answers
Thus, the solution of the given cosine function is obtained for the angles- θ = 30º and θ = 330º between the intervals of [0,2pi).
Explain about the cosine function:The ratio of the triangle's side next to the angle to the hypotenuse is known as the cosine function. Thus, the cosine function does have a period of 2π, we can say.
Normally, radians rather than degrees are used when examining the cosine function in this manner. The common unit of measurement for angles in mathematics is the radian. 360° is equivalent to two radians, or one full circle.
Given data:
Function: 1 - cosθ = (2-√3)/2Interval - [0,2pi)1-cosθ = (2-√3)/2
cosθ = 1-(2-√3)/2
isolating the cosθ function:
cosθ = 1-(1-[√3/2])
cosθ = 1-1+√3/2
cosθ = √3/2
Now,
cos is √3/2 for ∏/6 = 30º and for 11∏/6 = 330º (Interval - [0,2pi))
Thus, the solution of the given cosine function is obtained for the angles-
θ = 30º and θ = 330º between the intervals of [0,2pi).
Know more about the cosine function
https://brainly.com/question/26993851
#SPJ1
If P = 3x² - x + 2 and Q = x² + 5x - 6, then P+ Q =
Answers
Answer:
Step-by-step explanation:
If P = 3x² - x + 2 and Q = x² + 5x - 6, then P+ Q = 3x² - x + 2 + x² + 5x - 6 =
4x^2 +4x - 4
D = 16 + 64 = 80
x12 = [tex]\frac{-4+-\sqrt{80} }{8}[/tex]
A hiker on the Appalachian Trail planned to increase the distance covered by 10% each day. After 7 days, the total distance traveled is 56.923 miles.
Part A: How many miles did the hiker travel on the first day? Round your answer to the nearest mile and show all necessary math work. (4 points)
Part B: What is the equation for Sn? Show all necessary math work. (3 points)
Part C: If this pattern continues, what is the total number of miles the hiker will travel in 14 days? Round your answer to the hundredths place and show all necessary math work. (3 points)
Answers
Let x be the distance traveled on the first day. Then, the distance traveled on the second day is 1.1x, on the third day is 1.1(1.1x) = 1.21x, and so on. After 7 days, the total distance traveled is:
x + 1.1x + 1.21x + ... + (1.1)^6 x = 56.923
Using the formula for the sum of a geometric series, we have:
x(1 - (1.1)^7)/(1 - 1.1) = 56.923
x(1 - 1.1^7)/(-0.1) = 56.923
x = 56.923(-0.1)/(1 - 1.1^7) ≈ 4 miles
Therefore, the hiker traveled approximately 4 miles on the first day.
The equation for Sn, the sum of the first n terms of the sequence, is:Sn = x(1 - r^n)/(1 - r)
where x is the first term, r is the common ratio (in this case, 1.1), and n is the number of terms.
Using the equation for Sn from Part B, we can find the total number of miles the hiker will travel in 14 days:S14 = x(1 - 1.1^14)/(1 - 1.1)
S14 ≈ 167.63
Therefore, the hiker will travel approximately 167.63 miles in 14 days.
More on geometric series can be found here: https://brainly.com/question/4617980
#SPJ1
5. A type of bacteria doubles in number every 25 minutes. Find the constant k
for this type of bacteria, then write the equation for modeling this exponential
growth.
Answers
To find the constant k for this type of bacteria, we can use the formula for exponential growth:
N(t) = N0 * e^(kt)
where N(t) is the number of bacteria at time t, N0 is the initial number of bacteria, e is Euler's number (approximately 2.71828), and k is the constant we're looking for.
We know that the bacteria doubles in number every 25 minutes, which means that after 25 minutes, the number of bacteria will be 2 times the initial number (N0). Therefore, we can write:
N(25) = 2 * N0
Substituting this into the formula, we get:
2 * N0 = N0 * e^(k*25)
Dividing both sides by N0 and simplifying, we get:
2 = e^(25k)
Taking the natural logarithm of both sides, we get:
ln(2) = 25k
Solving for k, we get:
k = ln(2)/25 ≈ 0.0278
Therefore, the equation for modeling the exponential growth of this type of bacteria is:
N(t) = N0 * e^(0.0278t)
*IG:whis.sama_ent
k = ln(2)/25
where ln(2) is the natural logarithm of 2.
To model the exponential growth of the bacteria population over time, we can use the equation:
N(t) = N0 * e^(kt)
where N(t) is the population size at time t, N0 is the initial population size, e is the mathematical constant approximately equal to 2.71828, k is the growth rate constant we just calculated, and t is the time elapsed.
So, if we start with an initial population of N0 bacteria, the population after time t can be calculated as:
N(t) = N0 * e^(kt)
I need help with this please
Answers
Answer:
thats 4th grade math... 0_0 but the answer is 414 ft².
Step-by-step explanation:
So you need to do 23x18 which equals 414. Listen to your teacher in class please kid. But you do you boo
Hiya, I need help on a few questions URGENTLY
Boris has a coin collection that contains US, Euro and British coins.If the ratio of US to Euro coins is 5 to 2 and the ratio of Euro to British coins is 5 to 1. What is the ratio of US to British coins?
Amanda works at the local cafe and gets paid £10 per hour (h) and a fixed sum of £50 for a month. Write a formula for the money (m) that she will receive in a month?
A holiday package costs £190, plus £50 a day. What. formula shows the cost of the holiday, C for d days?
Answers
The ratio of US to British coins is 25 to 4.
The second term, £50, is a fixed sum she receives regardless of the number of hours worked.
The first term, £190, represents the fixed cost of the holiday package. The second term, £50d, represents the additional cost per day, which is £50 multiplied by the number of days.
How to solve the Problem?1. The ratio of US to Euro coins is 5 to 2, and the ratio of Euro to British coins is 5 to 1. To find the ratio of US to British coins, we can combine these ratios.
First, we need to make sure that the ratios have a common term. We can do this by multiplying the first ratio (US to Euro) by 5, which gives us a ratio of 25 to 10.
Next, we can use the second ratio (Euro to British) to convert Euro coins to British coins. Since the ratio is 5 to 1, for every 5 Euro coins, there is 1 British coin. So for every 10 Euro coins, there are 2 British coins.
Finally, we can combine the US to Euro ratio (25 to 10) with the Euro to British ratio (10 to 2) to get the ratio of US to British coins.
25 : 10 :: 10 : 2
Multiplying both sides by 2, we get:
50 : 20 :: 10 : 2
Simplifying, we get:
The ratio of US to British coins is 25 to 4.
2. To calculate Amanda's monthly pay, we can use the formula:
m = 10h + 50
where m is the total money Amanda receives in a month, and h is the number of hours she works.
The first term, 10h, represents her pay for the number of hours she works, which is £10 per hour. The second term, £50, is a fixed sum she receives regardless of the number of hours worked.
3. To calculate the cost of the holiday package for d days, we can use the formula:
C = 190 + 50d
where C is the cost of the holiday package, and d is the number of days.
The first term, £190, represents the fixed cost of the holiday package. The second term, £50d, represents the additional cost per day, which is £50 multiplied by the number of days.
Learn more about fixed cost here: https://brainly.com/question/30641520
#SPJ1
In a lab experiment, the decay of a radioactive isotope is being observed. At the
beginning of the first day of the experiment the mass of the substance was 1500
grams and mass was decreasing by 10% per day. Determine the mass of the
radioactive sample at the beginning of the 10th day of the experiment. Round to the
nearest tenth (if necessary).
Answers
The radioactive isotope has a final mass of 523 grams.
How to predict the mass of a radioactive isotope in time
Herein we find the case of a radioactive isotope, whose mass is decreasing exponentially in time. Whose expression is described below:
m(x) = a · (1 - r / 100)ˣ
Where:
a - Initial mass of the radioactive isotope, in grams.r - Decrease rate, in percentage.x - Time, in daysIf we know that a = 1500, r = 10 and x = 10, then the mass of the radioactive isotope is:
m(10) = 1500 · 0.90¹⁰
m(10) = 523.018
The final mass of the radioactive isotope is equal to 523 grams.
To learn more on exponential decay: https://brainly.com/question/14355665
#SPJ1
please help me fill these boxes
Answers
The measurements for area of Jacobs yard are;
Part A = 6m x 3m = 18m
Part B = 4.5m x 3m = 13 m
Part C = 1/2 x 3m x 3m = 4.5 m²
Total area = 18m² + 13.5m² + 4.5m² = 36m²
How do you identify sections that would help in calculating area?To identify sections that would help in calculating area, you need to look for shapes or figures that can be divided into simpler geometric shapes, such as squares, rectangles, triangles, and circles.
Once you have identified the simpler shapes, you can use their formulas to calculate their areas and then add them together to find the total area of the larger shape or figure.
For example, a rectangle can be divided into two triangles or two smaller rectangles, and a circle can be divided into a sector or a ring. Breaking down a larger shape into smaller, simpler shapes can make it easier to calculate their areas accurately.
Jacob is putting tiles on the section of his yard labeled A, B, C. What is the area of the parts that need tiles?
Part A = .............. x ........... = ...........m
Part B = + .............. x ............. = ............ m
Part C = 1/2 x ................. x ............ = ............... m²
Total area = ................... + ..................... + .................. = ..............m
Find more exercises on calculating area;
https://brainly.com/question/30656333
#SPJ1
The law of
applies during online sales
of shoes that is when consumers rush to buy products at 50% discounts.
The law of
Answers
The law of demand applies during online sales of shoes; that is when consumers rush to buy products at 50% discount.
What is the law of demand?In Mathematics and Economics, the law of demand can be defined as an economic theory which states that there exist a negative relationship between the price of a product (good) and the quantity of the product (good) that is being demanded by consumers.
This ultimately implies that, holding all the other factors constant, there would be a significant decrease (fall or decline) in the demand for a product (good) and service when the price of a product (good) and service in the market increases (rises), and vice-versa in accordance with the law of demand.
Read more on the law of demand here: brainly.com/question/24500422
#SPJ1
Complete Question:
The law of ___________applies during online sales of shoes; that is when consumers rush to buy products at 50% discount
Find the area of the trapezoid 11 yd 11 yd 7 yd
Answers
Answer:
Step-by-step explanation:
A=1/2(b1+b2)h
=1/2 (11yd+11yd)(7yd)
=1/2(22yd)(7yd)
=(11yd)(7yd)
=77yd
1/2x + 2y, when x = 7 and y=8 help me please
Answers
Answer:
39/2 or 19.5
Step-by-step explanation:
To evaluate the expression 1/2x + 2y when x = 7 and y = 8, we can substitute the values of x and y into the expression and perform the necessary calculations.
Given:
x = 7
y = 8
Plugging these values into the expression, we get:
1/2(7) + 2(8)
Now, we can follow the order of operations (PEMDAS/BODMAS) to simplify the expression:
1/2(7) + 2(8)
= 1/2 * 7 + 2 * 8 (Multiplication has higher precedence than addition)
= 7/2 + 16 (Performing the multiplications)
= 7/2 + 32/2 (Finding the common denominator for addition)
= (7 + 32)/2 (Adding the numerators)
= 39/2 (Simplifying the fraction)
So, the value of the expression 1/2x + 2y when x = 7 and y = 8 is 39/2 or 19.5.
Help please i need this asap!! I'll give 100 points
Answers
The range is expressed in interval notation as (-1, ∞)
How to find the function (f+g)(x)?To find the linear function f(x), let us use the table given.
A linear function with the following equation that passes through the points (a, g(a)) and (b, g(b)):
[tex]g(x) - g(a) = \frac{g(b)-g(a)}{b-a} (x-a)[/tex]
Because the g(x) line crosses through points (-6, 14) and (-3, 8), we have:
a = -6, g(a) = 16, b = -3 and, g(b) = 10
Therefore g(x)
[tex]g(x) - (16) = \frac{10-16}{-3-(-6)} (x--(6))\\g(x) - 16 = \frac{10-16}{-3+6} (x+6)\\g(x) - 16 = \frac{-6}{3} (x+6)\\g(x) - 16 = -2(x +6)\\g(x) = -2x -12+16\\g(x) = -2x+4[/tex]
now find the (f+g)(x).
[tex](f+g)(x) = f(x) + g(x) = x^{2} + 2x -5 -2x + 4\\(f+g)(x) = f(x) + g(x) = x^{2} - 1\\[/tex]
(f+g)(x) = (x-1)(x+1), therefore we get the values x = 1 and x = -1
The parabola's vertice has x-coordinate 0 (the midway between the roots). At x = 0, we get:
[tex](f +g)(x) = 0^{2} - 1 = -1[/tex]
Furthermore, because the coefficient of [tex]x^{2}[/tex] is 1, which is positive, this function indicates a parabola that has been opened upwards.
As a result, the function's minimal value is y = -1. As a result, the function's range includes all real numbers equal to or greater than -1.
The range is expressed in interval notation as (-1, ∞)
Learn more about function here:
https://brainly.com/question/12431044
#SPJ1
Use the graph to answer the questions
WILL MARK BRAINLIEST!!
Answers
The diagram of the Gateway Arch on the coordinate plane, analyzed using quadratic equations indicates;
1. The vertex point is (50, 630)
2. The solution point are; (20, 0), and (80, 0)
3. Vertex form; f(x) = -0.7·(x - 50)² + 630
4. Factored form; f(x) = -0.7·(x - 20)·(x - 80)
What is a quadratic equation?A quadratic equation is an equation of the form f(x) = a·x² + b·x + c
1. The vertex obtained from the graphical diagram of the Gateway Arch indicates that the point corresponding to the vertex point is; (50, 9 × 70 = 630)
The vertex point is; (50, 630)
2. The solution are the points the curve of the Gateway intersects the x-axis, which are points where the y-axis values are zero, therefore;
The solutions are; (20, 0), and (80, 0)
3. The vertex form of a quadratic equation is; f(x) = a·(x - h)² + k
Where;
(h, k) = The coordinates of the vertex
Therefore;
(h, k) = (50, 630)
f(20) = 0 = a·(20 - 50)² + 630
a·(20 - 50)² = -630
a = -630/((20 - 50)²) = -630/900 = -7/10
a = -7/10 = -0.7
The vertex form quadratic equation is therefore; f(x) = -0.7·(x - 50)² + 630
4. The factored form of a quadratic equation is; f(x) = a·(x - r₁)·(x - r₂)
r₁ = 20, and r₂ = 80, a obtained from the vertex is; a = -0.7
The factored form is therefore; f(x) = -0.7·(x - 20)·(x - 80)
Learn more on the factored form of a quadratic equation here: https://brainly.com/question/25094938
#SPJ1
Work out sheet below please
Answers
Answer:
-4 + 8 = 4
-2 + 6 = 4
-1 + 5 = 4
So the three pairs are -4 and 8; -2 and 6; and -1 and 5.
Find any solution(s) (refer to attachment) of and select the correct statement.
A. The equation has no solution.
B. The equation has two solutions.
C. The equation has one solution.
D. The equation has one solution and one extraneous solution.
Answers
x+2=0
x-1=0
x≠-1
x1=-2, x2=1
Find the slope of the line tangent to the graph of the function at the given value of x.
y = x4 + 2x3 + 2x + 2 at x = -3
Answers
Answer:
To find the slope of the line tangent to the graph of the function at x = -3, we need to find the derivative of the function and evaluate it at x = -3.
First, let's find the derivative of the function y = x^4 + 2x^3 + 2x + 2:
y' = 4x^3 + 6x^2 + 2
Now, let's evaluate y' at x = -3:
y'(-3) = 4(-3)^3 + 6(-3)^2 + 2
= -108 + 54 + 2
= -52
Therefore, the slope of the line tangent to the graph of the function y = x^4 + 2x^3 + 2x + 2 at x = -3 is -52.