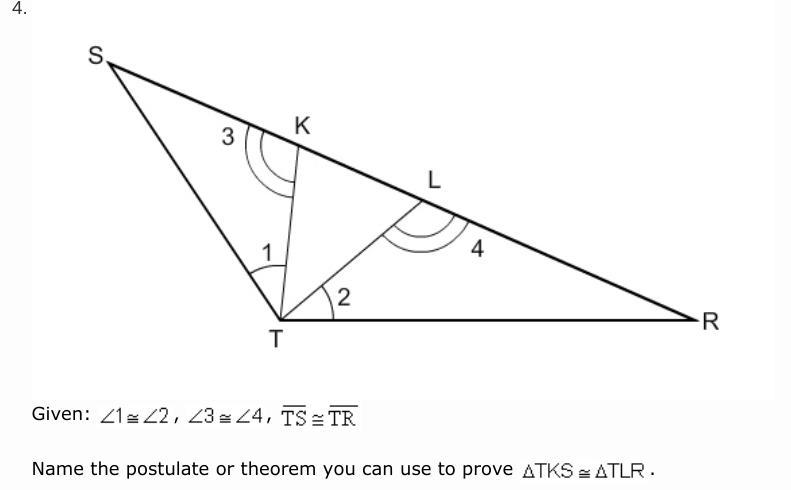
Given: (in picture as I cannot type it like that.) Name the postulate or theorem you can use to prove: (also in the picture) A. HL Theorem B. AAS Theorem C. SAS Postulate D. ASA Postulate

Answer:

36 tickets

Step-by-step explanation:

At a city museum, child tickets are sold for $5.30, and adult tickets are sold for $9.40

The total sales that were made are $1206

Let x represent the number of child tickets that were sold

Let y represent the number of adult tickets that was sold

5.30x +9.40y= 1206

The number of adult tickets sold was three times greater than the child tickets

y= 3x

Substitute 3x for y in the equation

5.30x + 9.40y= 1206

5.30x + 9.40(3x)= 1206

5.30x + 28.2x= 1206

33.5x= 1206

Divide both sides by the coefficient of x which is 33.5

33.5x/33.5= 1206/33.5

x = 36

Hence the number of child tickets that were sold that day is 36 tickets

Answer:

[tex]\boxed{V=lwh}[/tex]

Step-by-step explanation:

The formula for volume of a cuboid is:

[tex]V=lwh[/tex]

[tex]volume = length \times width \times height[/tex]

Answer:

V = l w h

Step-by-step explanation:

Volume of a Cuboid = Length × Width × Height

Where l = length, w = width and h = height

Answer:

The correct answer is

For addition, Caulleen used the words total, sum, altogether, and increase. But we could also have used the words combine, plus, more than, or even just the word "and". For subtraction, Caulleen used the words, fewer than, decrease, take away, and subtract. We also could have used less than, minus, and difference.

Step-by-step explanation:

hope this helps u!!!

Answer:

Step-by-step explanation:

[tex]f(x) = 4 {e}^{x} [/tex]

[tex]f(2) = 4 {e}^{2} [/tex]

[tex]f(2) = 4 \times 7.389[/tex]

[tex]f(2) = 29.6[/tex]

( Approximately 30)

Hope this helps..

Good luck on your assignment..

Answer:

approximately 30

Step-by-step explanation:

[tex]f(x)=4e^x[/tex]

Put x as 2 and evaluate.

[tex]f(2)=4e^2[/tex]

[tex]f(2)=4(2.718282)^2[/tex]

[tex]f(2)= 29.556224 \approx 30[/tex]

Answer:

x < -( 8-2b) /a  a > 0

Step-by-step explanation:

−ax + 2b > 8

Subtract 2b from each side

−ax + 2b-2b > 8-2b

-ax > 8 -2b

Divide each side by -a, remembering to flip the inequality ( assuming a>0)

-ax/-a < ( 8-2b) /-a

x < -( 8-2b) /a  a > 0

Answer: [tex]x<\frac{-8+2b}{a}[/tex]

                  [tex]a>0[/tex]

Step-by-step explanation:

[tex]-ax+2b>8[/tex]

[tex]\mathrm{Subtract\:}2b\mathrm{\:from\:both\:sides}[/tex]

[tex]-ax>8-2b[/tex]

[tex]\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}[/tex]

[tex]\left(-ax\right)\left(-1\right)<8\left(-1\right)-2b\left(-1\right)[/tex]

[tex]ax<-8+2b[/tex]

[tex]\mathrm{Divide\:both\:sides\:by\:}a[/tex]

[tex]\frac{ax}{a}<-\frac{8}{a}+\frac{2b}{a};\quad \:a>0[/tex]

[tex]x<\frac{-8+2b}{a};\quad \:a>0[/tex]

Answer:

(3) x ≥ -3

(4) 2.5 gallons

(4) -12x + 36

Step-by-step explanation:

Hey there!

1)

Well its a solid dot meaning it will be equal to.

So we can cross out 1 and 2.

And it's going to the right meaning x is greater than or equal to -3.

(3) x ≥ -3

2)

Well if each milk container has 1 quart then there is 10 quarts.

And there is 4 quarts in a gallon, meaning there is 2.5 gallons of milk.

(4) 2.5 gallons

4)

16 - 4(3x - 5)

16 - 12x + 20

-12x + 36

(4) -12x + 36

Hope this helps :)

Answer:

-3

Step-by-step explanation:

2x + 3 +7x = -24

Add the X together

9x +3 = -24

Bring over the +3. [when you bring over change the sign]

9x = -24 -3

9x = -27

-27 divide by 9 to find X

therefore answer is

x= -3.

Hope this helps

Answer:

x = -3

Step-by-step explanation:

question is

2x + 3 + 7x = -24

First you combine the like terms

2x and 7x you can add them so it will be 9x

so it will then it will be like this:

9x + 3 = -24

now you take the 3 and send it to the other side, and right now the 3 is positive so when it goes to the other side it will turn into -3

so

9x = -24 -3

again now you combine the like terms

-24 -3 = - 27

now you have

9x = -27

now just divide each side by 9

x = -27/9

x = -3

Sorry if this doesnt help

Answer:

[tex]79591.8872 in^3/s[/tex]

Step-by-step explanation:

we know that the volume of a right circular cone is give as

[tex]V(r,h)= \frac{1}{3} \pi r^2h\\\\[/tex]

Therefore differentiating partially  with respect to  r and h we have

[tex]\frac{dV}{dt} = \frac{1}{3}\pi [2rh\frac{dr}{dt} +r^2\frac{dh}{dt}][/tex]

[tex]\frac{dV}{dt} = \frac{\pi}{3} [218*198*1.1+109^2*2.4][/tex]

[tex]\frac{dV}{dt} = \frac{\pi}{3} [47480.4+28514.4]\\\\\frac{dV}{dt} = \frac{\pi}{3} [75994.8]\\\\ \frac{dV}{dt} = 3.142 [25331.6]\\\\ \frac{dV}{dt} =79591.8872 in^3/s[/tex]

Answer:

Step-by-step explanation:

Given that:

If C(x) =  the cost of producing x units of a commodity

Then;

then the average cost per unit is c(x)  = [tex]\dfrac{C(x)}{x}[/tex]

We are to consider a given function:

[tex]C(x) = 54,000 + 130x + 4x^{3/2}[/tex]

And the objectives are to determine the following:

a) the total cost at a production level of 1000 units.

So;

If C(1000) = the cost of producing 1000 units of a commodity

[tex]C(1000) = 54,000 + 130(1000) + 4(1000)^{3/2}[/tex]

[tex]C(1000) = 54,000 + 130000 + 4( \sqrt[2]{1000^3} )[/tex]

[tex]C(1000) = 54,000 + 130000 + 4(31622.7766)[/tex]

[tex]C(1000) = 54,000 + 130000 + 126491.1064[/tex]

[tex]C(1000) = $310491.1064[/tex]

[tex]\mathbf{C(1000) \approx $310491.11 }[/tex]

(b) Find the average cost at a production level of 1000 units.

Recall that :

the average cost per unit is c(x)  = [tex]\dfrac{C(x)}{x}[/tex]

SO;

[tex]c(x) =\dfrac{(54,000 + 130x + 4x^{3/2})}{x}[/tex]

Using the law of indices

[tex]c(x) =\dfrac{54000}{x} + 130 + 4x^{1/2}[/tex]

[tex]c(1000) = \dfrac{54000}{1000}+ 130 + {4(1000)^{1/2}}[/tex]

c(1000) =$ 310.49 per unit

(c) Find the marginal cost at a production level of 1000 units.

The marginal cost  is C'(x)

Differentiating  C(x) = 54,000 + 130x + 4x^{3/2} to get  C'(x) ; we Have:

[tex]C'(x) = 0 + 130 + 4 \times \dfrac{3}{2} \ x^{\dfrac{3}{2}-1}[/tex]

[tex]C'(x) = 0 + 130 + 2 \times \ {3} \ x^{\frac{1}{2}}[/tex]

[tex]C'(x) = 0 + 130 + \ {6}\ x^{\frac{1}{2}}[/tex]

[tex]C'(1000) = 0 + 130 + \ {6} \ (1000)^{\frac{1}{2}}[/tex]

[tex]C'(1000) = 319.7366596[/tex]

[tex]\mathbf{C'(1000) = \$319.74 \ per \ unit}[/tex]

(d)  Find the production level that will minimize the average cost.

the average cost per unit is c(x)  = [tex]\dfrac{C(x)}{x}[/tex]

[tex]c(x) =\dfrac{54000}{x} + 130 + 4x^{1/2}[/tex]

the production level that will minimize the average cost is c'(x)

differentiating [tex]c(x) =\dfrac{54000}{x} + 130 + 4x^{1/2}[/tex] to get c'(x); we have

[tex]c'(x)= \dfrac{54000}{x^2} + 0+ \dfrac{4}{2 \sqrt{x} }[/tex]

[tex]c'(x)= \dfrac{54000}{x^2} + 0+ \dfrac{2}{ \sqrt{x} }[/tex]

Also

[tex]c''(x)= \dfrac{108000}{x^3} -x^{-3/2}[/tex]

[tex]c'(x)= \dfrac{54000}{x^2} + \dfrac{4}{2 \sqrt{x} } = 0[/tex]

[tex]x^2 = 27000\sqrt{x}[/tex]

[tex]\sqrt{x} (x^{3/2} - 27000) =0[/tex]

x= 0;  or  [tex]x= (27000)^{2/3}[/tex] = [tex]\sqrt[3]{27000^2}[/tex] = 30² = 900

Since  production cost can never be zero; then the production cost = 900 units

(e) What is the minimum average cost?

the minimum average cost of c(900) is

[tex]c(900) =\dfrac{54000}{900} + 130 + 4(900)^{1/2}[/tex]

c(900) = 60 + 130 + 4(30)

c(900) = 60 +130 + 120

c(900) = $310 per unit

Answer:

4 boys

Step-by-step explanation:

Let x represent boys and y represent girls

Hence, x : y = 3 : 2

x/y = 3/2  

2x = 3y ------ (1)

x/y + 4 = 3/3

3x = 3(y + 4)

3x = 3y + 12 --------- (2)

From (1): x = 3y/2

Substitute x into (2) we have:

9y/2 = 3y + 12

9y = 6y + 24

9y - 6y = 24

3y = 24

∴ y = 8

From (2) : 3x = 24 - 12 = 12

∴ x = 4

Hence there Four boys

The graph which shows the solution to the system of inequalities is attached in the picture below :

Given the inequalities :

y ≥ 2x + 1

y ≤ 2x - 2

From y ≥ 2x + 1 ;

Since the inequality sign is ≥, a solid line is used to draw the straight line graph of  y ≥ 2x + 1

From :

y = mx + c

Where, m = slope ; c = intercept

Hence, a straight line graph with ;

Intercept, c = 1 (where the line crosses the y-intercept)

Slope, m = 2

Consider a point, which isn't on the line ;

Take point (0,0) and use it to test the inequality :

0 ≥ 2(0) + 1

0 ≥ 0 + 1

0 ≥ 1

This is false, hence, the portion of the graph which does not contain (0, 0) is shaded.

From : y ≤ 2x - 2

Since the inequality sign is ≤, a solid line is used to draw the straight line graph of  y ≤ 2x - 2

Graph the line y ≤ 2x - 2, with ;

Intercept, c = - 2

Slope = 2

Consider a point, which isn't on the line ;

Take point (0,0) and use it to test the inequality y ≤ 2x - 2:

0 ≤ 2(0) - 2

0 ≤ 0 - 2

0 ≤ - 2

This is false, hence, the portion of the graph which does not contain (0, 0) is shaded.

Learn more : https://brainly.com/question/19670553

Answer:

Its graph B on edge 2022

Step-by-step explanation:

Answer:

To find the x-intercept, simply plug in the value y = 0 into your equation and then solve for x. To find the y-intercept, plug in x = 0 and solve for y.

Answer:

-1/2

Step-by-step explanation:

At this point you can guess and try. And it seems that x = -1/2, lets check:

So, this is correct: x= -1/2

Answer:

[tex]\large \boxed{\sf \ \ \dfrac{1}{x^2}+\dfrac{1}{x^2+x}=\dfrac{2x+1}{x^2(x+1)} \ \ }[/tex]

Step-by-step explanation:

Hello,

This is the same method as computing for instance:

[tex]\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{3+2}{2*3}=\dfrac{5}{6}[/tex]

We need to find the same denominator.

Let's do it !

For any x real different from 0, we can write:

[tex]\dfrac{1}{x^2}+\dfrac{1}{x^2+x}=\dfrac{1}{x^2}+\dfrac{1}{x(x+1)}\\\\=\dfrac{x+1+x}{x^2(x+1)}=\dfrac{2x+1}{x^2(x+1)}[/tex]

Hope this helps.

Do not hesitate if you need further explanation.

Thank you

Answer: 54 mL

Step-by-step explanation:

Simply do 9(number of containers)*6(Syrup per container) to get 54 mL of syrup.

Hope it helps <3

Answer: n = 2401

Step-by-step explanation:

Given;

Confidence level = 2% - 99%

n = ? ( which is the sample size is unknown ).

Solution:

Where;

n = [z/E]^2*pq

Since no known value for ( p ) estimate is given, the "least biased" estimate is p = 1/2

Substituting the given data into the formula.

n = [1.96/0.02]^2(1/2)(1/2)

n = 2401

The minimum number of truck drivers the statistician needs to sample for an accurate result is 2401

Answer:

Step-by-step explanation:

you have to keep going cause if you count the fives there's a 25 but right next to the 25 there's 24 all you have to do is watch what your doing just watch your steps

Answer:

70

Step-by-step explanation:

You have to find the vertical of x. To the right of the vertical, we see that there is an angle of 25 (since the 25 up top corresponds to that blank angle). Once you add 25 + 85 + x = 180 (since this is a straight line), we see that x is 70, and its vertical is also 70.

Answer:

36

Step-by-step explanation:

You did not attach a picture, so I just assumed where the lengths of 15 and 39 were.

Answer:

  181.8 yd

Step-by-step explanation:

The law of cosines is good for this. It tells you for triangle sides 'a' and 'b' and included angle C, the length of 'c' is given by ...

  c^2 = a^2 +b^2 -2ab·cos(C)

For the given geometry, this is ...

  c^2 = 400^2 +240^2 -2(400)(240)cos(16°) ≈ 33,037.75

  c ≈ √33037.75 ≈ 181.8 . . . yards

Marsha's ball is about 181.8 yards from the hole.

Answer:

181.8 yds

Step-by-step explanation:

I got it correct on founders edtell

When the wavelength of a diffraction grating is decreased,  the distance between lines decreases.

The diffraction grating is used to carry out interference experiments. It consists of a  number of small lines that are constructed to be close to each other and produce an interference pattern.

The outcome of decreasing the wavelength of incident light on a diffraction grating is that the distance between lines decreases.

Learn more about diffraction grating:https://brainly.com/question/13902808

#SPJ1

Answer:

8 and 9

Step-by-step explanation:

If x is the smaller integer, and x + 1 is the larger integer, then:

(x + 1)² + 3x = 105

x² + 2x + 1 + 3x = 105

x² + 5x − 104 = 0

(x + 13) (x − 8) = 0

x = -13 or 8

Since x is positive, x = 8.  So the two integers are 8 and 9.

Hey there! I'm happy to help!

We want to find the volume of this  rectangular waterbed. This means the amount of space it takes up. To find the volume of a rectangular prism, you just multiply together the three side lengths.

7×5×1=35 cubic feet

Now, we need to see how many gallons fit into 35 cubic feet. We see that one gallon is equal to 0.13 cubic feet. So, we can set up a proportion to find how many gallons are needed. We will use g to represent our missing number of gallons.

[tex]\frac{gallons}{cubic feet} = \frac{1}{0.13} =\frac{g}{35}[/tex]

In a proportion, the products of the diagonal numbers are equal. This means that 35, which is 1 multiplied by 35, is equal to 0.13g, which is from multiplying 0.13 by the g.

0.13g=35

We divide both sides by 0.13/

g≈269.23

When rounded to the nearest whole gallon, we will need 269 gallons of water to fill the waterbed.

I hope that this helps! Have a wonderful day! :D

Answer:

Step-by-step explanation:

Since the waterbed is rectangular, its volume would be determined by applying the formula for determining the volume of a cuboid which is expressed as

Volume = length × width × height

Therefore,

Volume of waterbed = 7 × 5 × 1 = 35 cubic feet

1 US gallon = 0.133680556 cubic feet

Therefore, converting 35cubic feet to gallons, it becomes

35/0.133680556 = 261.81818094772 gallons

Rounding up to whole gallon, it becomes 262 gallons

Answer:

Option (D)

Step-by-step explanation:

In the picture attached,

An obtuse angle triangle ABC has been given.

By applying Sine rule in the triangle,

[tex]\frac{\text{SinB}}{b}=\frac{\text{SinA}}{a}=\frac{\text{SinC}}{c}[/tex]

Since, m∠A + m∠B + m∠C = 180°

45° + 110° + m∠C = 180°

m∠C = 180°- 155° = 25°

[tex]\frac{\text{Sin110}}{b}=\frac{\text{Sin45}}{a}=\frac{\text{Sin25}}{7}[/tex]

[tex]\frac{\text{Sin110}}{b}=\frac{\text{Sin45}}{a}=0.060374[/tex]

[tex]\frac{\text{Sin110}}{b}=0.060374[/tex]

b = [tex]\frac{\text{Sin110}}{0.060374}[/tex]

b = 15.56

b ≈ 15.56

[tex]\frac{\text{Sin45}}{a}=0.060374[/tex]

a = [tex]\frac{\text{Sin45}}{0.060374}[/tex]

a = 11.712

a = 11.71

Therefore, Option (D) will be the answer.

Answer:

0.078

Step-by-step explanation:

The probability P(A) of an event A happening is given by;

P(A) = [tex]\frac{number-of-possible-outcomes-of-event-A}{total-number-of-sample-space}[/tex]

From the question;

There are two events;

(i) Drawing a first card which is a king: Let the event be X. The probability is given by;

P(X) = [tex]\frac{number-of-possible-outcomes-of-event-X}{total-number-of-sample-space}[/tex]

Since there are 4 king cards in the pack, the number of possible outcomes of event X = 4.

Also, the total number of sample space = 52, since there are 52 cards in total.

P(X) = [tex]\frac{4}{52}[/tex] = [tex]\frac{1}{13}[/tex]

(ii) Drawing a second card which is a queen: Let the event be Y. The probability is given by;

P(Y) = [tex]\frac{number-of-possible-outcomes-of-event-Y}{total-number-of-sample-space}[/tex]

Since there are 4 queen cards in the pack, the number of possible outcomes of event Y = 4

But then, the total number of sample = 51, since there 52 cards in total and a king card has been removed without replacement.

P(Y) = [tex]\frac{4}{51}[/tex]

Therefore, the probability of selecting a first card as king and a second card as queen is;

P(X and Y) = P(X) x P(Y)

= [tex]\frac{1}{13} * \frac{4}{51}[/tex] = 0.078

Therefore the probability is 0.078

Answer:

it took 7 hours for the bread to drop at a constent rate

Step-by-step explanation:

Answer:

3/11

Step-by-step explanation:

There are eleven equal parts.

So the denominator is 11.

He copies 8 parts on Sunday.

11-8=3.

He copied 3 parts on Saturday.

Hope this helps ;) ❤❤❤

Answer:

False

Step-by-step explanation:

To find <A, we can do 5x - 80 = 3x + 20.

As we simplify, we will get 2x = 100, which is x = 50

Therefore, <A will be 50 degrees and not 45 degrees.

Also, if you need y, you can do:

3y - 7 = y + 7

2y = 14

y = 7

Answer: A, (0, -3)

Step-by-step explanation:

Inequalities, once graphed, take the form of the image you attached:

Linear inequalities are straight lines, sometimes dotted and sometimes solid, with shading on one side of the line.

Any point in the shading is a correct solution to the inequality.

In this case, the line is solid, so any point on the line is a solution to the inequality.

Looking at answer choice A: (0, -3), it lies on the line as the y-intercept.

The correct choice is A.