Answers
Answer:
13. True, False, True
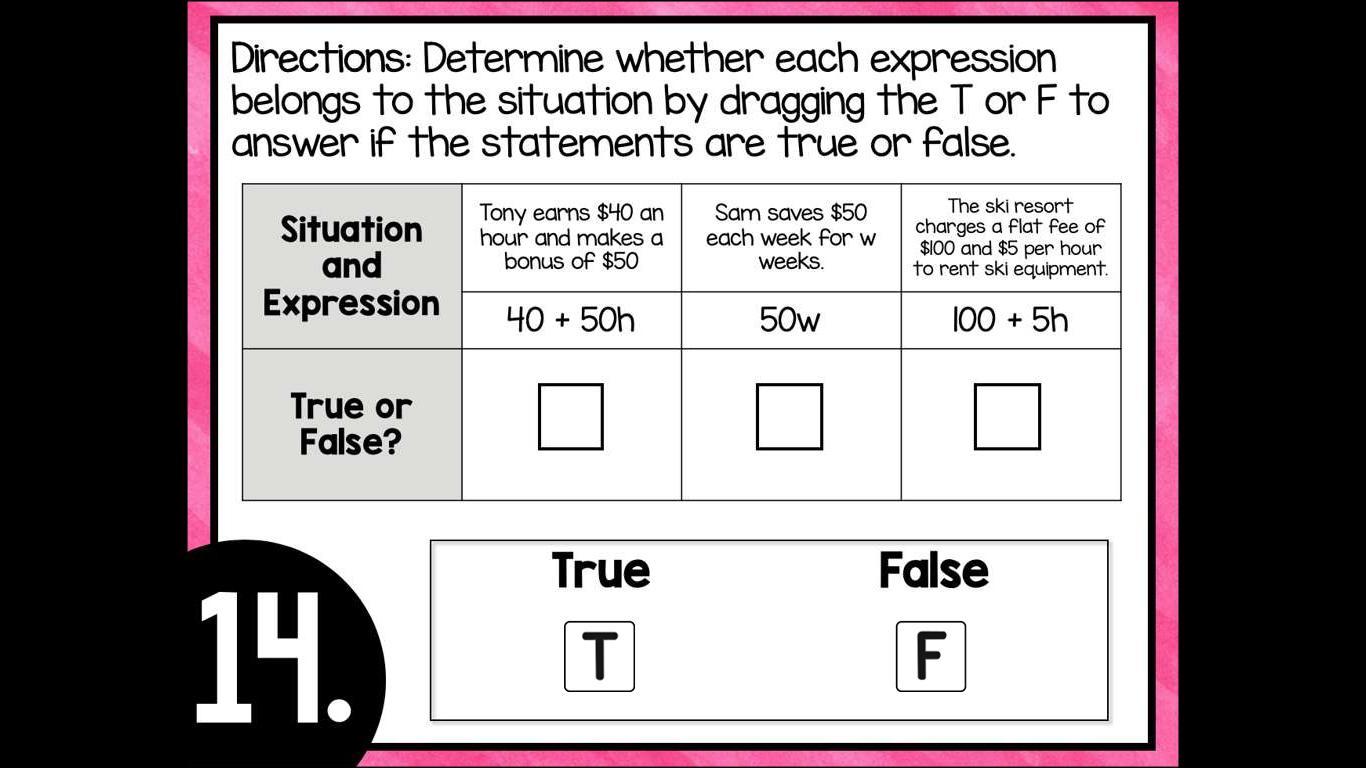
14. False, True, True
15. All true
Related Questions
Evaluate the triple integral. X dv, where e is bounded by the paraboloid x = 4y2 4z2 and the plane x = 4. E
Answers
The triple integral that is bounded by a paraboloid x = 4y2 4z2 given as 16.762
Parabloid, x = 4y² + 4z²
plane x = 4
x = 4y² + 4z²
x = 4
4 = 4y² + 4z²
4 = 4 (y² + z² )
1 = y² + z²
from polar coordinates
y = r cos θ
z = r sin θ
r² = y² + z²
The limits of the integral0 ≤ θ ≤ 2π
4r² ≤ x ≤ 4
0 ≤ r ≤ 1
[tex]\int\limits\int\limits\int\limits {x} \, dV = \int\limits^1_0\int\limits^a_b\int\limits^c_d {x} \, dx ( rdrdz)[/tex]
where
a = 4
b = 4r²
c = 2r
d = 0
The first integral using limits c and d gives:
[tex]2pi\int\limits^1_0\int\limits^a_b {xr} \, dx[/tex]
The second integral using limits a and b
[tex]pi\int\limits^1_0 {16 } } \, rdr - pi\int\limits^1_0 {16r^{5} \, dx[/tex]
[tex]16pi\int\limits^1_0 { } } \, rdr - 16pi\int\limits^1_0 {r^{5} \, dx[/tex]
[tex]16pi\int\limits^1_0 { } } \, [r-r^{5}]dr[/tex]
The third integral using limits 1 and 0 gives: 16.762
Read more on Triple integral here: https://brainly.com/question/27171802
The triple integral that is bounded by a paraboloid x = 4y2 4z2 given as 16.762
What is integration?Integration is defined as adding small parts to form a new significant part.
Parabloid, x = 4y² + 4z²
plane x = 4
x = 4y² + 4z²
x = 4
4 = 4y² + 4z²
4 = 4 (y² + z² )
1 = y² + z²
from polar coordinates
y = r cos θ
z = r sin θ
r² = y² + z²
The limits of the integral
0 ≤ θ ≤ 2π
4r² ≤ x ≤ 4
0 ≤ r ≤ 1
[tex]\int\int\intxdV = \int_0_1\int_b_a\int_d_cxdx(rdrdz)[/tex]
where
a = 4
b = 4r²
c = 2r
d = 0
The first integral using limits c and d gives:
[tex]2\pi\int_0^1\int_b^axydx[/tex]
The second integral using limits a and b
[tex]\pi \int_0^116rdr-\pi\int_0^116r^5dx[/tex]
[tex]16\pi \int_0^1rdr-16\pi\int_0^1 r^5dx[/tex]
[tex]16\pi\int_0^1[r-r^5]dr[/tex]
The third integral using limits 1 and 0 gives: 16.762
Read more on Triple integral here:
brainly.com/question/27171802
#SPJ4
A cyclist travels a distance of 837 1/2 feet in 25 seconds. The cyclist travels at a constant rate. What is the unit rate, in feet per second, at which the cyclist travels?
PLEASE
Answers
Answer:
[tex]\boxed{33.5 \ \text{feet/second}}[/tex]
Step-by-step explanation:
To find the unit rate, we need to find out how much distance does the cyclist travel in 1 second. For that, we need to use the unitary method. A unitary method is a method that determines the unit rate of an object.
Note: Since the cyclist travels at a constant rate, unitary method can be used.
[tex]\rightarrow 837 \dfrac{1}{2} \ \text{feet in 25 seconds}[/tex]
[tex]\rightarrow 837.5 \ \text{feet} = 25 \ \text{seconds}[/tex]
Divide both sides by 25:
[tex]\rightarrow \dfrac{837.5}{25} \ \text{feet} = \dfrac{25}{25} \ \text{seconds}[/tex]
[tex]\rightarrow 33.5 \ \text{feet} = 1 \ \text{seconds}[/tex]
[tex]\rightarrow \boxed{33.5 \ \text{feet/second}}[/tex]
Learn more about unitary method: https://brainly.com/question/19423643
I hate these types of problems
I was never taught this stuff
Answers
Please help! I don't know what answer b is, but i know a, thank you.
Answers
They are corresponding angles
Step-by-step explanation:
We know that x=75⁰ because
[tex]180 - 105 = 75[/tex]
75⁰ is angle EFB
Since we know this, and because we know that AD//EH,
We can conclude that x=75⁰(AD is parallel to EH and angle CBA or x and angle EFB are corresponding angles)
The value of stock changes from $22 on Monday to $30 on Tuesday. Calculate the percent increase.
Answers
22 + 22 x r = 30
22 x r = 30 - 22
r = 8 : 22
r = +36,36%
r = increase rate
please help asap
For each relation, decide whether or not it is a function.
Answers
Answer:
Step-by-step explanation:
Refer to the definition of a function. I'll just give you a layman's definition to be concise.
For something to be a function, there needs to be exactly 1 output for every input. You cannot have a case where you input 1 value, and get 2 or more values as an output.
In math we call all the possible input values the domain, and we call all the possible output values the range.
Let's take a look at each situation on your worksheet.
1. Is a function. This is because only one arrow stems from each input value. There are cases where the different input values give the same output, sure, but each input returns 1 discrete thing, not an array of things.
(Think of it this way, if i had a machine that could answer any question I had with yes, no or maybe. I wouldn't want the machine to give me "yes and maybe" or "yes and no" as the result when I ask it a question. That doesn't make sense and I would think the machine is broken. What could happen, is that I ask the machine different questions, and for those different questions, it gave me the same answer, like "yes" and "yes" respectively. in that case, it would be acceptable, because it isn't contradicting itself for any individual question.)
2. Not a function. There are 2 different output values for b.
(Refer back to my machine analogy. The "machine" in this question is contradicting itself. I gave the machine one input, and the machine is telling me, "it's this and actually it's this other thing too")
3. Is a function for the same reasons as 1.
4. Isn't a function.
(It's basically telling you, the machine reads -6 as -4, but it also reads -6 as 0, and also 2. And it also tells you the machine reads -4 as -3, but it also reads it as 8. Again, the machine should only read 1 input in 1 way and not contradict itself. )
[tex] \sf \large \: find \: \frac{dy}{dx} \: if \: x=a ( \Theta + sin \Theta ) , y= a (1- Cos \Theta ) \: at \: \Theta = \frac{π}{2} \\ \\ \\ \\ \\ [/tex]
Kindly Don't Spàm!
Thanks!!!!
Answers
Given :
[tex] \: \: \: [/tex]
[tex] \rm \large \: x = a ( \Theta + Sin \Theta )[/tex][tex] \: \: \: [/tex]
[tex] \rm \large y = a ( 1 - cos \: \Theta )[/tex][tex] \: \: [/tex]
Now , x = a ( θ + sin θ )
[tex] \: \: [/tex]
Diff w.r.t " θ "
[tex] \: \: \: [/tex]
[tex] \rm \large\frac{dx}{dθ } = a \: \frac{d}{dθ} (θ + \sin\theta )[/tex][tex] \: \: [/tex]
[tex] \boxed{ \rm \large\underline{ \frac{dx}{d \theta} = a(1 + \cos \theta ) }}[/tex][tex] \: \: [/tex]
Now y = a ( 1-cosθ)
[tex] \: \: [/tex]
Diff w.r.t " θ " we get .
[tex] \: \: [/tex]
[tex] \rm \large \frac{dy}{d \theta} = a \frac{d}{d \theta} (1 - cos \theta) [/tex][tex] \: \: \: [/tex]
[tex] \boxed{ \rm \large \underline{ \frac{dy}{d \theta} = a \sin \theta}}[/tex][tex] \: \: \: [/tex]
From eqn ( 1 ) & ( 2 )
[tex] \: \: [/tex]
[tex] \rm \large \frac{dy}{dx} = \frac{ \frac{dy}{d \theta} }{\frac{dx}{d \theta}} [/tex][tex] \: \: \: [/tex]
[tex] \: \: \: \rm \large = \frac{ \cancel{a} \: sin \theta}{ \cancel a \: (1 + cos \theta)} [/tex][tex] \: \: [/tex]
[tex] \rm \large \: = \frac{sin \theta}{1 + \cos \theta } [/tex][tex] \: \: \: [/tex]
[tex] \rm \large \: \frac{2 \sin( \frac{\theta }{2} ) cos\frac{\theta }{2} }{2 \: cos ^{2} \frac{\theta }{2}} \: \: ......(sin \: a \: = 2 \: sin \frac{a}{2} \: cos \frac{a}{2} 1 + \: cos \: a \: = 2cos ^{2} \frac{a}{2} )[/tex][tex] \: \: [/tex]
[tex] \rm \large \: \frac{dy}{dx} = \frac{sin \frac{ \theta}{2} }{cos \frac{ \theta}{2} } [/tex][tex] \: \: [/tex]
[tex] \rm \large \: \frac{dy}{dx} = tan \frac{ \theta}{2} [/tex][tex] \: \: [/tex]
[tex] \rm \large \: ( \frac{dy}{dx} ) = tan \frac{ \frac{ \theta}{2} }{2} [/tex][tex] \: \: [/tex]
[tex] \rm \large \: = tan( \frac{ \theta}{4} )[/tex][tex] \: \: [/tex]
[tex] \boxed{ \rm \large \underline{ ( \frac{dy}{dx} ) = \frac{\pi}{2} = 1}}[/tex][tex] \: \: [/tex]
Hope Helps!:)
4x+y=2 solve for y algebra 2
Answers
-4x. -4x
y=2-4x
Answer:
Step-by-step explanation:
4x + y = 2
y = -4x + 2
What is the diameter of a hemisphere with the volume of 74466
Answers
[tex]\textit{volume of a hemisphere}\\\\ V=\cfrac{1}{2}\cdot \cfrac{4\pi r^3}{3}~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ V=74466 \end{cases}\implies 74466=\cfrac{1}{2}\cdot \cfrac{4\pi r^3}{3} \\\\\\ 74466=\cfrac{2\pi r^3}{3}\implies 223398=2\pi r^3\implies \cfrac{22398}{2\pi }=r^3\implies \cfrac{111699}{\pi }=r^3 \\\\\\ \sqrt[3]{\cfrac{111699}{\pi }}=r~\hfill \stackrel{\textit{diameter = 2r}}{2\sqrt[3]{\cfrac{111699}{\pi }}\implies \sqrt[3]{\cfrac{893592}{\pi }}}~~ \boxed{\approx~~65.77}[/tex]