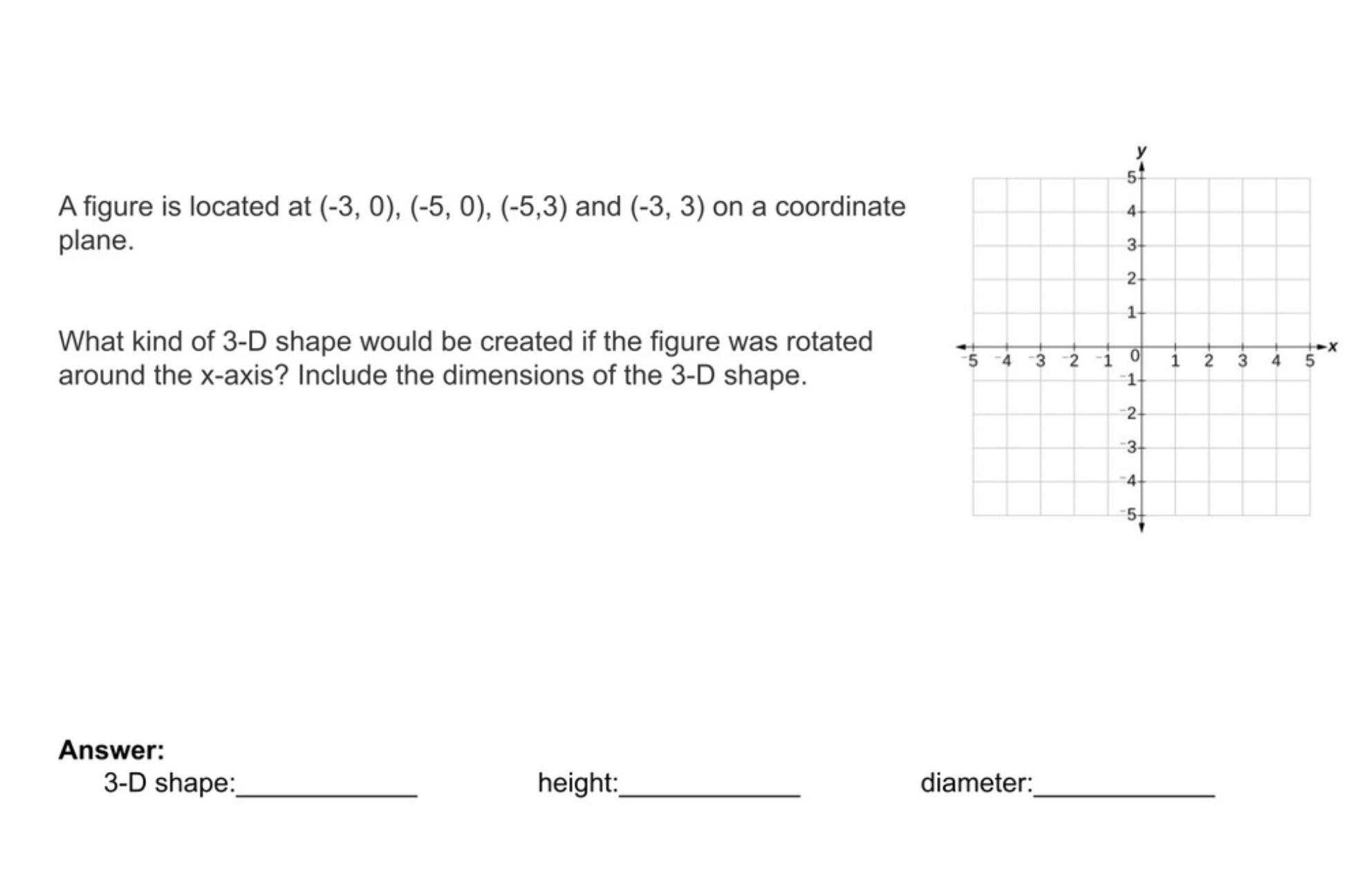
Answer: the 3d shape would be a rectangle. the hight is 3. and the diameter is 10
Step-by-step explanation:
the manager of a supermarket tracked the amount of time needed for customers to be served by the cashier. after checking with his statistics professor, he concluded that the checkout times are exponentially distributed with a mean of 5.5 minutes. what propotion of customers require more than 12 minutes to check out?
Approximately 0.357 or 35.7% of customers require more than 12 minutes to check out.
Since the checkout times are exponentially distributed with a mean of 5.5 minutes, we can use the exponential distribution formula to find the probability that a customer will take more than 12 minutes to check out:
P(X > 12) = 1 - P(X ≤ 12)
where X is the checkout time.
To find P(X ≤ 12), we can use the cumulative distribution function (CDF) of the exponential distribution, which is:
F(x) = 1 - e^(-λx)
where λ is the rate parameter of the distribution. For an exponential distribution with mean μ, the rate parameter λ is equal to 1/μ.
So, in our case, λ = 1/5.5 = 0.1818, and we can calculate P(X ≤ 12) as:
P(X ≤ 12) = F(12) = 1 - e^(-0.1818 × 12) ≈ 0.643
Therefore, the probability that a customer will take more than 12 minutes to check out is:
P(X > 12) = 1 - P(X ≤ 12) ≈ 1 - 0.643 ≈ 0.357
To learn more about statistics click on,
https://brainly.com/question/15291758
#SPJ4
The area of (V is 624.36 square meters. The area of sector
SVT is 64.17 square meters. Find the indicated measure.
1. The radius of V is approximately 14.04 meters.2.The circumference of V is approximately 88.24 meters. 3.mST arc is 26.85 degrees. 4.the length of ST arc is approximately 6.61 meters. 5.34.69 meters. 6.88.24m.
Describe Sector?In geometry, a sector is a part of a circle enclosed by two radii and an arc. Essentially, a sector is a slice of a circle. The two radii that form the sector are equal in length and share a common endpoint, which is the center of the circle. The arc of the sector is a portion of the circumference of the circle and its length is proportional to the measure of the central angle that it subtends.
We can use the given information to solve for the following:
1. Radius of V:
The area of a circle is given by the formula A = πr². We are given the area of V as 624.36 square meters, so we can solve for the radius r as:
A = πr²
624.36 = πr²
r² = 624.36/π
r ≈ 14.04 meters
Therefore, the radius of V is approximately 14.04 meters.
2. Circumference of V:
The circumference of a circle is given by the formula C = 2πr. Using the radius we just found, we can solve for the circumference of V as:
C = 2πr
C = 2π(14.04)
C ≈ 88.24 meters
Therefore, the circumference of V is approximately 88.24 meters.
3. mST arc:
The area of the sector SVT is given as 64.17 square meters. The area of a sector is given by the formula A = (θ/360)πr², where θ is the central angle of the sector in degrees. We are not given the value of θ, but we can solve for it as:
A = (θ/360)πr²
64.17 = (θ/360)π(14.04)²
θ ≈ 26.85 degrees
Therefore, the central angle of the sector SVT is approximately 26.85 degrees, and mST arc is also 26.85 degrees.
4. Length of ST arc:
The length of an arc of a circle is given by the formula L = (θ/360)C, where θ is the central angle of the arc in degrees, and C is the circumference of the circle. We can use the values we have already calculated to solve for the length of ST arc as:
L = (θ/360)C
L = (26.85/360)(88.24)
L ≈ 6.61 meters
Therefore, the length of ST arc is approximately 6.61 meters.
5. Perimeter of shaded region (sector):
The perimeter of a sector is the sum of the length of the arc and the lengths of the two radii that form the sector. Using the values we have already calculated, we can solve for the perimeter of the shaded sector as:
Perimeter = L + 2r
Perimeter = 6.61 + 2(14.04)
Perimeter ≈ 34.69 meters
Therefore, the perimeter of the shaded region (sector) is approximately 34.69 meters.
6. Perimeter of unshaded region (remaining circle part):
The perimeter of a circle is given by the formula C = 2πr. Using the radius we previously calculated, we can solve for the perimeter of the unshaded region as:
Perimeter = 2πr
Perimeter = 2π(14.04)
Perimeter ≈ 88.24 meters
Therefore, the perimeter of the unshaded region (remaining circle part) is approximately 88.24 meters.
To know more about length visit:
https://brainly.com/question/29141691
#SPJ1
pretty please helpppp
Answer: 2(n6)
And true states are
The two operations are mulitplication and substraction
The constants are 2 and 6
The expression is written as 2(n-6)
Step-by-step explanation:
Answer:
A,C,D,E should be correct.
A. Replace “a number” with the variable, n.
C. The two operations are multiplication and subtraction.
D. The constants are 2 and 6.
E. The expression is written as 2(n – 6).
hope this helped!
given that the absolute value of the difference of the two roots of $ax^2 + 5x - 3 = 0$ is $\frac{\sqrt{61}}{3}$, and $a$ is positive, what is the value of $a$?
The value of "a" is approximately 1.83 given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive.
We are given that the absolute value of the difference between the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive. We need to find the value of "a".
Let the two roots of the equation be r1 and r2, where r1 is not equal to r2. Then, we have:
|r1 - r2| = √(61) / 3
The sum of the roots of the quadratic equation is given by r1 + r2 = -5 / a, and the product of the roots is given by r1 × r2 = -3 / a.
We can express the difference between the roots in terms of the sum and product of the roots as follows:
r1 - r2 = √((r1 + r2)² - 4r1r2)
Substituting the expressions we obtained earlier, we have:
r1 - r2 = √(((-5 / a)²) + (4 × (3 / a)))
Simplifying, we get:
r1 - r2 = √((25 / a²) + (12 / a))
Taking the absolute value of both sides, we get:
|r1 - r2| = √((25 / a²) + (12 / a))
Comparing this with the given expression |r1 - r2| = √(61) / 3, we get:
√((25 / a²) + (12 / a)) = √(61) / 3
Squaring both sides and simplifying, we get:
25 / a² + 12 / a - 61 / 9 = 0
Multiplying both sides by 9a², we get:
225 + 108a - 61a² = 0
Solving this quadratic equation for "a", we get:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61)
Since "a" must be positive, we take the positive root:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61) ≈ 1.83
Therefore, the value of "a" is approximately 1.83.
Learn more about absolute value at
https://brainly.com/question/1301718
#SPJ4
The question is -
Given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive, what is the value of "a"?
Please help me with this homework
Answer:sasa
Step-by-step explanation:
Find the volume
of the figure below:
Step-by-step explanation:
Use Pythagorean theorem to find the base of the right triangle
221^2 = 195^2 + b^2
b = 104 km
triangle area = 1/2 base * height = 1/2 * 104 * 195 = 10140 km^2
Now multiply by the height to find volume
10140 km^2 * 15 km = 152100 km^3
Need answer by 11:45am
Question 8(Multiple Choice Worth 2 points)
(Creating Graphical Representations MC)
The number of milligrams of Vitamin C from 100 different gummy vitamins sold in the world was collected.
Which graphical representation would be most appropriate for the data, and why?
Box plot, because the median can easily be determined from the large set of data
Stem-and-leaf plot, because you can see the shape of the data
Histogram, because it shows each individual data point
Bar chart, because the data is categorical
Unlocked badge showing an astronaut’s boot touching down on the moon
See what the community says and unlock a badge
The graphical representation that is best and most appropriate for the data is Box plot, because the median can easily be determined from the large set of data. That is option A.
What is a box plot ?The box plot is a type of graphical representation of data that gIves more than one detail about the data set such as;
minimum, first quartile, median, third quartile, and maximum.Box plots allow you to compare multiple data sets better than others dues to the above listed features that it has.
Learn more about histogram here:
https://brainly.com/question/28164315
#SPJ1
1. Suppose we have the following annual risk-free bonds Maturity Price Coupon Rate YTM 1 98 0% 2.01% 2 101 2.48% 3 103 2.91% 4 101 2% 1.73% 5 103 5% 4.32% 39 a) Find the zero rates for all 5 maturities Note: for an extra challenge, try using lincar algebra to find == A + where 98 00 -- 3 103 0 2 2 5 5 0 104 2 0 0 0 0 0 0 1020 5 105 5 1 b) Suppose we have a risk-free security which pays cash flows of $10 in one year, $25 in two years, and $100 in four years. Find its price
a) The zero rates for the five maturities are: 1 year is 2.01%, 2 years is 2.48%, 3 years is 2.77%, 4 years is 1.73%, and 5 years is 4.32%.
b) The price of the security is $128.31.
a) To find the zero rates for all 5 maturities, we can use the formula for the present value of a bond:
PV = C / [tex](1+r)^n[/tex]
where PV is the present value,
C is the coupon payment,
r is the zero rate, and
n is the number of years to maturity.
We can solve for r by rearranging the formula:
r = [tex](C/PV)^{(1/n) }[/tex]- 1
Using the bond data given in the question, we can calculate the zero rates for each maturity as follows:
For the 1-year bond, PV = 98 and C = 0, so r = 2.01%.
For the 2-year bond, PV = 101, C = 2.48, and n = 2, so r = 2.48%.
For the 3-year bond, PV = 103, C = 2.91, and n = 3, so r = 2.77%.
For the 4-year bond, PV = 101, C = 2, and n = 4, so r = 1.73%.
For the 5-year bond, PV = 103, C = 5, and n = 5, so r = 4.32%.
Alternatively, we can use linear algebra to find the zero rates. We can write the present value equation in matrix form:
PV = A × x
where A is a matrix of coefficients, x is a vector of unknowns (the zero rates), and PV is a vector of present values.
To solve for x, we can use the equation:
x = ([tex]A^{-1}[/tex]) x PV
where ([tex]A^{-1}[/tex]) is the inverse of matrix A.
Using this method, we can solve for the zero rates as follows:
[2.01% ]
[2.48% ]
[2.77% ] = x
[1.73% ]
[4.32% ]
PV = [tex]A^{-1}[/tex] x [98]
[101]
[103]
[101]
[103]
PV = [-0.0201]
[ 0.0248]
[ 0.0277]
[-0.0173]
[ 0.0432]
b) To find the price of the security which pays cash flows of $10 in one year, $25 in two years, and $100 in four years, we can use the formula for the present value of a series of cash flows:
PV = [tex]C1/(1+r)^1 + C2/(1+r)^2 + C3/(1+r)^4[/tex]
where PV is the present value, C1, C2, and C3 are the cash flows, r is the zero rate, and the exponents correspond to the number of years until each cash flow is received.
Using the zero rates calculated in part (a), we can calculate the present value of each cash flow:
PV1 = $10 /(1+2.01 % [tex])^1[/tex] = $9.80
PV2 = $25/(1+2.48%[tex])^2[/tex] = $22.15
PV3 = $100/(1+1.73%[tex])^4[/tex] = $81.36
Then, the price of the security is the sum of the present values:
PV = $9.80 + $22.15 + $81.36 = $128.31
Therefore, the price of the security is $128.31.
For similar question on price of the security
https://brainly.com/question/29245385
#SPJ11
sue works 5 out of the 7 days of the week. how many possible schedules are there to work on tuesday or friday or both?
Sue works 5 out of 7 days a week, which implies that she has two days off. We need to discover how numerous conceivable plans there are for her to work on Tuesday or Friday or both.
There are two cases to consider:
1. Sue works on Tuesday as it were, Friday as it were, or both Tuesday and Friday.
2. Sue does not work on Tuesday or Friday.
For the primary case, there are three conceivable outcomes:
1. Sue works on Tuesday as it were and has Friday off.
2. Sue works on Friday as it were and has Tuesday off.
3. Sue works on both Tuesdays and Fridays.
For the moment case, there are two conceivable outcomes:
1. Sue works on one of the other 5 days of the week and has both Tuesday and Friday off.
2. Sue has Tuesday and Friday off.
In this manner, there are added up to 3 + 2 = 5 conceivable plans for Sue to work on Tuesday or Friday or both.
To know more about possible schedules for the week refer to this :
https://brainly.com/question/23689163
#SPJ4
true or false: we conduct a test of hypothesis by assuming that ha is correct, since that is the hypothesis we are trying to show is true. group of answer choices true false
Given statement "We conduct a test of hypothesis by assuming that ha is correct, since that is the hypothesis we are trying to show is true." is true. Because we start by assuming that the null hypothesis is correct, not the alternative hypothesis, when conducting a test of the hypothesis.
When conducting a test of hypothesis, we do not assume that Ha (the alternative hypothesis) is correct.
Instead, we begin by assuming that the null hypothesis (H0) is true.
The null hypothesis typically represents a statement of "no effect" or "no difference" between two groups or variables.
The alternative hypothesis (Ha) represents the statement we are trying to prove or gather evidence for but we must start with the assumption that the null hypothesis is correct.
State the null hypothesis (H0) and the alternative hypothesis (Ha).
The null hypothesis typically represents the status quo or a baseline assumption, while the alternative hypothesis represents the claim you want to prove or gather evidence for.
Determine the level of significance (α), which is the probability of rejecting the null hypothesis when it is actually true. Common significance levels are 0.05, 0.01, and 0.001.
Select an appropriate test statistic, which depends on the type of data and the hypothesis being tested. Examples include the t-test, chi-square test, and ANOVA.
Collect data and calculate the value of the test statistic based on the data.
Compare the calculated test statistic value to the critical value for the chosen level of significance.
If the test statistic is more extreme than the critical value, we reject the null hypothesis in favor of the alternative hypothesis.
Otherwise, we fail to reject the null hypothesis.
Hence, the statement is false.
For similar question on hypothesis.
https://brainly.com/question/27170372
#SPJ11
an airline passenger is planning a trip that involves three connecting flights that leave from airports a, b, and c, respectively. the first flight leaves airport a every hour, beginning at 8:00 a.m., and arrives at airport b 2 1/2 hours later. the second flight leaves airport b every 20 minutes, beginning at 8: 00 a.m., and arrives at airport c 1 1/6hours later. the third flight leaves airport c every hour, beginning at 8:45 a.m. what is the least total amount of time the passenger must spend between flights if all flights keep to their schedules?
An airline passenger is planning a trip with three connecting flights from airports A, B, and C.
The least total amount of time the passenger must spend between flights, assuming all flights keep to their schedules, is 55 minutes.
This occurs when the passenger takes the first flight from airport A at 8:00 a.m., arriving at airport B at 10:30 a.m., catches the second flight from airport B at 10:40 a.m., arriving at airport C at 11:50 a.m., and then takes the third flight from airport C at 12:45 p.m.
Learn more about airline:
https://brainly.com/question/29579489
#SPJ11
i need help with problem.
Answer:
[tex]y=5-2x[/tex]
Step-by-step explanation:
You have to give the equation in the form [tex]y=mx+c[/tex], where m is the gradient and c is the y-intercept (where the line crosses the y-axis).
From the graph, we can see the line crossed the y-axis at (0,5), so the y-intercept is (0,5), which means c is 5.
We can work out the gradient with the two points (2,1) and (1,3) by doing:
[tex]\frac{change in y}{change in x} =\frac{1-3}{2-1}=-2[/tex]
So the gradient of the line, m, is -2.
Thus the equation of the line is [tex]y=5-2x[/tex].
An expression is shown.
3(-12.5)
What is the value of the expression?
Answer: -37.5
Step-by-step explanation: You can simply do this in the calculator by doing 3 times -12.5. the parenthesis is a sign to multiply
Answer:
the answer is -75/2= - 37.5
A game requires players to roll a six-sided number cube and spin a spinner, like the one shown below. A circle shaped spinner divided in to 3 equal sections and named green ,blue, red. A needle is shown in center. Then, find the number of outcomes that represent rolling an odd number and landing on blue. What is the answer? 3 4 5 6? Please answer quick!!! I will get you Brainiest!!!
Using probability, there is only one outcome that represents rolling an odd number and landing on blue.
What exactly is probability?
Probability is a measure of the possibility or chance that an event will occur. It is represented by a number between 0 and 1, with 0 representing an improbable occurrence and 1 representing a certain event. A given event's probability is estimated by dividing the number of favourable outcomes by the total number of potential possibilities. Probability theory is frequently used to analyse and forecast the likelihood of occurrences in domains such as statistics, physics, economics, and finance.
Now,
The probability of rolling an odd number is 3/6, which can be simplified to 1/2. The probability of landing on blue= 1/3. Since the events of rolling an odd number and landing on blue are independent, we can multiply the probabilities to find the probability of both events occurring:
(1/2) × (1/3) = 1/6
So, there is only one outcome that represents rolling an odd number and landing on blue. The answer is 1.
To know more about probability visit the link
brainly.com/question/30034780
#SPJ1
How do you simplify this.
Answer:
[tex] \sqrt{7y} ( \sqrt{27y} + 5 \sqrt{12y} )[/tex]
[tex] \sqrt{7y} ( \sqrt{9} \sqrt{3y} + 5 \sqrt{4} \sqrt{3y} )[/tex]
[tex] \sqrt{7y} (3 \sqrt{3y} + 10 \sqrt{3y} )[/tex]
[tex]13 \sqrt{7y} \sqrt{3y} [/tex]
[tex]13y \sqrt{21} [/tex]
The range of which function is (2,00)?
O y = 2x
O y = 2(5*)
O y = 5x +2
O y = 5x + 2
The function which has range (2, ∞) is,
D) y = 5ˣ + 2
What is mean by Function?A relation between a set of inputs having one output each is called a function. and an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Now, For a function: y = 5ˣ
Range is,
⇒ ( 0 , + ∞ )
And, we have:
y = 5ˣ + 2 ,
which is translated 2 units up.
So, the range is ( 2, + ∞ ).
Hence, The function which has range (2, ∞) is,
D ) y = 5ˣ + 2
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ5
∠A=6x−2
∘
start color #11accd, angle, A, end color #11accd, equals, start color #11accd, 6, x, minus, 2, degrees, end color #11accd \qquad \green{\angle B} = \green{4x +48^\circ}∠B=4x+48
∘
, angle, B, equals, start color #28ae7b, 4, x, plus, 48, degrees, end color #28ae7b
Solve for xxx and then find the measure of \blueD{\angle A}∠Astart color #11accd, angle, A, end color #11accd:
The given information describes the measures of two angles, A and B. Angle A is represented as ∠A and has a measure of 6x-2 degrees. Angle B is represented as ∠B and has a measure of 4x+48 degrees. These measures are respectively shown in the colors #11accd and #28ae7b.
The question gives us two equations, one for angle A and one for angle B, in terms of x. We will have to solve for x and then find the measure of angle A.
To solve for x, we can set the expressions for ∠A and ∠B equal to each other and solve for x
∠A = ∠B
6x - 2 = 4x + 48
Subtracting 4x from both sides we get
2x - 2 = 48
Adding 2 to both sides we get
2x = 50
Dividing by 2 we get
x = 25
Now that we have found the value of x, we can substitute it into the expression for ∠A
∠A = 6x - 2
∠A = 6(25) - 2
By multiplying 6 with 25 we get
∠A = 150 - 2
By Subtracting we get
∠A = 148
Hence, the measure of angle A is 148 degrees.
To know more about information here
https://brainly.com/question/29043744
#SPJ4
An article on the relation of cholesterol levels in human blood to aging reports that average cholesterol level for women aged 70-74 was found to be 230m/dl. If the standard deviation was 20mg/dl and the distribution normal, what is the probability that a given woman in this age group would have a cholesterol level
a) Less than 200mg/dl
b) More than 200mg/dl
c) Between 190mg/dl and 210mg/dl
d) Write a brief report on the guidance you would give a woman having high cholesterol level in this age group
a) The probability of a given woman in this age group having a cholesterol level less than 200mg/dl is 6.68%.
b) The probability of a given woman in this age group having a cholesterol level more than 200mg/dl is 93.32%.
c) The probability of a given woman in this age group having a cholesterol level between 190mg/dl and 210mg/dl is 15.87%.
d) If a woman in this age group has a cholesterol level higher than 230mg/dl, it is considered high and puts her at risk of heart disease
To calculate the probability of a given woman in this age group having a cholesterol level less than 200mg/dl, we need to find the z-score first. The z-score is the number of standard deviations that a given value is from the mean. The formula to calculate the z-score is:
z = (x - μ) / σ
where x is the given value, μ is the mean, and σ is the standard deviation.
For a cholesterol level of 200mg/dl, the z-score is:
z = (200 - 230) / 20 = -1.5
We can then use a z-table or calculator to find the probability of a z-score being less than -1.5, which is 0.0668 or approximately 6.68%.
Next, to find the probability of a given woman in this age group having a cholesterol level more than 200mg/dl, we can use the same process but subtract the probability of a z-score being less than -1.5 from 1 because the total probability is always 1.
So, the probability of a given woman in this age group having a cholesterol level more than 200mg/dl is:
1 - 0.0668 = 0.9332 or approximately 93.32%.
Finally, to find the probability of a given woman in this age group having a cholesterol level between 190mg/dl and 210mg/dl, we need to find the z-scores for both values.
For a cholesterol level of 190mg/dl, the z-score is:
z = (190 - 230) / 20 = -2
For a cholesterol level of 210mg/dl, the z-score is:
z = (210 - 230) / 20 = -1
We can then use the z-table or calculator to find the probability of a z-score being between -2 and -1, which is 0.1587 or approximately 15.87%.
Finally, a brief report on the guidance that you would give a woman having high cholesterol levels in this age group is:
It is essential to make lifestyle changes such as eating a healthy diet, exercising regularly, quitting smoking, and managing stress to lower cholesterol levels.
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Hugo made a bunch of batches of pancakes for his summer camp. For each batch, Hugo used 1/3 cup of milk. Hugo used a total of 3 cups of milk. Let b represent the number of batches Hugo mad
The number of batches of pancakes made by Hugo using 3 cups of milk is equal to 9 batches.
Number of cups of milk used by Hugo for each batch = 1/3 cup of milk ,
The total amount of milk used for b batches would be,
Total milk = (1/3) × b
The total milk used was 3 cups,
Substitute the value in the equation we have,
⇒ (1/3) × b = 3
Solve for b we get,
Multiply both sides of the equation by the reciprocal of 1/3,
Reciprocal of ( 1/3 ) = 3/1 or simply 3
⇒ (1/3) × b × 3 = 3 × 3
⇒ b = 9
Therefore, Hugo made 9 batches of pancakes.
Learn more about batches here
brainly.com/question/856537
#SPJ4
The above question is incomplete, the complete question is:
Hugo made a bunch of batches of pancakes for his summer camp. For each batch, Hugo used 1/3 cup of milk. Hugo used a total of 3 cups of milk. Let b represent the number of batches Hugo made . Find the value of b?
. which one of the following statements is true? a. if you are given a sample percentage of 43%, you would need to know the sample size in order to convert this percentage to a proportion. b. the test statistic is affected by the size of the sample. c. the larger the p-value, the more evidence you have against the null hypothesis. d. we always begin a hypothesis test by assuming that the null hypothesis is false. e. none of the above statements are true.
If you are given a sample percentage of 43%, you would need to know the sample size in order to convert this percentage to a proportion.
The conversion formula is proportion = percentage/100. However, the proportion alone does not give information about the sample size, which is necessary for inference and hypothesis testing. The other statements are not true.
The test statistic is not affected by the sample size, but its value can be used to determine the significance of a hypothesis test. A larger p-value indicates weaker evidence against the null hypothesis, not stronger evidence. Finally, we assume the null hypothesis is true until we have sufficient evidence to reject it.
Learn more about percentage:
https://brainly.com/question/24304697
#SPJ11
A side of the triangle below has been extended to form an exterior angle of 67°. Find the value of xx.
Since a side of the triangle below has been extended to form an exterior angle of 67°, the value of x is equal to 52°.
What is the exterior angle theorem?In Mathematics, the exterior angle theorem or postulate can be defined as a theorem which states that the measure of an exterior angle in a triangle is always equal in magnitude (size) to the sum of the measures of the two remote or opposite interior angles of that triangle.
By applying the exterior angle theorem, we can reasonably infer and logically deduce that the sum of the measure of the two interior remote or opposite angles in the given triangle is equal to the measure of angle x (∠x);
∠y + 67° = 180°
∠y = 180° - 67°
∠y = 113°
∠x = 180° - (15° + 113°)
∠x = 52°
Read more on exterior angle theorem here: brainly.com/question/28034179
#SPJ1
A primary credit cardholder's card has an APR of 22. 99%. The current monthly balance, before interest, is $4,528. 34. Determine how much more the cardholder will pay, making monthly payments of $200, until the balance is paid off, instead of paying off the current balance in full
The cardholder will pay an additional $1,471.66 in interest by making monthly payments of $200 until the balance is paid off instead of paying off the current balance in full.
First, we need to calculate the total interest that will accrue on the current balance of $4,528.34. We can do this using the formula
Interest = Balance x (APR/12)
where APR is the annual percentage rate and is divided by 12 to get the monthly interest rate. Plugging in the values, we get:
credit card Interest = $4,528.34 x (22.99%/12) = $87.80
So the total interest that will accrue on the current balance is $87.80.
Next, we need to calculate how long it will take to pay off the balance by making monthly payments of $200. We can use a credit card repayment calculator to do this, but we'll use a simplified formula here
Months = -log(1 - (Balance x (APR/12))/Payment) / log(1 + (APR/12))
where Payment is the monthly payment amount. Plugging in the values, we get
Months = -log(1 - ($4,528.34 x (22.99%/12))/$200) / log(1 + (22.99%/12)) = 29.6 months
So it will take about 30 months (or 2.5 years) to pay off the balance by making monthly payments of $200.
Finally, we can calculate how much more the cardholder will pay in total by subtracting the current balance from the total amount paid over 30 months
Total amount paid = $200 x 30 = $6,000
Total interest paid = $6,000 - $4,528.34 = $1,471.66
Learn more about Credit card interest here
brainly.com/question/29641204
#SPJ4
What is the most upper (+3) or (-7)? Help please
Answer: Of the two numbers you provided, +3 is greater than -7. So, +3 is the most upper of the two numbers.
Answer: +3
Step-by-step explanation: Positive 3 is greater than negative 7. Therefore, +3 is the greater value.
n.2 multi-step word problems with positive rational numbers jvu you have prizes to reveal! go to your game board. on friday night, suzie babysat her cousin for 3 1 2 hours and earned $8.50 per hour. on saturday, she babysat for her neighbors for 4 1 2 hours. if she made a total of $72.50 from both babysitting jobs, how much did suzie earn per hour on saturday?
Answer:
$9.50
Step-by-step explanation:
You want Suzie's hourly rate on Saturday if she babysat for 3.5 hours on Friday, earning 8.50 per hour, and for 4.5 hours on Saturday, earning a total of 72.50 from both jobs.
EarningsFor (hours, rates) of (h1, r1) and (h2, r2), Suzie's total earnings for the two jobs are ...
earnings = h1·r1 +h2·r2
Filling in the known values, we can find r2:
72.50 = 3.5·8.50 +4.5·r2
72.50 = 29.75 +4.5·r2 . . . . . . . simplify
42.75 = 4.5·r2 . . . . . . . . . . . subtract 29.75
9.50 = r2 . . . . . . . . . . . . divide by 4.5
Suzie earned $9.50 per hour on Saturday.
__
Additional comment
The steps of the "multistep" problem are ...
find Friday's earningssubtract that from the total to find Saturday's earningsdivide by Saturday's hours to find the hourly rateEffectively, these are the steps to solving the equation we wrote.
On Sunday a local hamburger shop sold 356 hamburgers and cheeseburgers. The number of cheeseburgers sold was three times the number of hamburgers sold. How many hamburgers were sold on Sunday
The number of hamburgers sold on Sunday was 89
How many hamburgers were sold on SundayLet's assume that the number of hamburgers sold on Sunday was x.
According to the problem, the number of cheeseburgers sold was three times the number of hamburgers sold.
Therefore, the number of cheeseburgers sold can be expressed as 3x.
The total number of hamburgers and cheeseburgers sold was 356.
Therefore, we can write an equation to represent this information:
x + 3x = 356
Simplifying the left-hand side of the equation, we get:
4x = 356
Dividing both sides by 4, we get:
x = 89
Therefore, the number of hamburgers sold on Sunday was 89, and the number of cheeseburgers sold was 3 times that, or 267.
Read more about ratio at
https://brainly.com/question/21003411
#SPJ1
Evaluate the following.
Write an exponential function of the form y = ab^x that has the given points
(−1,6 3/4), (2, 1-4)
Answer:
Step-by-step explanation:
y = abx
a is the y-intercept
y = 16bx
Now substitute 2 for x and 1296 for y
1296 = 16(b)2
81 = b2
b = 9
y = 16(9)x
a production manager at a wall clock company wants to test their new wall clocks. the designer claims they have a mean life of 14 years with a variance of 16 . if the claim is true, in a sample of 40 wall clocks, what is the probability that the mean clock life would be less than 13.6 years? round your answer to four decimal places.
The probability that the mean clock life would be less than 13.6 years in a sample of 40 wall clocks is 0.1337
The probability that the mean clock life would be less than 13.6 years in a sample of 40 wall clocks can be calculated using the t-distribution since the population variance is unknown. The formula for t-distribution is:
t = (x-bar - μ) / (s / √n)
where x-bar is the sample mean, μ is the hypothesized population mean (14 years), s is the sample standard deviation (the square root of the sample variance), and n is the sample size (40).
Using the given variance, we can calculate the sample standard deviation as √16 = 4. Plugging in the values, we get:
t = (13.6 - 14) / (4 / √40) = -1.118
Using a t-distribution table with degrees of freedom (df) = n - 1 = 39, we find that the probability of getting a t-value less than -1.118 is 0.1337. Therefore, the probability that the mean clock life would be less than 13.6 years in a sample of 40 wall clocks is 0.1337 (rounded to four decimal places).
Learn more about probability
https://brainly.com/question/24756209
#SPJ4
The diameter of a circle is 12.5 cm. What is the circumference of the circle? Question 1 options: 19.63 cm 35. 25 cm 39.25 cm 78.5 cm please tell me quick!!!!
Answer:
The circumference of a circle is given by the formula:
C = πd
where C is the circumference, d is the diameter, and π is a mathematical constant approximately equal to 3.14.
In this case, the diameter of the circle is given as 12.5 cm.
Substituting this value into the formula, we get:
C = π(12.5)
C = 39.25 cm
Therefore, the circumference of the circle is 39.25 cm.
Hence, the answer is 39.25 cm.
The function f is given by f(x) = 10x + 3 and the function g is given by g(x) = 2×. For each question, show your reasoning
1. Which function reaches 50 first
2. Which function reaches 100 first?
1. x = 4.7 for f(x) and x = 25 for g(x), f(x) reaches 50 first.
2. x = 9.7 for f(x) and x = 50 for g(x), f(x) reaches 100 first.
1. Which function reaches 50 first?
To answer this, we need to solve for x in each function when the output is 50:
For f(x): 50 = 10x + 3
47 = 10x
x = 4.7
For g(x): 50 = 2x
x = 25
Since x = 4.7 for f(x) and x = 25 for g(x), f(x) reaches 50 first.
2. Which function reaches 100 first?
Similarly, we'll solve for x in each function when the output is 100:
For f(x): 100 = 10x + 3
97 = 10x
x = 9.7
For g(x): 100 = 2x
x = 50
Since x = 9.7 for f(x) and x = 50 for g(x), f(x) reaches 100 first.
for such more question on word problem
https://brainly.com/question/21405634
#SPJ11
Can y’all tell me 4 positive slope equations (y=mx+b)
Answer:
1. y = 4x + 2
2. y = 3x – 7
3. y = 7x + 6
4. y= 2x + 8
Step-by-step explanation:
1. y = 4x + 2
2. y = 3x – 7
3. y = 7x + 6
4. y= 2x + 8
These 4 equations have a positive slope because remember in the equation (y=mx+b) m = slope and since these equations have positive numbers in the m spot the slope of these equations are positive.