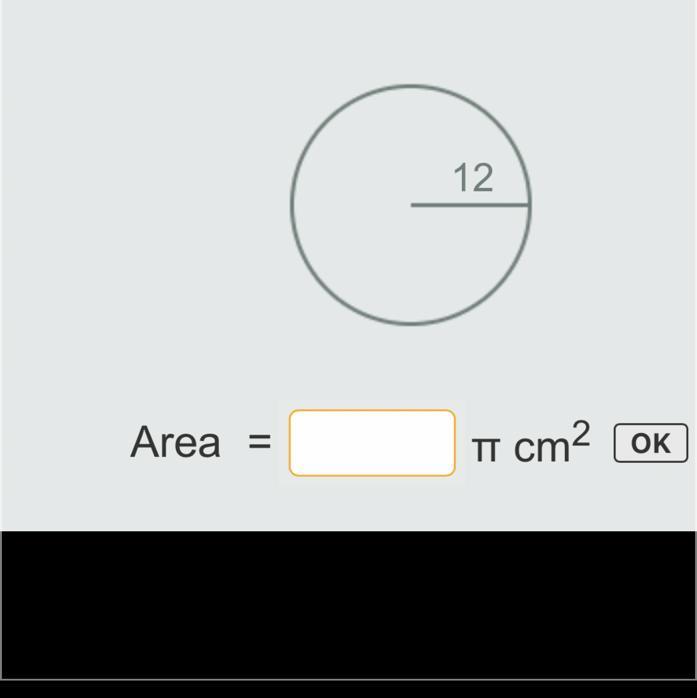
Answers
Answer: Area = 144 π cm²
Step-by-step explanation:
We can use this formula to find the area of a circle:
➜ r is equal to the radius, also known as half the width of a circle.
A = πr²
We will substitute our known values and solve for C by multiplying. Since the answer option includes π in our units, we do not multiply this into the 144.
A = πr²
A = π(12)²
A = 144 π cm²
Related Questions
if you used this version of the equation (including your new conversion factor, how would this have changed the intercept of your log-log graph? what would its value have been?
Answers
The equation with the new substitutions and conversion factor is a'B'T' = (1/6) * (2/3)^(1/3) * a^(1/3) * d^(1/2)*a^6/6 where k is (1/6) * (2/3)^(1/3) * a^(1/3) * d^(1/2) The intercept value of the log-log graph would have been -1.108.
Starting with Equation 4: T = ka^6/6, we can substitute a = (d/k)^(1/6) and b = (2/3)^(1/2) * (d/k)^(1/3) to get
T = k[(d/k)^(1/6)]^6/6
T = k(d/k)^(1/2)/6
T = (k^(1/2)/6) * d^(1/2)
Now we can rearrange the equation so that a, b, and t are on the left side
a'B'T' = ka^6/6
(a/d)^(1/6) * b^(2/3) * T' = k[(a/d)^(1/6)]^6/6 * T'
(a/d)^(1/6) * (2/3)^(1/2) * (d/k)^(1/3) * T' = (k^(1/2)/6) * d^(1/2) * T'
(2/3)^(1/2) * (a/d)^(1/6) * d^(1/3) * T' = (k^(1/2)/6) * d^(1/2) * T'
(2/3)^(1/2) * (a/d)^(1/6) * d^(1/3) = k^(1/2)/6
k = [(2/3)^(1/2) * (a/d)^(1/6) * d^(1/3)]^2/6
k = (1/6) * (2/3)^(1/3) * a^(1/3) * d^(1/2)
With this new conversion factor, the intercept of the log-log graph would have changed. The intercept represents the value of T when a = 1 (since log(1) = 0). Using the new conversion factor, we have
T = (1/6) * (2/3)^(1/3) * d^(1/2) * a^(1/3)
T = (1/6) * (2/3)^(1/3) * d^(1/2)
log(T) = log[(1/6) * (2/3)^(1/3) * d^(1/2)]
log(T) = log(1/6) + log[(2/3)^(1/3)] + log(d^(1/2))
log(T) = log(1/6) + (1/3) * log(2/3) + (1/2) * log(d)
So the intercept of the log-log graph would be log(1/6) + (1/3) * log(2/3) = -1.108, assuming that d is held constant. This intercept represents the value of log(T) when log(a) = 0, or when a = 1. In other words, when a = 1, the predicted value of T would be 0.162 (or 16.2% of its maximum value).
To know more about log graph:
https://brainly.com/question/17009226
#SPJ4
--The given question is incomplete, the complete question is given
" Plug the two substitutions into Equation 4 (T = ka^6/6)). Rearrange the equation so that a, b,t are on the left side of the equation and d remains on the right side, e.g. a'B'T' = ka^6/6 you will figure out what the "k" if you used this version of the equation (including your new conversion factor, how would this have changed the intercept of your log-log graph? what would its value have been?"--
2)
Phillip has 8 red balls, 3 green balls, 6 yellow balls, 3 orange balls, 13 black balls
and 15 blue balls in his bag.
Mean: | 0,2, Median :
Mode:
Range
Answers
The results of the balls in Phillip's bag are:
The mean = 8.
The median = 7.
The mode = blue
The range = 12
How do we calculate the Mean, Median, Mode and Range?The mean (or the average) is the sum of all the values divided by the total number of values. Let's calculate the mean for the given data:
Total number of balls = 8 + 3 + 6 + 3 + 13 + 15 = 48
Mean = (8 + 3 + 6 + 3 + 13 + 15) / 6 = 48 / 6 = 8
Mean = 8.
The median is the middle value when a set of values is arranged in ascending or descending order.
Let's arrange the given data in ascending:
3, 3, 6, 8, 13, 15
As the total number of values is even, the median will be the average of the two middle values, which are 6 and 8.
Median = (6 + 8) / 2 = 7
The median = 7.
The mode is the value that appears most frequently in a set of values. Let's find the mode of the given data:
Red balls: 8
Green balls: 3
Yellow balls: 6
Orange balls: 3
Black balls: 13
Blue balls: 15
Blue balls have the highest frequency (i.e., 15) among all the colors.
The range is the difference between the highest and lowest values in a set of values. Let's find the range of the given data:
Highest value = 15 (blue balls)
Lowest value = 3 (green balls and orange balls)
Range = Highest value - Lowest value = 15 - 3 = 12
Range = 12.
Learn more about the mean at brainly.com/question/1136789
#SPJ1
The shaded area of a circle is 25 cm squared. if the diameter of the circle is 10cm, determine what percentage of the circle is shaded
Answers
If the shaded area of a circle is 25 cm squared. if the diameter of the circle is 10cm, the percentage of the circle is shaded is: 31.83% .
What percentage of the circle is shaded?We can start by finding the area of the entire circle. The formula for the area of a circle is:
A = πr^2
where A is the area and r is the radius. Since the diameter of the circle is 10 cm, the radius is half of that, or 5 cm. Therefore, the area of the entire circle is:
A = π(5 cm)^2 = 25π cm^2
Next, we can find what percentage of the circle is shaded by dividing the shaded area by the total area of the circle and multiplying by 100:
Percentage shaded = (shaded area / total area) x 100
Percentage shaded = (25 cm^2 / 25π cm^2) x 100
Percentage shaded = 100 / π ≈ 31.83%
Therefore, approximately 31.83% of the circle is shaded.
Learn more about percentage of the circle here:
https://brainly.com/question/23082370
#SPJ1
Mark earns $8 per hour at a store.
Part A: Write an equation for this situation.
Part B: Create a table. Use h for hours worked and p for pay in dollars.
Part C: What part of your rule shows the number of hours Mark worked?
Part D: One week Mark earned $168. How many hours did he work that week?
Part E: Explain whether or not the equation is a direct variation.
Answers
p=8h is the equation.This part is represented in tabular form.The coefficient of h. Mark worked 21 hours that week.Yes, the equation is a direct variation.
What is an equation?An equation is a statement that shows the equality of two expressions. It typically contains one or more variables and may involve mathematical operations such as addition, subtraction, multiplication, and division. Equations are commonly used in mathematics, science, and engineering to model real-world situations and solve problems.
Define direct variation?Direct variation is a mathematical relationship between two variables, where a change in one variable results in a proportional change in the other variable. In other words, if two variables are in direct variation, when one variable increases, the other variable increases as well, and when one variable decreases, the other variable decreases as well, in a constant ratio.
Part A: The equation for this situation is p = 8h, where p represents the pay in dollars and h represents the number of hours worked.
Part B:
| Worked (hrs) | Pay (p) |
|------------------|---------|
| 1 | 8 |
| 2 | 16 |
| 3 | 24 |
| 4 | 32 |
| 5 | 40 |
| 6 | 48 |
and so on.
Part C: The coefficient of h, which is 8, shows the number of hours Mark worked.
Part D: We can use the equation p = 8h and substitute p = 168 to find the number of hours Mark worked.
168 = 8h
h = 21
Therefore, Mark worked 21 hours that week.
Part E: Yes, the equation is a direct variation because the pay (p) is directly proportional to the number of hours worked (h) and the constant of variation is 8.
Learn more about direct variation here:
https://brainly.com/question/13977805
#SPJ1
Harry is organizing a picnic. He can spend at most $24. 00 on beverages. Iced tea costs $2. 00 per gallon and lemonade costs $2. 50 per gallon. If x represents the number of gallons of iced tea and y represents the number of gallons of lemonade, which inequality shows the number of gallons of each drink that he can buy? Identify the number of gallons of iced tea that Harry can buy if he buys 5 gallons of lemonade.
Answers
Some working out:
5y = (2.50x5)
5y = 12.50 (lemonade)
24-12.50 = 11.50
11.50/2 = 5 r 1.5
Therefore Harry can buy 5 gallons of lemonade and 5 gallons of iced tea and still have $1.50 left over from his original $24 dollar budget
Answer:
Harry can buy 5 gallons of lemonade and 5 gallons of iced tea and still have $1.50 left over from his original $24 dollar budget
Step-by-step explanation:
professional scouts are timing a football player running a 40-yard dash to determine how his speed compares to other players they may want on their team. what type of analysis are the scouts using?
Answers
The scouts are using quantitative analysis.
A 10-ft chain weighs 25 lb and hangs from a ceiling. Find the work done (in ft-lb) in lifting the lower end of the chain to the ceiling so that it is level with the upper end.
Answers
The work done in lifting the lower end of the chain to the ceiling so that it is level with the upper end is 250 ft-lb.
The work done in lifting the lower end of the chain to the ceiling can be calculated using the formula for work, which is given by:
Work = force x distance
In this case, the force is the weight of the chain, which is 25 lb, and the distance is the length of the chain, which is 10 ft.
So, the work done in lifting the lower end of the chain to the ceiling is:
Work = 25 lb x 10 ft
Work = 250 ft-lb
Therefore, the work done in lifting the lower end of the chain to the ceiling so that it is level with the upper end is 250 ft-lb.
Learn more about “ lifting the lower end “ visit here;
https://brainly.com/question/14802857
#SPJ4
The work done in lifting the lower end of the chain to the ceiling so that it is level with the upper end is 125 ft-lb.
The work done in lifting the lower end of the chain to the ceiling so that it is level with the upper end is 125 ft-lb.
To find the work done in lifting the lower end of the chain to the ceiling, we need to consider the average weight of the chain as it is being lifted.
1. First, find the weight per foot of the chain:Weight of chain = 25 lbLength of chain = 10 ftWeight per foot = (25 lb) / (10 ft) = 2.5 lb/ft2.
Determine the average weight being lifted:Since you're lifting the chain from one end, the average weight you're lifting is half of the chain's total weight.
Average weight = (25 lb) / 2 = 12.5 lb3. Calculate the work done:Work done = Force x DistanceForce = Average weight = 12.5 lbDistance = Length of chain = 10 ftWork done = (12.5 lb) x (10 ft) = 125 ft-lb
So, the work done in lifting the lower end of the chain to the ceiling so that it is level with the upper end is 125 ft-lb.
to learn more about average weight click here:
brainly.com/question/27154543
#SPJ11
at what rate is the base of the triangle changing when the altitude is 20 cm and the area is 120 cm2?
Answers
The rate at which the base of the triangle is changing when the altitude is 20 cm and the area is 120 cm^2 is 0 cm/s.
To solve this problem, we need to use the formula for the area of a triangle, which is:
A = (1/2)bh
Where A is the area, b is the base, and h is the altitude.
We know that the area is 120 cm^2 and the altitude is 20 cm. So we can plug in these values and solve for the base:
120 = (1/2)b(20)
240 = 20b
b = 12 cm
Now we need to differentiate both sides of the equation with respect to time (t):
dA/dt = (1/2)(db/dt)h
We are given the value of dh/dt (which represents the rate at which the altitude is changing) is 3 cm/s. We need to find db/dt (which represents the rate at which the base is changing).
Plugging in the values we know, we get:
dA/dt = (1/2)(db/dt)(20)
Solving for db/dt, we get:
db/dt = (2dA/dt)/h
Plugging in the values we know, we get:
db/dt = (2)(0)/20
db/dt = 0 cm/s
Since the area is constant (120 cm²) and the altitude is constant (20 cm), the base of the triangle is not changing. Therefore, the rate at which the base is changing is: 0 cm/s
Learn about application of derivatives here: brainly.com/question/25120629
#SPJ11
PLS HURRY!!
The length of ribbons found at a seamstress are listed. 3, 6, 9, 11, 12, 13 What is the appropriate measure of variability for the data shown, and what is its value?
Answers
Thus, the appropriate measure of variability found for the given data is 10.
Explain about the range of the data:The difference here between maximum and smallest values in a data set is known as the range. Utilizing the exact same units as the data, it measures variability. More variability is shown by larger values.
The range in statistics refers to the distribution of your data between the lowest and greatest value in the distribution. It is a widely used indicator of variation. Measures of variability provide you with descriptive statistics for summarising your data set in addition to measurements of central tendency.Given length of ribbons:
3, 6, 9, 11, 12, 13
Minimum value = 3
Maximum value = 13
Actually, the range, which is determined by deducting the lowest value from the greatest value in the dataset, would be the proper measure of variability for this data.
Range = Maximum value - Minimum value
Range = 13 - 3
Range = 10
Thus, the appropriate measure of variability found for the given data is 10.
Know more about the range of the data:
https://brainly.com/question/24326172
#SPJ1
Find the 11th term of the geometric sequence shown below.
-9x²,-18x7, -36x¹2
12
"...
Answers
the 11th term in the given geometric sequence is equal to [tex]-9216x^{52}[/tex]
What is a geometric sequence.A sequence is a list of numbers indexed by the natural numbers 1,2,3,4,5.. A common notation for a sequence is [tex]a_1,a_2,a_3,\cdots[/tex]. Most often for interesting sequences there is some pattern in the list of numbers, and there is some formula to generate the nth number in the sequence. A sequence is called a geometric sequence if the next number number is got from the previous number by multiplying it by a fixed number r. This number is called the common ratio r of the sequence. So if the first number is a, then the second number is ar, the third is [tex]ar^2[/tex]... So that the nth number [tex]a_n = ar^{n-1][/tex].
For example 1 ,3,9,27,81,.... The sum of the first n terms of such a sequence is equal to [tex]$S_n = \frac{a(r^n-1)}{r-1}$[/tex]. if the absolute value of r, [tex]|r| < 1[/tex], then the sum to infinity is [tex]$S = \frac{a}{1-r}$[/tex].
In our question we are given a geometric sequence whose first term :
[tex]$a = -9x^2\,,\textrm{ and common ratio : r } = 2x^5$[/tex] .
So the 11th term is [tex]$ar^{10} = (-9x^2){(2x^5)}^{10} = (-9x^2)(1024x^{50}) = -9216x^{52}$[/tex]
To know more about geometric sequences, visit:
https://brainly.com/question/13008517
#SPJ1
Please help me with this homework
Answers
Answer: Circumference = 18 π cm
Step-by-step explanation:
We can use this formula to find the circumference of a circle:
➜ r is equal to the radius, also known as half the width of a circle.
C = 2πr
We will substitute our known values and solve for C by multiplying. Since the answer option includes π in our units, we do not multiply this into the 18.
C = 2πr
C = 2π(9)
C = 18 π cm
Answer: 18π
Step-by-step explanation:
The circumference of a circle is equal to 2πr, with r being equal to the radius. The radius of a circle is defined as the length from any point on the circle to its middlemost point. In this case, we are given the value of the radius as defined by the line. The radius equals 9, which we can plug into the equation.
C= 2πr
C = 2π(9)
C = 18π = 56.55
Hope this helps!
if x is a nonnegative real number, then the expression √ x is called the
Answers
If x is a non-negative real number, then the expression √ x is called the Principal square root. The answer is Principal Square Root.
What is Principal Square Root?
The positive square root of a non-negative real integer is the principal square root. It is the one and only non-negative real number that, when squared, yields the given non-negative real number. The principal square root of 9 is 3, for example, because 3 multiplied by itself equals 9.
The radical sign (√) is frequently used to represent the principal square root. The term √x denotes Principal square root of x. The sign can be used to indicate the negative square root of x in some settings, but this is less frequent.
The principal square root notion is significant in mathematics, including algebra, geometry, and calculus. It's used to solve equations, simplify expressions, and calculate lengths and distances. It's also used in a wide range of scientific and engineering applications.
Therefore, if x is a non-negative real number, then the expression √ x is called the Principal square root.
Learn more about Principal Square Root:
https://brainly.com/question/29775049
#SPJ4
If x is a nonnegative real number, then the expression √ x is called the square root of x. The square root of a nonnegative real number is a value that, when multiplied by itself, equals the original number.
If x is a nonnegative real number, then the expression √x is called the "principal square root" of x. The principal square root of a nonnegative real number x is the nonnegative real number that, when multiplied by itself, equals x. In other words, if y = √x, then y * y = x. This ensures that the result is also a nonnegative real number.
For example, the square root of 4 is 2 because 2 multiplied by 2 equals 4. The square root function is denoted by the symbol √ and is used to find the positive number that, when squared, gives the input value.
To learn more about principal square root: brainly.com/question/29775310
#SPJ11
Springtown Hardware kept an inventory of 697,500 lawnmowers in the past. With a change in management, the hardware store now keeps an inventory of 24% more lawnmowers. How many lawnmowers is that?
Answers
Thus, the number of current lawnmowers in the Springtown Hardware is 864,900.
Explain about the percentage:In mathematics, a percentage is a number or ratio that may be expressed as a fraction of 100. The Latin word "per centum," which meaning "per 100," is where the word "percent" comes from. % is the symbol used to represent percentages.
When a number is expressed in decimal form, you can calculate its percentage by multiplying it by 100. For instance, multiplying 0.5 by 100 gives you the percentage 50%.
Given data:
Springtown Hardware's inventory - 697,500 lawnmowers.
Current inventory of 24% more lawnmowers.
Current inventory = old inventory + 24% of old inventory
Current inventory = 697,500 + 24 % of 697,500
Current inventory = 697,500 + 24 * 697,500/ 100
Current inventory = 697,500 + 24* 6,975
Current inventory = 864,900
Thus, the number of current lawnmowers in the Springtown Hardware is 864,900.
Know more about the percentage:
https://brainly.com/question/24877689
#SPJ1
state the name for this figure...50 points
Answers
Answer: Trapezoid
Step-by-step explanation:
Answer:
it's also called a quadrilateral with 1 right angle
Solve the IVP given by y''+y=t, y(0)=1, y'(0)=-2
Answers
The solution to the IVP given by y''+y=t, y(0)=1, y'(0)=-2 is y(t) = cos(t) - (3/2) sin(t) + (1/2) t.
To solve the Initial Value Problem, we can use the method of undetermined coefficients, which involves assuming a particular form for the solution to the non-homogeneous equation y'' + y = t, and then finding the coefficients of the terms in that form by substituting it back into the equation.
First, we find the general solution to the homogeneous equation y'' + y = 0
The characteristic equation is r² + 1 = 0, which has solutions r = ±i. Therefore, the general solution to the homogeneous equation is
y_h(t) = c₁ cos(t) + c₂ sin(t),
where c₁ and c₂ are constants determined by the initial conditions.
Next, we assume a particular form for the non-homogeneous solution, based on the form of the right-hand side t. Since t is a linear function, we assume that the particular solution has the form
y_p(t) = a t + b.
Substituting this into the differential equation, we get
y''_p + y_p = t
2a + (at+b) = t.
Equating coefficients, we get
a = 1/2, b = 0.
Therefore, the particular solution is
y_p(t) = (1/2) t.
The general solution to the non-homogeneous equation is then the sum of the homogeneous and particular solutions
y(t) = y_h(t) + y_p(t)
= c₁ cos(t) + c₂ sin(t) + (1/2) t.
To determine the constants c₁ and c₂, we use the initial conditions:
y(0) = c₁ cos(0) + c₂ sin(0) + (1/2) (0) = c₁ = 1,
y'(0) = -c₁ sin(0) + c₂ cos(0) + (1/2) (1) = c₂ - (1/2) = -2,
so c₂ = -3/2.
Therefore, the solution to the IVP is
y(t) = cos(t) - (3/2) sin(t) + (1/2) t.
Learn more about Initial Value Problem here
brainly.com/question/30547172
#SPJ4
Practice & Problem Solving Leveled Practice 7. What is the surface area of the cylinder represented by the net? Uses as part of your answer 10 ft 16 ft
Answers
the surface area of the cylinder represented by the given net is approximately 166.306 square feet.
What is the surface area of the cylinder?To calculate the surface area of a cylinder using its net, we need to identify the different components of the net and their measurements.
Without the specific net provided, I will assume a standard net of a cylinder, consisting of two circles for the top and bottom faces, and a rectangle for the lateral (side) surface.
Given that the measurements provided are 10 ft and 16 ft, we can assume that the height of the cylinder is 10 ft and the circumference of the circular bases is 16 ft.
The surface area of a cylinder is given by the formula:
Surface Area [tex]= 2 \times \pi \times r \times (r + h)[/tex]
where r is the radius of the circular base and h is the height of the cylinder.
Since the circumference of the circular base is given as 16 ft, we can calculate the radius (r) using the formula:
Circumference [tex]= 2 \times π times r[/tex]
[tex]16 = 2 \times π \times r[/tex]
[tex]r = 16 / (2 \times \pi)[/tex]
[tex]r v\ approx 2.546 ft[/tex] (rounded to three decimal places)
Now that we know the radius (r) and the height (h) of the cylinder, we can substitute these values into the formula for surface area:
Surface Area [tex]= 2 \times π \times 2.546 \times (2.546 + 10)[/tex]
Surface Area [tex]\approx 166.306 ft^2[/tex] (rounded to three decimal places)
Therefore, the surface area of the cylinder represented by the given net is approximately [tex]166.306[/tex] square feet.
Learn more about cylinder here:
https://brainly.com/question/16134180
#SPJ1
Prism A and prism B are similar. The volume of prism A is 27 cubic units while the volume of prism B is approximately 512 cubic units. If the surface area of prism B is 128 square units, what is the surface area of prism A?
Answers
Answer:
Surface area of prism A is approximately 12.4 square units.
Step-by-step explanation:
Since prism A and prism B are similar, their corresponding side lengths are proportional. Let's use the scale factor k to represent the ratio of the side lengths of prism B to those of prism A. Then, the volume of prism B is (k³)(27) = 27k³ cubic units. Similarly, the surface area of prism B is (k²)(surface area of prism A).
We are given that the volume of prism B is approximately 512 cubic units. Therefore, we can solve for k:
27k³ = 512
k³ = 512/27
k ≈ 3.62
Now, we can use k to find the surface area of prism A:
surface area of prism B = (k²)(surface area of prism A)
128 = (3.62²)(surface area of prism A)
surface area of prism A ≈ 12.4 square units
Therefore, the surface area of prism A is approximately 12.4 square units.
Find the 49th term.
-15, -10, -5, O, 5, ...
49th term = [?]
1st term + common difference(desired term - 1)
Enter
Answers
Answer:
49th term = 225
Step-by-step explanation:
The following sequence: -15, -10, -5, 0, -5... is an example of an arithmetic progression.
An arithmetic progression or AP for short, is a sequence in which the difference between successive terms is constant. This difference is known as the common difference, and can be found by subtracting a term by its preceding term.
The general formula, for the nth term of an arithmetic progression, is thus:
Tn = a + (n - 1)d, where a = first term, and d = common difference.
In the sequence: -15, -10, -5, 0, 5...,
a = -15, and d = -10--15 = 5
T49 = -15 + (49 - 1)5 = 225
∴ 49th term = 225
by considering the curve traced by the parametrisation z(t) = t 2 it3 with −1 ≤ t ≤ 1, show why the condition that z ′ (t) never vanishes is necessary to ensure that smooth curves have no cusps.
Answers
To ensure that smooth curves have no cusps, we need to require that z'(t) never vanishes. This condition ensures that the tangent line to the curve changes smoothly and continuously as we move along the curve, without any abrupt changes in direction that would create cusps.
To understand why the condition that z'(t) never vanishes is necessary to ensure that smooth curves have no cusps, we first need to understand what a cusp is. A cusp is a point on a curve where the tangent line changes direction abruptly, creating a sharp point or corner in the curve.
Now, let's consider the curve traced by the parametrization z(t) = t^2it^3 with -1 ≤ t ≤ 1. To determine whether this curve has any cusps, we need to calculate the derivative of z(t) with respect to t:
z'(t) = 2it^3 + 3t^2i
If we set z'(t) equal to zero and solve for t, we get:
2it^3 + 3t^2i = 0
t^2(2i t + 3i) = 0
This equation has two solutions: t = 0 and t = -3/2i. These are the points on the curve where z'(t) vanishes.
At t = 0, the curve passes through the origin, which is a smooth point. However, at t = -3/2i, the curve has a cusp. To see why, we can look at the behavior of z(t) near this point.
As t approaches -3/2i from either side, the magnitude of t^2 increases without bound, while the magnitude of t^3 remains constant. This means that z(t) approaches infinity along a straight line with slope -3/2i. In other words, the curve has a sharp corner or cusp at this point.
To learn more about tangent visit;
brainly.com/question/30260323
#SPJ11
‼️WILL MARK BRAINLIEST‼️
Answers
The average distance of electric cars is 275.
The range of the data set is 300.
How to solveGiven:
Average of the data set = 275Range of the data set = 300To find: Average distance of electric cars
Solution:
The average distance of electric cars can be calculated by finding the average of the data set containing the distances of electric cars. Let's assume that the data set is as follows:
250, 250, 250, 400, 300, 300, 350, 100
To find the average distance of electric cars, we can use the formula:
Average = (Sum of all the data points) / (Number of data points)
Substituting the given values, we get:
Average = (250 + 250 + 250 + 400 + 300 + 300 + 350 + 100) / 8
Average = 2200 / 8
Average = 275
Therefore, the average distance of electric cars is 275.
Now, let's calculate the range of the data set. The range is the difference between the maximum and minimum values in the data set. From the given data set, we can see that the minimum value is 100 and the maximum value is 400.
Range = Maximum value - Minimum value
Range = 400 - 100
Range = 300
Therefore, the range of the data set is 300.
Read more about range here:
https://brainly.com/question/24326172
#SPJ1
Triangle ABC with vertices at A(4, 3), B(3, −2), C(−3, 1) is dilated using a scale factor of 3.5 to create triangle A′B′C′. Determine the vertex of point C′.
C′(−10.5, 1)
C′(−10.5, 3.5)
C′(−3, 3.5)
C′(−10.5, −3.5)
Answers
The correct option is C′(−10.5, 3.5) i.e. the vertex of point C′ is (-10.5, 3.5).
What is dilation?
In mathematics, dilation is a type of transformation that changes the size of a geometric object, but not its shape or orientation. Dilation is similar to scaling, but it involves a fixed point called the center of dilation, and a scale factor that determines the degree of expansion or contraction.
To determine the vertex of point C′, we need to apply the dilation transformation to the coordinates of the original vertex C(-3,1) using a scale factor of 3.5.
The coordinates of C′ can be found by multiplying the coordinates of C by the scale factor:
C′ = (3.5)C = (3.5)(-3,1) = (-10.5,3.5)
Therefore, the vertex of point C′ is (-10.5, 3.5).
Thus, the correct option is C′(−10.5, 3.5).
To learn more about dilation visit the link:
https://brainly.com/question/3457976
#SPJ1
Find a congruence transformation that maps triangle RST to triangle UVW
Answers
A congruence transformation that maps triangle RST to triangle UVW is a reflection along the line y = 1, followed by a translation 2 units right and down by 1 units.
A congruence transformation that maps triangle RST to triangle UVW is a rotation of 180°, followed by a translation 2 units left and down by 5 units.
What is a transformation?In Mathematics and Geometry, a transformation is the movement of a point from its initial position to a new location. This ultimately implies that, when a geometric figure or object is transformed, all of its points would also be transformed;
What is a reflection?In Mathematics and Geometry, a reflection can be defined as a type of transformation which moves every point of the geometric figure such as a triangle, by producing a flipped, but mirror image of the geometric figure.
By critically observing the geometric figures, we can reasonably infer and logically deduce that the pre-image underwent a sequence of congruence transformation to produce the image.
Read more on transformation here: https://brainly.com/question/10754933
#SPJ1
Can please someone help me ASAP? It’s due tomorrow. I will give brainliest if it’s all correct!!
Please do part a, b, and c
Answers
The sample space are:
{AR, AS, AT, AE, RA, RS, RT, RE, SA, SR, ST, SE, TA, TR, TS, TE, EA, ER, ES, ET}
The favorable outcomes care:
{RS, RT, SR, ST, TR, TS}
The probability is 0.3 or 30%
How to find the sample spacePart A:
The sample space represents all possible outcomes that can occur when two cards are randomly selected without replacement from the given pile of cards.
The sample space can be represented as follows:
{AR, AS, AT, AE, RA, RS, RT, RE, SA, SR, ST, SE, TA, TR, TS, TE, EA, ER, ES, ET}
Part B:
The favorable outcomes are those outcomes in which both cards are consonants. In this case, the consonants are R, S, and T.
The favorable outcomes can be represented as follows:
{RS, RT, SR, ST, TR, TS}
Part C:
To calculate the probability of selecting 2 cards that are consonants, we need to find the ratio of favorable outcomes to the sample space.
The number of favorable outcomes is 6, and the size of the sample space is 20.
Therefore, the probability of selecting 2 cards that are consonants is:
P(consonants) = favorable outcomes / sample space
P(consonants) = 6 / 20
P(consonants) = 0.3 or 30%
Learn more about sample space at
https://brainly.com/question/10558496
#SPJ1
The dimensions of a triangular prism are given in the diagram find the volume of the prism in cubic feet
Answers
The volume of the prism is gotten as 312 cm³.
What is volume?Volume is described as a measure of three-dimensional space. It is often quantified numerically using SI derived units or by various imperial or US customary units.
The basic formula for volume is length × width × height.
The formula for the volume of triangular prism = area of triangle x length
area of triangle = 1/2 x base x height
⇒ area of triangle = 1/2 x 8 x 6 = 24 cm²
Therefore, volume of the prism = 24 x 13 = 312 cm³
Learn more about volume at: https://brainly.com/question/27710307
#complete question is shown in the diagram
#SPJ1
ASAP Please help me do a two column proof for this. I am struggling
Answers
∠A = ∠C in trapezoid ABCD with arcAB = arcCD, can be proven with the property of isosceles triangles.
How to prove the relation?Since arcAB = arcCD, the lengths of the two arcs are equal. This implies that the lengths of the segments subtended by these arcs, AB and CD, are also equal.
Let E and F be the midpoints of the non-parallel sides AD and BC, respectively. Connect E and F with a line segment EF.
Since E and F are midpoints, DE = EA and BF = FC. In addition, since AB = CD = L, we can say that:
DE + EA = BF + FC
EA = FC
So, by the Hypotenuse-Leg (HL) theorem of congruence, triangles AEF and CFE are congruent:
ΔAEF ≅ ΔCFE
Now, since the triangles are congruent, their corresponding angles are equal:
∠A = ∠C
Find out more on trapezoids at https://brainly.com/question/26303997
#SPJ1
Which sequence of transformations produces R’S’T’ from RST?
On a coordinate plane, triangle R S T has points (0, 0), (negative 2, 3), (negative 3, 1). Triangle R prime S prime T prime has points (2, 0), (0, negative 3), (negative 1, negative 1).
Answers
the sequence of transformations that produces R'S'T' from RST is translation 2 units to the right and 3 units down, followed by a rotation of 90 degrees clockwise, and finally a reflection across the x-axis.
What is triangle?A triangle is a polygon since it has a total of three faces along with three vertices. It belongs to the fundamental geometric shapes. Triangles having vertex positions alternating between A and B are referred to as triangles ABC. A unique plane and a triangle in Euclidean geometry appear when the three vertices are not collinear. Due to its three sides and three corners, triangles are considered polygons. The corners of a triangle are defined as the locations where its three sides meet. Three triangle angles are multiplied to get 180 degrees.
To transform triangle RST to R'S'T', we can use the following sequence of transformations:
Translation: Move the triangle 2 units to the right and 3 units down. This will result in triangle R''S''T'' with vertices (2, -3), (-2, 0), (-3, -2).
Rotation: Rotate triangle R''S''T'' 90 degrees clockwise about the origin. This will result in triangle R'''S'''T''' with vertices (3, 2), (0, 2), (2, 3).
Reflection: Reflect triangle R'''S'''T''' across the x-axis. This will result in triangle R'S'T' with vertices (3, -2), (0, -2), (2, -3).
Therefore, the sequence of transformations that produces R'S'T' from RST is translation 2 units to the right and 3 units down, followed by a rotation of 90 degrees clockwise, and finally a reflection across the x-axis.
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
In the diagram, ABC undergoes a dilation with D as the center of the dilation to create A’ B’ C’. What are possible scale factors of the dilation that will create a A’ B’ C’? Select all that apply.
Answers
The scale factor of the dilation must be greater than 1. if the image A'B'C' is bigger than the preimage ABC
What are possible scale factors of the dilationIf the image A'B'C' is bigger than the preimage ABC, then the scale factor of the dilation must be greater than 1.
In other words, the length of any segment in the image is larger than the corresponding segment in the preimage by the same factor.
Since D is the center of the dilation, we can use the ratio of the corresponding side lengths of the image and preimage triangles to find the scale factor.
For example, if we want to find the scale factor for A', we can use:
scale factor = B'C'/BC
Read more about scale factor at
https://brainly.com/question/29229124
#SPJ1
q= 2-4t/t+3
make t the subject of the formula
(please include steps!!!!) ty
Answers
Therefore (t) can be written as **(2 - 3Q) / (Q + 4)**.
Define Q?Within the given equation, Q is a variable. It stands for an unknowable amount or value that can be ascertained by equation-solving.
What exactly is variable?A quantity that can take on any one of a number of values is referred to as a variable. A variable in mathematics is a symbol or letter that denotes an unknowable amount or value. The variable Q in the given equation stands for an unknowable quantity or value that can be ascertained by resolving the equation.
The equation is as follows:
Q = (2 - 4t) / (t + 3)
When we divide both sides by (t + 3), we obtain:
Q(t + 3) = 2 - 4t
When we increase the left side of the equation, we obtain:
Qt + 3Q = 2 - 4t
The result of adding 4t to both sides of the equation is:
Qt + 3Q + 4t = 2
Combining related concepts gives us:
t(Q + 4) = 2 - 3Q
The result of dividing both sides by (Q + 4) is:
t = (2 - 3Q) / (Q + 4)
t can therefore be written as **(2 - 3Q) / (Q + 4)**.
To know more about variable visit:
brainly.com/question/29583350
#SPJ1
6²
Which theorem is shown by the diagram above?
a + b = c
C
D
a - b = c
a² + b² = c²
a²-b² = c²
Answers
The theorem is shown in a pythagoras theorem is c² = a² + b²
Which theorem is shown in a pythagoras theoremThe theorem shown in the Pythagorean theorem is "a² + b² = c²". This theorem is named after the ancient Greek mathematician Pythagoras, who is credited with discovering it.
The Pythagorean theorem applies to right-angled triangles and states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Mathematically, we can express this as:
c² = a² + b²
Where c is the length of the hypotenuse, and a and b are the lengths of the other two sides (called the legs) of the right-angled triangle.
Read more about pythagoras theorem at
https://brainly.com/question/231802
#SPJ1
Please only do 9,11, and 13! And please help!! 40 points!!!
Answers
9. The volume of the triangular pyramid is given by:
V = (1/3)Bh
Here, B is the base area.
The base is shaped as a right triangle thus, using the Pythagoras Theorem we have:
h = sqrt(26.7² - 11.7²) = 23.274 km
The area if the base is:
B = (1/2)bh = (1/2)(11.7 km)(23.4 km) = 136.89 sq. km
Now, the volume is:
V = (1/3)(136.89)(15) = 2053.35 cubic km
Hence, the volume of the triangular pyramid is 2053.35 cubic km.
9. The volume of the triangular pyramid is 2053.35 cubic km. 11. The area of the shaded portion is 348.19 cubic in 13. The slant height of the cone is 8.53 meters.
What is Pythagoras Theorem?A fundamental conclusion in geometry relating to the lengths of a right triangle's sides is known as Pythagoras' theorem. According to the theorem, the square of the length of the hypotenuse, the side that faces the right angle, in any right triangle, equals the sum of the squares of the lengths of the other two sides, known as the legs.
9. The volume of the triangular pyramid is given by:
V = (1/3)Bh
Here, B is the base area.
The base is shaped as a right triangle thus, using the Pythagoras Theorem we have:
h = √(26.7² - 11.7²) = 23.274 km
The area if the base is:
B = (1/2)bh = (1/2)(11.7 km)(23.4 km) = 136.89 sq. km
Now, the volume is:
V = (1/3)(136.89)(15) = 2053.35 cubic km
Hence, the volume of the triangular pyramid is 2053.35 cubic km.
11. The volume of a cone is given by:
V = (1/3)πr²h
The dimension of the bigger cone is radius is 9 in, and height 15 in:
V1 = (1/3)π(9 in)²(15 in) = 381.7 cubic in
The dimension of the smaller cone is radius is 4 in, and height 10 in:
V2 = (1/3)π(4 in)²(10 in) = 33.51 cubic in
Now, the area of the shaded portion is:
V1 - V2 = 381.7 - 33.51 = 348.19
13. The volume of a cone is given by:
V = (1/3)πr²h
Substituting the values we have:
542.87 = (1/3)π(6 m)²h
h = 542.87 / [(1/3)π(6 m)²] = 6.05 m
Now, using the Pythagoras Theorem for the slant height we have:
s² = r² + h²
s² = (6 m)² + (6.05 m)²
s² = 72.9
s = √(72.9) = 8.53 m
The slant height of the cone is 8.53 meters.
Learn more about Pythagoras Theorem here:
https://brainly.com/question/21926466
#SPJ1