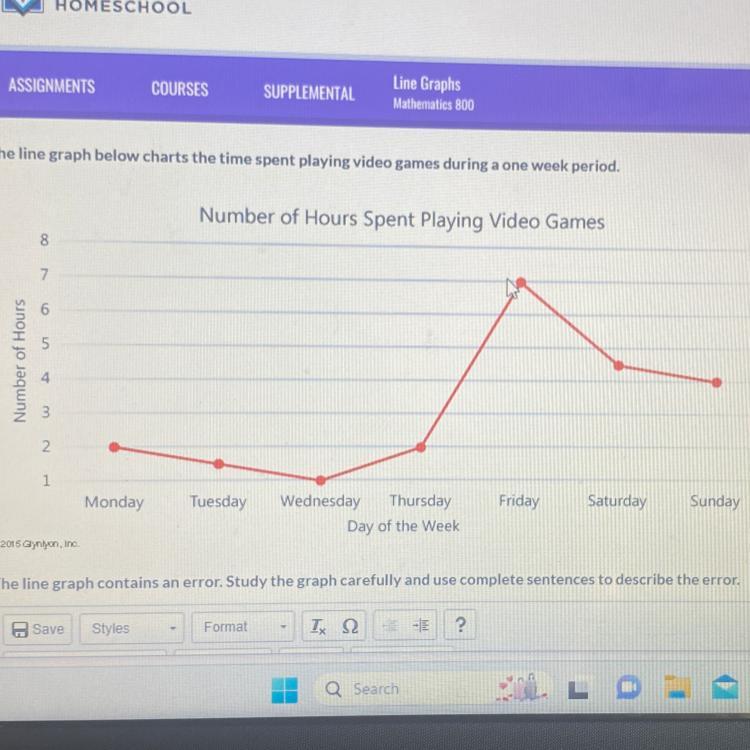
The line graph below charts the time spent playing video games during a one week period.

*LOOK AT THE PICTURE*

The line graph contains an error. Study the graph carefully and use complete sentences to describe the error.

The distance from A to B is  724.64 ft

Consider the following figure.

In right triangle CDA, the sine of angle DAC would be,

sin(∠DAC) = CD/CA

sin(32°) = CD/1540

CD = 816.1 ft

Consider the tangent of angle DAC.

tan(∠DAC ) = CD/AD

tan(32°) = 816.1 / AD

AD = 816.1/ 0.63

AD = 1295.4

Let us assume that distance AB = x feet

In right triangle CDB, the tangent of angle CBD would be,

tan(∠CBD) = CD/DB

tan(∠CBD) = CD/(DA + AB)

tan(22°) = 816.1 / (1295.4+ x)

1295.4 + x = 816.1 / 0.4040

1295.4 + x = 2020.04

x = 2020.04 -  1295.4

x = 724.64 ft

Therefore, the required distance is  724.64 ft

Learn more about the sine of angle here:

https://brainly.com/question/3827723

#SPJ4

Find the complete question below.

The expressions that correctly show the value of the electronic book device after the holiday are B and D, which represent the percentage decrease of 15% as 0.85 (or 1-0.15).

The value of an electronic book device before a holiday is represented by the variable t. After the holiday, the value of the device decreased by 15%. To find the value of the device after the holiday, we need to multiply the original value by the percentage decrease, which is 0.85 (or 1-0.15). Therefore, the expressions that correctly show the value of the electronic book device after the holiday are B and D.

Option A (1.15) represents the percentage increase and not the decrease, so it is incorrect. Option C (-0.15) represents the percentage decrease, but it cannot be used alone to find the new value. Option E (-0.85) is the negative of the percentage decrease, so it is also incorrect. Finally, option F is equivalent to option D, so it is also correct.

In summary, the expressions that correctly show the value of the electronic book device after the holiday are B and D, which represent the percentage decrease of 15% as 0.85 (or 1-0.15).

to know more about electronic

brainly.com/question/1255220

#SPJ1

Answer:

[tex]\begin{array}{|c|c|c|c|c|c|} \cline{1-6} & \text{Music} & \text{Gov} & \text{Theater} & \text{Sports} & \text{Total}\\\cline{1-6}\text{7th grade} & 42 & 12 & 20 & 58 & 132\\\cline{1-6}\text{8th grade} & 38 & 9 & 45 & 30 & 122\\\cline{1-6}\text{Total} & 80 & 21 & 65 & 88 & 254\\\cline{1-6}\end{array}[/tex]

"Gov" refers to "Student  Government".

==================================================

Explanation:

The rows are labeled "7th grade", "8th grade" and "Total".

The columns are labeled "Music", "Student  Government", "Theater", "Sports", and "Total".

I'll abbreviate "Student  Government" to "Gov" so that the table doesn't get too wide.

There are 254 students total. This value goes in the bottom right corner of the table. This is the grand total.

----------

We have 80 students in music. This value goes at the bottom of the "music" column since we're in a "total" row. Basically it's the total of all the music students regardless of grade.

Of those 80 students in music, 42 are in seventh grade. Write 42 in the first row of this column and 38 just underneath it (because 80-42 = 38). The two values 42 and 38 should add to the 80 mentioned.

----------

There are 21 students in student government. This value goes at the bottom of the "student government" column.

9 of these students are in eighth grade, so the remaining 21-9 = 12 must be in seventh grade.

----------

There are 65 students in theater. This value goes at the bottom of the "theater" column.

There are 20 such students in 7th grade and 45 in 8th grade (because 65-20 = 45).

----------

There are 88 students in sports.

30 are in 8th grade, so 88-30 = 58 must be in 7th.

----------

At this point, you should have these values along the bottom row:

80, 21, 65, 88, 254

The first four values (80, 21, 65, 88) should add to the grand total 254.

Along each row, add up the values to get the row total.

7th grade: 42 + 12 + 20 + 58 = 132

8th grade:  38 + 9 + 45 + 30 = 122

There are 132 seventh graders and 122 eighth graders.

Those subtotals add to 132+122 = 254 total students, which helps confirm we did things correctly.

The incorrect expressions are given as follows:

When two terms with the same base and different exponents are multiplied, we keep the base and add the exponents.

When two terms with the same base and different exponents are divided, we keep the base and subtract the exponents.

More can be learned about exponent rules at https://brainly.com/question/11975096

#SPJ1

The probability that a randomly selected student will be taller than 63 inches tall is 0.9332, to the nearest thousandth.

In the given triangle, α is equal to 67.36°.

What is a triangle's definition?

A triangle is a two-dimensional closed geometric form that has three sides, three angles, and three vertices (corners). It is the most basic polygon, produced by joining any three non-collinear points in a plane. The sum all angles of a triangle is always 180°. Triangles are classed according to their side length (equilateral, isosceles, or scalene) and angle measurement (acute, right, or obtuse).

Now,

Using Trigonometric functions

We can use the sine function

So,

Sin α=Perpendicular/Hypotenuse

Sin α = 12/13

α=67.36°

Hence,

           The value of α will be 67.36°.

To know more about triangles visit the link

brainly.com/question/2773823

#SPJ1

To determine the sample size needed to have a % confidence that our sample mean will be within hours of the true mean, we would need to use a formula. Specifically, we would use the formula: n = (Z^2 * s^2) / E^2

Where n is the sample size needed, Z is the z-score associated with the desired confidence level, s is the standard deviation of the population, and E is the margin of error (in this case, the specified difference of hours between the sample mean and true mean).

Assuming we have information about the population standard deviation (s), we can plug in the values for Z, s, and E to find the necessary sample size. For example, if we wanted to be 95% confident that our sample mean would be within 2 hours of the true mean, we would use a Z-score of 1.96 (which corresponds to a 95% confidence level). Let's say the population standard deviation is 5 hours. Plugging in these values, we would get:

n = (1.96^2 * 5^2) / 2^2
n = 96.04

So we would need a sample size of at least 97 in order to be 95% confident that our sample mean would be within 2 hours of the true mean.
To determine the sample size needed to be confident that our sample mean will be within a specific number of hours of the true mean, we need to know the confidence level, standard deviation, and margin of error (in hours). The formula for calculating the sample size is:

n = (Z^2 * σ^2) / E^2

where:
n = sample size
Z = Z-score corresponding to the desired confidence level
σ = population standard deviation
E = margin of error (in hours)

Once you provide the confidence level, standard deviation, and margin of error (hours), we can plug in the values and calculate the required

To learn more about  Z score- brainly.com/question/22210584

#SPJ11

x=47°

The degree of a triangle is equal to 180°.

Since a triange=180°, you would subtract 180 by 102+31 because the other two angles are 102° and 31°.

180-102-31=47°

Therefore the answer would be x=47°

The total number of ways to buy 10 pieces of fruit so that you buy at most 2 pieces with inedible cores is 137.

To determine the number of ways to buy 10 pieces of fruit so that you buy at most 2 pieces with inedible cores, we can use a combination of counting techniques.

First, we can consider the total number of ways to buy 10 pieces of fruit without any restrictions. This can be represented by the number of solutions to the equation:

x1 + x2 + x3 + x4 = 10

where x1 represents the number of bananas, x2 represents the number of apples, x3 represents the number of pears, and x4 represents the number of strawberries. Using the stars and bars method, we can find that there are C(13,3) = 286 ways to do this.

Next, we need to subtract the number of ways to buy 10 pieces of fruit where we buy 3 or more pieces with inedible cores.

We can do this by considering the number of ways to buy 3, 4, or 5 apples and pears, and then finding the number of ways to distribute the remaining pieces of fruit. Using the same method as before, we can find that there are C(12,2) + C(11,2) + C(10,2) = 221 ways to do this.

Finally, we can subtract the number of ways to buy 10 pieces of fruit where we buy 3 or more pieces with inedible cores twice, since we double-counted these cases in the previous step. Using the inclusion-exclusion principle, we can find that there are 2 * C(9,2) = 72 ways to do this.

Therefore, the total number of ways to buy 10 pieces of fruit so that you buy at most 2 pieces with inedible cores is 286 - 221 + 72 = 137.

To learn more about combination click on,

https://brainly.com/question/28213039

#SPJ4

The exponential function for the new participants is f(x) = 3 * 4^x

Let's start with the initial number of participants who sent selfies on Day 0.

We know that Aliyah, Kim, and Reese each sent selfies to 4 friends, so there are 3 x 4 = 12 participants on Day 1.

On Day 2, each of these 12 participants will send selfies to 4 friends, so we will have 12 x 4 = 48 new participants.

We can see that the number of new participants each day is increasing exponentially. In fact, the number of new participants each day is multiplied by 4, since each participant sends selfies to 4 friends.

Therefore, we can write an exponential function of the form:

f(x)=a * 4^x

Where x is the number of days since the challenge started, and $a$ is the initial number of participants who sent selfies on Day 0.

We know that a = 12 from our earlier calculations.

So, we have

f(x) = 3 * 4^x

Hence, the function is f(x) = 3 * 4^x

Read more about exponential function at

https://brainly.com/question/2456547

#SPJ1

The actual height of the statue is option C 231.2 feet.

A scale factor is a number used in mathematics to scale or multiply a quantity or measurement by another factor in order to establish a proportional relationship between two identical figures or objects.

In other terms, the scale factor is the ratio of the corresponding lengths, widths, or heights of the two figures or objects if they are similar, that is, they have the same shape but may range in size. This implies that you may determine the dimension of the second object by multiplying one dimension of one object by the scale factor.

Given that the scale factor is 230:1.

Thus,

actual height of statue / 230 = height of drawing / 1.2 feet

Now,

actual height of statue = (1.2 feet / 1.2 feet) * 230

actual height of statue = 230 feet

Hence, the actual height of the statue is option C 231.2 feet.

Learn more about scale factor here:

https://brainly.com/question/29464385

#SPJ1

Answer: Beth and Jose should leave a $6.15 tip.

Step-by-step explanation: We need to find 20% of $30.75 so you need to multiply 30.75 by 0.20 to find 6.15 to be 20% of 30.75.

Answer:

A) $6.15

Step-by-step explanation:

20%= 0.2
30.75 x 0.2 = 6.15

The power series method can be used to solve a nonhomogeneous differential equation about an ordinary point by finding both a homogeneous and particular solution using a series expansion and the method of undetermined coefficients.

The power series method is a technique used to find a series solution of a differential equation. When applied to a nonhomogeneous differential equation, the method involves finding both a homogeneous solution and a particular solution.

Assuming that the nonhomogeneous differential equation has the form

y''(x) + p(x)y'(x) + q(x)y(x) = f(x)

where p(x), q(x), and f(x) are functions of x, we can begin by finding the solution to the associated homogeneous equation

y''(x) + p(x)y'(x) + q(x)y(x) = 0

Using the power series method, we can assume a solution of the form:

y(x) = a0 + a1(x - x0) + a2(x - x0)^2 + ...

where a0, a1, a2, ... are constants to be determined, and x0 is the ordinary point of the differential equation.

Next, we can find the coefficients of the power series by substituting the series solution into the differential equation and equating coefficients of like powers of (x-x0). This leads to a system of equations for the coefficients, which can be solved iteratively.

After finding the homogeneous solution, we can find a particular solution using a similar method. Assuming a particular solution of the form:

y(x) = u(x) + v(x)

where u(x) is a solution to the associated homogeneous equation, and v(x) is a particular solution to the nonhomogeneous equation, we can use the method of undetermined coefficients to find v(x). This involves assuming a form for v(x) based on the form of f(x), and then solving for its coefficients using the same technique as before.

Once we have found both the homogeneous and particular solutions, we can combine them to obtain the general solution to the nonhomogeneous differential equation.

Learn more about nonhomogeneous differential equation here

brainly.com/question/30876746

#SPJ4

So the transformation is: (x, y) → (x + -8, y - 4) which is equivalent to option B.

In mathematics, a transformation is a process that manipulates the position, size, or shape of a geometric object. Transformations can include translations, rotations, reflections, and dilations. They are used to study geometric properties and relationships and are often used in fields such as geometry, algebra, and computer graphics. Transformations are important in understanding symmetry and congruence, as well as in solving problems involving geometric figures.

Here,

We can see that the transformation takes each point of the form (x, y) in ABC to a corresponding point of the form (x', y') in A'B'C'. To find the correct transformation, we need to determine how the coordinates of the points in ABC are related to the coordinates of the corresponding points in A'B'C'. One way to do this is to use the fact that the transformation should preserve the relative distances and angles between the points. Another way is to use the known coordinates of three corresponding points to determine the transformation directly.

In this case, we can see that the transformation maps (-3,-2) to (5,2), (-1,-4) to (7,0), and (-6,-5) to (2,-1). We can use these points to find the transformation:

(x, y) → (x', y')

To map (-3,-2) to (5,2), we need to add 8 to the x-coordinate and add 4 to the y-coordinate:

x' = x + 8

y' = y + 4

To map (-1,-4) to (7,0), we again add 8 to the x-coordinate, but this time we only add 4 to the y-coordinate:

x' = x + 8

y' = y + 4

To map (-6,-5) to (2,-1), we subtract 4 from the x-coordinate and subtract 4 from the y-coordinate:

x' = x - 4

y' = y - 4

To know more about transformation,

https://brainly.com/question/29641135

#SPJ1

The probability of the weekend being dry for the school picnic is approximately 23.4%.

First, let's define some terms:

1. Probability: The likelihood of a specific event happening
2. Picnic: The school event that is scheduled for a two-day weekend in May
3. Rainy: Refers to days with rain

Now, let's calculate the probability that the weekend will be dry:

There are 16 rainy days in May, and May has 31 days. So, there are (31 - 16) = 15 dry days in May.

Each weekend has two days. Since May has 31 days, there are (31 / 7) = approximately 4.43 weeks in May. To account for the remaining days, we round down to 4 weeks and add the remaining 2 days as another weekend, resulting in 5 weekends.

Now, we'll determine the probability of having a dry day on any given day in May:

Dry day probability = (number of dry days) / (total days in May) = 15 / 31 ≈ 0.484

Since we want the probability of having two consecutive dry days (the whole weekend), we'll multiply the probabilities of each day being dry:

Weekend probability of being dry = (dry day probability) * (dry day probability) ≈ 0.484 * 0.484 ≈ 0.234

So, the probability of the weekend being dry for the school picnic is approximately 23.4%.

Learn more about Probability here: brainly.com/question/30034780

#SPJ11

The range for the data set is equal to 48.

In Mathematics and Statistics, a range is the difference between the highest number and the lowest number contained in a data set.

In Mathematics and Statistics, the range of a data set can be calculated by using this mathematical expression;

Range = Highest number - Lowest number

From the given data set, we have:

Highest number = 95.

Lowest number = 47.

By substituting, we have:

Range = 95 - 47

Range = 48.

Read more on range here: brainly.com/question/32352196

#SPJ2

the equation of the ellipse with center at the origin, a vertex at (0, 6), and a co-vertex at (2, 0) is:(x² / 36) + (y² / 4) = 1

How to solve the question?

To write the equation of an ellipse in standard form when the center is at the origin, we need to use the following formula:

(x²/ a²) + (y² / b²) = 1

where a is the distance from the center to a vertex, and b is the distance from the center to a co-vertex.

In our problem, the center is at the origin, and a vertex is located at (0, 6), so the distance from the center to a vertex is 6. Therefore, we have:

a = 6

Similarly, a co-vertex is located at (2, 0), so the distance from the center to a co-vertex is 2. Therefore, we have:

b = 2

Substituting these values into the formula above, we get:

(x² / 6²) + (y² / 2²) = 1

Simplifying, we get:

(x² / 36) + (y² / 4) = 1

Therefore, the equation of the ellipse with center at the origin, a vertex at (0, 6), and a co-vertex at (2, 0) is:

(x² / 36) + (y² / 4) = 1

This is the equation in standard form for an ellipse with a horizontal major axis (since a is greater than b), and it represents an ellipse that is taller than it is wide. The major axis of the ellipse is the line passing through the vertices, which in this case is the y-axis, and the minor axis is the line passing through the co-vertices, which in this case is the x-axis.

To know more about vertex visit :-

https://brainly.com/question/29476657

#SPJ1

Step-by-step explanation:

7 + x = 2x, so x = 7

The substance's half-life in days is 3 days.

What is exponential decay?

If a quantity declines at a pace proportionate to its current value, exponential decay may be present. The term "exponential decay" in mathematics refers to the process of a constant percentage rate reduction in an amount over time.

Here, we have

Given: An 18-gram sample of a substance that's a by-product of fireworks has a k-value of 0.215.

We have to find the substance's half-life in days.

Using the formula for the exponential decay that is N = N₀e⁻ⁿˣ,

we have N = 18/2, N₀ = 18, and n = 0.215.

N = N₀e⁻ⁿˣ

9 = 18e⁻⁰°²¹⁵ˣ

9/18 = e⁻⁰°²¹⁵ˣ

1/2 = e⁻⁰°²¹⁵ˣ

Taking logs on both sides, we get

㏑(1/2) = -0.215x

x = ㏑(1/2)/(-0.215)

x = -0.6931/(-0.215)

x = 3.22

Hence, the substance's half-life in days is 3 days.

To learn more about the exponential decay from the given link

https://brainly.com/question/31409569

#SPJ1

The explicit formula for an arithmetic sequence is:

an = a1 + (n-1)d

The explicit formula for a geometric sequence is:

an = a1 * [tex]r^{(n-1)}[/tex]

What is arithmetic sequence?

An arithmetic sequence is a sequence of numbers in which each term after the first is found by adding a fixed constant number, called the common difference, to the preceding term.

To write the explicit formula for both an arithmetic and geometric sequence, the following values must be known:

For an Arithmetic Sequence:

The first term (a1) of the sequence.

The common difference (d) between consecutive terms in the sequence.

The explicit formula for an arithmetic sequence is:

an = a1 + (n-1)d

Where:

an is the nth term of the sequence.

a1 is the first term of the sequence.

d is the common difference between consecutive terms.

n is the position of the term in the sequence.

For a Geometric Sequence:

The first term (a1) of the sequence.

The common ratio (r) between consecutive terms in the sequence.

The explicit formula for a geometric sequence is:

an = a1 * r^(n-1)

Where:

an is the nth term of the sequence.

a1 is the first term of the sequence.

r is the common ratio between consecutive terms.

n is the position of the term in the sequence.

Therefore, The explicit formula for an arithmetic sequence is:

an = a1 + (n-1)d

The explicit formula for a geometric sequence is:

an = a1 * [tex]r^{(n-1)}[/tex]

To learn more about arithmetic sequence from the given link:

https://brainly.com/question/15412619

#SPJ1

The given statement about developing quantitative and measurable usability tests is true.

Use cases can help with developing quantitative and measurable usability tests. Use cases are scenarios that describe how a user might interact with a system or product in a specific situation.

By developing use cases, researchers can identify specific tasks that users may need to perform and design usability tests to measure how well users can perform those tasks.

This can help make the usability tests more objective and measurable, as researchers can use metrics such as completion rates, task time, and errors to assess the usability of the system or product.

Learn more about usability tests.

brainly.com/question/28807738

#SPJ11

Using the substitution method we know that the value of y in the given situation is 2 respectively.

The substitution method is typically used in mathematics to solve an equation system.

In this approach, you solve the equation for one variable first, then you enter its value into the other equation.

A false statement is produced if the variables x = 3 and y = 2 are substituted into the first equation: 2(2) = 3 + 9.

Try changing the first equation as x = 2y 8 to solve this system.

Next, change x in the second equation to 2y 8, and then solve for y.

The right response is x = 2, y = 3.

So, get the value of y as follows:

3x - 9y =8 ...(1)

-2x + 2y= 8 ...(2)

Now, take equation (1):

3x - 9y =8

3x = 8 + 9y

x = (8 + 9y)/3

Now, substitute x = (8 + 9y)/3 in equation (2):

-2x + 2y= 8

-2[(8 + 9y)/3] + 2y= 8
-2[(8 + 9y)] + 2y= 8*3
-16 + 18y + 2y = 24

20y = 24 + 16

20y = 40

y = 40/20

y = 2

Therefore, using the substitution method we know that the value of y in the given situation is 2 respectively.

Know more about the substitution method here:

https://brainly.com/question/22340165

#SPJ1

The range of f include the following: D. -5 ≤ f(x) ≤ 5.

In Mathematics and Geometry, a domain is the set of all real numbers for which a particular function is defined.

Additionally, the vertical extent of any graph of a function represents all range values and they are always read and written from smaller to larger numerical values, and from the bottom of the graph to the top.

By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:

Domain = {-6, 5} or -6 ≤ x ≤ 5.

Range = {-5, 5} or -5 ≤ f(x) ≤ 5.

Read more on domain here: brainly.com/question/17440903

#SPJ1

Answer:1

1. is 2/7

2. is .5

3 is 1.94 repeating and

4 is 7/11

Step-by-step explanation:

To find the mean height of a football player on this Florida team, we need to know the mean of the normal distribution (Morlam) and the standard deviation of the Florida distribution. Since the Florida distribution is also approximately normal (Morlam) with a standard deviation of 2.9 inches, we can use the Empirical Rule to estimate the mean height.

According to the Empirical Rule, approximately 68% of the data falls within one standard deviation of the mean, approximately 95% within two standard deviations, and approximately 99.7% within three standard deviations. Since we know that the standard deviation of the Florida distribution is 2.9 inches, we can assume that the mean height falls within three standard deviations of the mean.

So, if we assume that the mean height is at the centre of the distribution, we can estimate it by adding and subtracting three standard deviations from it. Therefore, the mean height of a football player on this Florida team can be estimated to be:

Mean height = Mean of the Morlam distribution ± 3 x Standard deviation of the Florida distribution
Mean height = Mean of the Morlam distribution ± 3 x 2.9 inches

Without knowing the mean of the Morlam distribution, we cannot calculate the exact mean height. However, if we assume that the Morlam distribution has a mean height of 70 inches (a typical average height for a football player), then the mean height of a football player on this Florida team can be estimated to be:

Mean height = 70 ± 3 x 2.9
Mean height = 70 ± 8.7
Mean height = 61.3 to 78.7 inches

Therefore, we can estimate that the mean height of a football player on this Florida team is between 61.3 and 78.7 inches.

Learn more about Normal Distribution here: brainly.com/question/17199694

#SPJ11

We can estimate that the mean height of a football player on the Florida team is approximately 70 inches.

To find the mean height of a football player on the Florida team, we need to know the exact distribution of heights. However, since we only have information about the standard deviation and the fact that it is approximately normal, we can make an educated guess that the distribution is still normal with a mean somewhere close to the national average of 70 inches.
Using the empirical rule, we know that about 68% of the data falls within one standard deviation of the mean. In this case, one standard deviation is 2.9 inches.

So, we can assume that about 68% of the heights on the Florida team fall between (70-2.9) = 67.1 inches and (70+2.9) = 72.9 inches.
If we assume that the distribution is symmetric, we can estimate the mean height of the Florida team by taking the average of the lower and upper bounds of the interval: (67.1 + 72.9)/2 = 70 inches.

For similar question on mean.

https://brainly.com/question/23251787

#SPJ11

Answer:

6.8 ounces

To set up a hypothesis test for this production process, we need to define the null and alternative hypotheses. The null hypothesis (H0) is that the average amount of soda in each can is equal to 6.8 ounces, while the alternative hypothesis (Ha) is that the average amount of soda in each can is not equal to 6.8 ounces.

We can then collect data by taking regular random samples from the production process and calculate the sample mean and standard deviation. We can then perform a statistical test such as a t-test or z-test to determine whether we can reject or fail to reject the null hypothesis.

If we reject the null hypothesis, we can conclude that there is evidence that the average amount of soda in each can is different from 6.8 ounces. If we fail to reject the null hypothesis, we cannot conclude that there is evidence that the average amount of soda in each can is different from 6.8 ounces.

I hope this helps! Let me know if you have any other questions.

When we look across each row of the table the pattern we observe is that the multiplication of the table leads to 12.

The quantity of space a three-dimensional item occupies is measured by its volume. Usually, it is expressed in cubic units like cubic metres or cubic feet. If an object has irregular or curved shapes, the volume can be determined by using its measurements, such as length, breadth, and height, or by employing more difficult mathematical calculations. In several disciplines, such as physics, engineering, and architecture, volume is a crucial notion.

From the table we see that the arrangement of the 12 cubes is made in different length and width, such that the multiplication of the three is 12.

Here we have,

Long    wide       tall

2            3             2

2             6            1

3             1             4

3             2            2

3             4            1

4              1            3

6              2            1

Hence, when we look across each row of the table the pattern we observe is that the multiplication of the table leads to 12.

Learn more about volume here:

https://brainly.com/question/1578538

#SPJ1

The complete question is:

The position of the image is approximately 1.71 cm from the ornament's surface.

To determine the position of the image, we need to use the mirror formula for a concave mirror, which is \frac{1}{f} = [tex]\frac{1}{do} + \frac{1}{di},[/tex] where f is the focal length, do is the object distance, and di is the image distance.

First, we need to find the focal length (f) of the spherical ornament. The radius of curvature (R) is half the diameter, so R = 6.00 cm / 2 = 3.00 cm. For a spherical mirror, the focal length is half the radius of curvature: f = R/2 = 3.00 cm / 2 = 1.50 cm.

Next, we need to find the object distance (do). The object is 19.0 cm from the center of the ornament, but we need the distance from the ornament's surface. Since the radius is 3.00 cm, we subtract that from the total distance: do = 19.0 cm - 3.00 cm = 16.0 cm.

Now, we can use the mirror formula:
\frac{1}{f} = [tex]\frac{1}{do} + \frac{1}{di},[/tex]
1/1.50 cm = 1/16.0 cm + 1/di

To solve for di, subtract 1/16.0 cm from both sides and then take the reciprocal:

1/di = 1/1.50 cm - 1/16.0 cm

di ≈ 1.71 cm

The position of the image is approximately 1.71 cm from the ornament's surface.

learn more about the mirror formula for a concave mirror,

https://brainly.com/question/3555871

#SPJ11

The position of the image is 20.8 cm from the center of the spherical ornament, counting from the ornament surface.

To find the position of the image, we can use the mirror equation:

1/o + 1/i = 1/f

where o is the object distance from the center of the spherical ornament, i is the image distance from the center of the spherical ornament, and f is the focal length of the ornament.

Since the ornament is a spherical mirror, the focal length is half the

radius of curvature, which is half the diameter of the ornament:

f = R/2 = 6.00 cm/2 = 3.00 cm

Substituting the given values, we get:

1/19.0 cm + 1/i = 1/3.00 cm

Solving for i, we get:

1/i = 1/3.00 cm - 1/19.0 cm = (19.0 cm - 3.00 cm)/(3.00 cm x 19.0 cm) = 0.0481 cm^-1

i = 1/0.0481 cm = 20.8 cm

Therefore, the position of the image is 20.8 cm from the center of the

spherical ornament, counting from the ornament surface.

for such more question on ornament surface

https://brainly.com/question/30938695

#SPJ11