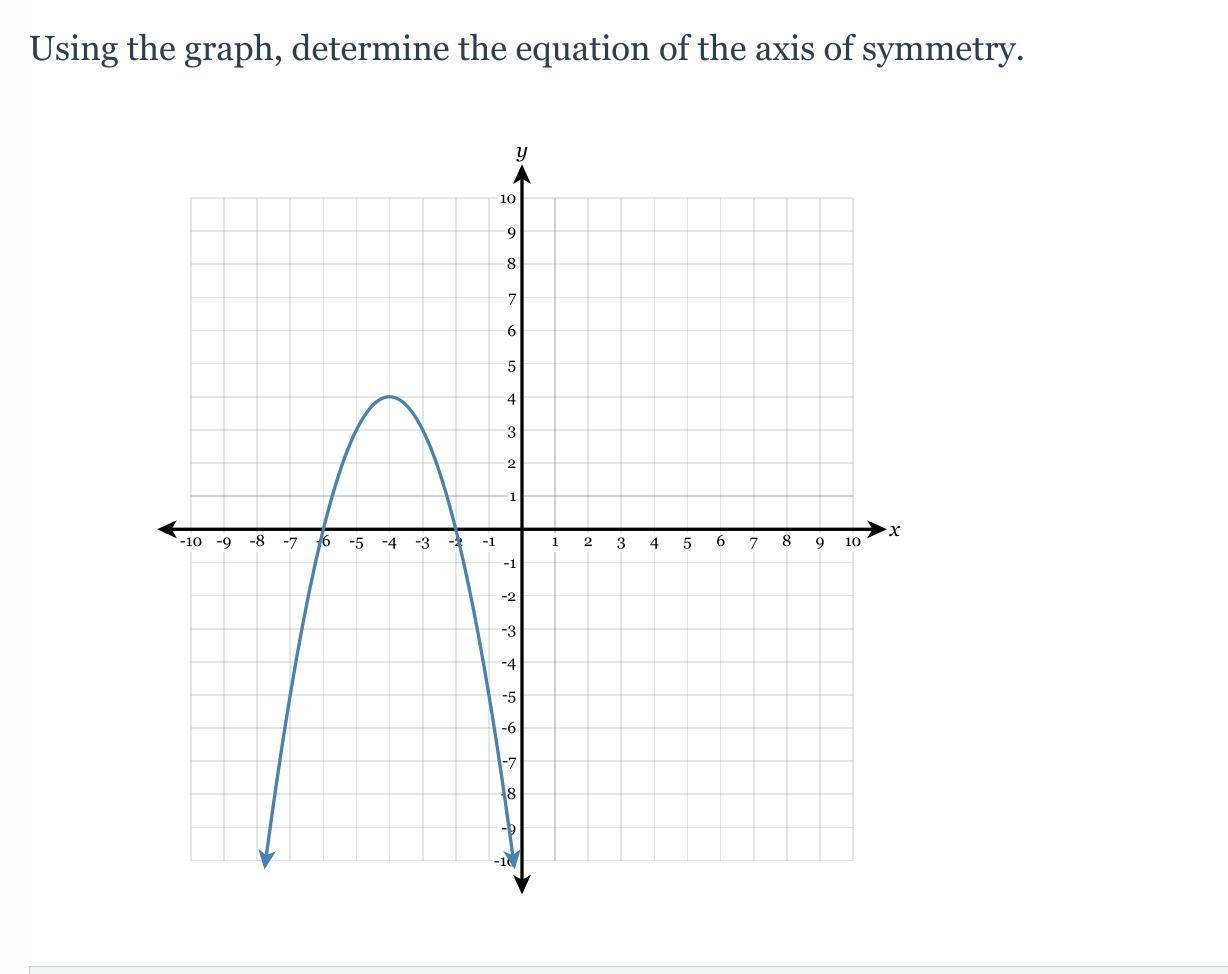
Answers
Step-by-step explanation:
x = -4 ( the value of the x-coordinate of the vertex is the axis of symmetry for normal up or down opening parabolas)
Related Questions
What is the remainder? Equation is below.
Answers
Answer:
-23. In my explanation I will include in my picture how this will look in your final answer
Step-by-step explanation:
So to solve this, I first set x + 3 = 0. This means that x = -3, which we will use soon. Now, here's how you would work out this problem. It would be confusing if I explained over text, so I included a picture of my work.
You would first set up your problem like it is in the picture. Then, bring 2 down. Next, multiply 2 by -3 (for future problems, you would multiply the number you brought down by whatever number is on the side). -3 × 2 = -6, so you would put that under 3 (as shown in the picture). Now, add 3 and -6 (which = -3). Repeat this step each time.
I hope this made sense! Please let me know if you have any questions.
in a(n) , the scale questions are divided into two parts equally and the resulting scores of both parts are correlated against one another.
Answers
The main topic is the split-half reliability test used in psychological research to assess the internal consistency of a scale.
How to test the psychological research?In psychological research, reliability is a crucial aspect of measuring constructs or attributes. One commonly used method for assessing the reliability of a scale is the split-half reliability test.
In this test, the scale questions are divided into two parts equally, and the resulting scores of both parts are correlated against one another.
For example, if a scale had 20 items, the items could be randomly split into two groups of 10 items each.
Scores are then calculated for each group, and the scores are correlated with each other to determine the degree of consistency between the two halves.
The correlation coefficient obtained from this analysis provides an estimate of the internal consistency of the scale.
A high correlation coefficient indicates a high level of internal consistency, indicating that the two halves of the scale are measuring the same construct or attribute.
Conversely, a low correlation coefficient suggests that the two halves of the scale are not measuring the same construct or attribute, and the scale may need to be revised or abandoned.
Overall, the split-half reliability test provides a quick and efficient method for evaluating the reliability of a scale.
However, it is important to note that this method does have some limitations, such as the possibility of unequal difficulty or discrimination of the items in each half of the scale.
Therefore, researchers often use other methods, such as Cronbach's alpha, in conjunction with the split-half reliability test to provide a more comprehensive assessment of the reliability of a scale
Learn more about reliability test
brainly.com/question/27873337
#SPJ11
which of the following null hypothesis statistical tests require calculating degrees of freedom? group of answer choices all of the above two-sample t-test chi-squared one-sample t-test
Answers
The two null hypothesis that are correct answer are two-sample t-test and one-sample t-test.
Among the group of answer choices provided, the tests that require calculating degrees of freedom are the two-sample t-test and the one-sample t-test. Both of these tests belong to the t-test family and involve using degrees of freedom to determine the critical t-value.
In summary:
- Null hypothesis: The assumption that there is no significant difference between the sample and population or between two samples.
- T-test: A statistical test used to determine if there is a significant difference between the means of two groups or between a sample and population mean.
- Degrees of freedom: A value used in statistical tests that represents the number of independent values in a data set, which can affect the outcome of the test.
So answer is: two-sample t-test and one-sample t-test.
Learn more about null hypothesis here:
https://brainly.com/question/28920252
#SPJ11
The null hypothesis statistical tests that require calculating degrees of freedom are the two-sample t-test and the one-
sample t-test. The degrees of freedom are necessary to calculate the t-value for these tests. The chi-squared test also
requires degrees of freedom, but it is not a test for a null hypothesis.
The correct answer is: all of the above.
All these tests require calculating degrees of freedom:
1. Two-sample t-test:
Degrees of freedom are calculated using the formula (n1 + n2) - 2, where n1 and n2 are the sample sizes of the two
groups being compared.
2. Chi-squared test:
Degrees of freedom are calculated using the formula (rows - 1) * (columns - 1), where rows and columns represent the
number of categories in the data.
3. One-sample t-test:
Degrees of freedom are calculated using the formula n - 1, where n is the sample size.
The null hypothesis statistical tests that require calculating degrees of freedom are the two-sample t-test and the one-
sample t-test. The degrees of freedom are necessary to calculate the t-value for these tests. The chi-squared test also
requires degrees of freedom, but it is not a test for a null hypothesis.
for such more question on null hypothesis
https://brainly.com/question/4436370
#SPJ11
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups. She writes the equation r = 2/5 to describe the relationship.
Answers
In the given equation r = 2/5 t "r" is the dependent variable.
Dependent variables:In mathematics, a variable is a symbol that represents a quantity that can take on different values. In many cases, variables can be divided into two types: dependent variables and independent variables.
An independent variable is a variable that can be changed freely, and its value is not dependent on any other variable in the equation.
A dependent variable is a variable whose value depends on the value of one or more other variables in the equation
Here we have
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups.
She writes the equation r = 2/5 t to describe the relationship.
In the equation, r = 2/5 t, "t" represents the total number of cups, while "r" represents the number of cups of red paint.
Here "t" is the independent variable because it represents the total number of cups, which can be changed arbitrarily.
The value of "r" depends on the value of "t" because the number of cups of red paint is always 2/5 of the total number of cups.
Therefore,
In the given equation r = 2/5 t "r" is the dependent variable.
Learn more about Variables at
https://brainly.com/question/1479694
#SPJ1
Complete Question:
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups. She writes the equation r = 2/5 t to describe the relationship. Which is the independent variable? Which is the dependent variable? Explain how you know.
A triangle has two legs measuring 21 cm and 20 cm. Which of the following leg measurement will make a right triangle?
Answers
The leg measurement will make a right triangle is 21 cm.
What is hypotenous?The longest side of a right-angled triangle, i.e. the side opposite the right angle, is called the hypotenuse in geometry.
Pythagorean theorem :
If p be the length of the hypotenuse of a right-angled triangle, q and r be the lengths of the other two sides, then
p² = q² + r²
The lengths of the other two sides of the given right-angled triangle are 20 cm and 21 cm. Put these values in the above theorem to get the desired result.
Now, p² = (20)² + (21)²
= 400 + 441 = 841
i.e. p = √(841) = 29
Therefore the length of the hypotenuse is 29 cm. The right angle traingle is 21 cm.
Learn more about hypotenuse, here:
https://brainly.com/question/28946097
#SPJ1
need answer by 11:45am
The box plots display measures from data collected when 20 people were asked about their wait time at a drive-thru restaurant window.
A horizontal line starting at 0, with tick marks every one-half unit up to 32. The line is labeled Wait Time In Minutes. The box extends from 8.5 to 15.5 on the number line. A line in the box is at 12. The lines outside the box end at 3 and 27. The graph is titled Super Fast Food.
A horizontal line starting at 0, with tick marks every one-half unit up to 32. The line is labeled Wait Time In Minutes. The box extends from 9.5 to 24 on the number line. A line in the box is at 15.5. The lines outside the box end at 2 and 30. The graph is titled Burger Quick.
Which drive-thru typically has more wait time, and why?
Burger Quick, because it has a larger median
Burger Quick, because it has a larger mean
Super Fast Food, because it has a larger median
Super Fast Food, because it has a larger mean
Question 3
A charity needs to report its typical donations received. The following is a list of the donations from one week. A histogram is provided to display the data.
5, 5, 6, 8, 10, 15, 18, 20, 20, 20, 20, 20, 20
A graph titled Donations to Charity in Dollars. The x-axis is labeled 1 to 5, 6 to 10, 11 to 15, and 16 to 20. The y-axis is labeled Frequency. There is a shaded bar up to 2 above 1 to 5, up to 3 above 6 to 10, up to 1 above 11 to 15, and up to 7 above 16 to 20.
Which measure of variability should the charity use to accurately represent the data? Explain your answer.
The range of 13 is the most accurate to use, since the data is skewed.
The IQR of 13 is the most accurate to use, since the data is skewed.
The range of 20 is the most accurate to use to show that they have plenty of money.
The IQR of 20 is the most accurate to use to show that they need more money.
Question 4
The circle graph describes the distribution of preferred transportation methods from a sample of 400 randomly selected San Francisco residents.
circle graph titled San Francisco Residents' Transportation with five sections labeled walk 40 percent, bicycle 8 percent, streetcar 15 percent, bus 10 percent, and cable car 27 percent
Which of the following conclusions can we draw from the circle graph?
Together, Streetcar and Cable Car are the preferred transportation for 168 residents.
Together, Walk and Streetcar are the preferred transportation for 55 residents.
Bus is the preferred transportation for 45 residents.
Bicycle is the preferred transportation for 50 residents.
Question 5
The line plot displays the number of roses purchased per day at a grocery store.
A horizontal line starting at 1 with tick marks every one unit up to 10. The line is labeled Number of Rose Bouquets, and the graph is titled Roses Purchased Per Day. There is one dot above 1 and 2. There are two dots above 8. There are three dots above 6, 7, and 9.
Which of the following is the best measure of variability for the data, and what is its value?
The range is the best measure of variability, and it equals 8.
The range is the best measure of variability, and it equals 2.5.
The IQR is the best measure of variability, and it equals 8.
The IQR is the best measure of variability, and it equals 2.5.
Question 6
The histograms display the frequency of temperatures in two different locations in a 30-day period.
A graph with the x-axis labeled Temperature in Degrees, with intervals 60 to 69, 70 to 79, 80 to 89, 90 to 99, 100 to 109, 110 to 119. The y-axis is labeled Frequency and begins at 0 with tick marks every one unit up to 14. A shaded bar stops at 10 above 60 to 69, at 9 above 70 to 79, at 5 above 80 to 89, at 4 above 90 to 99, and at 2 above 100 to 109. There is no shaded bar above 110 to 119. The graph is titled Temps in Sunny Town.
A graph with the x-axis labeled Temperature in Degrees, with intervals 60 to 69, 70 to 79, 80 to 89, 90 to 99, 100 to 109, 110 to 119. The y-axis is labeled Frequency and begins at 0 with tick marks every one unit up to 16. A shaded bar stops at 2 above 60 to 69, at 4 above 70 to 79, at 12 above 80 to 89, at 6 above 90 to 99, at 4 above 100 to 109, and at 2 above 110 to 119. The graph is titled Temps in Desert Landing.
When comparing the data, which measure of center should be used to determine which location typically has the cooler temperature?
Median, because Desert Landing is symmetric
Mean, because Sunny Town is skewed
Mean, because Desert Landing is symmetric
Median, because Sunny Town is skewed
Question 7
At a recent baseball game of 5,000 in attendance, 150 people were asked what they prefer on a hot dog. The results are shown.
Ketchup Mustard Chili
63 27 60
Based on the data in this sample, how many of the people in attendance would prefer mustard on a hot dog?
900
2,000
2,100
4,000
Answers
The drive-thru with typically more wait time is Burger Quick, because it has a larger median. The Option A.
Why does Burger Quick have a larger median for wait time?The median is a measure of central tendency that represents the middle value of a set of data. In this case, the median wait time at Burger Quick is 15.5 minutes, while the median wait time at Super Fast Food is 12 minutes.
This indicates that, on average, customers at Burger Quick experience a longer wait time compared to customers at Super Fast Food. The larger median at Burger Quick suggests that there may be some longer wait times skewing the data towards the higher end which could be due to various factors such as slower service, or other operational issues at Burger Quick resulting in a longer wait time for customers at their drive-thru.
Read more about median
brainly.com/question/16408033
#SPJ1
fractions to decimals
Answers
Answer: 1 is .4
2. is .6
3 is .5
4 is .375
5 is .18
6 is .71
7 is .16
8 is .66 repeating
9 is .91
and 10 is .25
Step-by-step explanation:
to get all these and fractions to decimals in the future just divide the numerator by the denominator in other words the top number by the bottom number
1): 0.4
2): 0.67 or 0.7
3): 0.5
4): 0.37 or 0.4
5): 0.18
6): 0.42 or 0.5
7): 0.17
8): 0.7
9): 0.97 or 1
10): 0.25
A helicopter hovering above a command post shines a spotlight on an object on the ground 250 feet away from the command post as shown in the diagram how far is the object from the helicopter to the nearest foot
Answers
The distance of the object from the helicopter is 698 ft.
What is distance?Distance is the length between two points.
To calculate how far the object is above the helicopter, we use the formula below.
Formula:
Sin∅ = O/H..................... Equation 1Where:
∅ = AngleO = OppositeH = Hypotenus = Distance of the object from the HelicopterFrom the question,
Given:
O = 250 ft∅ = 21°Substitute these values into equation 1 and solve for H
H = 250/Sin21°H = 697.61 ftH ≈ 698 ftHence, the distance is 698 ft.
Learn more about distance here: https://brainly.com/question/26046491
#SPJ1
Find the value of x .
J
30°
M
to
K
(2x - 30)°
[
Answers
The value of x in the Intersecting chords is 15
Finding the value of x .From the question, we have the following parameters that can be used in our computation:
Intersecting chords
The value of x is then calculated as
x = 1/2(30 - 2x + 30)
So, we have
2x = 30 - 2x + 30
Evaluate the like terms
4x = 60
Divide
x = 15
Hence, the value of x is 15
Read more about angles at
https://brainly.com/question/28293784
#SPJ1
For the function 8-(x-3)^2,
state the domain
Answers
The domain of the function 8 - [tex](x-3)^{2}[/tex] is R which is all the real numbers.
What is domain of a function?
The set or grouping of all potential values that may be used in the function is known as the domain.
We are given a function as 8 - [tex](x-3)^{2}[/tex].
Now, in order to find the domain, we need to find the values where the function is not defined for a value of x.
But, there is no such value for x where the function is not defined.
This means that all values of x give an output.
So, the domain is the set of all the real numbers.
Hence, the domain of the given function is R.
Learn more about domain of function from the given link:
https://brainly.com/question/1369616
#SPJ1
A=P(1+r/n)^nt Find how long it takes for $1400 to double if it is invested at 7% interest compounded monthly. Use the formula A = P to solve the compound interest problem. TE The money will double in value in approximately years. (Do not round until the final answer. Then round to the nearest tenth as needed.)
Answers
It will take 10 years to double the amount.
Given that, the amount $1400 to double if it is invested at 7% interest compounded monthly, we need to calculate the time,
[tex]A = P(1+r/n)^{nt}[/tex]
[tex]2800 = 1400(1+0.0058)^{12t}[/tex]
[tex]2= (1.0058)^{12t[/tex]
㏒ 2 = 12t ㏒ (1.0058)
0.03 = 12t (0.0025)
12t = 120
t = 10
Hence, it will take 10 years to double the amount.
Learn more about compound interest click;
https://brainly.com/question/14295570
#SPJ1
a kite flying in the air has a 94- string attached to it, and the string is pulled taut. the angle of elevation of the kite is . find the height of the kite. round your answer to the nearest tenth.
Answers
The height of the kite is approximately 68.4 ft.
To solve the problem, we can use trigonometry. We know that the string is the hypotenuse of a right triangle, with the height of the kite as one of the legs. The angle of elevation, which is the angle between the string and the ground, is also given. We can use the tangent function to find the height of the kite:
tan(46°) = height / 94
Solving for height, we get:
height = 94 * tan(46°)
Using a calculator, we get:
height ≈ 68.4 ft
Therefore, the height of the kite is approximately 68.4 ft.
We use the given angle of elevation and the length of the string to set up a right triangle with the height of the kite as one of the legs. Then, we use the tangent function to relate the angle to the height of the kite. Finally, we solve for the height using a calculator and round to the nearest tenth as requested.
Learn more about the height
https://brainly.com/question/28122539
#SPJ4
Complete Question:
A kite flying in the air has a 94-ft string attached to it, and the string is pulled taut. The angle of elevation of the kite is 46 °. Find the height of the kite. Round your answer to the nearest tenth.
call a positive integer kinda-prime if it has a prime number of positive integer divisors. if there are $168$ prime numbers less than $1000$, how many kinda-prime positive integers are there less than $1000$?
Answers
There are 173 kinda-prime positive integer less than 1000.
To find the number of kinda-prime positive integer less than 1000, we'll follow these steps:
1. Understand the definition of a kinda-prime number: A positive integer is kinda-prime if it has a prime number of positive integer divisors.
2. Determine the number of prime numbers less than 1000: There are 168 prime numbers less than 1000, as given.
3. Determine the possible prime number of divisors: Since 168 is not too large, we only need to consider 2 and 3 as possible prime numbers of divisors for a kinda-prime number.
4. Analyze the cases:
Case 1: Kinda-prime numbers with 2 divisors (prime numbers)
All prime numbers have exactly 2 divisors (1 and itself). Thus, all 168 prime numbers less than 1000 are kinda-prime.
Case 2: Kinda-prime numbers with 3 divisors
Let N be a kinda-prime number with 3 divisors. Then, N = p^2 for some prime number p. To find the suitable prime numbers p, we need[tex]p^2 < 1000[/tex]. The prime numbers that meet this condition are 2, 3, 5, 7, and 11 (since 13^2 = 169 > 1000). Therefore, there are 5 additional kinda-prime numbers ([tex]2^2, 3^2, 5^2, 7^2, and 11^2[/tex]).
5. Add the total number of kinda-prime numbers from both cases: 168 + 5 = 173.
Learn more about integer here:
https://brainly.com/question/17118150
#SPJ11
[tex]$(\pi(1000)-1)+11=\boxed{177}$[/tex] "kind a-prime" positive integers less than $1000$.
Let [tex]$n$[/tex] be a positive integer with[tex]$k$[/tex] positive integer divisors.
If [tex]$k$[/tex] is prime, then.
[tex]$n$[/tex] is a "kind a-prime" integer.
[tex]$k$[/tex] must be of the form.
[tex]$k=p$[/tex] or [tex]$k=p^2$[/tex] for some prime [tex]$p$[/tex].
If [tex]$k=p$[/tex], then [tex]$n$[/tex] must be of the form.
[tex]$p^{p-1}$[/tex] for some prime [tex]$p$[/tex]. Since [tex]$p < 1000$[/tex], there are.
[tex]$\pi(1000)$[/tex]possible values of [tex]$p$[/tex].
[tex]$p=2$[/tex] gives [tex]$2^1$[/tex], which is not prime, so we have to subtract.
[tex]$1$[/tex] from [tex]$\pi(1000)$[/tex] to get the number of possible.
[tex]$p$[/tex].
[tex]$\pi(1000)-1$[/tex] values of [tex]$p$[/tex] that give a "kind a-prime" integer of this form.
If [tex]$k=p^2$[/tex], then [tex]$n$[/tex] must be of the form.
[tex]$p^{p^2-1}$[/tex] for some prime[tex]$p$[/tex].
There are.
[tex]$\pi(31)=11$[/tex] primes less than [tex]$31$[/tex], and each of them gives a different "kind a-prime" integer of this form.
Since [tex]$31^5 > 1000$[/tex], no primes larger than [tex]$31$[/tex]can be used to form a "kind a-prime" integer of this form.
[tex]$11$[/tex] possible values of [tex]$p$[/tex] that give a "kind a-prime" integer of this form.
For similar questions on Positive Integer
https://brainly.com/question/16952898
#SPJ11
a grocery store company wanted to know how well some of their local stores were doing. in order to find out, they hired three different reviewers to rate 10 local stores. the test statistic was 2.3, what is the p value?
Answers
Assuming a two-tailed test with 9 degrees of freedom (10 stores minus 1), the p-value for a t-value of 2.3 is approximately 0.040.
In order to calculate the p-value, we need to know the specific test being used and the significance level of the test. Let's assume that the test is a two-tailed t-test with a significance level of 0.05.
Since the test statistic is 2.3, we need to find the probability of getting a t-value of 2.3 or greater (in absolute value) under the null hypothesis. We can use a t-distribution table or a statistical software to find the corresponding p-value.
Assuming a two-tailed test with 9 degrees of freedom (10 stores minus 1), the p-value for a t-value of 2.3 is approximately 0.040. Therefore, if the significance level of the test is 0.05, we would reject the null hypothesis and conclude that there is a significant difference between the ratings given by the three reviewers.
To know more about statistic here
https://brainly.com/question/15525560
#SPJ4
You are helping with some repairs at home. You drop a hammer and it hits the floor at a speed of 4 feet per second. If the acceleration due to gravity (g) is 32 feet/second 2, how far above the ground (h) was the hammer when you dropped it? Use the formula:
Answers
Step-by-step explanation:
vf = vo + at vo = 0 in this case ( you dropped it from 'at rest')
4 f/s = 32 t
t = 1/8 s
df = do + vot + 1/2 at^2 df = final position = 0 ft (on the ground)
0 = do + 0 + 1/2 (-32)(1/8)^2
solve for do = 1/4 foot
If you spin the spinner 36 times, what is the best prediction possible for the number of times
it will land on green or blue?
Answers
The best prediction possible for the number of times the spinner will land on green or blue is given as follows:
30 spins.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
Out of six regions, three are green and two are blue, hence the probability of one spin resulting in green or blue is given as follows:
p = (3 + 2)/6
p = 5/6.
Thus the expected number out of 36 trials of spins resulting in green or blue is given as follows:
E(X) = 5/6 x 36
E(X) = 30 spins.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
armer abe has a budget of $300 to build a rectangular pen to protect his rambunctious sheep. he decides that three sides of the pen will be constructed with chain-link fence, which costs only $1 per foot. farmer abe decides that the fourth side of the pen will be made with sturdier fence, which costs $5 per foot. find the dimensions of the largest area the pen can enclose.
Answers
Let x be the length of the pen and y be the width of the pen.
The total cost of the pen is given by:
Cost = 3x + 5y = 300
3x + 5y = 300
3x = 300 - 5y
x = (300 - 5y)/3
The area of the pen is given by:
Area = xy = (300 - 5y)/3 * y
What is the slope of the line?
-2
-1
1
2
Answers
Answer: positive 2
Step-by-step explanation:
Solve for x please
Choices are...
10
5
25
90
Answers
Answer:
x = 10
Step-by-step explanation:
Angle form is = 90°
therefore
5x + 25 + x + 5 = 90
6x + 30 = 90
6x = 90-30
6x = 60
6x/6 = 60/6
x = 10
Complex numbers [tex]z[/tex] and [tex]w[/tex] satisfy [tex]|z|=|w|=1, |z+w|=\sqrt{2}[/tex].
What is the minimum value of [tex]P = |w-\frac{4}{z}+2(1+\frac{w}{z})i|[/tex]?
Answers
Okay, here are the steps to find the minimum value of P:
1) Given: |z|=|w|=1 (z and w are complex numbers with unit modulus)
|z+w|=sqrt(2)
Find z and w such that these conditions are satisfied.
Possible solutions:
z = 1, w = i (or vice versa)
z = i, w = 1 (or vice versa)
2) Substitute into P = |w-\frac{4}{z}+2(1+\frac{w}{z})i|
For the cases:
z = 1, w = i: P = |-1-4+2(1+i)i| = |-5+2i| = sqrt(25+4) = 5
z = i, w = 1: P = |1-\frac{4}{i}+2(1+\frac{1}{i})i| = |-3+2i| = sqrt(9+4) = 5
3) The minimum value of P is 5.
So in summary, the minimum value of
P = |w-\frac{4}{z}+2(1+\frac{w}{z})i|
is 5.
Let me know if you have any other questions!
g a generic drug is being tested to test its efficacy (effectiveness) at reducing blood pressure in patients with hypertension (a.k.a. high blood pressure). in a randomized, double-blind experiment with 200 patients, 100 are given the name-brand drug (control group) and 100 are given a generic version of the drug (treatment group). in the control group, the average reduction in blood pressure is 15.2 mmhg with a standard deviation of 11.5 mmhg. in the treatment group, there is an average reduction of 14.6 mmhg and a standard deviation of 12.5 mmhg. neither group has any outliers. a researcher claims that this study shows the generic drug is not as effective as the name-brand drug. what would be the reply of a statistician? you have two attempts for this problem so choose wisely. if you do not receive 5 points in the gradebook after submitting this assignment then you have answered incorrectly. make sure to try it again before the deadline.
Answers
A statistician would reply that in order to determine if the generic drug is less effective than the name-brand drug, a hypothesis test needs to be conducted.
The null hypothesis (H0) would be that there is no difference in the average blood pressure reduction between the two drugs, while the alternative hypothesis (H1) would be that the name-brand drug has a higher average reduction in blood pressure than the generic drug.
To test these hypotheses, a t-test would be appropriate since we have two independent samples (control and treatment groups) with known means, standard deviations, and sample sizes. The t-test will provide a p-value, which can be compared to a chosen significance level (e.g., α = 0.05).
If the p-value is less than the significance level, we reject the null hypothesis and conclude that there is a significant difference in the average blood pressure reduction between the two drugs. If the p-value is greater than the significance level, we fail to reject the null hypothesis, meaning we do not have enough evidence to claim that the name-brand drug is more effective than the generic drug.
Learn more about hypothesis:
https://brainly.com/question/10854125
#SPJ11
6) Practice: Using Visual Cues Label each part of the diagram. Then use your labels to complete the sentences. Square Root Notation √6 1. The expression √ means "the of b". 2. The exponent 1 symbol (√) stands for the 3. The number or expression under the radical symbol is called the
Answers
1. The expression √b means "the square root of b".
2. The radical symbol (√) stands for the exponent 1/2.
3. The number or expression under the radical symbol is called the radicand.
What is radicand?A radicand is the number or expression underneath a radical symbol (√). It is the number or expression that is being operated on by the root. The square root of the radicand is the result of the operation.
The expression √6 represents the square root of 6. This is the value of x that, when multiplied with itself, results in 6.
The square root of 6 is equal to 2.44948974, which is the positive solution to the equation x² = 6.
The radical symbol (√) indicates that the expression is a root and the number or expression under the radical symbol is called the radicand, which is 6 in this case.
The exponent of the radical symbol is 1/2, which implies that the expression is a square root.
For more questions related to expression
https://brainly.com/question/395066
#SPJ1
Show that cosh2x−sinh2x=1 � � � ℎ 2 � − � � � ℎ 2 � = 1 Differentiate with respect to x � e3xx2+1 � 3 � � 2 + 1 y=secx � = sec � y=tanx2 � = tan � 2 Differentiate with respect to x � y=ln(x+sinx) � = ln ( � + sin � ) y=cosxx2 � = cos � � 2 Find dydx � � � � given siny+x2y3−cosx=2y sin � + � 2 � 3 − cos � = 2 � Differentiate from first principles y=cosx � = cos � x3+2x2+3x+4 � 3 + 2 � 2 + 3 � + 4 Find d2ydx2 � 2 � � � 2 Given 3x3−6x2+2x−1 3 � 3 − 6 � 2 + 2 � − 1
Answers
We can conclude that cosh2x−sinh2x=1.
What is equation?An equation is a mathematical statement that states that two expressions are equal. It is typically written as a comparison between two expressions and consists of an equal sign (=). Equations are used to solve mathematical problems, to understand the relationships between different quantities, and to describe the behavior of a physical system. In addition, equations are used to calculate various quantities, such as the area of a circle or the speed of an object.
To show that cosh2x−sinh2x=1, we can use the identities for cosh2x and sinh2x. The identity for cosh2x is cosh2x=2cosh2x−1 and the identity for sinh2x is sinh2x=2sinh2x−1.
Substituting these identities into the equation cosh2x−sinh2x=1 yields 2cosh2x−1−2sinh2x−1=1. Simplifying this equation yields cosh2x−sinh2x=1, as required. Thus, we can conclude that cosh2x−sinh2x=1.
To know more about equation click-
http://brainly.com/question/2972832
#SPJ1
Simplifying this equation yields [tex]\cosh^2x-sinh^2x=1[/tex], as required. Thus, we can conclude that [tex]\cosh^2x-sinh^2x=1[/tex].
What is equation?An equation is a mathematical statement that states that two expressions are equal. It is typically written as a comparison between two expressions and consists of an equal sign (=). Equations are used to solve mathematical problems, to understand the relationships between different quantities, and to describe the behavior of a physical system. In addition, equations are used to calculate various quantities, such as the area of a circle or the speed of an object.
We will show that [tex]\cosh^2x-sinh^2x=1[/tex].
Let us consider the expression [tex]\cosh^2x-sinh^2x.[/tex]
Then, [tex]\cosh^2x=(e^2x+e^{-2}x)/2[/tex] and [tex]sinh^2x=(e^2x+e^{-2}x)/2[/tex]
Substituting, we get [tex]\cosh^2x -\sinh^2x=(e^2x+e^{-2}x)/2\ -(e^2x+e^{-2}x)/2[/tex]
Simplifying, we have [tex]\cosh^2x -\sinh^2x=e^2x+e^{-2}x-e^2x+e^{-2}x[/tex]
[tex]=2e^{-2}x\\\\=2(e^{-2}x)\\\\=2[/tex]
Hence, [tex]cosh^2x-sinh^2x=1[/tex]
Therefore, we have shown that [tex]cosh^2x-sinh^2x=1[/tex]
To know more about equation click-
brainly.com/question/2972832
#SPJ1
The correct form of question is Show that cosh2x−sinh2x=1 .
Lin plans to swim 12 laps in the pool. She has swum 9.75 laps so far.
How many laps does she have left to swim? Use y
for the number of laps that Lin has left to swim.
Answers
Lin plans to swim 12 laps and has already swum 9.75 laps, so the number of laps she has left to swim can be found by subtracting 9.75 from 12:
y = 12 - 9.75
Simplifying the right side:
y = 2.25
Therefore, Lin has 2.25 laps left to swim.
Which statement is true?
Please help
Answers
Ans-6
1. Find the height of the parabolic balloon arch for the prom when the position of the bottom anchors are at x = 3 feet and x = 7 feet.
Answers
The height of the parabolic balloon arch for the prom is 12.25 feet.
Using these assumptions, we can find the equation of the parabola that the arch follows as x = a(y-k)² + h, where (h,k) is the vertex and a is a constant that determines the shape of the parabola. We can find the value of a by using one of the points that the arch passes through, say (3,0):
3 = a(0-k)² + h h = 3 - a(k²)
Similarly, using the other point that the arch passes through, say (7,0):
7 = a(0-k)² + h h = 7 - a(k²)
Equating the expressions for h, we get:
3 - a(k²) = 7 - a(k²) a = -1/4
Substituting this value of a into one of the equations for h, say h = 7 - a(k²), we get:
h = 7 + 1/4(k²)
So the vertex of the parabola is at (h,k) = (7,0), and the equation of the parabola is x = -1/4(y² - 28y + 49).
To find the height of the arch, we need to find the y-coordinate of the vertex, which is k = 0. So the height of the arch is given by the distance between the vertex and the lowest point of the arch, which is the x-intercept of the parabola. To find the x-intercept, we set y = 0 in the equation of the parabola:
x = -1/4(0² - 28(0) + 49)
x = -1/4(49) = -12.25
However, since we are dealing with a physical object, the height cannot be negative. Therefore, we take the absolute value of the x-intercept, which gives us:
| -12.25 | = 12.25 feet
To know more about height here
https://brainly.com/question/10726356
#SPJ4
Find the volume of a pyramid with a square base, where the area of the base is 19. 6 ft 2 19. 6 ft 2 and the height of the pyramid is 11. 6 ft 11. 6 ft. Round your answer to the nearest tenth of a cubic foot
Answers
If the area of the base is 19. 6 ft^2 and the height of the pyramid is 11. 6 ft, the volume of the pyramid is approximately 79.1 cubic feet.
The formula for the volume of a pyramid is given by:
V = (1/3) × base area × height
In this case, we are given that the pyramid has a square base, so the base area is simply the area of a square with side length s:
base area = s^2 = 19.6 ft^2
We are also given the height of the pyramid:
height = 11.6 ft
Substituting these values into the formula for the volume of a pyramid, we get:
V = (1/3) × base area × height
= (1/3) × 19.6 ft^2 × 11.6 ft
≈ 79.1 ft^3 (rounded to the nearest tenth)
To learn more about volume click on,
https://brainly.com/question/23861754
#SPJ4
Hello solve this, what is 9 x 5/7
Answers
Answer: 6 3/7
Step-by-step explanation:
9/1 x 5/7
If we multiply the numerators and denominators, we get 45/7 or 6 3/7 as a mixed number.
Answer:
[tex]\frac{45}{7}[/tex] or 6.4285
Step-by-step explanation:
First, multiply 9 and 5, which gives you 45.
9(5)=45
Then, divide 45 by 7.
45/7=6.4285
That gives you [tex]\frac{45}{7}[/tex] or 6.4285
Hope this helps!
Joey deposits $6000 each into the two savings accounts described below. If he doesn’t make any other deposits or withdrawals, find the combined amount of accounts after 10 years.
Account 1
3.5% annual simple interest
Account 2
3.5% annual compound interest
Answers
The combined amount in both accounts after 10 years is $16,869.58
What is formula of simple interest and compound interest ?To solve the problem, we need to use the following formulas:
Simple Interest = Principal x Rate x Time
Compound Interest = [tex]Principal * (1 + Rate/ n)^{n * Time}[/tex]
where:
Principal = the initial deposit
Rate = the interest rate (in decimal form)
Time = the number of years
n = the number of times interest is compounded per year
For Account 1:
Simple Interest = Principal x Rate x Time
= $6000 x 0.035 x 10
= $2100
The amount in Account 1 after 10 years will be the initial deposit plus the interest earned:
= $6000 + $2100
= $8100
For Account 2:
Since the interest is compounded annually, n = 1.
Compound Interest = [tex]Principal * (1 + Rate/ n)^{n * Time}[/tex]
= [tex]6000 *(1 + 0.035/1)^{1 * 10}\\= $6000 (1.035)^{10}\\= $8769.58[/tex]
After ten years, the amount in Account 2 will be $8769.58.
After ten years, the combined amount in both accounts will be:
$8100 minus $8769.58 equals $16869.58, resulting in a total of $16,869.58 in both accounts after ten years.
know more about simple interest visit:
https://brainly.com/question/25845758
#SPJ1
the integers from 1 to 15, inclusive, are partitioned at random into two sets, one with 7elements and the other with 8. what is the probability that 1 and 2 are in the same set?
Answers
The chance/
probability
is
16/33
, or roughly 0.485 that 1 and 2 are in the
same set.
Let's say we divide the range of numbers from
1 to 15
into two sets, each containing seven and eight numbers, respectively. Finding the likelihood that the numbers 1 and 2 are included in the same
set
is our goal.
We can determine the
total number
of ways to divide the numbers into the two sets of
7
and
8
in order to begin solving this issue. Calculating this yields the result 6435 using a formula.
The number of ways in which the pairs 1 and 2 can be found in the same set must then be determined. Considering that there are
seven numbers
in the set, we must select six more from the remaining thirteen to complete the set, presuming that one is among the seven .There are
1716
ways to do this. The number of methods remains the same, 1716, even if we suppose that 2 is among the set of 7 numbers.
Hence, there are
3432
different ways to combine the numbers 1 and 2 into one set. The chance is 16/33, or roughly 0.485, when we divide this number by the total number of possible
divisions
of the numbers.
Learn more about
probability:
https://brainly.com/question/14210034
#SPJ4