Use the equation below to answer the question. 6x + 3 = 3(2x + 3) Which statement correctly explains whether the equation is true or not?
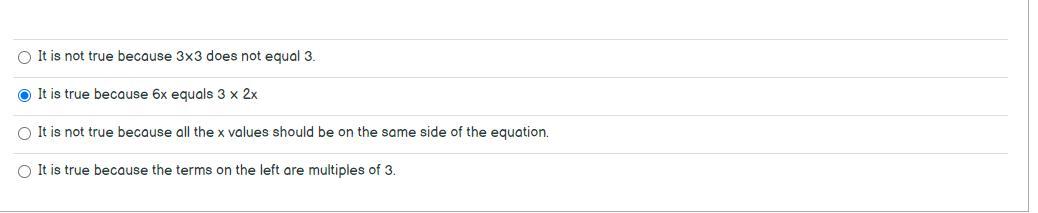
Answers
Answer:
It should be the first one
Step-by-step explanation:
3x2=6
3x3=9
Related Questions
five balls are numbered through and placed in a bowl. josh will randomly choose a ball from the bowl, look at its number and then put it back into the bowl. then josh will again randomly choose a ball from the bowl and look at its number. what is the probability that the product of the two numbers will be even and greater than express your answer as a common fraction.
Answers
The probability that the product of the two chosen numbers will be even and greater than 2 is 9/25.
What is probability?Probability is a measure of the likelihood or chance of a particular event occurring. It is expressed as a number between 0 and 1, where 0 represents an impossible event that will not occur, and 1 represents a certain event that will always occur.
According to the given information:
There are 5 balls numbered 1 through 5 in the bowl. The total number of possible outcomes, when Josh chooses a ball, is 5, as there are 5 balls in the bowl.
Now let's consider the probability of choosing a ball with an even number. There are 3 even numbers (2, 4, and 5) out of the 5 possible numbers, so the probability of choosing a ball with an even number is 3/5.
Next, let's consider the probability of choosing a ball with a number greater than 2. There are 3 numbers (3, 4, and 5) greater than 2 out of the 5 possible numbers, so the probability of choosing a ball with a number greater than 2 is also 3/5.
To find the probability that the product of the two chosen numbers will be even and greater than 2, we need to multiply the probabilities of choosing an even number and choosing a number greater than 2.
Probability of choosing an even number: 3/5
Probability of choosing a number greater than 2: 3/5
Multiplying these probabilities, we get:
(3/5) * (3/5) = 9/25
So, the probability that the product of the two chosen numbers will be even and greater than 2 is 9/25.
To know more about Probability visit:https://brainly.com/question/11234923
#SPJ1
write an integral that quantifies the change in the area of the surface of a cube when its side length quadruples from s unit to 4s units.
Answers
Answer:
Step-by-step explanation:
Let A be the area of the surface of the cube.
When the side length changes from s to 4s, the new area A' can be calculated as:
A' = 6(4s)^2 = 96s^2
The change in area is then:
ΔA = A' - A = 96s^2 - 6s^2 = 90s^2
To find the integral that quantifies the change in area, we can integrate the expression for ΔA with respect to s, from s to 4s:
∫(90s^2)ds from s to 4s
= [30s^3] from s to 4s
= 30(4s)^3 - 30s^3
= 1920s^3 - 30s^3
= 1890s^3
Therefore, the integral that quantifies the change in area of the surface of a cube when its side length quadruples from s units to 4s units is:
∫(90s^2)ds from s to 4s
= 1890s^3 from s to 4s
= 1890(4s)^3 - 1890s^3
= 477,840s^3 - 1890s^3
In a 10-kilometer race, there are no race
monitors for the first kilometer. After
that, there are race monitors every
0.25 kilometer, including at the finish
line. How many race monitors are there
Answers
Therefore, there are 37 race monitors in the entire 10-kilometer race.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It usually contains one or more variables, and the goal is to find the value of the variable(s) that satisfies the equation. An equation can be written in various forms, such as standard form, slope-intercept form, or general form, depending on the type of equation and the information given. Equations are used in many areas of mathematics, science, and engineering to model and solve problems.
Here,
There are race monitors every 0.25 kilometers, so we can divide the race into segments of 0.25 kilometers.
The first segment is from 1 kilometer to 1.25 kilometers. Since there are no monitors for the first kilometer, we only need to count the monitors from 1 kilometer to the finish line.
To find the number of monitors from 1 kilometer to the finish line, we can subtract 1 from the total distance of the race and then divide by 0.25 (since there is a monitor every 0.25 kilometers after the first kilometer):
(10 - 1) / 0.25 = 36
So there are 36 race monitors from 1 kilometer to the finish line. But since there are no monitors for the first kilometer, we need to add 1:
36 + 1 = 37
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
Find the missing side or angle. Round to the nearest tenth. A=45° B=100° c=15 a=[?]
Answers
The offered triangle's missing side measures 18.5 inches.
Two angles and one side of a triangle are measured as follows: A = 45°, B = 100°, and c = 15.
We need to find the side a. [opposite to angle A]
The Law of Sines indicates that we can use this formula to get the missing side (a) in the triangle given:
[tex]\mathrm{\frac{a}{sin(A)} = \frac{c}{sin(C)}}[/tex]
where A is the angle opposite side A, C is the angle opposite side C, and an is the unknown side.
Let's plug in the values we have:
A = 45°
B = 100°
c = 15
Now, we can find angle C using the fact that the sum of angles in a triangle is 180°:
C = 180° - A - B
C = 180° - 45° - 100°
C = 35°
Now we can apply the Law of Sines to find side a:
[tex]\mathrm {\frac{a}{sin(45)} = \frac{15}{sin(35)}}[/tex]
To find a, let's first calculate the values of sin(45°) and sin(35°):
sin(45°) ≈ 0.7071
sin(35°) ≈ 0.5736
Now, solve for a:
[tex]\frac{a}{0.7071} = \frac{15}{0.5736}[/tex]
a ≈ (15 × 0.7071) / 0.5736
a ≈ 18.54
Rounding to the nearest tenth:
a ≈ 18.5
So, the missing side (a) is approximately 18.5 units.
Learn more about Law of Sines click;
https://brainly.com/question/21634338
#SPJ12
Solve for X, please write an explanation.
Answers
Step-by-step explanation:
2x+20 and 2x-4 are supplementary angles...they form a straight line and thus = 180 degrees when added together
2x+20 + 2x-4 = 180 simplify
4x + 16 = 180 subtract 16 from both sides
4x = 164 divide both sides by 4
x = 41 degrees
Transformations Task Card # 29 What is the image of point (3,4) after a dilation of 2? New Coordinate
Answers
Answer:
(6, 8)
Step-by-step explanation:
A dilation scales an object on the coordinate plane using the scale factor, causing it to get bigger or smaller.
We are given that the point (3, 4) is dilated by 2; since 2 is greater than 1, this is an enlargement (in which the figure gets bigger).
So, all we need to do is multiply each of the coordinates by 2, like so:
[tex]3*2=6\\4*2=8[/tex]
Thus, the image of the point (3, 4), after being dilated by 2, is (6, 8).
in a recent poll of 1200 randomly selected adult office workers, 32% said they had worn a halloween costume to the office at least once. what is the margin of error, using a 95% confidence level, for estimating the true population proportion of adult office workers who have worn a halloween costume to the office at least once?
Answers
The margin of error for estimating the true population proportion of adult office workers who have worn a Halloween costume to the office at least once, using a 95% confidence level, is approximately 0.02633 .
What is known by random variable?A random variable is a variable whose value is unknown, or a function that assigns values to each of an experiment's outcomes.
What is meant by proportion?A proportion is an equation in which two ratios are set equal to each other.
The margin of error for estimating the true population proportion can be calculated using the formula:
Margin of Error = Critical Value * Standard Deviation
where the Critical Value is determined based on the desired confidence level and the Standard Deviation is an estimate of the variability of the population proportion.
Given that the sample size is large (n = 1200) and we are using a 95% confidence level, we can use the standard normal distribution (Z-distribution) for the Critical Value. The critical value for a 95% confidence level in a standard normal distribution is approximately 1.96.
The Standard Deviation can be estimated using the sample proportion, which is given as 32% or 0.32 in this case. The sample proportion is a point estimate of the population proportion.
Using these values, we can calculate the margin of error as follows:
Margin of Error = 1.96 * √( (0.32 * (1 - 0.32)) / 1200 )
= 1.96 * √( 0.2176 / 1200 )
= 1.96 * √( 0.00018133333 )
= 1.96 * 0.01345451543
= 0.02633 (rounded to 5 decimal places)
So, the margin of error for estimating the true population proportion of adult office workers who have worn a Halloween costume to the office at least once, using a 95% confidence level, is approximately 0.02633 .
Learn more about decimal here:
https://brainly.com/question/30958821
#SPJ1
A student was asked to form different triangles with angle measures of 90 degrees, 30 degrees, and 60 degrees. She incorrectly said this triangle is the only triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees. What mistake might she have made
Answers
The student's mistake might have been that she assumed that there is only one possible triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees. However, this is not true.
what is triangle ?
A triangle is a three-sided polygon, which is a closed two-dimensional shape with straight sides. It is one of the basic shapes in geometry and is used in various fields such as mathematics, physics, engineering, and architecture.
In the given question,
The student's mistake might have been that she assumed that there is only one possible triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees. However, this is not true. In fact, there are infinitely many triangles with these angle measures, since the length of the sides can vary.
The most well-known triangle with angle measures of 90 degrees, 30 degrees, and 60 degrees is the 30-60-90 triangle, which has specific side ratios of 1:sqrt(3):2. But this is just one possible example of a triangle with those angle measures, and it is not the only one.
It is important to note that in a triangle, the angles determine the shape and the side lengths determine the size. Therefore, if two triangles have the same angle measures, they will be similar, but they may not necessarily be congruent unless they also have the same side lengths.
To know more about triangle , visit:
https://brainly.com/question/2773823
#SPJ1
Determine the domain of the following graph:
21098
11
76
4
+32
2
1
-12-11-10-9-8-7-6-5-4-3-2-1
5
ܐ ܣ ܣ ܟ ܬ ܬ { ܣ ܣ
-2
-3
-4
-5
-6
-9
-7
-10
-8
-11
-12
2 3 4 5 6 7 8 9 10 11 12
Answers
The domain of the following graph is equal to [-11. -3]
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function is defined.
How to identify the domain any graph?In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-11, -3].
Range = [-5, 0].
Read more on domain here: brainly.com/question/9765637
#SPJ1
This past semester, a professor had a small business calculus section. The students in the class were William comma Mike comma Allison comma Kristin comma Jim comma Neta comma Pam comma and Jinita. Suppose the professor randomly selects two people to go to the board to work problems. What is the probability that Neta is the first person chosen to go to the board and Jinita is the second?
Answers
The probability that Neta is chosen first and Jinita is chosen second is:
1/56(or approximately 0.018.)
There are 8 students in class, so there are 8 choices for first person and 7 choices for second person.
Since we want to calculate probability that Neta is chosen first and Jinita is chosen second, we need to consider the number of ways in which these two students can be chosen in that order.
There is only one way for Neta to be chosen first and Jinita to be chosen second, so the total number of possible outcomes is:
8 x 7 = 56
Therefore, the probability that Neta is chosen first and Jinita is chosen second is: 1/56 or approximately 0.018.
To know more about probability, here
brainly.com/question/30034780
#SPJ4
Select the correct answer. Sides of three square rooms measure 14 feet each, and sides of two square rooms measure 17 feet each. Which expression shows the total area of these five rooms? A. (3 × 14^2) + (2 × 17^2) B. (2 × 14^3) + (2 × 17^2) C. (3 × 17^2) + (2 × 14^2) D. (3 × 14^2) × (2 × 17^2) Reset Next
Answers
The correct expression showing the total area of the five rooms is A. (3 x 14²) + (2 x 17²), which simplifies to 1918 square feet.
What is expression?An expression is a combination of numbers, symbols, and operators (such as addition, subtraction, multiplication, and division) that represent a mathematical calculation. An expression can be a single number, a variable, or a combination of both, and can be used to represent mathematical formulas, equations, or relationships.
In the given question,
C. (3 × 17²) + (2 × 14²)
To find the total area of the five rooms, we need to add the area of each room. The area of a square is found by squaring the length of one side.
For the three rooms with sides of 14 feet each, the area of each room is:
14^2 = 196 square feet
So the total area of these three rooms is:
3 × 196 = 588 square feet
For the two rooms with sides of 17 feet each, the area of each room is:
17^2 = 289 square feet
So the total area of these two rooms is:
2 × 289 = 578 square feet
Therefore, the total area of all five rooms is:
588 + 578 = 1166 square feet
Option C, (3 × 17²) + (2 × 14²), gives the correct expression for this calculation.
To know more about expression, visit:
https://brainly.com/question/2559684
#SPJ1
I don’t know what to write for the equation.
Answers
fraction wise, a whole is always simplified to 1, so
[tex]\cfrac{4}{4}\implies \cfrac{1000}{1000}\implies \cfrac{9999}{9999}\implies \cfrac{17}{17}\implies \text{\LARGE 1} ~~ whole[/tex]
so, we can say the whole of the players, namely all of them, expressed in fourth is well, 4/4, that's the whole lot, and we also know that 3/4 of that is 12, the guys who chose the bottle of water
[tex]\begin{array}{ccll} fraction&value\\ \cline{1-2} \frac{4}{4}&p\\[1em] \frac{3}{4}&12 \end{array}\implies \cfrac{~~ \frac{4 }{4 } ~~}{\frac{3}{4}}~~ = ~~\cfrac{p}{12}\implies \cfrac{~~ 1 ~~}{\frac{3}{4}} = \cfrac{p}{12}\implies \cfrac{4}{3}=\cfrac{p}{12} \\\\\\ (4)(12)=3p\implies \cfrac{(4)(12)}{3}=p\implies 16=p[/tex]
Please fill in all of the blanks
Answers
Answer:
The perimeter of this trapezoid is
7 + 5 + 3 + 7 + 4 = 26 cm
rectangle, A = lw, 4 × 7 = 28 square cm
triangle, A = (1/2)bh, (1/2) × 3 × 4 =
6 square cm
(1/2)(4)(7 + 10) = (1/2)(4)(17) = 34 square cm = 28 square cm + 6 square cm
A sector of a circle has a central angle of 120°.
Find the area of the sector if the radius of the circle is 8cm. (Round your answer to two decimal place.)
Answers
Rounding to two decimal places, the area of the sector is approximately 67.02cm².
What is area?Area is a measurement of the size of a two-dimensional surface, such as the surface of a flat object or the ground. It is expressed in units of square units, such as square meters or square feet.
Here,
To find the area of the sector of a circle, we need to know the measure of the central angle and the radius of the circle. In this case, we are given that the central angle is 120° and the radius of the circle is 8cm. We can use the formula for the area of a sector of a circle:
Area of sector = (central angle/360°) x πr²
where r is the radius of the circle and π is a constant approximately equal to 3.14.
Plugging in the values we have:
Area of sector = (120°/360°) x π(8cm)²
Area of sector = (1/3) x π(64cm²)
Area of sector = (1/3) x 201.06cm²
Area of sector = 67.02cm²
To know more about area of sector,
https://brainly.com/question/7512468
#SPJ1
April is considering a 7/23 balloon mortgage with an interest rate of 4.15% to
purchase a house for $197,000. What will be her balloon payment at the end
of 7 years?
OA. $173,819.97
OB. $170,118.49
OC. $225,368.29
OD. $170,245.98
SUBMIT
Answers
The balloon payment at the end of 7 years would be $173,819.97, which is option A.
How to find the balloon payment at the end of 7 yearsA 7/23 balloon mortgage means that April will make payments on the loan as if it were a 23-year mortgage, but the remaining balance of the loan will be due in full after 7 years.
To find the balloon payment at the end of 7 years, we can first calculate the monthly payment using the loan amount, interest rate, and loan term:
n = 23 * 12 = 276 (total number of payments)
r = 4.15% / 12 = 0.003458 (monthly interest rate)
P = (r * PV) / (1 - (1 + r)^(-n))
where
PV is the present value of the loan (the loan amount)n is the total number of paymentsr is the monthly interest ratePV = $197,000
P = (0.003458 * $197,000) / (1 - (1 + 0.003458)^(-276)) = $1,007.14 (monthly payment)
Now we can calculate the remaining balance on the loan after 7 years. Since April is making payments as if it were a 23-year mortgage, she will have made 7 * 12 = 84 payments by the end of the 7th year.
Using the formula for the remaining balance of a loan after t payments:
B = PV * (1 + r)^t - (P / r) * ((1 + r)^t - 1)
Where
B is the remaining balancePV is the initial loan amount r is the monthly interest rateP is the monthly payment t is the number of payments madet = 84 (number of payments made)
B = $197,000 * (1 + 0.003458)^84 - ($1,007.14 / 0.003458) * ((1 + 0.003458)^84 - 1)
B = $173,819.97
Therefore, the balloon payment at the end of 7 years would be $173,819.97, which is option A.
Learn more about monthly payment here : brainly.com/question/28106777
#SPJ1
we will eventually see using the theory of taylor series that can be computed using an infinite series: which convergence test shows that the series does in fact converge?
Answers
A number of
convergence tests
can be used to examine a Taylor series' convergence, but the Ratio Test is one that is frequently employed. According to the
ratio test, the series converges absolutely if the limit of the
absolute value
of the ratio of the (n+1)th term to the nth term is smaller than 1. In mathematics, this is expressed as:
lim┬(n→∞)〖|a_(n+1)/a_n |<1〗
where a n is the
series' nth term. The series
diverges
if the limit is bigger than 1, and extra tests must be employed if the limit is equal to 1.
Although the
Ratio Test
is a frequently used test for
Taylor series
convergence, it is not always appropriate and other tests can be required based on the unique characteristics of the series.
Learn more about
Taylor series
:
https://brainly.com/question/28158012
#SPJ4
Determine two coterminal angles (one positive and one negative) for each angle. Give your answers in radians. (Enter your answers as a comma-separated list.)
(a)
3/4
Answers
The two coterminal angles for 3/4 radians are (3π + 4)/4 and (-5π + 4)/4 radians.
What is coterminal angles ?Coterminal angles are two or more angles that have the same initial and terminal sides, but differ by a multiple of 360 degrees or 2π radians. In other words, coterminal angles are angles that overlap each other when drawn in standard position (with their initial side on the positive x-axis).
To find two coterminal angles with 3/4 radians, we can add or subtract multiples of 2π radians (which is equivalent to a full circle).
One positive coterminal angle is obtained by adding 2π radians to 3/4 radians:
3/4 + 2π = 3/4 + 8π/4 = 3/4 + 2π
Simplifying, we get:
3/4 + 2π = (3π + 4)/4
Therefore, one positive coterminal angle is (3π + 4)/4 radians.
One negative coterminal angle is obtained by subtracting 2π radians from 3/4 radians:
3/4 - 2π = 3/4 - 8π/4 = 3/4 - 2π
Simplifying, we get:
3/4 - 2π = (-5π + 4)/4
Therefore, one negative coterminal angle is (-5π + 4)/4 radians.
Hence, the two coterminal angles for 3/4 radians are (3π + 4)/4 and (-5π + 4)/4 radians.
To know more about coterminal angles visit:
https://brainly.com/question/23093580
#SPJ1
Alfred buys a car for £13960 which depreciates in value at a rate of 0.75% per year.
Work out how much Alfred's car will be worth in 12 years.
Answers
Answer:
£12063.57
Step-by-step explanation:
The value of Alfred’s car after 12 years can be calculated using the formula for exponential decay: Final Value = Initial Value * (1 - rate of depreciation)^(number of years). Plugging in the values we get: Final Value = 13960 * (1 - 0.0075)^12. Therefore, after 12 years, Alfred’s car will be worth approximately £12063.57.
If you watch from ground level, a child riding on a merry-go-round will seem to be undergoing simple harmonic motion from side to side. Assume the merry-go-round is 10.6 feet across and the child completes 8 rotations in 120 seconds. Write a sine function that describes d, the child's apparent distance from the center of the merry-go-round, as a function of time t.
Answers
The sine function that describes the child's apparent distance from the center of the merry-go-round is d(t) = 5.3 sin(2π/15 * t)
How to write a sine function that describes the child's apparent distance?To write a sine function that describes the child's apparent distance from the center of the merry-go-round as a function of time t, we can start by finding the amplitude, period, and phase shift of the motion.
Amplitude:
The amplitude of the motion is half the diameter of the merry-go-round, which is 10.6/2 = 5.3 feet. This is because the child moves back and forth across the diameter of the merry-go-round.
Period:
The period of the motion is the time it takes for the child to complete one full cycle of back-and-forth motion, which is equal to the time it takes for the merry-go-round to complete one full rotation.
From the given information, the child completes 8 rotations in 120 seconds, so the period is T = 120/8 = 15 seconds.
Phase shift:
The phase shift of the motion is the amount of time by which the sine function is shifted horizontally (to the right or left).
In this case, the child starts at one end of the diameter and moves to the other end, so the sine function starts at its maximum value when t = 0. Thus, the phase shift is 0.
With these values, we can write the sine function that describes the child's apparent distance from the center of the merry-go-round as:
d(t) = 5.3 sin(2π/15 * t)
where d is the child's distance from the center of the merry-go-round in feet, and t is the time in seconds. The factor 2π/15 is the angular frequency of the motion, which is equal to 2π/T.
Learn more about sine function on:
https://brainly.com/question/30243373
#SPJ1
the ratio of a time a student spends on their art project to time spent on their science project is 3:4.The total amount of time the student spends on projects for these 56 min.How much does the students spend on projects for each subject
Answers
Answer: the student spends 24 minutes on their art project and 32 minutes on their science project.
Step-by-step explanation:
Answer:
The student spends 24 minutes on their art project, and 32 minutes on their science project
Step-by-step explanation:
To solve this problem, we can utilise the unitary method, a process by which we find the value of a single unit, from the value of multiple units and thus, the value of multiple units from the value of a single unit.
If the total number of units in the ratio is (3+4)=7, then 7 units = 56 mins.
If 7 units = 56 mins,
then 1 unit = 56/7 mins = 8 mins.
Therefore, 3 units = 8×3 = 24 mins,
and 4 units = 8×4 = 32 mins.
Thus, the student spends 24 minutes on their art project, and 32 minutes on their science project
help please without guessing ?//
Answers
Answer:
D. y ≥ x² - 4x - 5
Step-by-step explanation:
We can observe two characteristics of this graphed inequality:
1. its shading is above it, therefore the inequality sign must be greater than
2. its boundary line is continuous, not dotted, so the inequality sign must include or equal to
From these two observations, we can assert that D. x² - 4x - 5 is the correct answer because it is the only one which has a greater than or equal to sign.
____________
Note:
We can also check that the equation for the inequality is correct by converting it to vertex form by completing the square, then graphing it ourselves:
[tex]y \ge (x-2)^2 - 9[/tex]
Answer:
The answer is y≥ x²-4x-5
Step-by-step explanation:
x=a,x=b
where a,b are roots of the equation
a= -1 b=5
x= -1,x=5
x+1=0,x-5=0
(x+1)(x-5)=0
x²-5x+x-5=0
x²-4x-5=0
Write the equation of the line that passes through the point (0, 4) and is parallel to the line with equation y=5x+3
Answers
Sorry if my english is a bit weird, i hope that helped!
three hundred students in a school were asked to select their favorite fruit from a choice of apples, oranges, and mangoes. this table lists the results. if a survey is selected at random, what is the probability that the student is a girl who chose apple as her favorite fruit? answer choices are rounded to the hundredths place.
Answers
The probability that a student selected at random is a girl who chose apple as her favorite fruit is 0.32, or 32% rounded to the nearest hundredth.
To calculate the probability that a student is a girl who chose apple as her favorite fruit, we need to use the information provided in the table. First, we need to find the total number of girls who participated in the survey, which is the sum of the number of girls who chose apples, oranges, and mangoes as their favorite fruit, i.e., 46 + 41 + 55 = 142.
Next, we need to find the number of girls who chose apples as their favorite fruit, which is 46. Therefore, the probability that a student is a girl who chose apple as her favorite fruit is given by:
Probability = Number of girls who chose apples / Total number of girls in the survey
Probability = 46 / 142
Probability = 0.32
This means that out of all the girls who participated in the survey, 32% of them chose apple as their favorite fruit.
To learn more about probability click on,
https://brainly.com/question/30622026
#SPJ4
Complete question is:
three hundred students in a school were asked to select their favorite fruit from a choice of apples, oranges, and mangoes. this table lists the results.
Boys Girls
Apple 66 46
Orange 52 41
Mango 40 55
if a survey is selected at random, what is the probability that the student is a girl who chose apple as her favorite fruit?
HELP MARKING BRAINLEIST
Answers
Answer:
r = 2
center: ( -7,0 )
Step-by-step explanation:
Find the domain for each expression. 1/x
Answers
The domain of function 1/x is (-∞, 0) U (0, ∞), which means all real numbers except 0.
What is a domain?In mathematics, the term "domain" refers to the set of possible input values for a function, equation, or expression. The domain represents the valid inputs that can be used to evaluate the function or expression and obtain a meaningful output.
For example, consider the function f(x) = x^2. The domain of this function is all real numbers because we can plug in any real number for x and obtain a valid output. However, if we consider the function g(x) = 1/x, the domain of this function is all real numbers except x = 0, because division by zero is undefined and we cannot evaluate the function at that point.
According to the given informationThe expression 1/x has a domain of all real numbers except x = 0. This is because division by zero is undefined, so the expression is not defined for x = 0. For all other values of x, we can evaluate 1/x and get a real number. Therefore, the domain of 1/x is (-∞, 0) U (0, ∞), which means all real numbers except 0.
To know more about the domain visit:
brainly.com/question/29452843
#SPJ1
what minus 1 1/2 equals 3 3/4
Answers
Answer:
5 1/4
Step-by-step explanation:
An analyst is interested in testing the hypothesis that stock betas are higher in a down market (when the market index returns are negative) than otherwise.
Write the regression equation you would employ to test the analyst’s hypothesis.
Answers
This supports the analyst's hypothesis that betas are higher in down markets.
What is the meaning of equations?In algebra, the definition of an equation, in its simplest form, is a mathematical statement that shows that two mathematical expressions are equal. For example, 3x + 5 = 14 is an equation where 3x + 5 and 14 are two expressions separated by the equation.
To test the hypothesis that stock betas are higher in bear markets, we use the following regression equation:
Ri = αi + βi(Rm) + εi
where,
Ri = return on ith stock
Rm = market return
αi = intercept (constant term) of the regression equation of the ith stock.
βi = slope of the market return of the ith stock (regression coefficient).
εi = error period of the ith stock
To test the hypothesis, we include an additional variable in the regression equation that describes the effect of the market return when it is negative. This variable would be a dummy variable that takes the value 1 if the market return is negative and 0 otherwise. Let's call this variable D. So the modified regression equation would be:
Ri = αi + βi(Rm) + γiD + εi
where,
γi = the excess regression coefficient of the ith stock that describes the effect of the market return when it is negative
The coefficient γi measures the difference between the beta value of a stock between a falling market and a non-falling market. If γi is significantly greater than 0, this supports the analyst's hypothesis that betas are higher in down markets.
Learn more about algebra here
https://brainly.com/question/24875240
#SPJ1
find the best estimate for the unicity distance for affine cipher. group of answer choices 1.33 2.35 3.33 2.66 1.75
Answers
The closest answer choice to this value is option 1, 33. Therefore, the best estimate for the unicity distance for an affine cipher is 33.
To find the best estimate for the unicity distance for an affine cipher, we can use the following formula:
Unicity Distance (U) = (keyspace / entropy) × log2(1 / redundancy).
Given the answer choices:
1. 33
2. 35
3. 33
4. 26
5. 17.5
For an affine cipher, the keyspace is 26^2 (since there are 26 possibilities for both 'a' and 'b' in the equation
y = (ax + b) mod 26).
The entropy of English text is roughly 1.5 bits/character, and the redundancy is approximately 0.7.
Using the formula, we have:
U = (26^2 / 1.5) × log2(1 / 0.7)
U ≈ 33.49
Therefore, the best estimate for the unicity distance for an affine cipher is 33.
for such more question on unicity distance
https://brainly.com/question/31483371
#SPJ11
a recent survey revealed that 30% of us households own one or more cats. you visit 50 random households. what is the mean number of households that will have one or more cats? 15 what is the standard deviation of the number of households that will have one or more cats? 3.2 round your answer to 1 decimal place. suppose that 10 of the 50 random households had one or more cats. would you consider this unusual?
Answers
1. The mean number of households that will have one or more cats is 15.
2. This means that getting 10 or fewer households with cats out of 50 is not extremely unusual, as there is a 5.3% chance of it happening by random chance alone.
The mean number of households that will have one or more cats can be calculated as:
Mean = (30/100) x 50 = 15
Therefore, the mean number of households that will have one or more cats is 15.
The standard deviation can be calculated using the formula:
Standard deviation = [tex]\sqrt{(npq)}[/tex]
where n is the sample size (50), p is the probability of success (30/100 = 0.3), and q is the probability of failure (1 - p = 0.7).
Standard deviation = sqrt(50 x 0.3 x 0.7) = 3.08
Rounding to 1 decimal place, the standard deviation is 3.1.
If 10 of the 50 random households had one or more cats, we can calculate the z-score as:
z = (x - μ) / σ
where x is the observed number of households with cats (10), μ is the mean (15), and σ is the standard deviation (3.1).
z = (10 - 15) / 3.1 = -1.61
Looking up the z-score in a standard normal distribution table, we find that the probability of getting a z-score of -1.61 or lower is 0.053.
This means that getting 10 or fewer households with cats out of 50 is not extremely unusual, as there is a 5.3% chance of it happening by random chance alone.
However, it is somewhat lower than the expected value of 15, which suggests that the sample may not be fully representative of the population.
For similar question on mean.
https://brainly.com/question/28225633
#SPJ11
Graph Y = 1/2x - 4 on the coordinate plane
Answers
The x-axis and y-axis are two parallel number lines that meet at (0, 0) to form the shape of the letter t.
Describe Coordinate Plane?Geometric objects and mathematical equations are represented on the coordinate plane, a two-dimensional graph. It is made up of the x-axis and y-axis, two parallel number lines that meet at the starting point (0, 0). The horizontal coordinate is represented by the x-axis, while the vertical coordinate is represented by the y-axis. They combine to create the Cartesian coordinate system.
Positive numbers are labelled to the right of the origin and negative values are labelled to the left of the origin on the x-axis. Positive numbers are written above the origin of the y-axis, and negative numbers are written below it. An ordered pair (x, y), where x denotes the horizontal coordinate and y denotes the vertical coordinate, is used to represent each point on the coordinate plane.
For graphing linear equations, quadratic equations, and other functions, the coordinate plane is a helpful tool. Additionally, it is employed to depict geometric forms like polygons, circles, and lines. The distance between two points, the slope of a line, and other significant features of mathematical objects can be calculated by graphing points on the coordinate plane. With applications in physics, engineering, economics, and computer science, the coordinate plane is a fundamental idea in mathematics.
The graph is shown below when y=1.
To know more about graph visit:
brainly.com/question/31090865
#SPJ1
Graph attached below,
The coordinates of the plane is
x y
1 -3.5
2 -3
4 -2
6 -1.
What is equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.
Here the given equation is y = [tex]\frac{1}{2}x-4[/tex].
Now put x= 1 then y = [tex]\frac{1}{2}\times1-4 =\frac{1-8}{2}=\frac{-7}{2}=-3.5[/tex]
Now put x=2 then [tex]y=\frac{1}{2}\times2-4=1-4=-3[/tex]
Now put x=4 then [tex]y=\frac{1}{2}\times4-4=2-4=-2[/tex]
Now put x=6 then [tex]y=\frac{1}{2}\times6-4=3-4=-1[/tex]
Then coordinates of the plane is
x y
1 -3.5
2 -3
4 -2
6 -1.
To learn more about equation refer the below link
https://brainly.com/question/29336774
#SPJ1