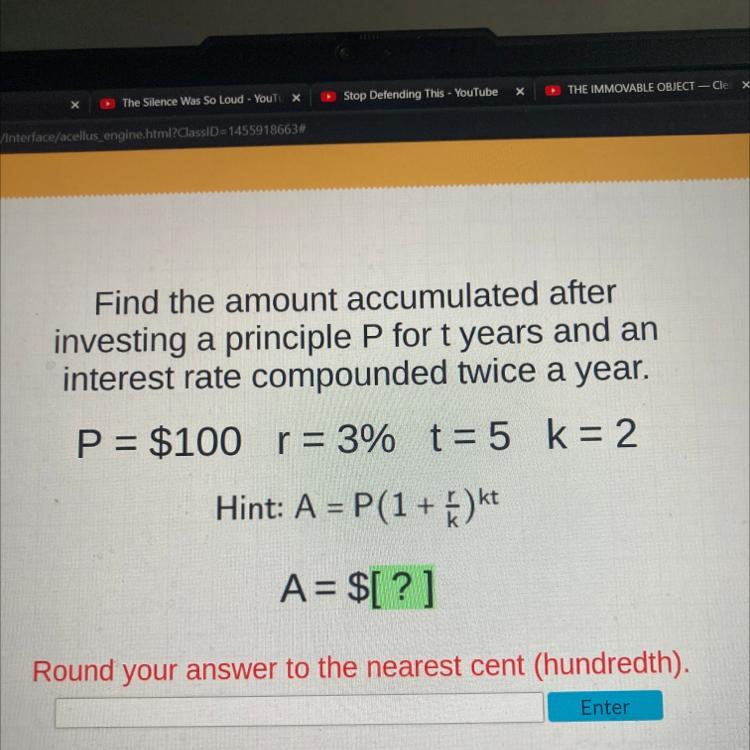
Find the amount accumulated after
investing a principle P for t years and an
interest rate compounded twice a year.
P = $100 r = 3% t= 5 k = 2
Hint: A = P(1 + E)kt
A = $[?]

The range of the 98% confidence interval for the percentage of faulty components that differ between machines A and B is about between -0.2448 and 0.1305. (rounded to 4 decimal places).

Given:

Sample proportion from machine A ([tex]p_1[/tex]) = 5/35 = 0.14285714285714285

Sample proportion from machine B ([tex]p_2[/tex]) = 7/35 = 0.2

Sample size from machine A ([tex]n_1[/tex]) = 35

Sample size from machine B ([tex]n_2[/tex]) = 35

Standard error (SE) = [tex]\sqrt{ [(p1 * (1 - p1) / n1) + (p2 * (1 - p2) / n2)}[/tex]

= [tex]\sqrt{[0.14285714285714285 * (1 - 0.14285714285714285) / 35] + [0.2 * (1 - 0.2) / 35] }[/tex]

= 0.07058061453775912 (rounded to 11 decimal places)

Margin of error (ME) = Critical value * Standard error

= 2.660 * 0.07058061453775912 (using z-score for a 98% confidence level)

= 0.18765117789861733 (rounded to 11 decimal places)

Confidence interval (CI) = Sample statistic ± Margin of error

= [tex](p_1 - p_2) \pm ME[/tex]

= (0.14285714285714285 - 0.2) ± 0.18765117789861733

= -0.05714285714285715 ± 0.18765117789861733

The 98% confidence interval for the difference in proportions of defective parts between machine A and machine B is approximately -0.2448 to 0.1305 (rounded to 4 decimal places).

Learn more about confidence interval here:

https://brainly.com/question/29680703

#SPJ1

Answer: Using the formula i = prt, we have:

i = (104292.12 - 80040) = 24252.12

p = 80040

t = 3

Substituting these values, we get:

24252.12 = 80040 * r * 3

Solving for r, we get:

r = 0.101 or 10.1%

Therefore, the interest rate is 10.1%.

Step-by-step explanation:

So, the area of triangle DEF is 312.5 square feet, using the scale factor of 5/2.

the context of mathematics and geometry, dilation is a transformation that changes the size of an object. It is a type of transformation that scales an object by a certain factor, without changing its shape or orientation.

In other words, dilation involves multiplying the coordinates of a geometric figure by a fixed constant, which results in an enlarged or reduced version of the original figure. The constant is known as the dilation factor or the scale factor, and it can be any real number greater than zero.

For example, if we dilate a circle by a scale factor of 2, every point on the circle will be moved twice as far away from the center, resulting in a new circle with a diameter twice as large as the original.

Let's start by using the formula for the perimeter of a triangle:

[tex]Perimeter of triangle ABC = AB + BC + AC = 65.5 feet[/tex]

We can also use Heron's formula to find the area of triangle ABC:

[tex]Area of triangle ABC = \sqrt(s(s-AB)(s-BC)(s-AC))[/tex]

where s is the semi perimeter of the triangle:

[tex]s = (AB + BC + AC) / 2[/tex]

We can use these equations to solve for the side lengths of triangle ABC:

[tex]AB + BC + AC = 65.5[/tex]

[tex]s = (AB + BC + AC) / 2[/tex]

[tex]25 = \sqrt(s(s-AB)(s-BC)(s-AC))[/tex]

Solving for AB, BC, and AC gives us:

AB = 15

BC = 20

AC = 30.5

Now, let's dilate triangle ABC by a factor of 5/2 to create triangle DEF. This means that each side of triangle ABC will be multiplied by 5/2 to get the corresponding side length of triangle DEF.

DE = AB * (5/2) = 37.5

EF = BC * (5/2) = 50

DF = AC * (5/2) = 76.25

Now we can use Heron's formula again to find the area of triangle DEF:

s = (DE + EF + DF) / 2 = 81.875

Area of triangle DEF = sqrt(s(s-DE) (s-EF) (s-DF)) = 312.5 square feet

To know more about triangle, visit:

https://brainly.com/question/2773823

#SPJ1

Answer:

x = √17

y = 10.1

Step-by-step explanation:

x² + 8² =  9²

x² = 81 - 64 = 17

x = √17

sin∅ = √17/9

∅ = 27.27°

9/y = cos(27.27)

y = 9/cos(27.27) = 10.13

y = 10.1

Sin 7π/4 is the value of sine trigonometric function for an angle equal to 7π/4 radians. The value of sin 7π/4 is -(1/√2) or -0.7071 (approx).

315° is comparable to 7 / 4 radians. In general, we multiply the angle measurement in radians by 180/ to translate an angle measurement given in radians to degrees. Therefore, we multiply 7 / 4 by 180 / to convert to radians. We discover that 7/4 radians equals 315 degrees.

We can first convert the angle to degrees as follows:

7π/4 radians = (7/4) × 180 degrees/π ≈ 315 degrees

The trigonometric ratios for 315 degrees (or 7/4 radians) can therefore be calculated using the reference angle of 45 degrees (which is /4 radians), as shown below.

sin(7π/4) = -sin(π/4) = -1/√2

cos(7π/4) = -cos(π/4) = -1/√2

tan(7π/4) = tan(π/4) = 1

csc(7π/4) = csc(-π/4) = -√2/2

sec(7π/4) = sec(-π/4) = -√2/2

cot(7π/4) = cot(-π/4) = 1

Therefore, the trigonometric ratios for the angle 7π/4 radians are:

sin(7π/4) = -1/√2

cos(7π/4) = -1/√2

tan(7π/4) = 1

csc(7π/4) = -√2/2

sec(7π/4) = -√2/2

cot(7π/4) = 1

To know more about trigonometric function visit:-

https://brainly.com/question/6904750

#SPJ1

The x⁶y³ term in the expansion will be:  35 x⁶y³.

The x⁸y² term in the expansion will be: 21x⁸y².

The binomial expansion of (x + y)ⁿ is given by the binomial theorem, which states:

(x + y)ⁿ = C(n, 0) * xⁿ * y⁰ + C(n, 1) * xⁿ⁻¹ * y¹ + C(n, 2) * xⁿ⁻² * y² + ... + C(n, k) * xⁿ⁻ᵏ * yᵏ + ... + C(n, n) * x⁰ * yⁿ

where;

Given that the term 210x⁴y⁶ appears in the expansion, we can infer that it corresponds to C(n, k) * x⁴ * y⁶, where k is the number of times y appears in the term, and (n - k) is the number of times x appears in the term.

Comparing this with the given term, we can deduce the values of n, k, and x in the following way:

C(n, k) = 210

x⁴ = x⁴

y⁶ = y³ * y³

Comparing the exponents on x and y, we can set up the following equations:

n - k = 4 (1)

k = 3 (2)

Solving equation (2) for k, we get:

k = 3

Substituting this value of k into equation (1), we can solve for n:

n - 3 = 4

n = 7

So, the value of n is 7.

Now, we can use the binomial coefficient formula to calculate C(n, k):

C(n, k) = C(7, 3) = 7! / (3! * (7 - 3)!) = 35

Finally, substituting the values of n, k, and C(n, k) into the general term of the expansion, we can find the specific terms:

The x⁶y³ term in the expansion will be:

C(7, 3) * x⁶ * y³ = 35 * x⁶ * y³

The x⁸y² term in the expansion will be:

C(7, 2) * x⁸ * y² = 21 * x⁸ * y²

Learn more about binomial expansion here: https://brainly.com/question/13602562

#SPJ1

After calculation we get

11) d. m/JML = 90 degrees, a. m/GMH = 45 degrees, b. mLH = 90 degrees, c. m/LKH = 45 degrees

12) a. AGKH is an isosceles triangle, b. Another triangle formed by two radii is an equilateral triangle.

13) a. m/GKH = 33.4 degrees, c. m/KHJ = 33.4 degrees, e. mJL66.8 degrees, b. m/KGH = 66.8 degrees, d. m/JKL = 113.2 degrees

A quadrilateral is a geometric shape with four straight sides and four angles. Examples of quadrilaterals include squares, rectangles, parallelograms, trapezoids, and kites.

According to the given information:

a. Since m/LGH and m/GHJ are both 45°, GH is a bisector of ∠JGL. Therefore, m/GMH = 90° - 45° = 45°.

b. Since GH is a bisector of ∠JGL, m/LGH = m/HGL = 45°. Also, since LH is a straight line, m/LGH + mLH + m/HGL = 180°. Thus, mLH = 90° - 45° = 45°.

c. Since GH is a bisector of ∠LJK, m/GHK = m/JHK = 45°. Also, since LK is a straight line, m/LKH + m/JHK + m/LJK = 180°. Thus, m/LKH = m/LJK = (180° - 2*45°)/2 = 45°.

d. Since GH is a bisector of ∠JGL and JML is a straight line, m/JML = m/JGH + m/HGL = 45° + 45° = 90°.

a. AGKH is a quadrilateral with two sides that are radii of the circle. Since all radii of a circle are equal, AGKH is a kite. Furthermore, since the two radii AG and KH are perpendicular to each other, AGKH is also a rectangle.

b. Another triangle formed by two radii is AKJ, where AK and AJ are radii of the circle and KJ is a chord.

a. Since GH is a diameter of the circle and GKH is a right triangle with ∠GHK = 90°, m/GKH = 180° - 90° = 90°.

b. Since GH is a diameter of the circle and KJ is a chord, m/KGH = m/KJ = 1/2 * m/KHJ = 1/2 * (180° - 113.2°) = 33.4°.

c. Since GH is a diameter of the circle and KHJ is a right triangle with ∠KHJ = 90°, m/KHJ = 180° - m/GKH = 180° - 90° = 90°.

d. Since GH is a diameter of the circle and JKL is a right triangle with ∠JKL = 90°, m/JKL = 180° - m/KJ - m/JKH = 180° - 33.4° - 45° = 101.6°.

e. Since JL is a chord of the circle and ∠JGL is an inscribed angle that intercepts it, m/JGL = 1/2 * m/JL = 1/2 * (180° - m/JKL) = 1/2 * (180° - 101.6°) = 39.2°. Also, since GH is a diameter of the circle and GJL is a right triangle with ∠GJL = 90°, m/GJL = 90° - m/GHL = 90° - 45° = 45°. Therefore, m/JLH = m/JGL - m/GLH = 39.2° - 45° = -5.8°. Note that the negative value indicates that ∠JLH is a reflex angle.

To know more about quadrilateral visit:

https://brainly.com/question/12431044

#SPJ1

This sentence relating to the quotient can be expressed mathematically as:

(30 / x) - 2

This sentence can be expressed mathematically as:

(30 / x) - 2

where x represents the unknown number.

The word "quotient" indicates that we are dividing 30 by the unknown number x. The phrase "is decreased by 2" means that we need to subtract 2 from the quotient.

Learn more about quotient  at:

https://brainly.com/question/16134410

#SPJ1

Answer:

B) 352

Step-by-step explanation:

45% = 0.45

640 x 0.45= 288

288 is how many students walked to school

So to find how many took the bus to school

640- 288= 352

In linear equation, 44%  of the shoppers have an e-mail account and 56%  of the shoppers do not have computer access at home.

What is a linear equation in mathematics?

A linear equation in algebra is one that only contains a constant and a first-order (direct) element, such as y = mx b, where m is the pitch and b is the y-intercept.

                         Sometimes the following is referred to as a "direct equation of two variables," where y and x are the variables. Direct equations are those in which all of the variables are powers of one. In one example with just one variable, layoff b = 0, where a and b are real numbers and x is the variable, is used.

Total number of the shoppers who were surveyed = 150

a). Number of shoppers who have an e-mail account = Shoppers who have email accounts and computer access at home + Shoppers who have email accounts but no computer access at home

= 44 + 22

= 66

Percentage of the shoppers having an e-mail account = 66/150 * 100

                                                                        = 44%

b). Total number of shoppers who do not have computer access at home

= 7 + 77

=  84

Percentage of the shoppers having computer access at home

                                             = 84/150  * 100   =  56%

Learn more about linear equation

brainly.com/question/11897796

#SPJ1

Answer:

The coins are picked without replacement.

The probability of picking at least one Canadian quarter is 1 minus the probability of picking 6 U.S. quarters:

[tex]1 - ( \frac{41}{50} )( \frac{40}{49} )( \frac{39}{48} )( \frac{38}{47} )( \frac{37}{46} )( \frac{36}{45} ) [/tex]

[tex] = 1 - .28296 = .71704[/tex]

So the probability of picking at least one Canadian quarter is about 71.7%.

The statement that (sin 2x) / (1 + cos 2x) = tan x can be proven.

To prove that (sin 2x) / (1 + cos 2x) = tan x, we will use trigonometric identities.

(sin 2x) / (1 + cos 2x)

(2sin x × cos x) / (1 + (cos²x - sin²x))

(2sin x × cos x) / (cos²x + 2sin x × cos x + sin²x)

We can rewrite the denominator using the Pythagorean identity sin²x + cos²x = 1:

(2sin x × cos x) / (1 + 2sin x × cos x)

(2sin x × cos x) × (1 - 2sin x × cos x) / (1 - (2sin x × cos x)²)

((2sin x × cos x) - (4sin²x × cos²x)) / (1 - 4sin²x × cos²x)

(2sin x - 4sin²x) / (1/cos²x - 4sin²x)

Since tan x = sin x / cos x, we can rewrite the expression:

(2tan x - 4tan²x) / (sec²x - 4tan²x)

(2tan x - 4tan²x) / (1 + tan²x - 4tan²x)

(2tan x - 4tan²x) / (1 - 3tan²x)

2tan x × (1 - 2tan²x) / (1 - 3tan²x)

tan x

So, we have proved that (sin 2x) / (1 + cos 2x) = tan x.

Find out more on proof at https://brainly.com/question/17029275

#SPJ1

Answer:

b)

Step-by-step explanation:

Answer:

step by step explanation:

All you have to do is expand and reduce the expressions

then evaluate -2 being a root of the expressions

To do that you need to substitute -2 into the simplified expressions

if the result comes as zero then f(-2) is factor of f(x) according to the factor theorem.

Example 1.

simplify (-5x-2)(7x-4)-2x+3

if you substitute f(x) as f(-2)

then substitute x with -2

when you simply and evaluate the expression you will get that the expression is equal to -137

which means -2 isn't a root since the expression must be equal to 0

-2 is not a root

do the same for the other expressions

The domain restrictions on the function [tex]\left f(x\right)=-\frac{3x}{81\:-\:x^2}\:\cdot \frac{81\:-\:x^2}{2x^2-6x}\:\div \frac{x^2+2x-6x}{3x^2-30x+63}[/tex] are the x values -9, 0, 3, 4 and 9

From the question, we have the following function that can be used in our computation:

[tex]\left f(x\right)=-\frac{3x}{81\:-\:x^2}\:\cdot \frac{81\:-\:x^2}{2x^2-6x}\:\div \frac{x^2+2x-6x}{3x^2-30x+63}[/tex]

Next, we set the denominator to 0 and solve for x

So, we have

81 - x²: x = ±9

2x² - 6x: x = 0 and x = 3

x² + 2x - 6x: x = 0 and x = 4

Hence, the domain restrictions are the x values -9, 0, 3, 4 and 9

Read more about domain at

https://brainly.com/question/2264373

#SPJ1

The numbers in each cell represent the frequency of people who chose that combination of gender and movie type.

What is the frequency?

The number of periods or cycles per second is called frequency. The SI unit for frequency is the hertz (Hz). One hertz is the same as one cycle per second.

To construct a two-way frequency table for the data, we need to organize the responses by gender and movie type. The table is in the attached image.

The rows represent the gender of the moviegoers, and the columns represent the movie type.

The numbers in each cell represent the frequency of moviegoers who chose that combination of gender and movie type.

For example, there are 12 men who chose Drama as their favorite movie type, and there are 13 women who chose Action as their favorite movie type.

The total number of moviegoers who chose Drama is 22, and the total number who chose Action is 27. The total number of moviegoers is 49.

Hence, The numbers in each cell represent the frequency of people who chose that combination of gender and movie type. For example, 12 men chose Drama as their favorite movie type.

To know more about the frequency visit:

https://brainly.com/question/5102661

#SPJ1

If the the a is greater than 1, compared to the parent function the C. Stretched vertically.

The equation y = ax^2 + c represents a quadratic function where "a" is the coefficient of the x^2 term and "c" is a constant term. The parent function of this quadratic function is y = x^2.

If the equation of a quadratic function is given in the form y = ax^2 + c and "a" is greater than 1, then the graph of the function will be stretched vertically and the vertex will be shifted up or down depending on the value of "c".

Find out more on parent functions at https://brainly.com/question/17079244

#SPJ1

The range of the function in the graph is  6≤e≤12. So correct option is A.

In mathematics, range is a term used to refer to the set of all possible output values of a function. It is the set of values that the function can take as its input varies over its entire domain. In other words, the range of a function is the set of all output values that can be obtained by evaluating the function for all possible input values.

For example, consider the function f(x) = x². The domain of this function is all real numbers, but the range is only non-negative real numbers, since x² is always non-negative for any real number x.

The range of a function can be determined by analyzing its graph, which is a visual representation of the function. The range corresponds to the set of all y-values that appear on the graph. For instance, the range of the function f(x) = sin(x) is the closed interval [-1, 1], since the sine function oscillates between -1 and 1 as its input varies over all real numbers.

Sometimes, it is useful to restrict the domain of a function in order to obtain a specific range. This process is called domain restriction or range selection. For example, the inverse function of f(x) = x² can be obtained by restricting the domain of f to non-negative real numbers, which ensures that the inverse function is also a function. The resulting function is f^-1(x) = √x, whose domain is non-negative real numbers and range is the same as the domain of f.

The range of the function in the graph is  6≤e≤12. So correct option is A.

To know more about function visit:

https://brainly.com/question/2709928

#SPJ1

So, multiple choice algebra questions. the correct answer would be option D: [tex]3x^7 - 6x^6 - 11x^4 + 4x^5 - 4x^2[/tex].

To simplify the given expression [tex](3x^4+4x^2) (x^3-2x^2-1)[/tex], we can use the distributive property of multiplication to multiply each term of the first expression by each term of the second expression. This gives us:

[tex](3x^4+4x^2) (x^3-2x^2-1) \\= 3x^4(x^3) + 3x^4(-2x^2) + 3x^4(-1) + 4x^2(x^3) - 4x^2(2x^2) - 4x^2(1)[/tex]

Simplifying each term, we get:

[tex]= 3x^7 - 6x^6 - 3x^4 + 4x^5 - 8x^4 - 4x^2[/tex]

So, the correct answer would be option D: [tex]3x^7 - 6x^6 - 11x^4 + 4x^5 - 4x^2.[/tex]

To know more about distributive property visit:

https://brainly.com/question/6276874

#SPJ1

The principal when making the first payment 51 months later on a private student loan with a principal of $10,000 and a rate of 12.59% would be $15,307.13.

To calculate the principal when making the first payment 51 months later on a private student loan with a principal of $10,000 and a rate of 12.59%, we first need to calculate the amount of interest that has accrued over the 51 months.

Using the formula:

Interest = Principal x Rate x Time

where Principal = $10,000,

Rate = 12.59% per year,

Time = 51/12 years (since the interest is compounded monthly):

Interest = $10,000 x 0.1259 x (51/12)

= $5,307.13

So the total amount owed after 51 months would be:

Total amount owed = Principal + Interest

= $10,000 + $5,307.13

= $15,307.13

Therefore, the principal when making the first payment 51 months later on a private student loan with a principal of $10,000 and a rate of 12.59% would be $15,307.13.

As for recent examples of community change that involves a clash between different cultures that helped disadvantaged communities and the populations, one example is the Black Lives Matter movement, which has brought attention to systemic racism and police brutality in the United States.  Another example is the #MeToo movement, which has raised awareness about sexual harassment and assault and has led to changes in workplace policies and cultural attitudes toward these issues.

Learn more about principal from

https://brainly.com/question/30163719

#SPJ1

0.685 is a decimal that equals 68.5%.

F(4)=9 is the value for this function.

A function that is defined by numerous smaller functions across various time intervals is known as a piecewise function. The domain of a function is the sum of all the smaller domains, and each sub-function has its own formula and domain. The input value and the function that establishes that interval determine the function's output.

The typical functional notation, which represents the body of a function as an array of functions and related subdomains, can be used to define piecewise functions. Together, these subdomains must encompass the entire domain; frequently, it is also necessary for them to be pairwise disjoint, or constitute a partition of the domain.

x=4 is bigger than or equal to 0 because it.

we use the third function definition

F(x)=x+5.

Therefore, F(4)=4+5=9.

To know more about function visit:

brainly.com/question/12431044

#SPJ1

There are 250 students in the sixth grade.

First, let's define some variables:

The total number of sixth-grade students is called "x."

The number of students who purchased their lunches will be referred to as "p."

The number of students who brought their lunch from home will be referred to as "h."

We know that from the problem statement that

p + h = x (since all students either purchased their lunch or brought their lunch from home)

p = 0.24x (since 24% of the students purchased their lunch)

h = 190 (since 190 students brought their lunch from home)

We can use these equations to solve for x:

p + h = x

0.24x + 190 = x (substituting in the value of p and h from the other equations)

0.76x = 190 (subtracting 0.24x from both sides)

x = 250 (dividing both sides by 0.76)

Therefore, there are 250 students in the sixth grade.

know more about percentage visit:

https://brainly.com/question/29306119

#SPJ1

Answer:

39 divided by 8 is equal to 4 with a remainder of 7.

The quotient is the number of times the divisor goes into the dividend. In this case, 8 goes into 39 4 times with a remainder of 7.

The remainder is the number that is left over after the divisor has been divided into the dividend. In this case, 7 is left over after 8 has been divided into 39.

Here is the long division of 39 by 8:

```

39 / 8

4

32

7

```

Step-by-step explanation:

The quotient of 39 divided by 8 is 4, and the remainder is 7.

We have,

When performing long division, we divide the dividend (39) by the divisor (8) to find the quotient and remainder.

  4

--------

8 | 39

  - 32

    ---

     7

Here's how the long division process works for 39 divided by 8:

-We start by dividing the first digit of the dividend (3) by the divisor (8). Since 3 is less than 8, we can't divide it evenly, so we move to the next digit (9).

- We now have 39 as the remaining portion of the dividend. We divide 39 by 8. The largest multiple of 8 that fits into 39 is 4. We place the quotient, which is 4, above the line.

- We multiply the quotient (4) by the divisor (8), which gives us 32. We subtract 32 from 39, which leaves us with a remainder of 7.

- Since there are no more digits to bring down from the dividend, and the remainder (7) is less than the divisor (8), we stop the division process.

Therefore,

The quotient of 39 divided by 8 is 4, and the remainder is 7.

Learn more about expressions here:

https://brainly.com/question/3118662

#SPJ6

For all x, P(x) (using universal quantifier ∀) and  It is not the case that there exists an x such that ~P(x) (using negation ¬ and existential quantifier ∃)

What is probability?

Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.

Let S be the set of students in your class and P(x) be the predicate "x has a cellular phone". Then, we can represent the statement "everyone in your class has a cellular phone" as:

1. For all x in S, P(x) (using universal quantifier ∀)

2. It is not the case that there exists an x in S such that ~P(x) (using negation ¬ and existential quantifier ∃)

If we want to represent the same statement for all people, we can use the same predicate P(x) and consider the domain of all people. Then, the statement "everyone has a cellular phone" can be represented as:

For all x, P(x) (using universal quantifier ∀)

It is not the case that there exists an x such that ~P(x) (using negation ¬ and existential quantifier ∃)Let S be the set of students in your class and P(x) be the predicate "x has a cellular phone". Then, we can represent the statement "everyone in your class has a cellular phone" as:

For all x in S, P(x) (using universal quantifier ∀)

It is not the case that there exists an x in S such that ~P(x) (using negation ¬ and existential quantifier ∃)

If we want to represent the same statement for all people, we can use the same predicate P(x) and consider the domain of all people. Then, the statement "everyone has a cellular phone" can be represented as:

1. For all x, P(x) (using universal quantifier ∀)

2. It is not the case that there exists an x such that ~P(x) (using negation ¬ and existential quantifier ∃)

To learn more about probability from the given link:

https://brainly.com/question/30034780

#SPJ1

if we change the value of 523 to 424 in the list of numbers, then the mean decreases by approximately 3.22 and the median stays the same.

How to calculate the mean?

To calculate the mean, we add up all the numbers in the list and divide by the total number of values. Before the change, the sum of the numbers is:

164 + 225 + 227 + 250 + 261 + 268 + 277 + 379 + 523 = 2494

And there are 9 numbers in the list. So the mean is:

2494 / 9 ≈ 277.11

If we change the value of 523 to 424, then the sum becomes:

164 + 225 + 227 + 250 + 261 + 268 + 277 + 379 + 424 = 2465

And there are still 9 numbers in the list. So the new mean is:

2465 / 9 ≈ 273.89

So the mean decreases by approximately 3.22.

To calculate the median, we find the middle value of the list. If the list has an odd number of values, then the median is the middle value. If the list has an even number of values, then the median is the average of the two middle values. In this case, the list has an odd number of values, so the median is:

261

If we change the value of 523 to 424, then the list becomes:

164, 225, 227, 250, 261, 268, 277, 379, 424

And the median is still:

261

So the median stays the same.

In summary, if we change the value of 523 to 424 in the list of numbers, then the mean decreases by approximately 3.22 and the median stays the same.

To know more about mean visit :-

https://brainly.com/question/26177250

#SPJ1

Answer:

B is the answer

Step-by-step explanation:

The expression that is not equal to the others is B [[2/−5]] The other expressions are A −[[2/5]], C [[−2/5]], and D [[2/5]].

Answer: Option A:

To calculate the total amount Owen will spend on Option A, we need to calculate the monthly payment and then multiply it by the number of months:

First, we need to calculate the total amount of the loan. Owen is making a down payment of $3200, so he will be borrowing $28,820 (the price of the car minus the down payment).

Next, we can use the formula for calculating the monthly payment for a loan:

P = (r * A) / (1 - (1 + r)^(-n))

where P is the monthly payment, r is the monthly interest rate, A is the total amount of the loan, and n is the number of months.

For Option A, the monthly interest rate is 1.3% / 12 = 0.01083, the total amount of the loan is $28,820, and the number of months is 36. Plugging these values into the formula, we get:

P = (0.01083 * 28,820) / (1 - (1 + 0.01083)^(-36)) = $860.45

Therefore, the total amount Owen will spend on Option A is:

36 * $860.45 = $30,975.98

Option B:

For Option B, we need to take into account the $1500 cash back that Owen will receive as part of the down payment. This means that the total amount of the loan will be $32,020 - $3200 - $1500 = $27,320.

To calculate the monthly payment, we can use the same formula as before:

P = (r * A) / (1 - (1 + r)^(-n))

For Option B, the monthly interest rate is 5.2% / 12 = 0.04333, the total amount of the loan is $27,320, and the number of months is 36. Plugging these values into the formula, we get:

P = (0.04333 * 27,320) / (1 - (1 + 0.04333)^(-36)) = $825.53

Therefore, the total amount Owen will spend on Option B is:

36 * $825.53 + $1500 = $30,316.08

Therefore, Option A will cost Owen a total of $30,975.98, and Option B will cost him a total of $30,316.08. Therefore, Option B is the cheaper option for Owen.

Step-by-step explanation: