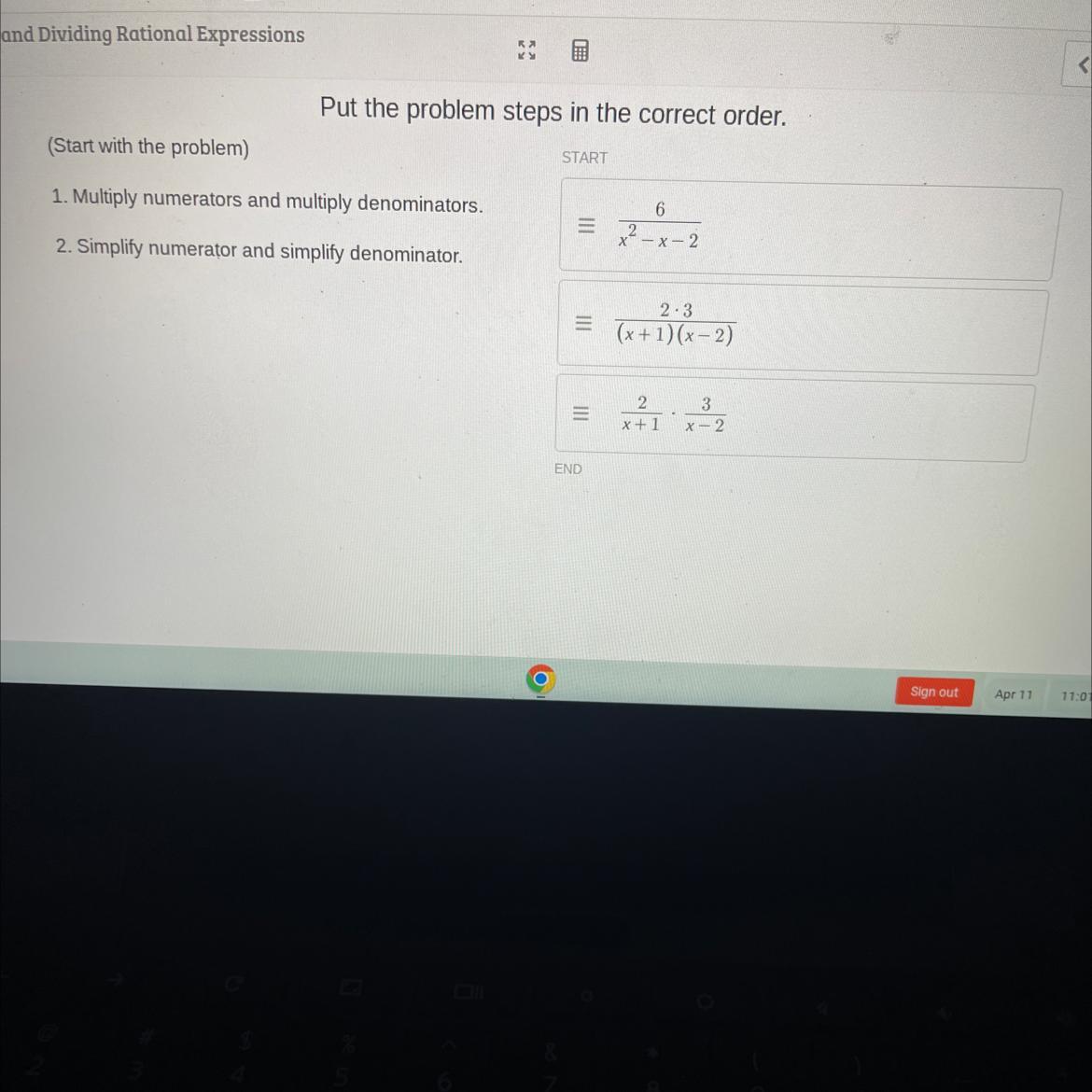
Answers
The problem steps should be put in the correct order as follows;
Problem ≡ [tex]\frac{2}{x+1} \cdot \frac{3}{x-2}[/tex]
Multiply numerators and multiply denominators ≡ [tex]\frac{2 \cdot 3}{(x+1)(x-2)}[/tex]
Simplify numerator and Simplify denominator ≡ [tex]\frac{6}{(x^2 - x - 2)}[/tex]
What is a fraction?In Mathematics and Geometry, a fraction simply refers to a numerical quantity (numeral) which is not expressed as a whole number. This ultimately implies that, a fraction is simply a part of a whole number.
What is a rational expression?In Mathematics and Geometry, a rational expression simply refers to a type of expression which is expressed as a fraction. In this exercise, we would factorize the numerator and denominator for this rational expression as follows;
Multiply numerators = 2 × 3 = 6
Multiply denominators = (x + 1) × (x - 2) = x² - 2x + x - 2 = x² - x - 2
In conclusion, the required rational expression is given by [tex]\frac{6}{(x^2 - x - 2)}[/tex]
Read more on fraction here: brainly.com/question/29367657
#SPJ1
Related Questions
please help it’s a review question but i don’t get it
Answers
Possible translations such that the graph passes through the point (1,2) are given as follows:
Translate the graph one unit right and one unit up.Translate the graph three units right and two units down.What is a translation?A translation happens when either a figure or a function is moved horizontally or vertically on the coordinate plane.
The four translation rules for functions are defined as follows:
Translation left a units: f(x + a).Translation right a units: f(x - a).Translation up a units: f(x) + a.Translation down a units: f(x) - a.Two possible translations for the function to pass through the point (1,2) are given as follows:
Translate the graph one unit right and one unit up, considering that the function passes through the point (0, 1), hence x + 1, y + 1.Translate the graph three units right and two units down, considering that the function passes through the point (-2, 4).More can be learned about translations at brainly.com/question/28174785
#SPJ1
for which data frequency is seasonality not a problem? group of answer choices monthly. weekly. annual. daily. quarterly.
Answers
Seasonality may be less of a problem for annual data frequency as there may be less variation due to the longer time interval.
What is annual data frequency?Annual data frequency refers to data that is collected and reported on an annual basis. This means that the data points in the dataset represent a full year's worth of data, with one data point for each year. Annual data is often used in economic indicators, such as gross domestic product (GDP) or unemployment rates, and can provide insights into long-term trends and changes over time.
What is GDP?GDP stands for Gross Domestic Product, which is a measure of the total value of goods and services produced within a country's borders during a specific time period, typically a year. It is used as an indicator of a country's economic health and growth. GDP is calculated by adding up the total spending on consumption, investment, government spending, and net exports (exports minus imports) during the period.
According to the given informationSeasonality may still be a problem for data frequencies of monthly, weekly, daily, and quarterly as certain patterns or fluctuations may occur within each of these time intervals. Seasonality may be less of a problem for annual data frequency as there may be less variation due to the longer time interval.
To know more about the GDP visit:
brainly.com/question/15899184
#SPJ1
your friend is binging half of a crate of popsicles to the picnic. of you put what is left in the crate evenly into 6 ice buckets, what fraction of the crate will go into each of ice bucket
Answers
Thus, the fraction of crate that will go in each of the ice bucket is found as - 1/12.
Explain about the fraction:An element of a whole is a fraction. The number is represented mathematically as a quotient, where the numerator and denominator are split. Both are integers in a simple fraction. A fraction appears in the numerator or denominator of a complex fraction.
Fractions with a numerator less than the denominator are said to be proper fractions. When the numerator exceeds the denominator, the fraction is said to be inappropriate.
Given data:
fraction of crate brought by friend = 1/2
Total number of ice buckets = 6
Fraction of crate in each bucket = fraction of crate brought by friend / Total number of ice buckets
Fraction of crate in each bucket = (1/2) / 6
Fraction of crate in each bucket = 1 / (2*6)
Fraction of crate in each bucket = 1/12
Thus, the fraction of crate that will go in each of the ice bucket is found as - 1/12.
know more about the fraction:
https://brainly.com/question/78672
#SPJ1
This is for the unit 4 lesson 7 Triangles Unit Test please help. Identify the combination of angle measures that could form a triangle
Answers
The combination of angle measures that could form a triangle are (a) 22, 140, 18 degrees and (c) 55, 67, 58 degrees.
In a triangle, the sum of the three interior angles is always equal to 180 degrees. Therefore, if the sum of the given angle measures is equal to 180 degrees, they could form a triangle.
For option a) 22 + 140 + 18 = 180, so the given angles could form a triangle.
For option b) 72 + 92 + 46 = 210, which is greater than 180, so the given angles could not form a triangle.
For option c) 55 + 67 + 58 = 180, so the given angles could form a triangle.
Therefore, the correct options are (a) 22,140,18 degrees and (c) 55,67,58 degrees
Learn more about triangle here
brainly.com/question/14611583
#SPJ4
The given question is incomplete, the complete question is:
Identify the combination of angle measures that could form a triangle
a) 22,140,18 degrees
b) 72,92,46 degrees
c) 55,67,58 degrees
One computer can process a payroll in 6 hours a new computer can do it in 4 hour how long would it take both computers together
Answers
Both computers working together can process the payroll in 2.4 hours.
Let's denote the time it takes for both computers working together to process the payroll as "t".
We can use the formula:
work done = rate x time
where "work done" is the same in both cases, as they are processing the same payroll. Therefore, we can set up an equation using the rates :
1/6 + 1/4 = 1/t
We can simplify the left-hand side of the equation:
2/12 + 3/12 = 1/t
5/12 = 1/t
Multiplying both sides by 12t:
5t = 12
t = 12/5
t = 2.4
To know more about work done, here
brainly.com/question/13662169
#SPJ4
Graph the equation y=x2+4x-5 on the accompanying set of axes. You must plot 5 points including the roots and the vertex.
Answers
Answer:
Roots = (1, 0) and (-5, 0)
Vertex = (-2, -9)
Two additional points = (-4, -5) and (0, -5)
Step-by-step explanation:
The given equation y = x² + 4x - 5 is a quadratic equation with a positive leading coefficient. Therefore, the shape of the curve is a parabola that opens upwards.
The roots of a quadratic equation are the x-values that satisfy the equation y = 0. They are the points at which the curve crosses the x-axis.
To calculate the roots of the given equation, set it to zero and solve for x.
[tex]\begin{aligned}x^2+4x-5&=0\\x^2+5x-x-5&=0\\x(x+5)-1(x+5)&=0\\(x-1)(x+5)&=0\\\\\implies x-1&=0 \implies x=1\\\implies x+5&=0 \implies x=-5\end{aligned}[/tex]
Therefore, the roots of the equation are (1, 0) and (-5, 0).
The x-value of the vertex of a quadratic function in the form ax² + bx + c is -b/2a.
For the given equation y = x² + 4x - 5, a = 1 and b = 4.
To find the x-value of the vertex, substitute these values into the formula:
[tex]x_{\sf vertex}=\dfrac{-b}{2a}=\dfrac{-4}{2(1)}=-2[/tex]
To find the y-value of the vertex, substitute the x-value of the vertex into the given equation:
[tex]y_{\sf vertex}=(-2)^2+4(-2)-5=-9[/tex]
Therefore, the vertex is (-2, -9).
To find two other points on the curve, substitute two values of x into the equation.
[tex]\begin{aligned}x=-4 \implies y&=(-4)^2+4(-4)-5\\&=16-16-5\\&=0-5\\&=-5\end{aligned}[/tex]
[tex]\begin{aligned}x=0 \implies y&=(0)^2+4(0)-5\\&=0+0-5\\&=0-5\\&=-5\end{aligned}[/tex]
The axis of symmetry of a quadratic equation is the vertical line that divides the parabola into two mirror images. The x-value of the vertex is the axis of symmetry. Therefore, the axis of symmetry is x = -2.
To graph the given equation:
Plot the roots (1, 0) and (-5, 0).Plot the vertex (-2, -9).Plot two additional points (-4, -5) and (0, -5).Draw the axis of symmetry x = -2.Draw a parabola that is symmetrical about the axis of symmetry and passes through the plotted points.Determine whether the given set S is a subspace of the vector space V. Note: Pn(R) is the vector space of all real polynomials of degree at most n and Mn(R) is the vector space of all real n x n matrices = OA. V is the vector space of all real-valued functions defined on the interval [a, b], and S is the subset of V consisting of those functions satisfying f(a) = f(b). B. V = P5(R), and S is the subset of V P5(R) consisting of those polynomials satisfying p(1) > p(0). C. V = C3(1), and S is the subset of V consisting of those functions satisfying the differential equation y'" + 2y = x2. D. V = Mn(R), and S is the subset of all skew-symmetric matrices. VE. V = C2(I), and S is the subset of V consisting of those functions satisfying the differential equation y" – 4y' + 3y = 0. F. V = R", and S is the set of solutions to the homogeneous linear system Ax = 0 where A is a fixed m X n matrix. OG. V = R", and S is the set of vectors (x1 , X2, X3 ) in V satisfying x1 – 4x2 + x3 = 3
Answers
S is a subspace of the vector space V.
For four conditions are satisfied,
The set S is a subspace of C3(1)
The set S is a subspace of Mn(R)
The set S is a subspace of C2(I)
The set S is a subspace of [tex]R^n[/tex]
The set S is not a subspace of P5(R) because it is not closed under scalar multiplication.
If p(x) is a polynomial in S, then 2p(x) may not satisfy the condition. [tex]p(1) > p(0).[/tex]
The set S is a subspace of C3(1).
The differential equation [tex]y\prime\prime\prime + 2y = x^2[/tex] is linear and homogeneous, so the sum of two solutions is also a solution, and a constant multiple of a solution is also a solution.
S is closed under linear combinations.
The set S is a subspace of Mn(R) because it is closed under addition and scalar multiplication.
If A and B are skew-symmetric matrices, then[tex](A + B)^T = A^T + B^T = -A - B = -(A + B), so A + B[/tex]is skew-symmetric. Similarly, if c is a scalar, then [tex](cA)^T = cA^T = -cA, so c A[/tex] is skew-symmetric.
S is a subspace of C2(I) because it is closed under addition and scalar multiplication.
If y1 and y2 are solutions to[tex]y\prime\prime - 4y\prime+ 3y = 0, then y1\prime\prime - 4y\prime + 3y1 = 0[/tex] and [tex]y2\prime\prime - 4y2\prime + 3y2 = 0[/tex].
Adding these equations gives [tex](y1 + y2)\prime\prime - 4(y1 + y2)\prime + 3(y1 + y2) = 0,[/tex] so [tex]y1 + y2[/tex]is also a solution.
Similarly, if c is a scalar, then [tex](cy)\prime\prime - 4(cy)\prime + 3(cy) = c(y\prime\prime - 4y\prime+ 3y) = 0[/tex], so cy is also a solution.
The set S is a subspace of [tex]R^n[/tex]because it is the null space of a fixed matrix A.
The null space of a matrix is always closed under addition and scalar multiplication.
The set S is not a subspace of [tex]R^n[/tex]because it is not closed under addition. If (1, 1, 0) and (0, 2, 1) are in S, then their sum (1, 3, 1) is not in S because. [tex]1 - 4(3) + 1 \neq 3.[/tex]
For similar questions on Subspace
https://brainly.com/question/13045843
#SPJ11
I will be given brainliest!!!!
Answers
Answer:2/3
Step-by-step explanation:
its the only possible answer because it needs to have a scale factor below one as A'B'C'D' is smaller than ABCD
Answer: 2/3
Step-by-step explanation:
The corresponding side of AD is A'D'.
AD = 30
A'D' = 20
Scale factor = 2/3 because AD * 2/3 = A'D'
If I'm wrong, please tell me.
perform the operation form the sum 3a^2-ab-2b^2 and 2a^2 +5ab "-3b^2." subtract a^2 "-3ab-4b^2" i searched up it wont work but help me please
Answers
The result of the operation 3a²-ab-2b² and 2a² +5ab "-3b² is
4a² + 7ab - b².
What is an algebraic expression?
An algebraic expression is a mathematical phrase that contains variables, constants, and mathematical operations. It may also include exponents and/or roots. Algebraic expressions are used to represent quantities and relationships between quantities in mathematical situations, often in the context of problem-solving.
Let's simplify the expressions and then perform the given operation:
3a² - ab - 2b² + 2a² + 5ab - 3b² - (a² - 3ab - 4b²)
Combining like terms within parentheses:
3a² - ab - 2b² + 2a² + 5ab - 3b² - a² + 3ab + 4b²
Combining like terms outside parentheses:
4a² + 7ab - b²
Therefore, the result of the operation is 4a² + 7ab - b².
To learn more about algebraic expression from given link:
https://brainly.com/question/19245500
#SPJ1
find the volume of a cylinder with a diameter of 16 mi and a height of 5 mi
Answers
Answer: 320π or approximately 1005.31 mi
Step-by-step explanation:
The formula for the volume of a cylinder is
π r² h
we need to find the radius which is 16/2 = 8
plug in and solve
π 8² *5
π 64 *5
320π or approximately 1005.31 mi
Please help Thank you
Answers
The values of trigonometric-ratios in the given triangle whose legs are 4 and [tex]4\sqrt{3}[/tex] are:
a)sinθ=0.5
b)cosθ=0.866
c)tanθ=0.577
What is trigonometric-ratios ?
A right angle triangle has six trigonometric ratios: Sin, Cos, Tan, Cosec, Sec, and Cot. Sine, Cosine, Tangent, Cosecant, Secant, and Cotangent are their respective acronyms. These ratios show the ratio of various sides depending on the angle selected.
Given sides of triangle: 4 and [tex]4\sqrt{3}[/tex]
hypotenuse=[tex]\sqrt{perpendicular^{2}+base^{2} }[/tex]
=[tex]\sqrt{4^{2}+\((4\sqrt{3}) ^{2} }[/tex]
=[tex]\sqrt{16+48}[/tex]
=8
a)Sin θ=[tex]\frac{side opposite to the given angle}{hypotenuse}[/tex]
Sin θ=[tex]\frac{4 }{8}[/tex]
Sin θ=[tex]\frac{1}{2}[/tex]
Sin θ=0.5
b)Cos θ=[tex]\frac{side adjacent to the given angle}{hypotenuse}[/tex]
=[tex]\frac{4\sqrt{3} }{8}[/tex]
=[tex]\frac{\sqrt{3} }{2}[/tex]
=[tex]\frac{1.732}{2}[/tex]
Cos θ=0.866
c)tan θ=[tex]\frac{side opposite to the given angle}{side adjacent to the given angle}[/tex]
=[tex]\frac{4}{4\sqrt{3} }[/tex]
=[tex]\frac{1}{\sqrt{3} }[/tex]
tan θ=0.577
To know more about trigonometric-ratios, visit:
https://brainly.com/question/25122825
#SPJ1
a doctor can complete 3 examinations in 2 hours. how many examinations can the doctor complete in 4 hours? hint: use the proportion 3 exams : 2 hours :: x exams : 4 hours. 5 exams 5 exams 6 exams 6 exams 7 exams 7 exams 8 exams
Answers
Answer:
6 examinations
Step-by-step explanation:
We Know
A doctor can complete 3 examinations in 2 hours.
How many examinations can the doctor complete in 4 hours?
We see
4 hours is 2 hours times 2
We take
3 x 2 = 6 examinations
So, the doctor can complete 6 exams in 4 hours.
which expressions are equivalent to 8 13 ?
Answers
The next four equivalent fractions of 8/13 are:
16/2624/3932/5240/65What are some equivalent fractions of 8/13?Equivalent fractions are fractions that represent the same value but have different numerator and denominator. To find equivalent fractions of 8/13, we can multiply both the numerator and the denominator by the same non-zero integer.
In this case, we multiplied the numerator and denominator by 2, 3, 4, and 5, respectively, to obtain the next four equivalent fractions: 16/26, 24/39, 32/52, and 40/65. These fractions have different numerators and denominators, but they are equivalent to 8/13 as they represent the same value or amount.
Read more about equivalent expression
brainly.com/question/15775046
#SPJ1
Solve for length of segment d.
= 4 cm
b = 12 cm
c = 6 cm
4. ? =
].d
Enter the segment length tha
belongs in the green box.
If two segments intersect inside
or outside a circle: ab = cd
Answers
Answer: Using the given information and the formula ab = cd, we can write:
d = (ab) / c
We are given b = 12 cm and c = 6 cm. To find ab, we can use the Pythagorean theorem:
a^2 + b^2 = c^2
where a is the unknown length we want to find. Substituting the given values, we get:
a^2 + 12^2 = 6^2
a^2 + 144 = 36
a^2 = -108 (which is not a possible solution)
This means that the given values do not form a valid triangle. Therefore, we cannot find the length of segment d using the given information.
Step-by-step explanation:
Jessica wants to add a border around the edge of the solar panels to help protect them from weather events. Write the standard form expression that represents the amount of border material Jessica will need. Enter the correct answer in the box.
answer : 8c^2 + 24c - 6
Answers
The standard form expression that represents the amount of border material Jessica will need is 2L + 2W - 2x - 2y = -2B
To create this expression, we need to consider a few things. Firstly, we need to know the length and width of the solar panels. Let's say the length of the solar panel is L and the width is W. We also need to know the width of the border that Jessica wants to add. Let's call this value B.
The total amount of material needed for the border will be the sum of the material needed for the four sides of the solar panel. Each side will need a length of B, so the total length of the material needed will be 2B + 2L + 2W.
However, we can simplify this expression by putting it into standard form. Standard form expressions are written in a specific way that makes them easier to read and work with. In standard form, the expression is written as Ax + By = C, where A, B, and C are constants and x and y are variables.
To put the expression 2B + 2L + 2W into standard form, we need to group the variables together and move the constants to the other side of the equation. This gives us the expression 2L + 2W - Ax - By = -2B, where A and B are both equal to -2, and C is equal to -2B.
To know more about expression here
https://brainly.com/question/14083225
#SPJ4
Answer:
8c^2 + 24c - 6
Step-by-step explanation:
I got it right on edmentum
find the measurement of angle A and round the answer to the nearest tenth.
(Show work if you can plsss).
Answers
Answer:
40.8°
Step-by-step explanation:
SohCahToa
use tan
tan^-1(19/22)
=40.81508387
=40.8
Answer:
Step-by-step explanation:
Here,
Opposite side is 19
Adjacent side is 22
To find : The value of Angle A, that is X°.
Formula
Tan X° = Opposite side/Adjacent side
Tan X° = 19/22 = 0.863 ( approximately )
X° = Tan inverse (0.863)
X° = 40.79° ~ 40.8°
Rounding off this to nearest tenth is 41°.
Hence,
X° = 41°
That is,
Angle A is 45°.
Which of the following phrases can be used to represent -11?
the opposite of -11
eleven greater than zero
eleven below zero
positive eleven
Thx
Answers
Answer:
Eleven below Zero
Step-by-step explanation:
Every number below zero (less than zero) is a negative number.
plsss answer i'll give 50
Answers
Step-by-step explanation:
I know it not all but this is what I have
Solve x^2 + 6x + 9 = 0 by graphing. Please enter the number part of your answer only.
If your answer has two numbers, enter them like this: x = 6 and -1 should be entered as "6, -1" (no quotes).
Answers
Answer:
-3
Step-by-step explanation:
You want the graphical solution to x² +6x +9 = 0.
GraphThe graph of the expression on the left shows it has a value of 0 when x = -3.
The solution is x = -3.
__
Additional comment
A graphing calculator is very helpful when you want a graphical solution.
If you want to graph this by hand, you can rewrite it as ...
(x +3)² = 0
The graph of (x +3)² is a graph of the parent function y = x² after it has been shifted left 3 units. The graph will go through points (-5, 4), (-4, 1), (-3, 0), (-2, 1), (-1, 4). Of course the point at (-3, 0) indicates the solution is x=-3.
we wish to estimate the proportion of all college students who are working while going to school to within 4% at the 90% confidence level. we believe the true proportion is around 40%. how large a sample should we take to get the desired accuracy?
Answers
To estimate the sample size required for estimating the proportion of college students who are working while going to school with a desired accuracy of 4% at a 90% confidence level, we can use the following formula:
n = (Z^2 * p * (1-p)) / (E^2)
where:
n is the sample size
Z is the Z-score corresponding to the desired confidence level (90% confidence level corresponds to a Z-score of 1.645)
p is the estimated proportion (or expected proportion) of the population
E is the desired margin of error
Given:
Desired accuracy (E): 4% or 0.04
Confidence level (Z-score): 1.645 (corresponding to 90% confidence level)
Estimated proportion (p): 0.40 (or 40%)
Plugging the values into the formula, we get:
n = (1.645^2 * 0.40 * (1-0.40)) / (0.04^2)
n = 0.1239 / 0.0016
n ≈ 77.4375
Rounding up to the nearest whole number, the estimated sample size required to achieve the desired accuracy is 78.
So, a sample size of at least 78 college students would be needed to estimate the proportion of college students who are working while going to school with a margin of error of 4% at a 90% confidence level, assuming an estimated proportion of 40%.
Lin plans to swim 12 laps in the pool. She has swum 9.75 laps so far.
How many laps does she have left to swim? Use y
for the number of laps that Lin has left to swim.
Answers
Lin plans to swim 12 laps and has already swum 9.75 laps, so the number of laps she has left to swim can be found by subtracting 9.75 from 12:
y = 12 - 9.75
Simplifying the right side:
y = 2.25
Therefore, Lin has 2.25 laps left to swim.
2. There are 80 girls in the sophomore class of 200 students. Find the ratio of girls to non-girls.
Answers
Answer: 2 girls to 3 non-girls
Step-by-step explanation:
80 are girls
120 are boys (200-80)
80:120
simplify
2:3
There are 549 coins in a bottle.
ſ of the coins are £1 coins.
164 of the coins are 50p coins.
The rest of the coins are 20p coins.
Work out the total value of the 549 coins in pounds (£).
+
Total marks: 4
Answers
The total value of the 549 coins in pounds (£) is £378.20 (or £379), depending on whether there are 110 or 111 20p coins.
Let's start by finding the number of £1 coins in the bottle. We know that ſ (one-half) of the coins are £1 coins, so:
ſ × 549 = 1/2 × 549 = 274.50
Since we can't have half a coin, we know that there are either 274 or 275 £1 coins in the bottle.
Next, we know that there are 164 50p coins in the bottle.
To find the number of 20p coins, we can subtract the number of £1 and 50p coins from the total number of coins:
549 - 274 (or 275) - 164 = 111 (or 110)
So, there are either 110 or 111 20p coins in the bottle.
To calculate the total value of the coins, we can multiply the number of each type of coin by its value and then add them up:
Value of £1 coins = £1 × 274 (or 275) = £274 (or £275)
Value of 50p coins = £0.50 × 164 = £82
Value of 20p coins = £0.20 × 111 (or 110) = £22.20 (or £22)
Total value = £274 (or £275) + £82 + £22.20 (or £22) = £378.20 (or £379)
Therefore, the total value of the 549 coins in pounds (£) is £378.20 (or £379), depending on whether there are 110 or 111 20p coins.
To know more about coins
https://brainly.com/question/29869268
#SPJ4
The function y =30+5x represents the cost y (in dollars) of having your dog groomed and buying x for extra services. Sorry my mind is numb I have had a butt ton of work cut out for me.
Answers
Yes, the situation is a linear function as y = 30 + 5x is representing the standard form of a linear equation y = mx + b where m is the slope and b is the y-intercept.
Function is equal to ,
y = 30 + 5x
General form of the linear function is written as
y = mx + b
Here, the slope of the equation is 5,
This implies that for every additional service bought the cost increases by $5.
The y-intercept of the equation is 30.
This represents the initial cost of getting the dog groomed without any additional services.
The graph of this function will be a straight line.
And the relationship between the cost and the number of extra services bought will be linear.
When the number of extra services bought increases the cost of grooming the dog will increase by a constant amount .
Here the constant amount is equals to $5 per service.
Therefore, the function y = 30 + 5x is representing a linear function with slope 5 and y-intercept 30.
Learn more about linear function here
brainly.com/question/25058754
#SPJ4
The above question is incomplete, the complete question is:
The function y =30+5x represents the cost y (in dollars) of having your dog groomed and buying x extra services. Does this situation represent a linear function? Explain
Find the number of possibilities in each scenario
Find the number of ways 4 members from a family’s of 5 can line up for a photo shoot
Answers
There are [tex]5[/tex] ways to choose 4 members from a family of 5 to line up for a photo shoot.
What is the number of possibilities?The problem you are describing is a classic example of a combination problem, specifically choosing a certain number of items from a larger set without regard to the order in which they are arranged.
The formula to calculate the number of ways to choose "r" items from a set of "n" items without replacement is given by the combination formula, also known as "n choose r" or denoted as C(n, r). The formula is:
[tex]C(n, r) = n! / (r! \times (n - r)!)[/tex]
where "!" denotes the factorial of a number, which is the product of all positive integers up to that number.
In your case, you are choosing 4 members from a family of 5 for a photo shoot, and the order in which they line up does not matter. So you need to find C(5, 4).
Plugging the values into the formula:
[tex]C(5, 4) = 5! / (4! \times (5 - 4)!) = 5! / (4! \times 1!) = (5 \times 4 \times 3 \times 2 \times 1) / ((4 \times 3 \times 2 \times 1) \times 1) = 5[/tex]
Therefore, there are [tex]5[/tex] ways to choose 4 members from a family of 5 to line up for a photo shoot.
Learn more about possibilities here:
https://brainly.com/question/21366488
#SPJ1
g fit the logistic regression model to predict diabetic status based on age and glucose levels. what is the odds of ratio of being diabetic for older adults compared to adults while controlling for glucose levels? round your answer to 0.01.
Answers
To calculate the odds ratio of being diabetic for older adults compared to adults while controlling for glucose levels in a logistic regression model, we exponentiate the coefficient estimate for Age. For example, if the estimate is 0.05, the odds ratio is 1.65.
To obtain the odds ratio for older adults compared to adults while controlling for glucose levels in a logistic regression model predicting diabetic status based on age and glucose levels, we would need to look at the coefficient estimate for the age variable. Let's say the logistic regression model is
logit(P(Diabetic)) = β_0 + β_1Age + β_2Glucose
where P(Diabetic) is the probability of being diabetic, Age is the age in years, and Glucose is the glucose level in mg/dL. β_1 represents the coefficient estimate for Age.
To calculate the odds ratio for older adults (e.g., those who are 10 years older than the average age in the sample) compared to adults while controlling for glucose levels, we can exponentiate the coefficient estimate for Age and round to 0.01. That is
OR = exp(β_1*10)
For example, if the coefficient estimate for Age is 0.05, then:
OR = exp(0.05*10) = 1.65
This means that for every 10-year increase in age, the odds of being diabetic compared to non-diabetic increase by a factor of 1.65 while holding glucose levels constant.
To know more about logistic regression model:
https://brainly.com/question/30439764
#SPJ4
The arrival times of vehicles at the ticket gate of a sports stadium may be assumed to be poisson with a mean of 25 veh/hr. It takes an average of 1. 5 min for the necessary tickets to be bought for occupants of each car. (a)what is the expected length of queue at the ticket gate, not including the vehicle being served? (b)what is the probability that there are no more than 5 cars at the gate, including the vehicle being served? (c)what will be the average waiting time of a vehicle?
Answers
(a) The expected length of the queue, not including the vehicle being served, is 0.625 vehicles.
(b) The probability that there are no more than 5 cars at the gate, including the vehicle being served, is approximately 0.0176.
(c) The average waiting time of a vehicle at the ticket gate is 1.5 minutes or 0.025 hours.
(a) To find the expected length of the queue at the ticket gate, we need to calculate the expected number of vehicles waiting in the queue at any given time. This can be found by using the Little's Law, which states that the expected number of customers in a stable system is equal to the arrival rate multiplied by the average time spent in the system.
In this case, the arrival rate is 25 vehicles per hour, and the average time spent in the system is the time it takes to buy the tickets, which is 1.5 minutes or 0.025 hours. Therefore, the expected number of vehicles waiting in the queue is
E[N] = λW = 25 x 0.025 = 0.625 vehicles
So the expected length of the queue, not including the vehicle being served, is 0.625 vehicles.
(b) To find the probability that there are no more than 5 cars at the gate, including the vehicle being served, we need to use the Poisson distribution with a mean of 25 vehicles per hour. Let X be the number of vehicles arriving in an hour, then X Poisson(25).
P(X ≤ 5) = ∑ P(X = k) for k = 0 to 5
= ∑ (e^(-λ) × λ^k / k!) for k = 0 to 5
= e^(-25) × (25^0 / 0!) + e^(-25) × (25^1 / 1!) + ... + e^(-25) × (25^5 / 5!)
Using a calculator or software, this probability is found to be approximately 0.0176.
(c) The average waiting time of a vehicle can be found by dividing the expected number of vehicles waiting in the queue by the arrival rate. From part (a), we know that the expected number of vehicles waiting in the queue is 0.625 vehicles. The arrival rate is 25 vehicles per hour. Therefore, the average waiting time of a vehicle is
W = E[N] / λ = 0.625 / 25 = 0.025 hours or 1.5 minutes
So the average waiting time for a vehicle at the ticket gate is 1.5 minutes.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
A bookstore had 90 copies of a magazine. Yesterday, it sold 1/6 of them. Today, it sold 2/5 of the remaining copies. How many copies does the bookstore still have
Answers
Therefore , the solution of the given problem of unitary method comes out to be 45 copies of the magazine are still available at the bookstore.
Definition of a unitary method.Use the tried-and-true core approach, the real variables, nor any useful information you learn from the general and detailed questions to finish the project expression. Customers may be given another chance to taste the products in response. If these improvements don't happen, we'll miss out on significant advancements in programming comprehension.
Here,
Let's figure out how many issues of the magazine are still available in the store.
Given: There were 90 copies in all when the bookstore opened.
1/6 of the total copies were sold at the bookstore yesterday.
=> 15 copies were sold yesterday = (1/6) * 90.
=> Total copies - Copies sold yesterday = 90 - 15 = 75 Remaining copies after yesterday's sale
=> 2/5 of the remaining copies were sold in the bookstore today.
30 copies were sold today, which
=> (2/5) * 75.
The quantity of copies left after today's sale equals the quantity left after yesterday's sale. - Today's sales of copies:
=> 75 - 30 = 45
45 copies of the magazine are still available at the bookstore.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
The average age in a sample of 90 students at City College is 20. As a result of this sample, it can be concluded that the average age of all the students at City College:
Answers
If the sample is not truly representative, the conclusion may not accurately reflect the actual average age of all the students at the college.
Based on the given information, it can be concluded that the average age of all the students at City College is likely around 20. However, it's important to note that this conclusion is only valid if the sample of 90 students is representative of the entire student population at City College. If the sample is not truly representative, the conclusion may not accurately reflect the actual average age of all the students at the college.
The average age in a sample of 90 students at City College is 20. However, based on this sample alone, it cannot be conclusively determined that the average age of all the students at City College is also 20. This is because the sample may not be fully representative of the entire student population. More information or a larger sample would be needed to make a more accurate conclusion about the average age of all students at City College.
to learn more about the sample click here:
https://brainly.com/question/15659544
#SPJ11
If the sample of 90 students is representative of the entire student population at City College, then we can conclude that the average age of all students is approximately 20 years old.
Based on the given information, the average age in a sample of 90 students at City College is 20.
To determine if this sample can be used to conclude the average age of all students at City College, we need to consider these terms:
Sample:
A subset of a population, which in this case is the group of 90 students at City College.
Population:
The entire group of students at City College that we want to make a conclusion about.
Average (Mean) Age:
The sum of ages divided by the total number of students, in this case, 20 years.
Representativeness:
How well the sample reflects the characteristics of the entire population.
If the sample of 90 students is representative of the entire student population at City College, then we can conclude that the average age of all students is approximately 20 years old.
However, if the sample is not representative, the conclusion may not be accurate.
To make a more accurate conclusion, it is important to ensure that the sample is representative by using a larger sample size or random sampling methods.
For similar question on population.
https://brainly.com/question/30728094
#SPJ11
In the graph below, line k with equation y = -k makes a 45° angle with the x- and y- axes.
Rx: (2, 5)
1. (-2, 5)
2. (-2, -5)
3. (2, -5)
Answers
In the graph, line k with equation y = -k makes a 45° angle with the x- and y- axes. The correct option is 1. (-2, 5).
What is a graph?The angle formed by the line y = - x with the x-axis is 45 degrees, and the angle formed by the y-axis with the positive x-axis is 135 degrees.
The coordinates of the reflected point, when a point (p,q) is reflected over the line y=x, are (q,p)
Moreover, the coordinates of the reflected point, when point (p,q) is reflected over the line y= -x, will be (-q, -p).
Hence, the coordinates of the reflected point when point (2,5) is reflected over the line y= - x will be (-5,-2).
The point (2,5) will change to if it is reflected across the line y=x (5,2).
Therefore, the correct option is 1. (-2, 5).
Learn more about the graph, here:
https://brainly.com/question/7870075
#SPJ1